Pricing of American Options using Simulation Models

Abstract

For the past decades, mathematicians have been able to crack and formulate innovative approaches towards the pricing of various financial derivatives, they still have not figure out the sure and easiest way to correctly price American options. It is still an active field of research within the quantitative finance world.

As compared to European options, there exist no easy way to price American options. Various approaches have been put forward and exist in the literature on how to solve the valuation problem for American options. They each vary from one another. We would be discussing some of them during this thesis such as the optimal stopping formulation, partial differential equations, free boundary formulations.Some are purely numerical in nature and employ finite difference schemes or binomial/trinomial tree methods while others put more emphasis on the analytical work.

Some approaches end up working with integral equations, in which the early exercise boundary features as an unknown. One of the most heavily used techniques is the Longstaff-Schwartz algorithm, which is based on Monte Carlo ideas and which tries to approximate the early exercise boundary by a least squares regression of the continuation value onto a certain set of basic functions.

The aim of this thesis is to compare the different approaches and identify the easiest way that can be used in the valuation of American options. Moreover, we would be discussing what kind of future does financial derivatives (options) have. Although comparing the different approaches with one another would require a certain coverage of numerical data, this thesis would mostly be widely conveyed in a literature format with a few numerical requirements.

Table of Contents

Click to expand Table of Contents

Notations -----------------------------------------------------------------------------------------4

1. Introduction to Financial Derivatives ------------------------------------------------------5
   1. European and American Options-------------------------------------------------5-6
   2. Options Position: Long and short------------------------------------------------ 6-7
   3. Factors affecting Option prices---------------------------------------------------7-9
   4. Put-Call Parity for American Options-------------------------------------------9-10
   5. Bounds on Options ---------------------------------------------------------------10-12
   6. Arbitrage on American Options --------------------------------------------------12
2. Pricing Approaches to American Options ------------------------------------------------13
   1. Numerical Pricing Model
      1. Binomial Model --------------------------------------------------13-15
      2. Trinomial Tree Model--------------------------------------------15-16
      3. Risk-Neutral Valuation------------------------------------------16-17
      4. Monte Carlo-------------------------------------------------------17-18
         1. Feynman-Kac Model------------------------------------18
   2. Black Scholes Equations--------------------------------------------------------18-19
      1. Partial Differential Equations (PDE)------------------------19-20
      2. American Puts--------------------------------------------------20-21
   3. Other Pricing Models
      1. Optimal-stopping formulation-----------------------------------21-23
      2. Free-boundary formulation--------------------------------------23-24
      3. Linear complementarity formulation---------------------------24
      4. Stopping rules and parametric approximations---------------24-26
3. Monte Carlo Simulation---------------------------------------------------------------------26-28
   1. Least Square Monte Carlo Method (LSM)------------------------------------28
   2. Quasi Monte Carlo Methods---------------------------------------------------29-30
4. Comparisons of Pricing Models-----------------------------------------------------------30-31
5. Conclusion -------------------------------------------------------------------------------------31-32
6. References---------------------------------------------------------------------------------------34-36

Notations

• t – time
• T - the expiry (expiration date)
• E - the exercise price of the option
• K - Strike price
• S - market price of the underlying asset; S = S(t)
• V - the value of the option; V = V (S, t)
• C - the value of a call option; C = C (S, t)
• P - the value of a put option; P = P (S, t)
• r - the interest rate
• σ- the volatility of the underlying asset (measure of the standard deviation of the returns of the asset)
• μ- the drift of the underlying asset (measure of the average rate of growth of the asset)
• D- Dividend rate

Chapter 1: Introduction to Financial Derivatives

The success of financial markets depends largely on educated and informed investors who know the risks they are facing and understand the potential for profit but also the probability for loss. It is mostly the financial risk undertaken by financial institutions and individuals that encourages changes in stock market prices, interest rates or exchange rates. Financial instruments for the management of such risk have been developed. They are called financial derivatives. Their values are derived from the price of underlying assets, which could include stocks, bonds, interest rates, foreign currencies and options.

“The modelling of financial derivative products is a fast-growing area of applied mathematics with ‘real-world’ applications to problems originating from the industrial revolution.”

Such instruments were developed to control the spread of risk caused by adverse changes in the market. They also provide the opportunity to make significant profit or loss for those prepared to accept risk. As we will be mainly discussing pricing methods for American options, it is rightly to include this quote from the New Palgrave Dictionary of Economics where Ross (1987) says:

This does not mean, however, that there are no important gaps in the (option pricing) theory. Perhaps of most importance, beyond numerical results…, very little is known about most American options which expire in finite time…Despite such gaps, when judged by its ability to explain the empirical data, option pricing theory is the most successful theory not only in finance, but in all of economics.

The structure of this dissertation will be split into different chapters.

In Chapter 1, we would give a brief introduction on Options and find out about the factors that affect them. We would also look into the various positions and types of options mainly focusing on American options.

Chapter 2 would then introduce us to the various pricing approaches and their validity to the modern trading structure while again emphasising on American options.

In Chapter 3, we would further discuss the Monte Carlo Simulation, its properties as well as drawbacks.

Chapter 4 will provide us with some insight concerning numerical solutions for American puts.

Finally, in Chapter 5, we would attempt to compare and differentiate between the different approaches.

We would then conclude this thesis by summarising what we have achieved throughout our research and give a final verdict on pricing American options.

1.1 Options Contract: European and American

An option is a financial contract between two parties; the buyer (also known as the holder) and the seller (also known as the writer). An option gives its holder the right, but not the obligation, to buy or sell an underlying asset at a fixed price in the present. More precisely, A call option gives its holder the right to buy an underlying asset by a maturity date at a fixed price.

A put option gives its holder the right to sell the underlying asset by a maturity date at a fixed price. If the price of the underlying asset moves in such a way that the price agreed by the option becomes unappealing, then the holder of the option may simply choose to disregard it. Options provide protection against negative movements while preserving the ability to gain from profitable price movements. However, these benefits of option contracts, relative to the other derivatives, must be paid for in the beginning in the form of an option premium.

The Options contract can be further expanded into two categories: European and American. It is a distinction which has nothing to do with the geography of the world. A European call option is one which at a prescribed time in the future (the expiry date) the holder of the option may purchase the underlying asset, for a fixed amount (the strike price). Likewise, a holder can exercise a European put option to sell an underlying asset for a future price at a fixed time. Such an option is usually termed as a ‘standard derivative’.

American options can be exercised at any time up to the expiry date, whereas European options can only be exercised on the expiry date itself. Apart from the traditional European and American options, other options have also been developed known as the exotic options.

Since the early 1980’s, banks and other financial institutions have been creative in designing non-standard derivatives to meet the needs of clients. Such an example is the non-standard American option in which early exercise is restricted to certain dates known as the Bermudan option. As a matter of fact, the Bermudan option is the combination of both the European and American option.

The Bermudan option can be exercised on the maturity date and any specified dates between the day of purchase and the maturity date. Other than the Bermudan options, we also have the Asian options whose payoff is determined by the average underlying price of an asset over a pre-determined time rather than on the maturity date. It also known as the Average option.

One would expect to make significant return from their trading which is not always the case. Since the option confers on its holder a right with no obligation it has some value. This must be paid for at the time of opening the trade. Conversely, the writer of the option must be compensated for the obligation he has undertaken. The questions to be asked here are:

1. What should be the correct price of this option? i.e., what amount of premium would the writer be ready to pay?
2. Will the writer be willing to undertake the risk associated with his obligation?

1.2 Options Position: Long and Short

There are two sides to every option contract. On one side is the holder who has taken a long position (i.e., has bought the option) while on the other side is the writer who has taken a short position (i.e., has sold the option). There are four types of option positions:

1. A long position in a call option.

A long call signifies that the holder owns the underlying asset. On the other hand, when an investor buys a call option, he does not own the underlying asset.

2. A short position in a call option.

A short call means the sale of a call option that gives the holder the right, but not the obligation, to buy an option at a given price.

3. A long position in a put option.

The long put is one where the investor buy put options hoping that the price of the underlying asset will go significantly below the strike price before the expiration date.

4. A short position in a put option.

A short put happens when if an investor writes a put option, then the latter is in the obligation to buy the shares of the underlying stock if the put option holder exercises the option, or if the option expires.

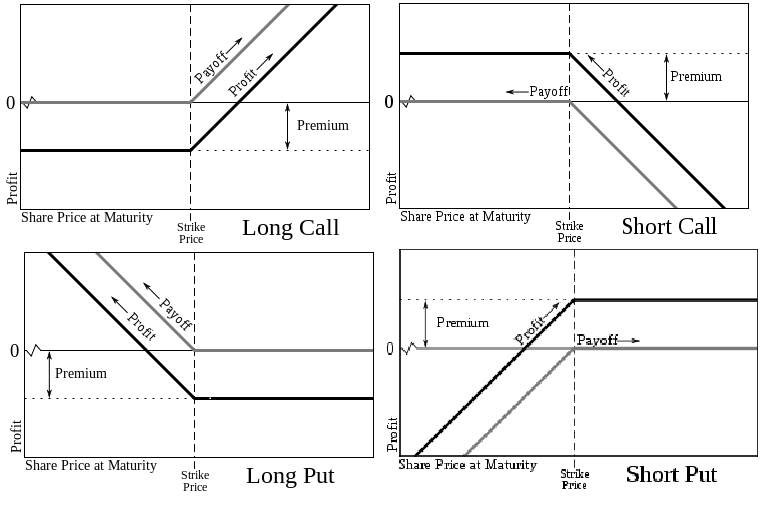
Figure1

1.3 Factors affecting option prices

Speculative traders make money while taking advantage in the options markets by using options as tools to exploit views about economic factors. In order to successfully manage the options, we need to have a minimum knowledge about the factors affecting the options such as:

Factors affecting Option Prices	Notation
Price of underlying asset/stock	S
Strike price of the option	K
Time to Maturity	T-t
Volatility	σ
Riskless interest rate	R
Present value of dividends from t-T	D

Table1 In the above table, the risk-free interest rate is the theoretical rate of return on a risk-free investment while the volatility represents how the price varies over time. Each of these factors affect the European and American options differently as shown in the table below:

Options	European		American
Variable	Call	Put	Call	Put
Stock Price	+	-	+	-
Strike Price	-	+	-	+
Time to maturity	?	?	+	+
Volatility	+	+	+	+
Riskless Interest rate	+	-	+	-
Dividends	-	+	-	+

Table2

In the above table the symbols. ‘+’ signifies that the factor increases the price of the option, ‘-’ signifies that the factor decreases the price of the option and ‘?’ states that the relationship between the two fluctuates.

The way each factor affects each type of options is natural. For example, if price goes up, the price of a call goes up resulting in greater increases in the price of the stock and the price of a put would go down as the decrease will not be as fast as the increase. This is due to the fact that, the path the stock takes is the original price multiplied by some variables. Hence increases tend to happen faster than decreases. As interest rates increase, investors would expect more return from the option. However due to the fact that inflation and interest rates are closely related, the value any money earn in the future would have a decreased value. This would increase the price of stocks slightly which would result in high paying off for calls and low paying offs for puts.

As for dividends, when the date at which claim to dividends changes, the stock price decreases. This in turn makes the price of calls to decrease and the price of puts to increase. The most unusual factors however are the time to maturity and volatility. The time to maturity for American options increases for both puts and calls. For example, if we have two American options, and if the only difference is that one has a longer time to expiration than the other, then the owner of the option with a longer time has all of the same opportunities to exercise it which in turn increases the value of the option. However, for European options, this is not the case.

Finally, volatility is a measure of how uncertain we are of the stocks future price. If volatility increases, the chance the stock will do very well or very poorly increases. As our maximum loss from an option contract is the price but the profit is either infinite or large this benefits the owner hugely Other than the factors mentioned above, there are other economic factors as well that affect the option prices such as financial managers resigning over accounting frauds, or stiff competition from competitors, or even fear of wars. There are also indirect factors that are less likely to affect the value of the option, but may affect the price of the option you pay. These include low liquidity during pre-holiday periods that results in wider bid-ask spreads, or lack of depth that means the direction of the option moves prices against you.

1.4 Put-Call parity on American options

Put-call parity is a principle that states the relationship between the price of put and call options of the same underlying asset, along with the strike price and expiration date. Put-call parity states that for example, if we hold simultaneously a short European put with a long European call of the underlying asset, then we will get the same return as holding one forward contract on the same underlying asset, with the same expiration date and a forward price equal to the option's strike price.

If the prices of the put and call options deviate from each other this relationship does not hold which would then make an arbitrage opportunity to come up, which means that experienced traders can theoretically earn risk-free profit. Such opportunities are however unusual and have a short life in liquid markets. While a put-call parity is always present in European Options, it might not be the case with American Options. An American call option is an option which buys a specified number of shares that may be exercised at any time before or on the option’s expiry date T .

The exercise policy of the option holder is necessarily based on the information accumulated to date and not on the future prices of the stock. American put-call parity is a pair of inequalities for the same strike price options of the same maturity as shown in equations below: P+S-D≤C+X (1.1) C+Xe-r(T-t)≤P+S (1.2), where P stands for Put options and C for call options. If equation 1.1 does not hold, then P+S-D>C+X . In other words, P+S>D+C+X . Therefore, in order to generate an arbitrage profit, one would need to short the put and the stock and use more resources to buy the call, invest in the strike, and invest in the present value of the dividends D.

If equation 1.2 does not hold, then C+Xe-r(T-t)>P+S . In such a situation, we would sell the call, borrow the present value (PV) of the strike, buy the put and the stock, and reduce the surplus. Per se, we cannot derive an equality for the American put-call parity as half of the arbitrage argument would break down. For example, if the call option ‘C’ is very high as compared to the put option ‘P’ in (1.1), then we cannot generate an arbitrage by shorting the call, borrowing the strike, borrowing the present value of the dividend, and using the proceeds to buy the put and the stock.

The reason is that if we are assigned an exercise on the short call, although we have the stock to deliver, the receipt of the strike combined with liquidation of the put will not necessarily cover your borrowing. A similar argument would apply to equation 1.2. Let’s assume that the equation holds with strict inequality and we short the put and stock, using the proceeds to buy a call plus invest the present value of the strike. If we are assigned an exercise on the short put, then the receipt of the stock can be used to cover your short stock, but the present value of the strike together with the liquidation value of the call will not necessarily suffice to pay the strike. Furthermore, we would not be able to pay the dividends on the short stock in the interim.

1.5 Bounds on Option Prices

According to the arbitrage theory the option holder has to pay the option writer for his right: the amount he has to pay would be the option price. Arbitrage theory assumes that there is no opportunity to make a sure profit without any risk otherwise the opportunity would disappear the moment it rose.

Firstly, let’s consider the call options, nevertheless arbitrage considerations provide bounds for put options. The bounds described here are purely based on the ‘no arbitrage’ assumption. Assume CE is the price of a European call option and CA the price of an American call option. The first bound is that a call option cannot be worth less than zero. In other words, having the right but not the obligation to do something can either be zero or a positive amount. That is, CE ≥ 0 and CA≥ 0 The next bound is that the call price cannot exceed the asset price. That is, CE ≤ St and CA ≤ St This is because the right to buy an asset cannot be worth more than the asset itself at any time. After all, if the right is exercised, it just gives the asset and no more.

“If this relationship was not true, then an arbitrageur could make a risk-less profit by buying the underlying asset and selling the call option.”

There is a lower bound for the price of a European call option which is derived by considering two alternative investment strategies:

1. Buy a share today at a price St, or
2. Buy a European call option on the share at a price of CEtoday and, at the same time, deposit enough money at the risk-free interest rate to yield the exercise cost Kat time T. The sum to deposit now is the present value of K, PV(K)which is known from the payoff equation: PV(K)=Ke-r(T-t).

At time T the first portfolio will be worth ST and the second will be worth: max (ST, K) If ST>K , the call option is exercised at maturity then the portfolio would be worth ST On the other hand if ST (1.3) The worst that can happen to an option is that it expires worthless, hence its value cannot be negative. This gives the following equation, CE ≥ max(St-PV(K), 0) (1.4)

Similarly, put options have the following price bounds PE≥0 and PA≥0 (1.5) PE≤K and PA≤K (1.6) where PE is the value of a European put option and PA is the value of an American put option, respectively. The bounds imply that a put cannot have a negative value (1.5), and the price of a put cannot exceed the exercise price (1.6). Similar to the call equation (1.3), a European put option has a lower bound given as PE≥PV K-St (1.7)

Also, similar to (1.4), the following holds: PE≥ max(PV(K)-St,0) (1.8)

In the case of early exercise, CA ≥ CE PA≥PE since American options provide more exercise opportunities than the corresponding European options. It follows from (1.4) and (1.8) that CE≥St-PV(K) PE≥PV (K)–St Given r>0 , it follows that CE>St-K . It is thus never best to exercise an American call option on a non-dividend-paying stock before the expiry date. (If it was best to exercise early, CE would be equal St-K ). However, it may be optimal to exercise an American put option on a non-dividend-paying stock early. At any given time during a contract, a put option should always be exercised early if it is sufficiently deeply in the money. For an American put option, the stronger condition PE≥ K-St must always hold since immediate exercise is always possible.

In general, the early exercise of a put option becomes more attractive as St decreases, as r increases and as the volatility decreases. If a put-call parity doesn’t hold up, then this gives rise to arbitrage opportunities.

1.6 Arbitrage on American Options

The right to exercise an American option before its expiration date implies that the value of the latter should never go below its initial value. For example, if the spot price if St and strike price is K , then the value of the option should not go below maxK-St,0 for American put or max(St-K,0) for American call.

Let Cta denote the arbitrage price at time t of an American call option written on one share of a stock. At Cta , t ≤ T , so that the market for the American calls stay arbitrage free. The first goal is to show that the price of an American call option in the CRR arbitrage-free market model coincides with the arbitrage price of a European call option with the same expiry date and strike price.

For this purpose, it is sufficient to show that the American call option should never be exercised before maturity, since otherwise the option writer would be able to make risk-free profit. It is worth noting that, by convention, when an American call is exercised at time t, its payoff equals (St-K)+ , rather than St-K . Due to this convention, we may assume that an American call or put option should be exercised by its holder either prior to or at maturity date.

Chapter 2: Pricing Approaches to American Options

There have been many approaches put forward in order to price financial derivatives. While it is easy to price European Options, it is not the case for American options due to its ability to exercise any time before and on the maturity date. In this chapter, we will be reviewing the various pricing approaches put forward. While some of these approaches are purely numerical in nature, others are more or less analytical.

2.1 Numerical Pricing Methods

2.1.1. Binomial option pricing

Simple yet powerful, such is the binomial option pricing method which is used to solve a lot of complex option pricing problems. It was first introduced in 1979 by John C. Cox, Stephen Ross and Mark E. Rubinstein. As such the binomial option pricing method is often denoted as the CRR model. The plus point about this model is that it covers an underlying asset over a period of time rather than just a point. Because of this, this model mostly useful to American options. Also, this method also takes into account the effects of dividends paid during the life of an option. It uses an iterative procedure, allowing for the specification of nodes, or points in time, during the time period between the valuation date and the option's expiry date. The model reduces possibilities of price changes as well as removes the possibility for arbitrage.

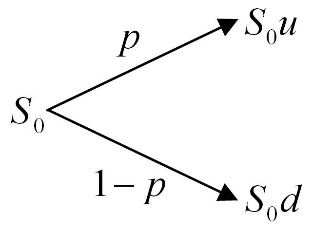
Fig 2.1: Two-step binomial model with period 1

The binomial tree consists of N time steps corresponding to times k=0, 1, . . . , N , and models an asset price Sk . The price is normalized to S0=1 . Every outgoing branch in the tree has the price either moving up to Sk+1=uSk or down to Sk+1=dSk where u=eσt and d=e-σt=1u, where u>1

If we define the ‘up’ probability p (the same at every node) then Sk is a discrete-time stochastic process. We let Fk be the σ -field generated by {S0,S1,…,Sk} . At time k the possible price values are specified by Sk=Sk0,…, Sk[k] with Sjj=ukd2j=d2j-k (2.1) (as such Sk0=uk, Skk=dk , as such the prices are listed in a decreasing order) For instance, there is a riskless savings account with £1 invested at time k and is worth £ R at time k+1 . The condition for no arbitrage is as such: d

1. That there is a perfectly efficient market due to which it is able to provide a mathematical solution for an option at each point in the time frame specified.
2. That the spot price can only go in two direction hence the name binomial at each node and that there can be only two possible prices (up and down).
3. That the underlying asset does not pay any dividends at any point.
4. That the rate of interest ( r) is constant throughout the life of the option.
5. That there are no taxes and no transaction cost in motion on the market.
6. That the risk factor is not really problem for the investors.

The model takes a risk-neutral approach to valuation and assumes that underlying prices can only either increase or decrease with time until the option expires without any value. Like all methods, the binomial pricing option has its advantages and disadvantages. One of its main advantages is that it is very easy and simple to use. It is much useful when pricing American options as well as Bermudan options which are partly made of American option as both have the ability to be exercised before their maturity date. However, the model can become quite complicated if the time period is more than one. In other words, it would become difficult to price an option in a multi period binomial model. It can become quite time consuming as well in a multi period binomial model.

2.1.2 Trinomial Tree Model

The trinomial model was in turn developed by P. Boyle in 1986 as an extension to the binomial pricing option. It basically uses a lattice based computational model in order to price options. The model incorporates three possible values that an underlying asset can have in one time period. The three possible values the underlying asset can have in a time period may be greater than, the same as, or less than the current value. The trinomial model is a less complicated but numerically a more effective method to price American options.

The trinomial model follows the same approach as the binomial model where the price at each node can be determined; tj=j∆t, j=0,…., n can change to three instead of two directions with ∆t=Tn . Each value at the end of the node can be found by multiplying the current factor with the corresponding factor u , d or m where u=eσ2∆t , d=e-σ2∆t=1u and m=1 As such each branch has its corresponding probabilities; pu=e(r-q)∆t/2-e-σ2∆teσ2∆t-e-σ2∆t2, pd=eσ2∆t-e(r-q)∆t/2eσ2∆t-e-σ2∆t2, pm=1-(pu-pd) In the above equation, ∆t is the time to maturity divided by the number of time steps; r is the riskless interest rate; σ is the corresponding volatility of the underlying asset and q is the corresponding dividend yield.

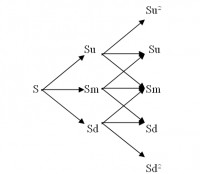
Fig 2.2: Trinomial Tree Model

The trinomial option pricing model differentiates itself from the binomial option pricing model in one key aspect. It incorporates another possible value in one periods time. Under the binomial option pricing model, it is assumed that the value of the underlying asset will either be greater than or less than its current value. The trinomial model, on the other hand, incorporates a third possible value, which incorporates a zero change in value over a time period. The trinomial model is also related to the classical procedures for solving partial differential equations, which are also used to solve the Black-Scholes differential equations. This assumption makes the trinomial model a bit more relevant to a real-life situation where it is possible that the value of an underlying asset will not change or a certain period of time, like month or a year.

2.1.3 Risk-Neutral Valuation (simulation)

Let us consider an equity price process S(t) that follows a Geometric Brownian motion process according to the following stochastic differential equation: dS=μSdt+σSdX (2.4)

In the above equation, μ is the measure of the average rate of growth of the underlying asset price which is also known as the drift and σ is the volatility of the asset, which measures the standard deviation of the returns while X=X(t) is the Brownian motion. Both the drift and the volatility are considered to be constant. The option payout function is u(S,t) . A path dependent option is one for which u(S,t) depends on the entire path {S(t):0(2.5) In the above equation, E' is the risk-neutral expectation, for which the growth rate μ in (2.4) is replaced by r.

The maximum is taken all over all stopping times τ with t<τAs such, there are several Monte Carlo simulation models are known and used in practice. The Monte Carlo technique for valuing derivatives is mainly based on the probability distribution of complete histories of the underlying derivative. The difficulty that occurs when pricing American options through Monte Carlo valuation is that Monte Carlo requires options that depend on multiple underlying derivatives or those that involve path dependent features. Since the determination of the optimal exercise time depends on an average over future events, Monte Carlo simulation for an American option has a “Monte Carlo on Monte Carlo” feature that makes it computationally very complex.

For a Monte-Carlo simulation of an American option, one performs the same type of Monte-Carlo simulation as for European options but then takes the Sup for all times τ ∈ [t, T] to obtain a realization of Pt . Then by doing this N times and taking the average, one obtains Pt for one value of S . In practice this is quite expensive and one may prefer binomial trees (see above) or finite difference or finite element methods A disadvantage of this method is that suitable accuracy may require a very large number of simulation trials. In general, the expected error decreases with the number of trials n by factor 1/n ; so, one more digit of accuracy requires 100 times as many trials. Often tens of thousands of trials are required to obtain two-place accuracy.

2.1.4.1 The Feynman-Kac Theorem

Named after Richard Feynman and Mark Kac, this theorem establishes a possible relationship between solutions of parabolic partial differential equations (PDEs) to an expectation which establishes a mathematical link between PDE formulation of the diffusion complications in finance and the Monte Carlo simulations. Given the stochastic processes: dXi=bidt+∑j=1naijdWj

For i =1…n , With formal solution XiT=Xit+∫tTbidt+∫tT∑j=1naijdWj , Any function V(t,X) with boundary conditions VT,X=f(X) That satisfies the partial differential equation ∂V∂t+g+12∑i,j=1ncij∂2V∂Xi∂Xj+∑i=1nbi∂V∂XI=kV with cij∶= ∑k=1naikajk Can be represented as the expectation Vt,X=E[fXTe-∫tTkdu+∫tTge-∫tskduds Hereby, all the coefficients aij, bi, k and g can be functions both of time t and the state vector X(t) .

2.2 Black-Scholes equation [Analytical]

The Black-Scholes formula (also known as the Black-Scholes-Merton) was the first and most popular used model for option pricing. It is mainly used to calculate the theoretical value of European-style options using current stock prices, expected dividends, the option's strike price, expected interest rates, time to expiration and expected volatility. The formula was formerly developed by three economists namely; Fischer Black, Myron Scholes and Robert Merton and was first introduced in their 1973 paper, "The Pricing of Options and Corporate Liabilities" published in the Journal of Political Economy. The Black-Scholes model makes the following assumptions:

• Only European options can be exercised at expiration
• During the life span of the option, no dividends is paid out.
• The need for efficient markets (i.e., market movements cannot be predicted)
• There are no transaction costs in buying the option
• The risk-free rate and volatility of the underlying are known and constant
• The returns on the underlying assets are normally distributed

“The key to the Black-Scholes analysis is the observation that there exists a dynamic portfolio trading strategy in the underlying asset which replicates the returns from an option on that asset.” Thus, to avoid the possibility of arbitrage, the value of the option must always be equal to the value of the replicating portfolio. This leads to a linear parabolic PDE for which an analytic solution exists. The replicating-portfolio approach of Black & Scholes can be generalised and applied to the pricing of general financial derivatives, contingent upon several underlying cash securities and other variables, with arbitrary payoffs. The multidimensional equations which these multi-factor models imply do not, in general, have readily available analytic solutions and so numerical methods have to be applied. In addition, financial derivatives which permit early exercise do not have analytic solutions and numerical algorithms have to be employed to approximate the solutions to these problems.

2.2.1 Partial differential equation

The one-dimensional PDE for the pricing of one-dimensional options is derived using the Black-Scholes approach. The Black-Scholes analysis, which leads to the value of an option makes some additional assumptions.

1. The underlying asset price follows the lognormal random walk: dSt=μSt+σStdWt.
2. The price of the option uis a continuous, differentiable function of the asset price Stand time t. i.e., u ≡ u(St, t).
3. The risk-less rate of interest is a known function of time during the life of the option, investors can borrow and lend at this rate.
4. The underlying asset pays no dividends during the life of the option.

A portfolio is constructed with the initial value ∏0 and value at time t , ∏t , which consists of one option and a number -Δt , delta (as yet unspecified) of the security St . The value of the portfolio at time t is given by Πt= u(St, t)-ΔtSt (2.6). The change in the value of the portfolio in time [0, t] is therefore ∏t-∏0= ∫0tduSτ,τ-∫0t∆τdSτ Note that Δt has not changed during the time-step. Ito’s lemma implies that the portfolio follows the random walk: d∏t=∂u∂tdt+∂u∂SdSt+12σ2St2∂2u∂S2dt-∆tdSt

2.2.2 American Put Option

The American put option gives the owner the right to sell the underlying asset at a fixed strike price K∈R+ at any time before the expiry date of the option T>0 . Let’s assume that the spot price of the American put is St and strike price K and time expiration T . If the spot price is St* at time t* is 0, then St=0 holds for t≥t* since the price process follows a geometric Brownian motion. At this point, it is not recommended to exercise the option at a later date. If St*=0 , then the value of the put at t* is K , i.e. the initial value.

The no-arbitrage condition demands that the price of the option is never less than the payoff value, g(S)=max(K-S, 0) . This condition leads to a partial differential inequality equation satisfied by the value of the American. To derive this, a riskless portfolio is constructed. The possibility of early exercise demands that the appreciation in the value of the portfolio is bounded above by the risk-free rate of interest. The pricing function u satisfies the inequality: -∂u∂t≥LBSu In Ω={S: S≥0} × [0, T] where LBS is the Black-Scholes differential operator of equation: -∂u∂t=12σ2S2∂2u∂S2+rS∂u∂S-ru=LBS u .

The valuation of American options is a free boundary problem. Typically, at each time t there is a value of the spot which marks the boundary between two regions; to one side one should hold the option and to the other side one should exercise it. That is, the domain Ω is demarcated into two regions C and ℇ where C={(S, t)∈Ω:u(S, t)>g(S)} , is the continuation or holding region. Its complement is given by ℇ={(S, t)∈Ω:u(S, t)=g(S)} Which is the exercise region. If the option is exercised, then its value is determined by the payoff. If it is held then its value must be greater than the immediate payoff. Since the option is either exercised or held, the pricing function satisfies the linear complementarity problem given by, -∂uS,t∂t≥LBSuS,t∈R+×[o,T] uS,t≥gS∀S,t∈R+×[o,T] -∂u∂t-LBSu.u-g=0∀(S,t) ∈R+×[o,T] and final condition u(S, T)=g(S) .

The complementarity formulation can be generalised to multi-factor financial derivatives. While it initially came into existence in 1973, the Black-Scholes formula was initially devised to price European options on stocks that do not pay any dividends. The main advantage of the Black-Scholes is that it allows one to calculate large amount of option prices in a very short time. Its major disadvantage however comes when pricing the American options. Black-Scholes cannot accurately price American option as the formula can only calculate the option at the expirations time. It ignores all possibility of an early exercise of the American option. However, a loophole can be found in the case of American calls where the American call is worth the same as a European call making it unsuitable for exercising it early.

2.3. Other Pricing Models

2.3.1 Optimal-stopping formulation

In mathematical theory, optional stopping is one where the problem arises when choosing the time to exercise an option in order to maximise profits or minimize loss. Due to the fact that the American option can be exercised on or before its maturity date sort of makes it an optimal-stopping problem. Following a classic set up under the Black-Scholes.

The stock price would normally follow a geometric Brownian motion: St=S0exp⁡r-δ-σ22t+σBt {\displaystyle r}{\displaystyle S_{t}=S_{0}\exp \left\{\left(r-\delta -{\frac {\sigma ^{2}}{2}}\right)t+\sigma B_{t}\right\}} Let us find the fair value of an American option (Vam) contract which is equivalent to solving the following optimal-stopping-time problem Vam=supt∈T E[e-∫0τruduPτSτ] (2.1)

In the above equation, the expectation is taken under the risk-neutral martingale measure. The instantaneous short rate process r(t) is used to discount the payoff Pτ at time τ , and the supremum in (2.1) is taken over all admissible stopping times τ ∈ T between now and the final expiry of the option. The rate r is constant. Let us consider the case of an American put option with strike price K on a single underlying S with price process St . Assuming that the process follows a geometric Brownian motion with interest rate r under the risk-neutral martingale measure, the equation 2.1 can be further converted into the following; supτ∈T E[e-τrmaxK-Sτ,0] (2.2) In case of a put option on a single underlying the hold and exercise regions are half planes divided by the optimal exercise boundary B*(t) and the supremum in (2.2) is attained for an optimal stopping time τ* of the form τ*=inft≥0:St≤B*t (2.3) Figure 2.1 illustrates the situation for a sample path which hits the optimal exercise boundary.

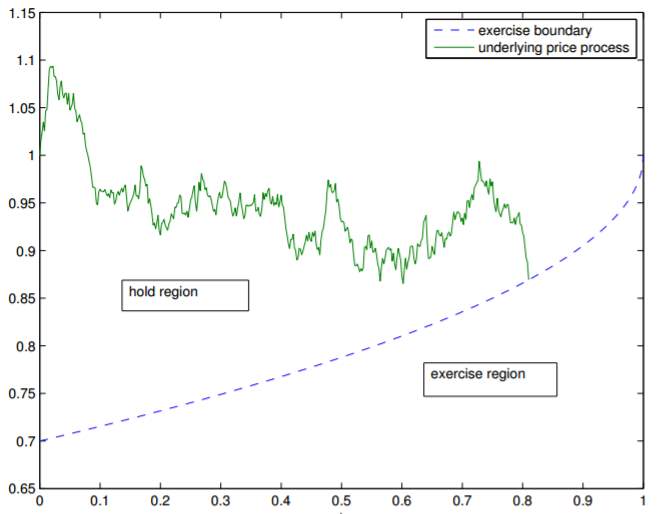
Fig 2.1: hold and exercise region under a given exercise rule

The difference in value between an American derivative and its European equivalent is referred to as the early exercise premium. In contrast to European options there are generally no closed-form solutions for American option even for plain vanilla instruments. The pricing of an American option is based on the assumption that a rational option holder will choose to exercise his right optimally in some sense. Thus, finding an optimal exercise strategy is at the core of pricing an American option. Mathematically, this translates into the optimal stopping formulation.

2.3.2 Free-boundary formulation

Another plausible method on how we can possibly price the American options is the free boundary problem. Let us consider the case of American put option. The decision to whether exercise an option or to hold it for a little further depends naturally on the current of the underlying asset basically at every point in time. Mathematically, the (t, S) plane can be divided into a hold region (where it is optimal to hold the option) and an exercise region (where it is optimal to exercise it). The barrier between those two regions is called the optimal exercise boundary B*(t) (the blue line).

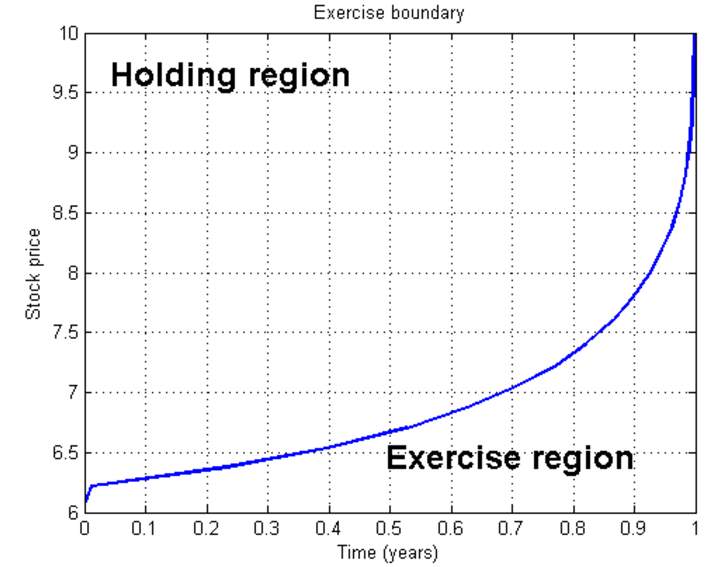
Fig2.3: (t, S) plane showing the hold and exercise region.

Let the fair value of the American put option be Pam . In this situation, the hold region lies above the exercise boundary B*(t) in the (t, S) plane. Within the hold region the value function Pam satisfies the Black-Scholes equation, i.e. LBSPam∶=∂Pam∂t+12σ2S2∂2Pam∂S2+rS∂Pam∂S-rPam=0 (2.4) where r and σ are the usual drift and volatility parameters from the geometric Brownian motion SDE.

At expiry T and along the optimal exercise boundary B*(t) the option is worth its payoff, i.e. Pam(T, S)=max (K-S, 0) and Pam(t, B*(t))=max (K-B*(t), 0). The transition between the two regions is smooth, in the sense of the so-called smooth pasting condition ∂Pam∂S t,B*t=-1 One of the drawbacks of the optimal exercise boundary is that the boundary is not known but must in fact be computed as part of the solution, making the problem is much harder to solve than a simple boundary value problem. We note that the smooth pasting condition only holds for options whose payoff is sufficiently smooth. It does not hold in the case of an American digital put for example. Another point worth mentioning is that for more complicated American derivatives the hold region might not be simply connected at all times. Overall, free boundary problems are hard to solve numerically.

2.3.3 Linear complementarity formulation

Another way to characterize the price of an American option is as the solution of a linear complementarity formulation. In this formulation, we are looking for a function V (S, t) such that LBSV≤0, VS,t≥P(S,t) VS,t-PS,tLBSV=0 And VS,T=P(S,T) Here, P(S, t) denotes the payoff function of the option and the Black-Scholes operator LBS is defined as in (2.4).

The linear complementarity formulation is the clever combination of several features of an American option. Some of these can easily be argued heuristically. We had already argued before that based on the no-arbitrage assumption the option must be worth no less than its immediate payoff, i.e. V(S, t)≥P(S, t). Moreover, it is clear that the option value coincides with its payoff value whenever it is optimal to exercise. It can be shown that within the hold region of the option its price function V(S,t) satisfies the Black Scholes equation. Combining these observations one ends up with the linear complementarity formulation above.

2.3.3 Stopping rules and parametric approximations

The connection in (2.3) allows us to interchangeably formulate the pricing problem either in terms of stopping times or in terms of exercise regions. Note that any choice of a stopping time τ̂∈T will produce a (usually suboptimal) value in the expectation from (2.1), i.e. Vam(τ̂)=Ee-τ̂rPτ̂Sτ̂≤Vam (2.5) If the optimal exercise region ε* is known, then the optimal stopping time τ* is the first time that St enters the exercise region τ*=infτ∈T{t≥0:St∈ε* } (2.6) and the fair value of the option can be computed as a simple expected value according to Vam(τ*)=Ee-τ*rPτ*Sτ*=Vam (2.7)

The mapping implicit in (2.6) can be used to assign a stopping time to any given “exercise region”. As such there is a possibility in terms of optimizing over exercise regions (or boundaries) and find the value of an American option. The interesting consequence is that given an exercise strategy (i.e. an exercise region), a forward Monte Carlo simulation of the underlying path process can be used, compute the payoff for each path and take an average to find the value of the option under the chosen exercise strategy.

The emphasis here is that most numerical pricing algorithms for American options including the famous Longstaff- Schwartz algorithm are based on backward iterations and that forward algorithms are usually unsuited for the problem. Suppose now that we can parametrize all feasible exercise regions εθ by some parameter θ ∈ Θ and denote by τ(θ) the stopping time associated with εθ according to the mapping presented in (2.6). The option value is then approximately equal to Ṽam=Supθ∈ΘE[e-τθrPτθSτθ] (2.8) however, the value computed in (2.8) is in general biased low because we might not hit all feasible stopping times in our approximation.

In other words, the set τ(Θ)⊂T will in general be a proper subset of T and hence Ṽam=Supθ∈ΘEe-τθrPτθSτθ≤Supτ∈TE[e-τrPτSτ=Vam Nonetheless, equation (2.8) is the fundamental base of our numerical approach. For an American put option a lot is known about the optimal exercise boundary. One of its main characteristics is its asymptotic behaviour close to the expiry date of the option, where it clearly hits the strike. In fact, the optimal exercise boundary of an American put option asymptotically approaches its strike level K displaying a square root i.e. B*t~K-cT-t for T-t≪1 (2.9) with an appropriate constant c .

Even more importantly, it influences our choice of a parametric family of feasible exercise boundaries, which we use in the optimization problem (2.8).

Chapter 3: The Monte Carlo Simulation (MC)

The Monte Carlo method is well suited once it is agreed that security pricing can be represented by expectations. Monte Carlo seeks to solve the pricing equation satisfied by the price differential equation by representing the solution as an expectation, then using numerical simulation to evaluate the expectation. The approach consists of the following steps:

• Sample paths of the underlying state variables (underlying asset prices and interest rates) are simulated over the relevant time frame.
• The discounted cash flows of a security on each sample path, as determined by the structure of the security, is evaluated. Let’s call it uj.
• The discounted cash flows are averaged over the sample paths. That is, û=1N∑j=1Nuj is computed.
• The standard deviation of the simulation is computed, σû̂=1N-1∑j=1N(uj-û)2

As a simple example, refer to Equation (2.15). Assume stock price evolves according to dStSt=r dt+σ dWt By Ito’s calculus, St=S0er-σ22t+σWt So, the sample path could be generated by St+∆t=Ster-σ22∆t+σ∆tZ where Z is N (0, 1). Monte Carlo methods compute a multi-dimensional integral, the expected value of the discounted payoffs over the space of sample paths.

The increasing difficulties in pricing derivatives securities have led to the need to develop further high dimensional integrals. Monte Carlo methods are usually very flexible and easy to implement. They can readily accommodate most forms of path-dependent options, and underlying factors can be allowed to evolve according to complex stochastic systems. Also, the computational complexity is linear in the number of state variables (unlike finite difference methods, or lattice models), and so the method is well suited to very high dimensional problems.

There are, however, difficulties in applying these methods to early-exercise options. Standard simulation programs are forward algorithms; however, pricing American-style options generally requires a backward algorithm. The Monte Carlo simulation is a substitute to the numerical PDE method. Boyle (1977) was the first one to bring the Monte Carlo simulation into finance.

Monte Carlo simulation is the primary and most suited method for pricing complex financial derivatives, such as contracts whose payoff depends on several correlated assets or on the entire sample path of an asset price. We can simulate as many sample paths as desired according to the underlying stochastic differential equation that describes the stock process. For each sample path, the option value is determined and the average from all paths is the estimated option price. The option price μ is written as an integral that represents the mathematical expectation of the discounted payoff under a so-called risk-neutral probability measure. This expectation is usually with respect to a non-uniform density over the real space, but with a change of variables, it can be rewritten as an integral over the s-dimensional unit hypercube: 0,1)t=u=u0,…, ut-1:0 the final stock price if one assumes a given starting point, time, constant interest rate and volatility.

It is much easier to see that the Monte Carlo simulation would work in a forward direction. However, for the American option, it might not be the case. Because of early exercise condition, in contrast to a partial differential equation, we would also need to know the option value at the in-between times between the simulation start time and the option expiry time. In Monte-Carlo this information is harder to obtain, therefore, even though it is simple and capable of handling multi-factor problems, we would need to solve the problem by going backwards.

As such the Monte Carlo simulation becomes difficult to implement. Like all the methods described above, the Monte Carlo simulation also comes with its advantages and disadvantages. To begin with, the probability distributions within the model can be easily implemented without the need to approximate them. Furthermore, the correlations of the model can be modelled with ease. The method itself is quite easy to implement. Moreover, the simulation can be easily mounted on various software packages such as Matlab and Excel. The main drawback of this simulation however is that it is more of an approximate way to price options than a sure way although it is possible to reduce the percentage of deviation by simply increasing the number of simulations. That said, this set new limitations to the model such as how much time will take for an analyst to generate the simulations.

3.1 Least Square Monte Carlo method (LSM)

In 2001, Longstaff and Schwartz introduced the Monte Carlo simulation and least squares algorithm of Carriere in order to price American options. Option holders would compare the payoff between immediate exercise and exercise it at a later date (continuation date) depending on which one is higher. Else, the options would remain as it is. The expected payoff for a later exercise is conditional on the information available at that time point.

The main emphasis for this approach is that the conditional expectation can be estimated from the cross-sectional information in the simulation by using least squares. This makes this approach readily applicable in path-dependent and multifactor situations where traditional finite difference techniques cannot be used. In order to find out the conditional expectation function, we revert back the realized payoffs from continuation on a set of basic functions in the underlying asset prices.

The fitted values are chosen as the expected continuation values. We would compare these continuation values with the immediate exercise values and make the optimal exercise decisions. We would then obtain a complete specification of the optimal exercise strategy along each path. We can use this algorithm and discount the optimal payoffs to time zero. That would give the option price.

The method starts with N random paths (Skn, tn) for 1≤k≤N and tn=ndt . Valuation is performed by rolling-back on these paths. Suppose that Fn+1k=FSkn+1, tn+1 is known. For points Stn, tn set X= Skn the current equity value and Y=e-rdtF(Skn+1,tn+1) the value of deferred exercise. Then perform regression of Y as a function of the polynomials X,X2,…, Xm for some small value of m which is called basic function; i.e. approximate Yk by a least squares fit of these polynomials in X .

Hence we use this regressed value in deciding whether to exercise early.

3.2 Quasi-Monte Carlo Methods-QMC (low-discrepancy)

Instead of generating sample paths randomly, it is possible to systematically select points in a probability spaces so as to optimally "fill up" the space. The selection of points is a low-discrepancy sequence. Taking averages of derivative payoffs at points in a low-discrepancy sequence is often more efficient than taking averages of payoffs at random points. Because of the multidimensional numerical integration problem, the quasi-Monte Carlo methods was proposed in lieu of the Monte Carlo methods. In order to resolve this problem, we would construct the following equation: μ=∫[0,1)tf(u)du where f is a square-integral function.

To approximate μ , both MC and QMC proceed by choosing a point set Pn=u0, ⋯, un-1∈[0,1)t , and then the average value of f over Pn is computed, i.e., we get the estimator Qn=1n∑i=0n-1f(ui) In Monte Carlo method, the points u0,…, un-1 are independent random vectors and uniformly distributed over [0,1)t and n is the number of replications (a constant). This estimator is unbiased and has variance σ2/n , and define σ2=VarfUi, where VarfUi=∫[0,1)t f2udu-μ2 (3.2) If σ2<∞ , then Qn obeys a central-limit theorem, and we can rely on it to compute a confidence interval on μ , whose width converges roughly as Oσn-1/2.

The use of MC for pricing financial options was first proposed by Boyle. Since then the approach have evolved quite greatly. In practice, one uses a pseudorandom number generator to choose these points. The idea of quasi-Monte Carlo methods is to use a more regularly distributed point set, so that a better sampling of the function can be achieved.

An important difference with Monte Carlo is that the set Pn is typically deterministic when a quasi-Monte Carlo method is applied. In other words, Quasi-Monte Carlo replaces the independent random points Ui in (3.2) by a set of n deterministic points, Pn=U0,⋯, Un-1, which cover the unit hypercube [0,1]t more evenly (uniformly) than a typical set of random points. The point set Pn is called a design by some statisticians. Niederreiter presents these methods in detail in his book, and describes different ways of measuring the quality of the point sets Pn on which quasi-Monte Carlo methods rely. More specifically, the goal is to measure how far is the empirical distribution induced by Pn from the uniform distribution over [0,1]t .

Such measures can be useful for providing upper bounds on the deterministic integration error ∣Qn–μ∣ . Typically, a point set Pn is called a low-discrepancy point set if D*(Pn)=O(n-1 logtn) . For a function of bounded variation in the sense of Hardy and Krause, the integration error ∣Qn –μ∣is in O(n-1logtn) when Pn is a low-discrepancy point set The upper bound states that the advantage that QMC methods have over MC is that QMC has a probable error in O(n-1/2) which will ultimately be lost as the dimension t increases. Consequently, it suggests that quasi-Monte Carlo methods will require a sample size n too large, for practical purposes, to improve upon Monte Carlo when t is large.

In this context, the programming codes for QMC simulation on several assets are too much complicated, then numerical results showing an improvement of QMC over MC in high dimensions and using a relatively small sample size n seem hard to explain.

Chapter 5: Comparisons of Pricing Models

Throughout this thesis, we have reviewed the various pricing methods that can be used on American options. The pricing of European options is rather deemed as being easy and accurate due to the fact that they expire only at maturity and are hence done through the Black-Scholes equation. This is not the case for the American option due to its ability to be exercised any time before and on the expiration date. As such, numerous mathematicians and analyst have come forward to present multiple models to price the latter, the most famous being the Black-Scholes, Boundary formulation and the Monte Carlo simulation.

First to be analysed was the binomial model. The binomial model is rather very easy and simple to use. With its various conditions like the price would move in only two directions; up and down, it can be assumed that it is very easy. However, the problem arises when we have to price multiple assets over periods more than 1, then it becomes much complicated and time-consuming to do so.

The same would go for the trinomial model, where instead of two, the price would move in either three directions; up, down or no change. This model however is more adapted to real life situations. The binomial model calculates the option prices at each next step. As such if there are any adjustments to be done such as an early exercise of the American option, it can still be adjusted and worked through at that specific time. The binomial is among one of those who calculates by working backwards, till we are left with only one option price.

It should be noted that in the case there is no alteration to the model and that the same inputs are used as in a Black-Scholes model, with the help of sufficient steps, both the Black-Scholes and the binomial model would look alike. The main difference between these two is that the binomial model offers a greater flexibility than the Black-Scholes as the inputs can be changed at each step in order to process for differences arising while exercising a particular option.

Longstaff and Schwartz introduced their well-known pricing algorithm for American options in [Fa01] based on a dynamic programming formulation. The Longstaff- Schwartz algorithm uses a backward iteration where at every timestep the continuation value of the option is approximated with least squares fit against a set of basic functions. Most tree based methods to approximate the value of an American option are also based on backward iterations. Such methods are simple yet powerful pricing tools.

With a Monte Carlo approach pricing and managing the risks of American derivatives is far more involved than pricing and managing the risks of European options. The added difficulty stems from the fact that it is a priori unclear when the option holder will choose to exercise the option. Among all the pricing methods that work backwards, the Monte Carlo is the only one to be working forward in order to price options. As such, it uses computerised modelling to predict outcomes. At first the model generates a random number based on a probability distribution. The number then uses additional inputs of volatility and time to expiration to generate a stock price. The latter is then used to calculate the value of the option. In turn the model will keep generating results each time using a different set of random values from the probability functions.

Depending on what model of Monte Carlo we are using, the number of uncertainties and probability distribution used, the simulation can generate a thousand of recalculations before it is completed. Monte Carlo simulation generally would take the average of the all the results as the option price.

Conclusion

The purpose of this thesis was to attempt to price American options using various pricing approaches and to compare them to the Monte Carlo Simulation. Also, we concluded that among the many Monte Carlo approaches, using the Least Squares Monte Carlo method is more suitable in solving problems of bigger size.

While the pricing of European options have been quite easy due to the fact that it can only be exercised at maturity time, it has been rather difficult to do the same with American options. In fact, over the years many mathematicians have devised many strategies for pricing the American option. Due to the fact that underlying dynamics can be very complicated, the analytical models for option pricing involve a lot of restrictive assumptions.

Coming to real-world applications, we use numerical methods that can approximate options, notably for American options. These include the valuation of options, the estimation of their sensitivities, risk analysis, and stress testing of portfolios. However, in recent years numerical experiments have become a lot complicated in financial theory and practice has increased enormously. putting more demands on computational speed and efficiency, giving way to further develop and enhance the methods.

We have seen as well how the risk-neutral valuation model can be a valuable tool in the future to accurately price options due to the rapid advancement in computational technology. The pricing of American options remains a very interesting research area, especially while using Monte Carlo techniques. The Monte Carlo method is best used in handling complex and big options. In the near future, we would be able to value American options with much ease as the simulation techniques of the Monte Carlo method are becoming broader and promising, particularly while dealing with multiple factors in the market. When options are traded, they are often done so in bulk rather than single. As such, to price each and every one of them can be quite tiring and time-consuming.

As far as calculations are concerned, I personally feel the use of Binomial model would be a perfect tool for pricing as it is simple and easy to use. The only problem though would come with multi assets over multiple periods of time. As such one can hope to use the Monte Carlo to calculate heavy portfolios and assets Its ability to calculate hefty input at high speed makes it one of the most sort out model for option pricing. So much that there have been a lot of derivatives from the original simulation.

In case of heavy inputs, I would say that the Monte Carlo model is the perfect model to price options However.in order to correctly execute a Monte Carlo simulation, one must have more than basic knowledge about unlike the binomial model which require very basic knowledge. Although, the Monte Carlo is becoming more a computerised system and is advancing increasingly in terms of technology. The world has become a very unstable financial and economical place.

Over years, there have been some deep impacting events that have had damaging effects on the global financial health. Events such as the great recession, multiple terrorists’ attacks over the world, and the recent Brexit situation have cause major fluctuations. As such the market would be fluctuating a lot. One can only rely on the effectiveness of risk analysts and market watchers as to not further get in to financial debts.

These analysts and watcher in turn depend on the reliability of such models to correctly price options and a make a reasonable gain from it and limit the loss to the minimum. As such, in my opinion, due to the fact that there are a lot of software being developed and these models being implemented on them, in the coming decade the pricing of American option is particular would be made quite accurate and quick. One such model would be the risk neutral valuation and the Monte Carlo simulation.

References

[And09] A. Pascucci February 2009: “A short course on American options”, web:http://www.dm.unibo.it/~pascucci/web/Ricerca/PDF/american.pdf

[Boy77] P. P Boyle. Options: A Monte Carlo approach. Journal of Financial Economics, 4:323–338, 1977.

[Boy97] P. P Boyle, M Broadie, and P Glasserman: Monte Carlo Methods for Security Pricing, pages 1267–1321. 1997

[Carr98] P. Carr, “Randomization and the American Put,” 1998, Review of Financial Studies, 11, 3, 597–626.

[Cle02] E, Clement. D, Lamberton. P, Potter: 2002, “An analysis of a least squares regression method for American option pricing”.

[Dam09] D. lamberton September 2009: “Optimal stopping and American options”.

[Dew93] Dewynne, J. N., Howison, S. D., Rupf, I. and Wilmott, P.: 1993, “Some mathematical results in the pricing of American options”, European J. Appl. Math. 4(4), 381–398.

[Dup98] B Dupire, editor. “Monte Carlo: Methodologies and Applications for Pricing and Risk Management”. Risk Publications, London, 1998.

[Fra01] Francis A. Longstaff and Eduardo S. Schwartz. Valuing American options by simulation: A simple least-squares approach. Review of Financial Studies, 14(1):113–147, 2001.

[Gla04] Paul Glasserman: “Monte Carlo Methods in Financial Engineering”. Springer, 2004.

[Hir03] A. Hirsa: “Why Be Backward: Forward Equations for American Options”, January 2003, 103–107

[Hull03] J Hull: “Options, Futures and Other Derivatives”. Prentice Hall International, fifth edition, 2003.

[Jar92] R.Jarrow, R. Myneni: “Alternative Characterizations of American Put Options,” (with R. Jarrow and R. Myneni), Mathematical Finance, April 1992, 87–105.

[Joo07] Joonhee Huh.: “Computation of Multivariate Barrier Crossing Probability, and Its Applications in Finance”. PhD thesis, University of Waterloo, 2007.

[Kar88] Karatzas, I.: 1988, “On the pricing American options”, Appl. Math. Optim. 17, 37–60.

[Kie52] J. Kiefer and J. Wolfowitz.: “Stochastic estimation of the maximum of a regression function”, Annals of Mathematical Statistics, 23(3), 1952.

[Kim90] Kim, I. J.: 1990, “The Analytic Valuation of American Options”, The Review of Financial Studies 3(4), 547–572.

[Kir83] S. Kirkpatrick, C. D. Gelatt, and M. P. Vecchi.: “Optimization by Simulated Annealing. Science”, 220(4598):671–680, 1983.

[Kus98] Kuske, R. A. and Keller, J. B.: 1998, “Optimal exercise boundary for an American put option”, Applied Mathematical Finance 5, 107–116

[Mus98] M, Musiela. and M, Rutkowski.:1998, “Martingale Methods in Financial Modelling”, 19, 48-50

[Qui09] Q.Jia June 2009: “Pricing American Options using the Monte Carlo Methods” web: http://www.diva-portal.org/smash/get/diva2:301061/FULLTEXT01.pdf

[Rac98] Rachel A. Kuske and Joseph B. Keller: “Optimal exercise boundary for an American put option”. Applied Mathematical Finance, 5(2):107–116, 1998.

[Rob51] H. Robbins and S. Monro: “A Stochastic Approximation Method. The Annals of Mathematical Statistics”, 22(3), 1951.

[Rog02] L. C. G. Rogers: “Monte Carlo valuation of American options”. Mathematical Finance, 12:271–286, July 2002.

[Rog97] L.C.G. Rogers and D. Talay: “American Options: A Comparison of Numerical Methods”, in Numerical Methods in Finance, ed. Cambridge University Press, 1997, 67–87.

[Sin10] Euan Sinclair: “Option Trading, Pricing and Volatility Strategies and Techniques”, Wiley, 2010.

[Tho00] Thomas Little, Vijay Pant, and Chunli Hou: “A new integral representation of the early exercise boundary for American put options”, Journal of Computational Finance, pages 73–96, 2000.

[Wil93] P Wilmott, J Dewynne, and S Howison: “Option Pricing: Mathematical Models and Computation”, Oxford Financial Press, 1993.

[Wu97] Wu, L. and Kwok, Y. K.: 1997: “A front-fixing finite difference method for the valuation of American options”, Journal of Financial Engineering 6, 83–97. Web: http://fedc.wiwi.hu-berlin.de/xplore/tutorials/sfehtmlnode40.html