1. Background

Developing disaster management strategies, evacuation plans, and safety guidelines has been an active research area for long. Technology and methodologies for emergency evacuation planning have grown with last forty years’ of research. In August 2005, one of the most hazardous hurricanes in the history of the United States, Katrina, struck the Gulf Coast. As per a report published in 2006 by the United States Congress, it resulted in over 1700 deaths and estimated loss of property worth $81 billion. Many post-hazard investigations have concluded that ineffective evacuation attempt was a major contributor to the high number of deaths in New Orleans, which means that effective evacuation could have saved lives. The reasons are not clear that why but surely a planned and tested evacuation plan can make evacuations more effective.

A little after Katrina, in September 2005, Hurricane Rita approaches the Texas Coast and since people were aware of the disastrous effects of Hurricane Katrina, they were threatened. It resulted in the largest evacuation in the U.S. history with thousands of people evacuating, stuck in a large traffic jam. In Houston however, based on the recent disaster experience, the local and state emergency management institutes had already set up effective evacuation routes. Regardless, the transportation system was crowded by many vehicles resulting the evacuation routes and its vicinity in giant traffic deadlocks, and evacuees were stuck in it for about long time.

Post-hazard surveys have confirmed that the current state of planning and execution was not well-prepared for such an unprecedented and mass emergency in Houston, Texas. Per Soika K. (2006), Mayor White quoted that such a massive contraflow “was not in state plans and took almost 12 hours to implement by the relevant agencies.” This inspires and necessities disaster managers and planners to reexamine the existing evacuation procedures and develop a more comprehensive model for large evacuation.

Evacuation planning consists of some interrelated components like delimiting of the evacuation area, identifying safe zones and shelter locations, evacuation routes configuration and more. An insightful plan should be developed before a disastrous event. This means, evacuation planning must include status (working condition vs/ work in progress) of all available road infrastructure and related resources. The plan should be frequently reviewed and updated to include new routes and exclude broken roads to optimally utilize available transportation network. Not limited to this, if a model can determine evacuation/shelter decision would be more useful, since they prevent unnecessary evacuation from happening.

This work presents different methods evacuation modeling and represents the need of comprehensive evacuation planning in a more literary way. The next section presents briefing about evacuation planning and its components.

1.1 Evacuation planning and factors

Evacuation is intentional escaping of people from an area under threat of a natural or man-made disaster. Evacuation can be on a small or large scale depending on the hazard type and area under threat. For example, escaping from a building on fire, a city under hurricane threat or a nuclear accident are all evacuation of different scales. Thus, the scale and nature of evacuation depends on type and intensity of hazard and evacuation ground/area. The people escaping an area are called evacuees. This paper presents traffic network evacuation models approaches as in evacuation from a rural or urban area. Emergencies tend to occur during hazards and evacuation is sometimes the only effective rescue measure. However, with growing population and continually expanding city limits, proper planning has become essential, which can also be integrated with the hazard prediction methods. Evacuation reduces life-loss in both predictable or unpredictable hazards. With technology, the accuracy of forecasting has increased which is advantageous for evacuation planning point-of-view. In the case of unpredictable events like terrorist attacks, evacuation still is a post-impact preventive measure.

The objective of an evacuation plan is utilizing existing transportation system and its resources to maximize successful evacuations. Evacuation planning can also be incorporated in designing a transportation system from scratch. As Leonard R. (1985) says, evacuation in a city or town can occur due to natural hazards like floods, earthquakes, tsunamis, epidemics etc. or manmade hazards like terrorist attacks, fires etc.

1.1.2 Factors of evacuation planning

I believe that three of the most important and necessary events/factors in evacuation are sheltering, communication, and transportation, which are discussed in this section.

The primary consideration before preparing evacuation plan is identifying evacuees, estimating their number, characteristics and behavior during evacuation. Several studies indicate that evacuating population is a broad group of individuals with different income levels, age groups, physical/mental abilities and disabilities, and language proficiencies. For convenience of this paper, evacuees are defined as individuals who depend on road-network transit to escape and avoid disaster situation.

Further in this section, we present three important factors in evacuation planning: sheltering, communication and transportation. In no particular order and not limited to, their significance in evacuation planning is follows:

1.3.1 Sheltering

During major disaster events, a shelter can be anything from hotels/motels, a friend’s home, school, hospital, specially built public shelter houses, or your own home if you have a special sheltering facility at home.

An important task before building sheltering facilities is estimating the number of individuals that might use them, which again takes into consideration many factors and can change situationally. Furthermore, shelters are prepared based on the length of possible evacuations and if evacuees are residing in surrounding counties. Examples of common shelters are malls, schools, indoor parking lots, hotels and any solid building with large open indoor spaces that are not susceptible to storm/ rain surge or flooding. Note that not all shelters have to be designed specifically as shelters but existing buildings such as above can be safely used as designated shelters for that situation.

Information about shelter locations should be publicly available and well known to surrounding residents. Such information can be broadcasted on local radio, television, text messages and pre-recorded phone calls periodically. However, shelters should be protecting from pre or post-hazard events such as flooding, wind-damages or simply suffocation due to over-crowding with evacuees. Thus, total capacity of every shelter should be predetermined and made visible on shelter entrances. In addition, shelters should have enough basic resources such as food, water and hygiene to accommodate predetermined number of evacuees. This means having enough storage space for food as in refrigerators or cabinets, cooking space and sometimes vending machines for ready-made snacks and drinks. For this reason, schools are often used as disaster shelters since they are made of solid material, have break rooms and cafeteria and are big enough to accommodate more evacuees.

However, it is important to consider other factors before using a building as a disaster shelter. Following are few such factors to keep in mind before using a building as a shelter or building one from scratch:

• Should be protective from pre or post hazard generated harmful events such as flooding, fire or fast winds.
• Should not have or be cleared of the following:
  • Fall hazards: such as ceiling fans or other suspended objects
  • Flying objects: such as glass bottles and cups, wooden sculptures or pallets, tools or knives, loose electronic devices. Disposable utensils of paper or foam can be used.
  • Fragile material: such as window glass, that can break and come apart, become a flying object and can be injuring to life threatening.

• Should have enough hygiene facility for maximum number of evacuees that can be accommodated.

• Should have enough medical supplies and first aid facilities and preferable be close to a hospital and transportation facility should be available.
• Should be equipped with emergency tools such as fire extinguishers.
• Should have mounted phones available to call in case of emergency, and necessary personnel that are trained CPRs and first aid.

It is important that local sheriff and hospital are aware of shelters’ locations and informed of the number of evacuees sheltering. Moreover, for the shelters where hospitals are farther or are sheltering large number of evacuees, ambulance can be parked standby for any emergencies. Some shelters may need to provide medical supervision or care to evacuees. Such specialized shelters have to be specially designed. Sheltering planning (and evacuation planning) are not limited to just providing necessary facilities and resources but much comprehensive than that.

1.3.2 Communication

Evacuation planning is a comprehensive event that is comprised of many factors. Thus, it is difficult to plan for such events just by one or two organizations. It is important to keep participating non-profit organizations and church groups in loop while planning. This is where effective communication is required while setting evacuation/sheltering plan, and during the actual evacuation event. Effective communication prior, during and after the disaster make evacuation resilient and avoid failures.

Information that can be exchanged among participating organization during planning phase are number of possible evacuees, number of shelters and their locations, road capacities, most updated road network, possible shelters in case of more evacuees than expected, emergency medical and other supplies, most effective transportation phase during medical emergencies while evacuating/sheltering, closest hospitals, designated drivers etc. Information that can be broadcasted to evacuees are nearby shelter locations, shelter capacities, things to carry while evacuating, quickest routes, blocked routes, traffic situation, status of the disaster itself and related emergency information. Evacuees can also be made aware of local organizations or authorities to contact in case of any concerns.

Communication with large population can be challenging, especially in a diversified nation like the United States, where people from all over the world and languages reside. In many cities and towns, it may seem necessary to broadcast evacuation messages in languages other than English and Spanish for evacuees who speak a different language or are special needs. For example, participating organizations can make videos of evacuation/sheltering message in American sign language (ASL) and broadcast over televisions and social media.

Some of the current practices in broadcasting hazard evacuation and sheltering messages shall be discussed in late part of this book.

1.3.3 Transportation of evacuees

In event of evacuation, a major population is self-evacuating individuals and transportation networks and needs should be considered for such individuals. Some of the factors that must be considered in a transportation plan is hurricane path or disaster location, number of roads active or under work, capacities of roads in traffic network, average wait times at road intersections and travel speeds.

Moreover, in relatively big traffic networks, we also need to consider all combinations of evacuation paths from different evacuation regions in the network to preferred or predetermined safe zones or shelters and recommend the best one. For this, we are required to determine a variable that determines the choice of evacuation path, for example, minimum travel time or maximum average speed. Also, many advanced level evacuation simulations recommend safe zones and evacuees can choose a preferred safe zone rather than directing all evacuees to one predetermined safe zone. This opens doors for evacuees to spread out in different safe zones rather than jamming evacuation routes leading to just one or two predetermined safe zones. While planning evacuation, it is important to concern recommended state/federal or city guidelines about evacuation, which may vary from every state or city and for disasters of different strength

Another class of evacuees that also needs to be addressed are transit dependent individuals are evacuees, who are dependent on local transit and do not own personal vehicles at all or not in capacity to evacuate. Assuming that they cannot obtain personal vehicles, rentals, buses or other public transport are required to take them to a safe zone or shelter. Cities are required to provide buses and drivers in enough capacity or rental vehicles, which are often acquired by mutual agreements between companies, adjacent states or cities.

2. The Problem Statement

This study focuses on presenting and testing of transportation network optimization models, calculating evacuation variables in different capacities.

There are different types of emergencies where evacuation is necessary for threat-mitigation. Thus, evacuation models can be classified based on parameters like geographical applicability, time span and nature of emergency. For example, a fire hazard may require evacuation in a small residential region but a nuclear hazard may require people in ten-mile radius to evacuate. The first case does not require intensive evacuation planning but the second case, because of the larger emergency-zone, requires more intensive planning. Thus, larger area requires well-planed and tested evacuation model. In the same context, an area with high population density or less transportation capacity also requires well-structured and tested evacuation planning. In our case, a city sized disaster as hurricane may affect a very large region and hence necessitates well optimized evacuation planning model considering a variant like traffic network optimization. In terms of time span, evacuation model may be applicable to short/ long term and frequently/infrequently occurring incidents.

In this study however, we are presenting three well-known traffic network modeling approaches of different times and capacities. The applicability of these models would be in solving Short Notice Evacuation Planning (SNEP) problems as presented in Lim, G. J. et al. (2012). For this, we present the three approaches and program/solve for some important parameters based of the presented models. By solving these parameters, we can extract important data points usable in solving network optimization problem of any form Ford, L. R., & Fulkerson, D. R. (1958)

This paper consists of ……………………

3. Literature review

There are various traffic assignment models that provide solution for transportation network using different mechanisms. Most of the literature on traffic assignment models deal with the steady state problem of finding link flows from an origin-destination trip matrix. Time-dependent traffic assignment on a transportation network has not been widely studied in the transportation 1iterature Sheffi, Y., Mahmassani, H., & Powell, W. B. (1982). A traffic assignment problem solves parameters like traffic density and flow, average speed and queues on network links based on inputs like origin-destination matrix and relevant characteristics of the transportation network. These parameters are presented as a function of time.

A disaster management strategy has few steps and each step can have a series of activities. Without systematic planning and implementation of these activities, disaster management can be counterproductive. Every step of disaster management strategy can be simulated or planned in a model, which are tested and interconnected for flawless execution.

3.1  Components of Evacuation Planning

The four steps of evacuation planning are initial warning, individual preparation, network clearance and evacuation verification. Initial warning is broadcasting the evacuation order to the affected population through various means. This is the information that is the first broadcast. Individual preparation is the activity where individuals after being warned, prepare to evacuate. Network clearance is the time it takes for the evacuees to reach to the safe region. The final component is evacuation verification where the result of the process is reported and the evacuation order is lifted.

The four components add to the total evacuation time. The total evacuation time is a function of:

Total evacuation time=F {initial warning time,

indivicual preparation time, network clearence time, evacuation verification time}.

These account for the time taken to send, receive and act on an evacuation order, preparation time in evacuating people, time to reach to safe destinations, and verifying and lifting evacuation order. ‘Initial warning time’ is dependent on the emergency warning arrangements, sensing system and broadcasting system and so is independent of network modeling. Similarly, individual preparation time depends on situation and willingness of individuals and so is independent of time-estimation model. Evacuation verification time, the time required to verify if the evacuation is conducted safely and effectively is an important post-evacuation test.

The test ensures if the situation is under-control and if the evacuation order can be lifted. The final activity in the process is to send an evacuation lifting order. The test can be simulated and predesigned for every evacuation situation and it has five test statistics: geometry, scenario, expected result, test method and user actions. Geometry tests are tests conducted for different evacuation configurations and geometry. Scenario simulates all possible evacuation scenarios in a simulation model, which will be discussed in the upcoming sections. Expected result is the qualitative or quantitative result that the evacuation model would produce at the end of the test and actual evacuation run. Test method discusses in detail that how the expected results would be produced. It has two parts: qualitative: visualization of the evacuation behavior, and quantitative: comparative study of evacuation flows and times. The final part of the test is user action, which is set of actions required on the tester side while performing a test.

Since network clearance time takes most of the evacuation time, it is significant to optimize it. Thus, the models and methods presented will focus on estimating ‘network clearance time’. Also, network clearance models can be updated and replicated in different areas.

The first three are dissipation rate model, manual capacity analysis, and traffic-simulation models. These three models are foundational for NETVACL presented as macro-traffic simulation model.

Note:Since calculation of network clearance time is our primary focus, spatial and temporal profile of the network loading pattern are essential to know to perform simulation. Spatial profile is the actual geometry of the evacuation area, and temporal profile consists of flow patterns, waiting times, dissipation rates etc.

3.2     Dissipation rate model

This model is proposed by Houston in 1975 and is a simplistic model for estimating evacuation time Houston, W. (1975). The model is a simple correlation between size of the evacuation area and population density, with total evacuation time. Hans, J., & Sell (1974) compiled the data used by Houston, T.

A negative exponential function was assumed for traffic delay at network intersections, with a constant flow rate of 10,000 people per route. The model includes two parameters: Ԑ, which is inversely proportional to the population size, and ἢ, which is statistically correlated to evacuation times reported.

This model is simplest to use among all the models presented here. However, complex models and simulations often use simplistic assumptions of dissipation rate. The approach does not account for location variables like network design, population distribution, intersection capacity etc. Also, the data set is for the evacuation areas with poor warning systems.

Thus, the model is meant for smaller evacuation areas and is effective in simple networks because of negligible calculation time. For detailed analysis and planning for complex networks, following modeling and simulation methods are effective.

2.3     Manual capacity analysis

This is a set of traffic modeling methods used by different analysts at different times and places. Two examples of manual capacity analysis approaches are study of evacuation by Wilbur Smith and Associates. (1974)  and Stone and Webster Engineering Corporation. (1980). Under these studies, road capacities of all roads in areas of study were calculated based on traffic engineering procedures according to Highway Research Manual. (1980). . The next step was identifying all possible evacuation routes in each sector and assigning population to these routes. Clearance times can be calculated from this data as

Clearance times=Total number of vehicles assumed to participate in an evacuation routeTotal capacity of the route.

Above equation predicts average clearance times for each route. The method used in both studies was similar and requires analysts’ arbitrary judgment.

Manual capacity analysis procedures are static and inaccurate for big networks. They fail to capture important network effects and interrelationships like intersection delays, route choice decisions and grid locks. Also, the traffic congestion and considerable fall of average vehicle speeds reduces link capacities. Since the roads are not made to operate under evacuation, congestion also reduces throughput of the evacuation routes.

Though, manual capacity analysis techniques are inaccurate for large networks, they are effective for small town networks and other evacuation approaches such as building evacuation. The simplicity of the process and fast calculation makes their application easier.

2.4     Traffic simulation models

Sheffi, Y., Mahmassani, H., & Powell, W. B. (1982) state that when the iterations are made in a computer software periodically or on a continual basis, it is called simulation modeling.Transportation system simulation is a mathematical model in computer software and contains all network parameters like freeway intersections, roundabouts, arterial roads, downtown grid etc.. Traffic simulation models help planning and operating a transportation network and is an important discipline of transportation planning and traffic engineering study started about forty years ago. Thus, many transportation agencies and disaster management institutions also use traffic simulation models in managing traffic network.

To understand any simulation model, it is important to know its system state, a set of variables that describes the simulation system over time. System states are categorized as discrete and continuous. Similarly, simulation models can be classified as discrete and continuous over state and geography.

An important application of traffic simulation models is in evacuation planning. Monte Carlo model is one of the earliest discrete event simulation models, followed by cellular automata model that uses deterministic rules. These two models were widely used and were improvised through further research and experiments Rubinstein, R. Y., & Kroese, D. P. (2016).

More recent techniques use either continuous-time simulation or discrete events simulation. Discrete event simulation models are dynamic and stochastic. These models include time as a variable (and thus, overcome the shortcoming of manual capacity analysis models). The models required to have a state, input and output trajectories for each calculation time interval. Know that discrete event simulation models work in terms of time intervals and an iteration takes place for that time-period.

Continuous time simulation methods can solve similar problems, except that the time variable is continuous and the system keeps iterating the data in a continuous sense. Continuous time simulation models use differential equations and numerical integration methods. The equations can use simple iterating methods such as Euler’s method to high order Runge-Kutta or Heun’s method. Feel free to refer to Greenbaum, A., & Chartier, T. P. (2012) for detailed application of the above mentioned methods.

2.4.1     Micro traffic-simulation models

Micro simulation modeling is a continuous type simulation and tracks movements of individual vehicles. One of the ways micro simulation works is by generating and assigning random numbers to vehicles and determine their behavior. Therefore, it necessitates running several iterations with ‘random number seeds’ to determine routing decisions with desired accuracy. The period when the system is running initial iterations before it reaches a steady-state is called warm-up period and its results should be excluded from a system report.

Micro simulation models generate two types of results, numerical outputs and animated displays. Numerical outputs need to be interpreted by understanding how the data is accumulated and results are calculated and summarized. Animated display output allows analysts to assess the system performance quickly. One of the limitations of animated displays is, some system insights like minor but important changes cannot be displayed. This limits the results to being qualitative.

A disadvantage of animated displays is formation of a ‘result queue’ or a series of results to be displayed for a continuously iterating system. This means the display must be processed fast and constantly updated.

An important performance evaluation mark of mirco-simulation technics is Measures of Effectiveness. Measures of Effectiveness (MOEs) are performance statistics and a set of variables that demonstrate how well the system is characterized to the desired performance. MOEs are unique to each simulation model.

Sokolowski, J. A., & Banks, C. M. (2009) define the following MOEs as most commonly used when analyzing the extent to which every system alternative meets the project goals:

• Link section capacities, speeds, traffic density, travel time, queue length
• Intersection turning ratios and delays
• Loop detector records for occupancy, gap, speed and headway
• Vehicle travel paths, speed vs. distance plots.
• VMT and VHT (Vehicle Miles Traveled, Vehicle Hours of Travel)
• Mean System Speed = VMT/VHT
• Total system delay

VMT is a result of total number of vehicles in the system, and the distance they travel. VHT is a product of link travel time and link volume over all the network links.

In order to calculate total system delay, it would be required to define a baseline that what level of traffic congestion leads to major delays, or the minimum delay that is considerable. Some consider it as any delay that is above free flow conditions. A major disadvantage of micro traffic-simulation models is higher calculation time. Tracking each vehicle with a continuously iterating system generates streams of data. However, macro simulation models are dynamic and break the limitations of conventional dissipation rate or manual capacity analysis models.

To improve on inaccuracy of static traffic simulation models, several attempts have been made by integrating results using different methods. The purpose of developing micro-traffic simulation was to analyze traffic control strategies in smaller areas. Micro-simulation requires much details in representing intersections, roadway links and controls. Every vehicle in the system is tracked by the model. The tracking is not just limited to movement of a vehicle in the traffic network, but related characteristics like vehicle type, average speed, travel times and driver’s decision behavior under various traffic conditions is also recorded. Such detailing would take tremendous processing power and consume considerable amount of time in generating meaningful results, when applied to big cities of today.

One of the advantages, however, of using micro-simulation is, the computerized process is very consistent in repeated applications and shows about same level of sensitivity and accuracy to different analysis situations. Such methods have been validated by different traffic network studies and analysts and is known to show a reasonable accuracy and agreement with observed traffic behavior, per Sheffi, Y., Mahmassani, H., & Powell, W. B. (1982). Also, Texas Highway Operations Manual (1992) has used micro-traffic simulation NETSIM. The validations of such techniques are limited to rural and small urban traffic networks under normal traffic conditions. However, traffic may not be under exact normal operation in face of evacuation order.

Thus, a realized disadvantage of such models is its limited capacity and applicability due to its micro-simulation nature. The technique requires high speed computers and other computational resources, and sometimes, required computation capacity exceeds available resources for real life evacuation problems. This adds computational costs and waiting time for slow computation in case of complex or big networks.  With this, it also requires analyst team to input turning movement and turning ratio at each intersection, based on historical observation. This means that it does not allow a dynamic route selection or in simple words, cannot update turning movements based on current traffic behavior.

However limited micro traffic simulation may look in perspective of big city comprehensive traffic problems, it has surely added a lot of research value and applicability toward macro-traffic simulation, and one such important model NETVACL.

3. Dynamic iterative traffic simulation modelling

This section describes macro-traffic simulation and dynamic modeling, two important techniques for accurate and fast calculation for evacuation planning. Macro-traffic simulation uses a set of equations to define a traffic network and evacuation constraints. Dynamic nature of model considers queue formation at intersections, traffic patterns and variety of alternative evacuation scenarios and is more appropriate for planning real life evacuations.

Modern macro-traffic simulation models also consider weather options and routes, intersection controls, and other lane management strategies. Because of its parametric nature, the model takes less computational time and costs.

3.1     NETVACL Model

NETVACL is a dynamic route selection macro-simulation model that uses traffic flow relationships and evacuation constraints to simulate vehicles flow in a network. The mathematical relationships are based on vehicle speeds, traffic densities and flows, spill-backs, queue lengths and other traffic variables. The model uses a set of arcs/ links and nodes to represent the network. Arcs (also called links) are individual roadways and nodes are intersection, each designated by a variable. Unlike NETSIM and other micro-traffic simulation model, NETVACL does not keep track of individual vehicle movements and related characteristics. Since traffic flow is heavy during evacuation, the deterministic nature of NETVACL makes it fast, relatively accurate and applicable to evacuation in big or complex networks.

Using mathematical description of transportation network, safe and unsafe areas, and rates of originating traffic, NETVACL gives an insightful account of traffic behavior on an evacuation network throughout the simulation. This section introduces the general structure of the model and its basic features; priority flow-treatment at non-signalized intersections, dynamic route selection feature, and capacity calculations.

3.1.1     Structure of NETVACL

NETVACL model has four units or procedures; main program, data procedure, preprocessor and model simulator. Main program looks over execution of the simulation by managing the calls between procedures and the simulation itself, and reports the network condition periodically.

Main program also controls the simulation time by turning simulation on/off for different area sections when required or until elapsed time of the disaster.

Data procedure unit processes the network inputs and parameters to be used in simulation by using list processing, a technique to store network variables. For example, the list of all network links is stored with forward/backward pointers, establishing relational database between links and nodes associated with it. This makes the network structure database easier to extract. Thus, the list processing technique of data storage is a key to NETVACL’s high computational ability, reducing computational costs by seventy percent or more compared to NETSIM.

The third unit in the model execution, preprocessor procedure, transforms the physical link and node description into link capacity, speed and density measurements. For each network link, the unit calculates two types of capacities:

Section capacity: Maximum vehicle holding capacity of the link, regardless of upstream or downstream network restrictions.

Approach capacity: vehicle holding capacity of the link considering downstream network restrictions and queue at the downstream node.

Clearly, on a real-time traffic network,

Approach capacity=Section capacity-Queue length.

Once the preprocessor converts physical description of network components into mathematical data, data preprocessor runs an iteration to ‘list process’ the data again and update the lists and relations.

Note: Section and approach capacities are defined differently in different studies. In standard traffic engineering, section capacities are highway capacities and approach capacities are associated with streets signalized intersections. Above definition is applicable to all the models presented in this work.

The capacities play an important role in calculating network clearance times. In simple words, section capacity is the upper bound of number of vehicles on a link, and the link approach capacity is the actual vehicle flow, restricting actual number of vehicles that can move along that link. However, vehicles that can move along the link but cannot cross the intersection are assigned to ‘queue’ associated with that link.

The simulator unit runs iterations over data converted by preprocessor and list processed by data processor unit, by using two logical sequences: node pass and link pass. The passes are made through the data set on a relational basis using mathematical equations. The link pass is for traffic flow through the links while the node pass is for traffic flow between the links.

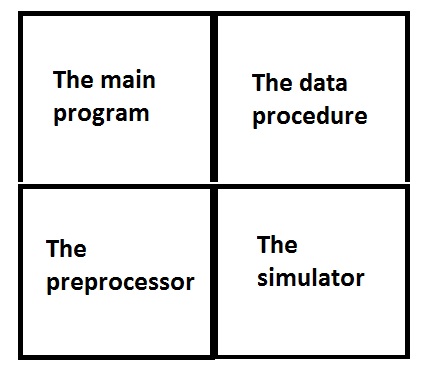
Figure 2 The four units (procedures) of NETVACL

3.1.2     Dynamic Route Selection Approach

Unlike NETSIM, NETVACL does not utilize a predefined turning movements’ set at each not, but determines nodal turning movements as a function of link-directionality and varying traffic conditions. It is assumed in the model’s dynamic route selection approach that drivers chose a direction based on how fast that direction or route can take them to a safe area. Also, drivers consider two scenarios in route choice decision: prior knowledge of the traffic network under consideration and link characteristics, and a view about then traffic conditions.

The model considers drivers’ first route choice scenario in its preference factor, which is a user-defined factor specified for all network links, and the second scenario is captures by average vehicles speeds on outbound links.

The assumption laid under this is, a driver chooses an outbound link with relatively higher average speed regardless of his/her knowledge of the link network.

3.1.2.1     Route choice mechanism

Further, let PF denote the preference factor, which is defined by user specified preference ratings for each network link. Let j be an outbound link at any network intersection. Let’s say there are a total of k outbound links from that network intersection, and each outbound link has its preference factor. Thus, the preference of choosing an outbound link j over all k outbound links from that intersection is,

PFj∑kPFk .

(1)

Above equation considers only the first scenario of drivers’ route choice decision. When the second scenario is considered, in which is vehicles’ average speed on the concerned link, the equation gives us a probability of that link choice.

Pjt=PFj.Uj(t)∑kPFk.Uk(t)

(2)

Equation (2) is the probability of a driver choosing an outbound link number j out of all outbound links at any intersection or node in the traffic network, during time or iteration t.

Uj(t)is average vehicle speed on link j during time t. Equation (2) reflects hypothesis that probability of choosing a link at an intersection increases as average travel speed on that link increases. This provability is calculated during every iteration for every link in the network. These probabilities help in calculating total flow through every evacuation route.

3.1.3     Link capacity analysis

Capacities in a transportation network reflect maximum number of vehicles that can flow through a link, a route or the entire network itself. To determine total capacity of a route or entire network, individual link capacities need to be calculated. As mentioned earlier, NETVACL calculates two capacities, namely section and approach. Section capacities are constant and predefined. They are upper bound for the maximum flow through a link. Approach capacities are calculated periodically after each iteration, or continuously (when time between each iteration is zero) based on intersection queuing and constantly updated.

Section capacity calculations can be based on approved calculating method of Highway Capacity Manual (HCM) or any other approved method. NETVACL calculated approach capacity for a time-period t by using

Cit=Ci.ALt.ARt,

(3)

where

Ci= section capacity of link i, and

ALt,

ARtare left and right turning ratios, or turning movements of the link flow respectively.

These two factors are functions of percentage of flow turning left/right, approach width, parking or waiting allowance and other HCM defined factors.

Note that, in NETVACL model,

ALtand

ARtare constant values. In real life evacuation networks however, these values cannot be constant.

3.2     The NETVACL Simulator

The simulator executes iterations on the data entered, using mathematical equations and constraints. Each iteration is known as simulation interval and their length is controlled by an operator or analyst. As mentioned earlier, simulator runs in two logical sequences or passes: link and node pass.

Any transportation network is made of links and nodes. The model assigns numbers to each network component and the data procedure unit assigns component characteristics with that component number or ID, creating a relational database. It is important to note that one link represents one lane on a road or street section. This means section of a four-way road would be represented by four links. Nodes represent link intersections, regardless of the number of lanes or links representing them.

A link pass in a simulation interval calculates the number or flow of vehicles that would travel through each link and cross it or join the queue at the respective upstream node. A node pass calculates the number of vehicles that would leave inbound links (links entering a node) and enter outbound links (links exiting a node) for each node in the network for that simulation interval. Thus, at every simulation interval, all the network links and nodes are scanned by link and node pass respectively.

3.2.1 The link pass calculations and Greenshield’s macroscopic stream model

The following section presents the model calculation methodology during link passes. The iteration method is based on Greenshield’s macroscopic stream model, which gives the relationships between vehicle speed, flow and traffic density. Greenshield’s model is very fundamental in traffic engineering.

The link passes determine the traverse volume on each link during a simulation interval. The traffic density

Ktper lane on each link is calculated by the model, by dividing the number of vehicles per lane moving on the link at time t or VM(t), by the link length LD as

Kt= VM tLD.

(4)

Note: The unit of traffic density is number of vehicles per unit length of link.

The average speed in NETVACL model is calculated by the speed-density relationship given by Greenshield’s model. Generally said, macroscopic stream models represent how change in one traffic-flow parameter affects other parameters. Greenshield assumed simply a linear speed-density relationship as in figure 2.

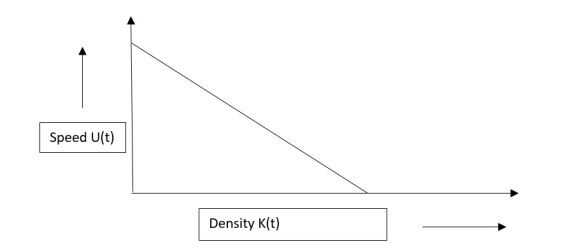
Figure 3 Traffic flow: linear speed-density relationship

Equation (4) defines the density of moving vehicles for a link only in no queue condition, which is usually the case for the first simulation interval. But if a queue of length LQ(t) is present, the flow density for that link is calculated as

Kt= VMtLD-LQt.

(5)

The jam density of a link

KJis defined as the number of vehicles per unit length of queue. It can be calculated by dividing number of vehicles in queue on link i, by queue length LQ(t). After calculating the vehicle and jam density on network links, the model calculates average traverse speed for a link by using the following equation:

Ut=UF.1-K(t)KJ ,

(6)

where,

Ut= average traverse speed on a link at time t, and

UFis mean free speed on the link, which is the average speed at which vehicles travel in absence of traffic. Therefore, according to equation (6), as jam density reduces, average speed increases to mean free speed.

The fundamental relation between traffic flow and average speed defined in Greenshield’s macroscopic model can be used to calculate link flow rate F(t) at time t as:

Ft=Kt.Ut.NL,

(7)

where NL is the number of lanes on the link.

By using the value of flow rate, number of vehicles that reach the downstream node can be calculated, VR(t) at time t or any iteration number as

VRt=Ft.T,

(8)

Where T is the iteration-period or length of one simulation interval in its appropriate unit.

If in any case, VR(t) > VM(t), the model will automatically set VR(t) = VM(t) since number of vehicles that can reach the downstream node cannot be greater than the number of vehicles moving on a link.

The difference between the number of vehicles moving on a link and the number of vehicles that can reach the downstream node gives number of vehicles in queue Q(t) at time t is

Qt=VMt-VRt.

(9)

In the next simulation interval, the updated value of the number of vehicles moving on the link would be

VRt+t1=VRt1+Qt,

(10)

where VR(t₁) is the number of vehicles added to the link in the next simulation interval at time t_1.

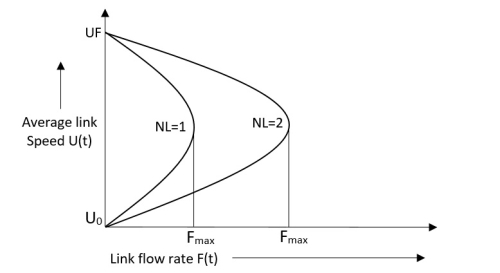The following chart shows the relationship between average link speed and link flow rate at time t. It can be noted that the relationship is parabolic, and foci of the parabola increases as the number of lanes increases.

Figure 4 Average link-speed vs. flow rate

The last step of a link pass iteration is excess vehicular capacity VE(t) at time t, which is defined as the maximum vehicles that can enter the link in the next interval and can be calculated based on the quantities obtained from the above equations as

VEt=LD-LQt.KJ-Kt.NL.

(11)

Excess vehicular capacity is also called approach capacity for the next iteration. The total number of vehicles present on the link in the beginning of the simulation interval at time t + 1 is VE(t) + Q(t).

The output of a link pass is approach capacity of each link, queue length, average travel time and speed on the links. Link pass is the first step of a simulation interval of NETVACL, and node pass is the second step. Once link pass has been made, the model makes a node pass to calculate appropriate node characteristics.

3.2.2     The node pass

The node pass is the second stage of every simulation interval of NETVACL and determines the number of vehicles traveling through each node or intersection of the network, their turning ratios and tracks the number of vehicles entering and exiting the evacuation zone. The results of a node pass is number of vehicles in intersection queues, waiting times, and vehicles added and removed from queue after each simulation interval. Node pass is made for all the network nodes, following a link pass of that iteration. In case of reduced network models, only primary network is considered first.

The first network characteristic calculated in a node pass is traffic volume VW(t) at time t which is the volume of in the inbound link approaching a downstream node.

Traffic volume is the summation of number of vehicles approaching the downstream node in current simulation interval VR(t) and number of vehicles in the queue in previous simulation interval Q(t-1).

Green split fraction is the fraction of time during which an intersection is green/yellow for an inbound link. For example, for a typical four way and one lane intersection with no protected left turns, green split fraction is 0.25 which means, only 25% of times a vehicle on the link can cross the intersection. Note that each lane is considered as a separate link and so, protected left turns are a separate link with its own green split section.

For unsigned intersections, green split fraction can be approximated as

GEit=VWi(t)NLi∑kVWk(t)NLk .

(12)

Above equation is useful in approximating green-split section at unsignaled nodes like four-way stop intersections. The model calculates link approach capacity based on green split fraction as:

CAit=Gi.Cit ,

(13)

where C_i(t) is the approach capacity for a link calculated from equations (2) and (3). The difference between approach capacity and link approach capacity is, the later accounts for green split fraction. The number of vehicles turning left, right or straight is a multiple of the turning ratios calculated in equation (2) and traffic volume VW(t) at simulation interval t.

Some nodes may not have left, right or straight outbound links, or may have more than four links. The outbound links that are not in either left, right or straight direction are considered as diagonal outbound links. Equation (3) can be expressed as follows to accommodate such nodal variations:

Cit=Ci.Plt.Prt.Pst.Pdt,

(14)

where

Plt,Prt,Pst, and

Pdtare percentage or fraction of vehicles turning toward left, right, straight or diagonal outbound links at all the network nodes at time t.

The volume of cars that can be potentially be moved out of link i and moved into some connecting link j through an intersection can be defined as figure 6.

The calculations and methodology discussed in the link pass and node pass of NETVACL simulation model is ran in the model simulator and flow transfer among the network components is calculated. 00

However, the discussion is limited to link and node pass since their calculation is based on Greenshield’s model and is foundational to the capacity calculations used in Capacitated traffic optimization and evacuation scheduling model presented.

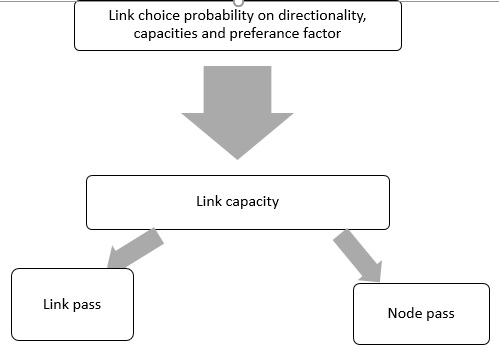
Figure 5 Link Capacity and the passes

Chapter 4 discusses the ‘Capacitated network flow optimization approach for short notice evacuation planning’, which is an algorithmic approach to network flow optimization.