Encryption and AES Network Security Between End Users

CHAPTER 1

INTRODUCTION

1.1 AIM OF THE PROJECT

Our project is mainly aimed at providing the security over the networks between two different end users. Thus, AES algorithm which is a network security algorithm most commonly used in all types of wired and wireless digital communication networks for secure transmission of data between two end users, especially over a public network. Here, we are providing the security for the input which is of 128 bits by using a key and it is encrypted at the transmission end and the same input is given at the receiver end which is finally decrypted to give the same input. This encryption and decryption blocks of the format AES-128 is efficiently performed by using VHDL. The secure transmission and reception of the data is then implemented on the FPGA kit for the purpose of checking it on a real time basis.

1.2 BLOCK DIAGRAM

Plain Text (128bits)

↓

←Round Key(0)

Sub Bytes

↓

Shift Rows

↓

Mix Columns

↓

← Round Key(0)

↓

Sub Bytes

↓

Shift Rows

↓

← Round Key(0)

↓

Cipher Text(128-b)

                                                                              

Cipher Text(128bits)

↓

←Round Key(Nr)

Inv Sub Bytes

↓

Inv Shift Rows

↓

Inv Mix Columns

↓

← Round Key(i)

↓

Inv   Sub Bytes

↓

Inv  Shift Rows

↓

← Round Key(0)

↓

Plain Text(128-bits)

 

Figure 1.1 Overview of AES Algorithm

 

1.3 TECHNICAL APPROACH

SOFTWARES

In this project, we are mainly using two soft wares to implement the project. They are:

• MODELSIM
• XILINX

 

XILINX: This tool can be used to create, implement, simulate, and synthesize HDL                designs for implementation on FPGA chips.

MODELSIM: This tool can be used to simulate HDL designs for implementation on FPGA chips.

 

HARDWARES

The hardware implementation of the project is done by using the SPARTAN 3E FPGA kit.

FPGA:

• FPGA stands for field-programmable gate array.
• A field-programmable gate array (FPGA) is an integrated circuit designed to be configured by a customer or a designer after manufacturing and hence “field programmable“.
• FPGAs contain an array of programmable logic blocks, and a hierarchy of reconfigurable interconnects that allow the blocks to be “wired together”, like many logic gates that can be inter-wired in different configuration.

1.4   PROJECT OVERVIEW

Chapter 1 includes the introduction, aim and block diagram which gives the information about the entire project. Chapter 2 consists about the references of other related IEEE projects that are related to our project. Chapter 3 briefly describes about the process of keeping the data secure by using encryption and decryption.  Chapter 4 emphasizes on the steps that are used to achieve the security using the AES algorithm. Chapter 5 focuses on the operations that are performed to implement the various parts of the algorithm.  Chapter 6 displays the software and hardware results of the project. Chapter 7 tells us about the advantages of the project and its various implementations. Chapter 8 concludes the project and gives us the idea about the extension of the project.

CHAPTER 2

LITERATURE SURVEY

Steganography is that the art of activity and transmission information through apparently innocuous carriers in a shot to hide the existence of the info, the word Steganography virtually means that coated or activity writing as derived from Greek. Steganography has its place in security. it’s not meant to interchange cryptography however supplement it.

Hiding a message with Steganography ways reduces the possibility of a message being detected. If the message is additionally encrypted then it provides another layer of protection. Therefore, some Steganographic ways mix ancient Cryptography with Steganography wherever sender encrypts the the secret message prior to the overall communication process, as it is more difficult for an attacker to detect embedded cipher text in a cover .

Security is playing a very important and crucial role in the field of network communication system and Internet. Data encryption standard (DES) is a private key cryptography system that provides the security in communication system but now a days the advancement in the computational power the DES seems to be weak against the brute force attacks. To improve the security of DES algorithm, the transposition technique is added before the DES algorithm to perform its process. By using an Enhanced DES algorithm the security has been improved which is very crucial in the communication and field of Internet. If the transposition technique is used before the original DES algorithm then the intruder required first to break the original DES algorithm and then transposition technique.

Triple DES was developed to handle obvious flaws in DES while not coming up with an entire new cryptosystem. Triple DES merely extends key size of DES by applying algorithmic rule thrice in succession with 3 totally different keys. The combined key size is so 168 bits (3 times 56), on the far side the reach of brute-force techniques like those employed by the get laid DES Cracker. Triple DES has continually been regarded with some suspicion, since the first algorithmic rule was ne’er designed to be utilized in this manner, however no serious flaws are uncovered in its style, and it’s these days accessible cryptosystem utilized in variety of net protocols.

Key growth generates a Key Schedule that’s employed in Cipher and Inverse Cipher procedures. The 128-bit plaintext and 128-bit key, also because the 128-bit output information were all divided into four 32-bit consecutive units severally controlled by the clock.

CHAPTER 3

INTRODUCTION TO CRYPTOGRAPHY

INTRODUCTION
Data which will be browse and understood with none special measures is named plaintext or clear text. the tactic of disguising plaintext in such how on hide its substance is named encoding. Encrypting plaintext leads toundecipherable hokum known as cipher text. you employ encoding to make sure that data is hidden from anyone for whom it’s not meant, even people who will see the encrypted knowledge. the method of reverting cipher text to its original plaintext is named decoding. Figure 3.1 illustrates this method.

The selection method to search out this new coding algorithmic program was absolutely receptive public scrutiny and comment; this ensured a radical, clear analysis of the styles. Fifteen competitive styles were subject to preliminary analysis by the planet cryptological community, as well as the National Security Agency (NSA). Its prospering use by the U.S. government semiconductor diode to widespread use within the non-public sector, leading AES to become the foremost standard algorithmic program utilized in trigonal key cryptography. AES is safer than its predecessors — DES and 3DES — because the algorithmic program is stronger and uses longer key lengths. It additionally allows quicker coding than DES and 3DES, creating it ideal for code applications, code and hardware that need either low-latency or high output, like firewall firmware and hardware that require either low-latency or high throughput, such as firewall and routers.

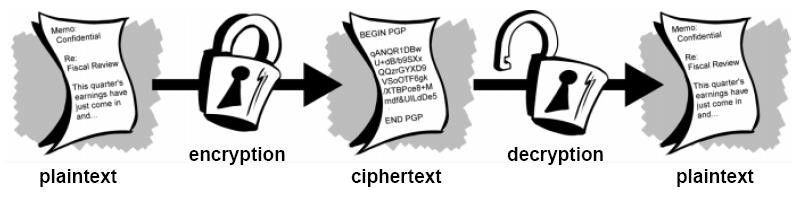
Figure 3.1 Encryption and Decryption

3.1.1 Cryptography

To enhance the protection of the info, code language for writing messages were used. The branch of arithmetic that investigates the code languages and strategies is termed cryptanalytics. cryptanalytics consists of 2 streams particularly cryptography and cryptology. Cryptography may be a science of committal to writing message on the QT whereas cryptology may be a science of breaking codes.
CRYPTOLOGY

CRYPTOGRAPHY cryptology

Our project cares with cryptography. Cryptography may be a science of victimisation arithmetic to cypher and decode information. Cryptography allows to store sensitive data or transmit it across insecure networks so it can not be browse by anyone except the meant recipient.

Cryptography or cryptanalytics comes from Greek kryptos “hidden” and also the verb grafo
“write” or legein “to speak” is that the follow and study of activity data. In contemporary world, cryptanalytics is taken into account to be a branch of each arithmetic and computing, and is afflicted closely with scientific theory, pc security and engineering. Cryptography is employed in applications gift in technology advanced in societies; examples embody the protection of the ATM cards, pc pass words and electronic commerce that all rely on Cryptography.

Cryptography strength is measured within the time and also the resources it might need to recover plain text. The results of the robust Cryptography is cipher text that’s terribly troublesome to decipher while not possession of the acceptable decipherment tool. however difficult? Given all today’s computing power and accessible time- even a billion computers doing a billion checks a second – it’s unimaginable to decipher the results of robust cryptography before the tip of the universe.

3.1.2 however will Cryptography Work

A cryptological algorithmic program, or cipher, may be a function utilized in the coding and secret writing method. A cryptological algorithmic program works together with a key—a word, number, or phrase—to cypher the plaintext. an equivalent plaintext encrypts to completely different |completely different} cipher text with different keys.

The security of encrypted information is entirely addicted to 2 things: the strength of the cryptological algorithmic program and also the secrecy of the key.

A scientific discipline formula, and all doable keys and every one the protocols that build it work comprise a cryptosystem. PGP may be a cryptosystem. Cryptosystem is divided in to package and Hardware.

CRYPTOSYSTEM

package HARDWARE

3.1.3 the aim of Cryptography

Cryptography is that the science of writing on the Q.T. code associated is an ancient art; the primary documented use of cryptography in writing dates back to circa 1900 B.C. once associate Egyptian scribe used non-standard hieroglyphs in associate inscription. Some specialists argue that cryptography appeared ad lib someday when writing was fictional, with applications starting from diplomatic missives to war-time battle plans. it’s no surprise, then, that new varieties of cryptography came presently when the widespread development of laptop communications.

In information and telecommunications, cryptography is critical once human activity over any un-trusted medium, which incorporates near to any network, significantly the web.

Within the context of any application-to-application communication, there area unit some specific security needs including:
• Authentication: the method of proving one’s identity. (The primary varieties of hostto-host authentication on the web these days area unit name-based or address-based, each of that area unit notoriously weak.)
• Privacy/confidentiality: making certain that nobody will scan the message except the meant receiver.
• Integrity: reassuring the receiver that the received message has not been altered in any means from the initial.
• Non-repudiation: A mechanism to prove that the sender very sent this message.

Cryptography, then, not solely protects information from thievery or alteration, however can even be used for user authentication. There are, in general, 3 varieties of scientific discipline schemes generally accustomed accomplish these goals: secret key (or symmetric) cryptography, public-key (or asymmetric) cryptography, and hash functions, every of that is delineated below. altogether cases, the initial unencrypted information is spoken as plaintext. it’s encrypted into cipher text, which can successively (usually) be decrypted into usable plaintext.

3.2 ways OF coding

Although there is many items to associate coding methodology, the 2 main items area unit the algorithms and therefore the keys. As explicit earlier, algorithms area unit typically complicated mathematical formulas that dictate the foundations of however the plaintext are going to be was cipher text. A secret’s a string of random bits that may be inserted into the formula. for 2 entities to be ready to communicate via coding, they have to use identical formula and, many times, identical key. In some coding ways, the receiver and therefore the sender use identical key and in alternative coding ways, they have to use completely different keys for coding and decipherment functions. the subsequent sections justify the distinction between these 2 varieties of codingways.

Symmetric Versus uneven Algorithms
Cryptography algorithms use either centrosymmetric keys, additionally known as secret keys, or uneven keys, additionally known as public keys. As coding wasn’t difficult enough, the titles that area unit accustomed describe the key type’s solely build it worse. simply pay shut attention and that we can get through this simply fine.

3.2.1 symmetric Cryptography

In a cryptosystem that uses centrosymmetric cryptography, each parties are going to be victimisation identical key for coding and decipherment, as shown in Figure three.2. This provides twin practicality. As we said, centrosymmetric keys also are known as secret keys as a result of this kind of coding depends on every user to stay the key a secret and properly protected. If this key got into associate intruder’s hand, that persona non grata would have the power to decode any intercepted message encrypted with this key.

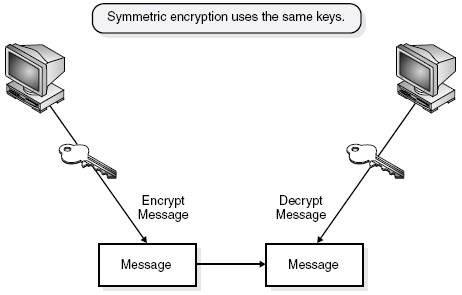
Figure 3.2 Using symmetric algorithms, the sender and receiver use the same key for encryption and decryption functions.

Figure 3.2 victimisation centrosymmetric algorithms, the sender and receiver use identical key for coding and decipherment functions.

The security of the centrosymmetric coding methodology is totally captivated with however well users defend the key. this could raise red flags to you if you’ve got ever had to depend upon an entire workers of individualsto stay a secret. If a secret’s compromised, then all messages encrypted therewith key is decrypted and browse by associate persona non grata.

The following list outlines the strengths and weakness of centrosymmetric key systems:
• Strengths
• Much quicker than uneven systems
• Hard to interrupt if employing a giant key size
• Weaknesses
• Key distribution: It needs a secure mechanism to deliver keys properly. • Scalability: every try of users desires a singular try of keys, that the range of • Keys grow exponentially.
• Limited security: It will give confidentiality, however not credibleness or nonrepudiation.

The following area unit samples of centrosymmetric key cryptography algorithms:
•Data coding normal (DES)
•Triple DES (3DES)
• Advanced coding normal (AES)

Paste your text here and click on “Next” to look at this text rewrite man do it’s issue.

haven’t any text to check? haven’t any text to check? Click “Select Samples”.3.2.2 uneven Cryptography
Some stuff you will tell the general public, however some stuff you simply wish to stay personal. In radial key cryptography, one secret key’s used between entities, whereas publicly key systems, every entity has completely different keys, or uneven keys. the 2 completely different uneven keys area unit mathematically connected. If a message is encrypted by one key, the opposite key’s needed to rewrite the message.

In a public key system, the combine of keys is formed from one public key and one personal key. the general public key may be familiar to everybody, and also the personal key should solely be familiar to the owner. Many times, public keys area unit listed in directories and informationbases of e-mail addresses in order that they area unit offered to anyone WHO needs to use these keys to encode or rewrite data once communication with a specific person. Figure 3.3 illustrates associate degree uneven cryptosystem.

Figure 3.3 uneven cryptosystem

The public and personal keys area unit mathematically connected, however can’t be derived from one another. this suggests that if associate degree wrongdoer gets a replica of Bob’s public key, it doesn’t mean he will currently use some mathematical magic and ascertain Bob’s personal key.

If confidentiality is that the most significant Security Service to a sender, she would encode the file with the receiver’s public key. {this is|this is often|this will be} referred to as a secure message format as a result of it can solely be decrypted by the one who has the corresponding personal key. If authentication is that the most significant Security Service to the sender, then she would encode the message along with her personal key. This provides assurance to the receiver that the sole {person WHO|one that|one who} might have encrypted the message is that the individual who has possession of that non-public key. If the sender encrypted the message with the receiver’s public key, authentication isn’t provided as a result of this public key’s offered to anyone.

Encrypting a message with the sender’s personal key’s referred to as associate degree open message format as a result of anyone with a replica of the corresponding public key will rewrite the message; so, confidentiality isn’t ensured.

For a message to be during a secure and signed format, the sender would encode the message along with herpersonal key and so encode it once more with the receiver’s public key. The receiver would then have to be compelled to rewrite the message together with his own personal key and so rewrite it once more with the sender’s public key. This provides confidentiality and authentication for that delivered message. the variouscryptography strategies area unit shown in Figure three.4.

Figure 3.4 style of Security Service which will be provided.

Each key kind may be accustomed encode and rewrite, thus don’t get confused and assume the general publickey’s just for cryptography and also the personal key’s just for secret writing. They each have the aptitude to encode and rewrite information.

The following outlines the strengths and weaknesses of uneven key systems:
• Strengths
• Better key distribution than radial systems
• Better measurability than radial systems
• Can give confidentiality, authentication, and non repudiation
• Weaknesses
• Works abundant slower than radial systems
The following area unit samples of uneven key algorithms:
• RSA
• Elliptic Curve Cryptosystem (ECC)
• Diffie-Hellman
• El Gamal
• Digital Signature commonplace (DSS)

3.3 forms of cryptanalytic ALGORITHMS

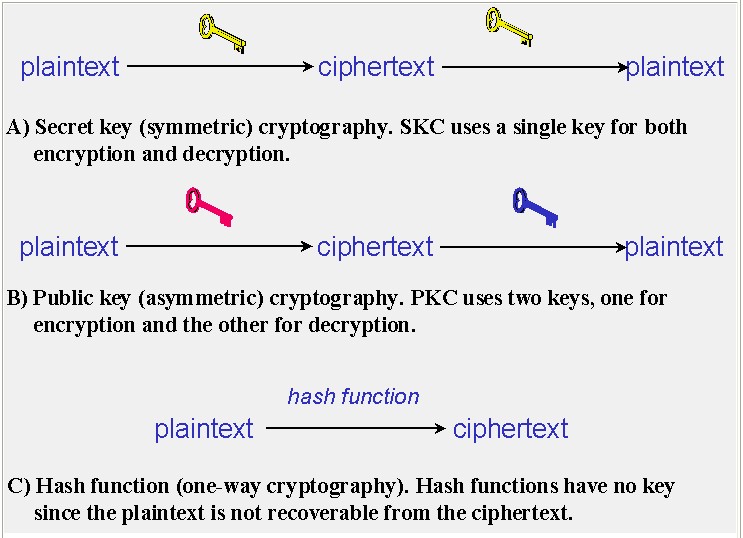
There area unit many ways that of classifying cryptanalytic algorithms. For functions of this paper, they’re going to be classified supported the amount of keys that area unit utilized for cryptography and secret writing, and more outlined by their application and use. The 3 forms of algorithms those area unit mentioned in Figure three.5.

• Secret Key Cryptography (SKC): Uses one key for each cryptography and secret writing
• Public Key Cryptography (PKC): Uses one key for cryptography and another for secret writing
• Hash Functions: Uses a mathematical transformation to irreversibly “encrypt” info

« Back Rewrite again Next »

Figure 3.5 3 styles of science algorithms

3.4  INTRODUCTION AES

The Advanced coding customary (AES) specifies a FIPS-approved science algorithmic rule which will be accustomed shield electronic knowledge. AES algorithmic rule may be a bilaterally symmetric block cipher which will encode (encipher) and decipher (decipher) info. coding converts knowledge to associate unintelligible kind known as cipher-text; decrypting the cipher-text converts the information back to its original kind, known as plaintext.

Figure 3.6 Overall Representations of coding and decoding

The Rijndael, whose name relies on the names of its 2 Belgian inventors, Joan Daemen and Vincent Rijmen may be a Block cipher, which suggests that it works on mounted length cluster of bits, that ar known as blocks. It takes associate input block of a definite size, sometimes 128 bits, and produces a corresponding output block of constant size. that may be a series of mathematical operations that use substitutions (also known as S-Box) and permutations (P-Boxes) and their careful definition implies each} output bit depends on every input bit.

3.4.1 Block Cipher

When a block cipher algorithmic rule is employed for coding and decoding functions, the message is split into blocks of bits. These blocks ar then place through substitution, transposition, and different mathematical functions.

The algorithmic rule dictates all the potential functions offered to be used on the message, and it’s the key can| which will| that may} verify what order these functions will happen. robust algorithms build reengineering or attempting to work out all the functions that came about on the message, primarily not possible.

CHAPTER 4

ADVANCED ENCRYPTION STANDARD ALGORITHM

4.1 INTRODUCTION

The main objectives of AES ar high level security, adoptable to numerous application, economical and marketable. during this project work, the plain text of 128 bits is given as input to cryptography block within whichcryptography of information is formed and therefore the cipher text of 128 bits is throughout as output. The key length of 128 bits is employed in method of cryptography. The AES formula may be a block cipher that uses constant binary key each to write in code and decipher knowledge blocks is termed a centrosymmetric key cipher. A normally accepted definition of an honest centrosymmetric key formula, like the AES, is that there exists no attack higher than key exhaustion to scan associate degree encrypted message.

4.2 TERMINOLOGIES

the assorted terminologies and their definitions employed in this project were mentioned during this section.

S.No.	Term	Definition
1	AES	Advanced Encryption Standard
2	Array	An enumerated collection of identical entities (e.g., an array of bytes).
3	Bit	A binary digit having a value of 0 or 1.
4	Block	Sequence of binary bits that comprise the input, output, State and Round Key. The length of a sequence is the number of bits it contains. Blocks are also interpreted as arrays of bytes.
5	Byte	A group of eight bits that is treated either as a single entity or as an array of 8 individual bits.
6	Cipher	Series of transformations that converts plaintext to cipher text using the Cipher Key.
7	Cipher Key	Secret, cryptographic key that is used by the Key   Expansion routine to generate a set of Round Keys; can
		be pictured as a rectangular array of bytes, having four rows and Nk columns.
8	Cipher text	Data output from the Cipher or input to the Inverse Cipher.
9	Inverse Cipher	Series of transformations that converts cipher text to plaintext using the Cipher Key.
10	Key Expansion	Routine used to generate a series of Round Keys from the Cipher Key.
11	Plaintext	Data input to Cipher or output from the Inverse Cipher.
12	Rijndael	Cryptographic algorithm specified in this Advanced Encryption Standard (AES).
13	Round Key	Round keys are values derived from the Cipher Key using the Key Expansion routine; they are applied to the State in the Cipher and Inverse Cipher.
14	State	Intermediate Cipher result that can be pictured as a rectangular array of bytes, having four rows and Nb columns.
15	S-box	Non-linear substitution table used in several byte substitution transformations and in the Key Expansion routine to perform a one-for-one substitution of a byte value.
16	Word	A group of 32 bits that is treated either as a single entity or as an array of 4 bytes.

 

Table 4.1 Terminologies and their Definitions

4.3 ALGORITHM PARAMETERS

The different parameters and symbols used in this project were discussed in this section.

S.No.	Parameters &   Symbols	Definition
1	AddRoundKey	Transformation in the Cipher and Inverse Cipher in which a Round Key is added to the State using an XOR operation. The length of a Round Key equals the size of
		the State (i.e., for Nb = 4, the Round Key length equals 128 bits/16 bytes).
2	InvMixColumns	Transformation in the Inverse Cipher that is the inverse of MixColumns.
3	InvShiftRows	Transformation in the Inverse Cipher that is the inverse of ShiftRows.
4	InvSubBytes	Transformation in the Inverse Cipher that is the inverse of SubBytes.
5	K	Cipher Key.
6	MixColumns	Transformation in the Cipher that takes all of the columns of the State and mixes their data (independently of one another) to produce new columns.
7	Nb	Number of columns (32-bit words) comprising the State.   For this standard, Nb= 4.
8	Nk	Number of 32-bit words comprising the Cipher Key. For this standard, Nk = 4.
9	Nr	Number of rounds, which is a function of Nk and Nb(which is fixed). For this standard, Nr= 10.
10	Rcon	The round constant word array.
11	RotWord	Function used in the Key Expansion routine that takes a four-byte word and performs a cyclic permutation.
12	ShiftRows	Transformation in the Cipher that processes the State by cyclically shifting the last three rows of the State by different offsets.
13	SubBytes	Transformation in the Cipher that processes the State using a nonlinear byte substitution table (S-box) that operates on each of the State bytes independently.
14	SubWord	Function used in the Key Expansion routine that takes a four-byte input word and applies an S-box to each of the four bytes to produce an output word.
15	XOR	Exclusive-OR operation.

 

Table 4.2 Parameters, Symbols and their Definitions

4.4 AES algorithmic program

The AES is AN iterated stellate block cipher, which implies that, • AES works by repetition an equivalent outlined steps multiple times.
• AES could be a secret key secret writing algorithmic program.
• AES operates on a hard and fast range of bytes.

AES likewise as most secret writing algorithms is reversible. this suggests that just about an equivalent steps ar performed to complete each secret writing and decipherment in reverse order. The AES algorithmic program operates on bytes, that makes it less complicated to implement.

4.4.1 Specification

For the AES algorithmic program, the length of the input block, the output block and also the State is 128 bits. this can be delineated by Nb = four, that reflects the amount of 32-bit words (number of columns) within the State. For the AES algorithmic program, the length of the Cipher Key, K, is 128 bits. The key length is delineated by Nk = four, that reflects the amount of 32-bit words (number of columns) within the Cipher Key.

For the AES algorithmic program, the amount of rounds to be performed throughout the execution of the algorithmic program relies on the key size. the amount of rounds is delineated by Nr, wherever Nr = ten once Nk = four.

4.4.2 Description

The AES is AN iterated block cipher with a hard and fast block size of 128 and a variable key length. the various transformations care for the intermediate results, referred to as state. The state could be a rectangular array of bytes and since the block size is 128 bits, that is sixteen bytes, the oblong array is of dimensions 4×4. the essential unit for process within the AES algorithmic program could be a computer memory unit, a sequence of eight bits treated as one entity. The input, output and Cipher Key bit sequences that ar processed as arrays of bytes that arfashioned by dividing these sequences into teams of eight contiguous In the Rijndael version with variable block size, the row size is fastened to four and also the range of columns varies. the amount of columns is that the block size divided by thirty two and denoted Nb. The cipher secret’s equally pictured as an oblong array with four rows. the amount of columns of the cipher key, denoted Nk, is capable the key length divided by thirty two. AES uses a variable range of rounds, that ar fixed: A key of size 128 has ten rounds.

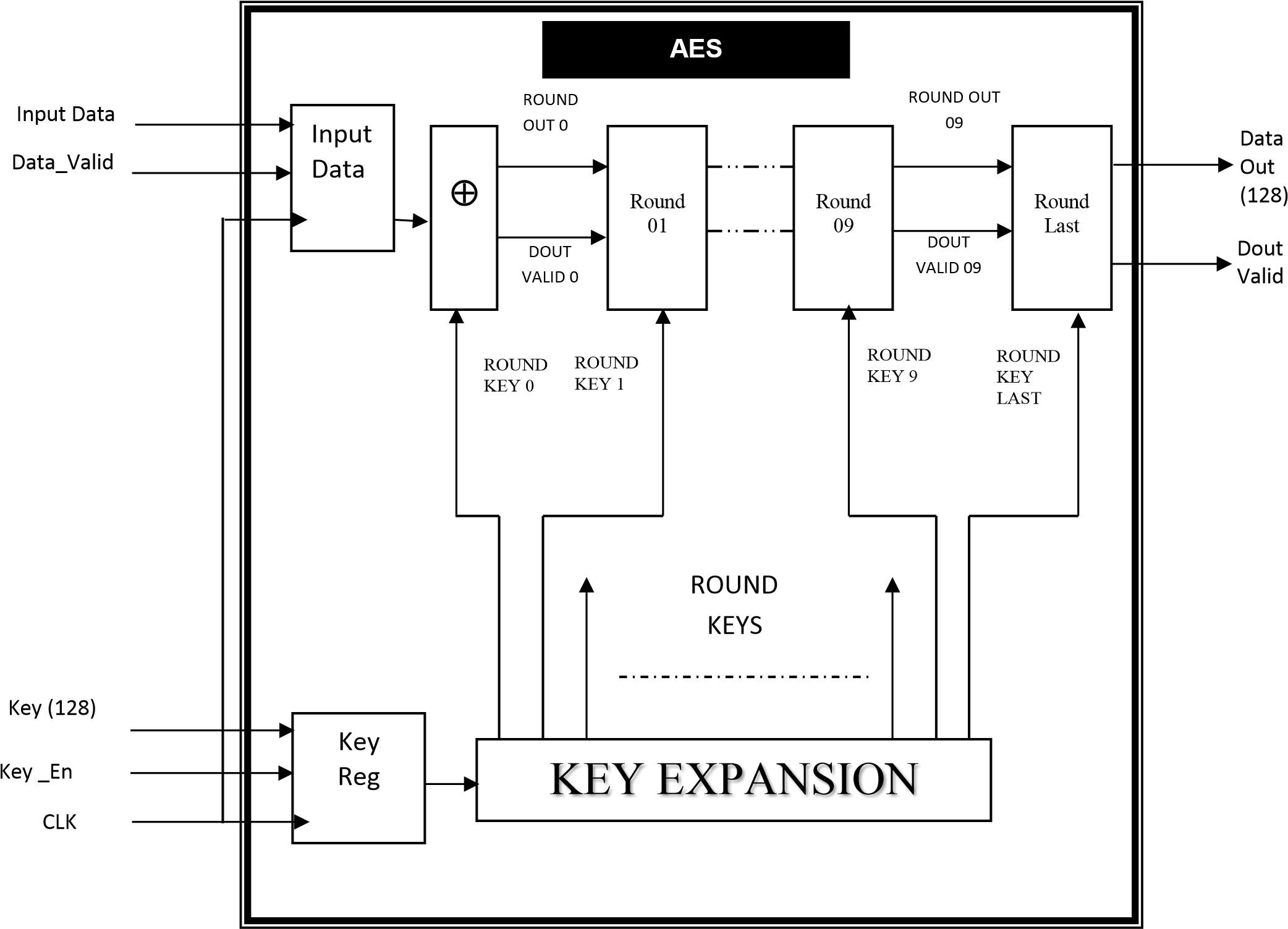
Figure 4.1 Top Level Block Diagram of AES Algorithm

Paste your text here and click on “Next” to look at this text redact do it’s issue.

don’t have any text to check? don’t have any text to check? Click “Select Samples”.Figure 4.1 prime Level diagram of AES algorithmic rule 

The on top of figure five.1 shows the highest level blocks obtainable within the AES algorithmic rule. conjointlythe fundamental inputs to the system and therefore the outputs from the system were clearly described. As per the quality, ten sphericals for 128 bits key length were administered during which the last round are going to be performed individually. For each its Cipher and Inverse Cipher, the AES algorithmic rule uses a spherical operatethat’s composed of 4 completely different byte-oriented transformations:
• Byte substitution employing a substitution table (S-box).
• Shifting rows of the State array by completely different offsets.
• Mixing the info inside every column of the State array.
• Adding a spherical Key to the State.

4.5 coding

At the beginning of the coding or Cipher, the input file and therefore the input key were derived to the State array mistreatment the conventions. ab initio the XOR operation ought to be performed between every computer memory unit of the input file and therefore the input key and therefore the output are going to be given because the input of the Round-1. when AN initial spherical Key addition, the State array is reworked by implementing a spherical operate ten times, with the ultimate spherical differing slightly from the primary Nr–1 rounds. the ultimate State is then derived to the output. The spherical operate is parameterized employing a key schedule that consists of a one-dimensional array of four-byte words derived mistreatment the Key enlargement routine.

The individual transformations that administered area unit listed below.
• SubBytes
• ShiftRows
• MixColumns
• AddRoundKey

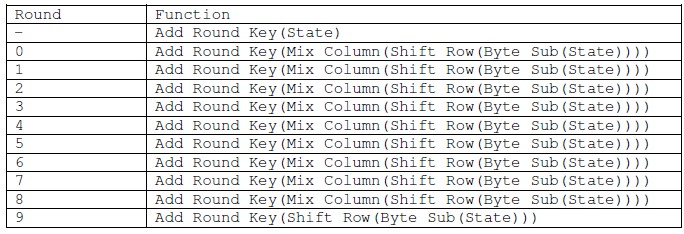
Table 5.3 AES encryption cipher using a 16 byte key

Table 5.3 AES coding cipher employing a sixteen computer memory unit key

Table 5.3 represents the operation performed at every spherical and its order during which all is administered. All Nr (Number of sphericals) rounds area unit identical with the exception of the ultimate round, that doesn’tembrace the combo Columns transformation. so the cipher text, that is, encrypted information are going to be achieved at the tip of the ultimate spherical.

4.5.1 AES Cipher Functions

The diagram shown within the figure five.2 represents the functions administered in every spherical and therefore the functions performed within the last spherical.

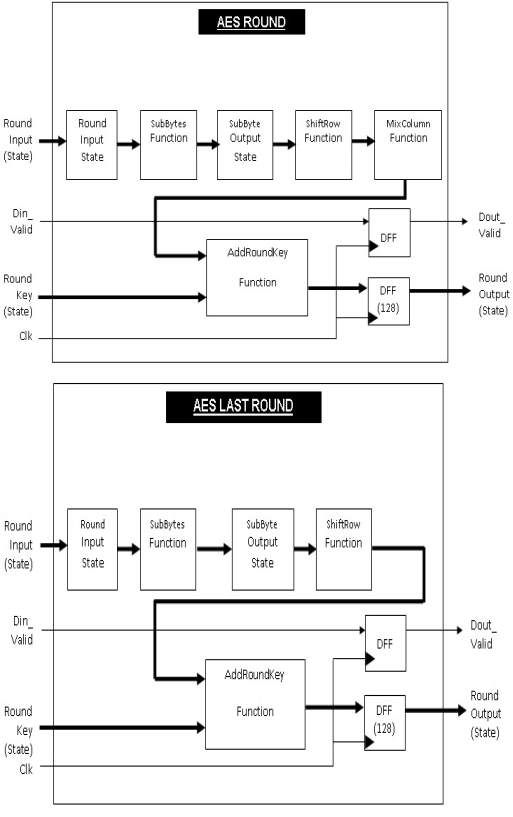Figure 4.2 Figure 4.2 Diagram for AES Round and AES Last Round

4.5.1.1 Sub Bytes Transformation

The Sub Bytes operation could be a non-linear computer memory unit substitution, operative on every computer memory unit of the state severally. The substitution table (S-Box) is invertible and is made by the composition of 2 transformations:
• Take the inverse in Rijndael’s finite field • Apply associate degree transformation.

Since the S-Box is freelance of any input, pre-calculated forms square measure used, if enough memory (256 bytes for one S-Box) is offered. every computer memory unit of the state is then substituted by the worth within the S-Box whose index corresponds to the worth within the state. Figure 5.3 illustrates the impact of the SubBytes transformation on the State clearly

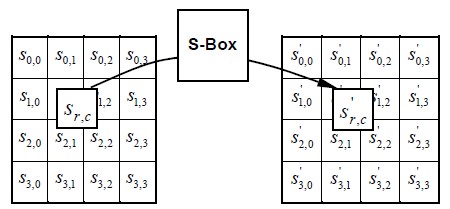
                 Figure 4.3 Sub Bytes Operation of the State

Figure 4.3 Sub Bytes Operation of the State

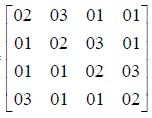
The S-Box for the coding is given within the Appendix-1 for the reference. The S-Box are going to be of a 16X16 matrix within which the row is described as “x” and also the column is described by “y”. The S-box employed in the Sub Bytes transformation is given in hex kind and therefore the substitution worth would be determined by the intersection of the row and also the column.

For example, if S1,1 = , then the substitution worth would be determined by the intersection of the row with index ‘5’ and also the column with index ‘3’. this might end in S1,1 having a worth of . These values are often referred within the S-Box gift within the Appendix.

4.5.1.2 Shift Rows Transformation

Arranges the state during a matrix and so performs a circular shift for every row. this can be not a trifle wise shift. The circular shift simply moves every computer memory unit one area over. A computer memory unit that was within the second position could find yourself within the third position when the shift.

The circular a part of it specifies that the computer memory unit within the last position shifted one area can find yourself within the initial position within the same row. therefore during this Shift Rows operation, every row of the state is cyclically shifted to the left, looking on the row index. This has the impact of moving bytes to “lower” positions within the row, whereas the “lowest” bytes wrap around into the “top” of the row.

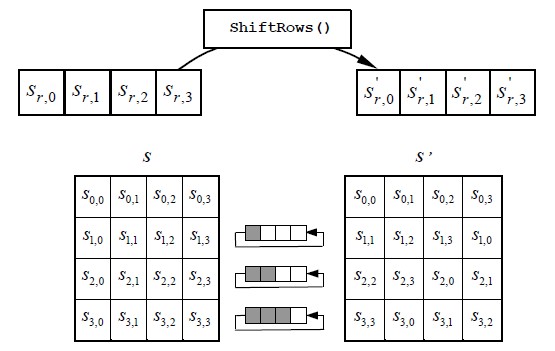
                                      Figure 5.4 ShiftRows Operation of the State

Figure 5.4 illustrates the Shift Rows transformation. The shifting operation are going to

Figure 5.4 illustrates the Shift Rows transformation. The shifting operation are going to be disbursed horizontally as follows.
• The first row is shifted zero positions to the left.
• The ordinal row is shifted one positions to the left.
• The third row is shifted two positions to the left.
• The fourth row is shifted three positions to the left.

4.5.1.3 combine ColumnsTransformation

In combine Columns operation, elements of the state square measure increased against that elements of the matrix. The transformation operates on the State column-by-column. The take is organized into a four row table (as delineated within the Shift Row function). The multiplication is performed one column at a time (4 bytes). everyworth within the column is eventually increased against each worth of the matrix (16 total multiplications). The results of those multiplications square measure XORed along to provide solely four result bytes for future state. so four bytes input, sixteen multiplications twelve XORs and four bytes output. The multiplication is performed one matrix row at a time against every worth of a state column.

The pre-defined 4X4 matrix worth and also the initial column of the ShiftRows state square measure described as follows, for the multi

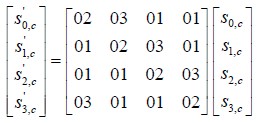
The first result computer memory unit is calculated by multiplying four values of the state column against four values of the primary row of the matrix. The results of every multiplication is then XORed to provide one computer memory unit.

The second result computer memory unit is calculated by multiplying identical four values of the state column against four values of the second row of the matrix. The results of every multiplication is then XORed to provideone computer memory unit.

The third result computer memory unit is calculated by multiplying identical four values of the state column against four values of the third row of the matrix. The results of every multiplication is then XORed to provide onecomputer memory unit.

The fourth result computer memory unit is calculated by multiplying identical four values of the state column against four values of the fourth row of the matrix. The results of every multiplication is then XORed to provide one computer memory unit.

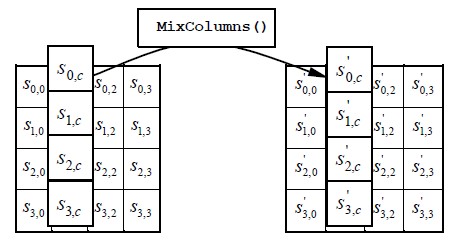
        Figure 5.6 MixColumns operates on the State column-by-column

This procedure is perennial once more with future column of the state, till there aren’t any additional state columns. There fore swing it all at once, the primary column can embody state bytes 1-4 and can be increased against the matrix within the following manner:

Paste your text here and click on “Next” to observe this text editor do it’s issue.

don’t have any text to check? don’t have any text to check? Click “Select Samples”.
Figure 5.5 Illustrates the MixColumns transformation

Figure 5.6 MixColumns operates on the State column-by-column

Hence the representation of the MixColumns operation diagrammatical higher than provides the clear read on this transformation.

5.1.4 Add spherical Key Transformation

In the Add spherical Key Transformation, a spherical secret’s adscititious to the State by an easy bitwise XOR operation. every of the sixteen bytes of the state is XORed against every of the sixteen bytes of some of the expanded key for this spherical. The expanded Key bytes ar ne’er reused. thus once the primary sixteen bytes ar XORed once morest the primary sixteen bytes of the expanded key then the expanded key bytes 1-16 ar ne’er used again. succeeding time the Add spherical Key perform is termed bytes 17-32 ar XORed against the state.

The first time Add spherical Key gets dead.

The second time Add spherical secret’s dead.

This method are continued till the operation ends. The graphical illustration of this operation will be seen below.

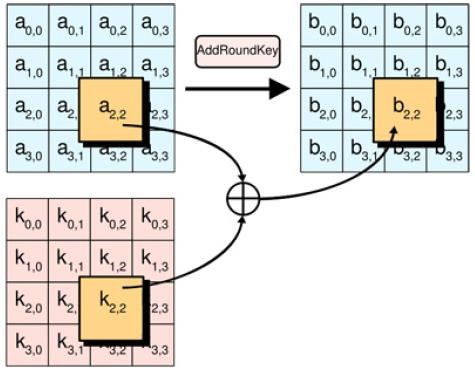
Figure 5.7 Add Round Key Operation

Figure 5.7 Add spherical Key Operation

The higher than figure five.7 represents the clear read on the Add spherical Key transformation that takes place between the results of combine Columns and Key enlargement and provides the resultant matrix that’s used because the input to succeeding spherical.

4.5.2 Key enlargement

before encoding or cryptography the key should be expanded . The expanded secret’s employed in the Add spherical Key perform outlined higher than. every time the Add spherical Key perform is termed a special a part of the expanded secret’s XORed against the state. so as for this to figure the expanded Key should be massive enough so it will offer key material for each time the Add spherical Key perform is dead. The Add spherical Key perform gets involved every spherical also mutually time beyond regulation at starting of the algorithmic program.

The AES algorithmic program takes the Cipher Key, K, and performs a Key enlargement routine to get a key schedule. The Key enlargement generates a complete of Nb (Nr + 1) words: the algorithmic program needsassociate initial set of Nb words, and every of the Nr rounds needs Nb words of key knowledge. The ensuing key schedule consists of a linear array of 4-byte words.

There is a relation between the cipher key size, the amount of rounds and therefore the expanded Key size. For associate 128-bit key, there’s one initial Add spherical Key operation and there ar ten sphericals and every round wants a replacement sixteen computer memory unit key, thus we tend to need 10+1 spherical Keys of sixteencomputer memory unit, that equals 176 computer memory unit. associate iteration of the higher than steps is termed a spherical. the quantity of rounds of the key enlargement algorithmic program depends on the key size.

Table 5.4 Key Expansion

Table 5.4 Key enlargement

The key enlargement routine executes a most of four consecutive functions. These functions are:
• ROT WORD
• SUB WORD
• RCON
• XOR

Rot Word (4 bytes)
This will a circular shift on four bytes the same as the Shift Row perform. The 4-byte word is cyclically shifted onecomputer memory unit to the left.
For Example, let’s take a sequence one,2,3,4 which is able to be revolved and acquire the result as a pair of,3,4,1

Sub Word (4 bytes)
The Key Schedule uses identical S-Box substitution because the main algorithmic program body. This step applies the S-box worth substitution as represented in SubBytes perform to every of the four bytes within the argument. The S-Box is gift within the Appendix-1 for the reference.

Basically this function returns a 4 byte value based on the following table.

Round Number	Rcon
1	Rcon(1)	01000000
2	Rcon(2)	02000000
3	Rcon(3)	04000000
4	Rcon(4)	08000000
5	Rcon(5)	10000000
6	Rcon(6)	20000000
7	Rcon(7)	40000000
8	Rcon(8)	80000000
9	Rcon(9)	1B000000
10	Rcon(10)	36000000

 

Table 5.5 Rcon Table

The results of the Sub Words ought to be XORed with the higher than mentioned Rcon values with relevancy the corresponding spherical variety. It will be seen that the primary Nk words of the expanded key ar full of the Cipher Key. each following word, w[i], is adequate to the XOR of the previous word, w[i-1], and therefore the word Nk positions earlier, w[i-Nk]. For words in positions that ar a multiple of Nk, a change is applied to w[i-1] before the XOR, followed by associate XOR with a spherical constant, Rcon[i].
Steps in Key enlargement
• The initial n bytes of the expanded key ar merely the cipher key (n = the scale of the encoding key)
• The rcon worth i is about to one
• Until we’ve got enough bytes of expanded key, we tend to do the subsequent to get n additional bytes of expanded key (please note another time that “n” is employed here, this varies looking on the key size)
1. we tend to do the subsequent to get four bytes
we use a brief 4-byte word referred to as t
we assign the previous four bytes to t
we perform the key schedule core on t, with i as Rcon worth
we increment i
we XOR t with the 4-byte word n bytes before within the expanded key
(where n is once sixteen bytes)
2. we tend to do the subsequent x times to get succeeding x*4 bytes of the expanded key (x = three for n=16)
we assign the previous 4-byte word to t
we XOR t with the 4-byte word n bytes before within the expanded key (where n is once sixteen bytes)
Hence, for n=16, we tend to generate: four + 3*4 bytes = sixteen bytes per iteration.

4.6 cryptography

The cipher text of 128 bits and therefore the same key of 128 bits are given because the input to the cryptography block. The encrypted knowledge are decrypted and therefore the original plain message are achieved because the output of the cryptography block. The Cipher transformations will be inverted and so enforced in reverse order to supply an easy Inverse Cipher for the AES algorithmic program. The individual transformations employed in the Inverse Cipher were listed as follows.
• Inv Shift Rows
• Inv Sub Bytes
• Inv combine Columns • Add spherical Key

Here conjointly ten sphericals are dole out and therefore the solely distinction within the cryptography block with relevancy the algorithmic program flow is that the results of the Key enlargement of every round also willincline to the combo Columns operation when that the Add spherical Key transformation ought to be dole out.
Inv combine Columns (state XOR spherical Key) = Inv combine Columns (state) XOR Inv combine Columns (Round Key)

The higher than equation represents the essential distinction within the method of the AES encoding and cryptography algorithmic program.

How Does The Article Rewriter Tool Work?

4.6.1 AES Inverse Cipher Functions
The AES Inverse Cipher perform has an equivalent set of transformations as within the coding however within the inverse type, that is, the predefined values that used for the every transformation are completely different. during this section we are able to discuss regarding every transformations intimately.

4.6.1.1 Inv Sub Bytes Transformation
Inv Sub Bytes is that the inverse of the computer memory unit substitution transformation, during which the inverse S-Box is applied to every computer memory unit of the State. The inverse S-Box is gift within the Appendix-1 for the reference. The transformation of this method are applied within the similar approach as within the Sub Bytes within the coding like the substitution price would be determined by the intersection of the row and therefore the column.

For example, if S1,1 = , then the substitution price would be determined by the intersection of the row with index ‘5’ and therefore the column with index ‘3’. this may end in S1,1 having a price of . These values are often referred within the S-Box gift within the Appendix-1.

4.6.1.2 Inv Shift Rows Transformation
The Inv Shift Rows is that the inverse of the Shift Rows transformation. The bytes within the last 3 rows of the State area unit cyclically shifted over completely different numbers of bytes (offsets). the primary row, r = 0, isn’t shifted. the lowest 3 rows area unit cyclically shifted by Nb – shift(r,Nb) bytes, wherever the shift price shift(r,Nb) depends on the row variety. Specifically, the Inv Shift Rows transformation income as follows.

Figure 5.8 Inv Shift Rows Operation of the State

4.6.1.3 Inv combine Columns Transformation
The Inv combine Columns is that the inverse of the combo Columns transformation. Inv combine Columns operates on the State considering column-by-column. The pre-defined 4X4 matrix price and therefore the initial column of the Inv Shift Rows state area unit described as follows, for the multiplication.

As a results of this multiplication, the four bytes during a column area unit replaced by the subsequent.

therefore the 4X4 matrix are obtained which is able to run because the input to following transformation.

4.6.1.4 Inverse of the Add spherical Key Transformation
The Inverse of the Add spherical key’s like the Add spherical Key within the coding method. every part within the resultant matrix of combine Columns and resultant matrix of Key enlargement are XORed and therefore the resultant matrix of Add spherical Key are given because the input to following spherical.

therefore all the inverse cipher transformations were mentioned higher than and at last, the sole issue left to try to to is golf shot it all at once in one inversed main algorithmic rule. equally the forward cipher transformations were combined along to create a spherical and mixing all the ten Rounds can represent a whole AES coding and decipherment algorithmic rule.

CHAPTER  5

AES ALGORITHM IMPLEMENTATION

5.1 INTRODUCTION

The AES may be a block cipher. this implies that the amount of bytes that it encrypts is fastened. AES willpresently code blocks of sixteen bytes at a time; no alternative block sizes area unit presently a vicinity of the AES normal. If the bytes being encrypted area unit larger than the required block then AES is dead at the same time. This additionally means AES needs to code a minimum of sixteen bytes. If the plain text is smaller than sixteen bytes then it should be soft. merely aforementioned the block may be a relation to the bytes that area unit processed by the formula.

5.2 IMPLEMENTATION

throughout the implementation, there area unit totally different parameters area unit needed that area unitmentioned as follows.

Input Data Length needs
An implementation of the AES formula ought to have the input file (Plain Text) length of 128 bits that acts because the primary input to the each secret writing and decipherment block.

Key Length needs
In this AES implementation the input key chosen to be as 128 bits from the assorted key lengths out there. This additionally acts because the primary input to the each secret writing and decipherment block.

Keying Restrictions
No weak or semi-weak keys are known for the AES formula and there’s no restriction on key choice.

Parameterization of Block Size and spherical variety
Here since the input file and also the input key lengths area unit 128 bits, the block size are of Nb = four and also the spherical variety are of Nr = ten. The spherical variety are enamored relevance the AES formula normal.

6.3 NOTATION AND CONVENTIONS 
the various notations and conventions were employed in this implementation of AES formula.

HEX 
Hexadecimal defines a notation of numbers in base sixteen. This merely means the best variety which will be diagrammatic in an exceedingly single digit is fifteen, instead of the standard nine within the decimal (base 10) system. thus all the values were diagrammatic within the hex system of numeration.

Inputs and Outputs
The input and output for the AES formula every incorporates sequences of 128 bits (digits with values of zero or 1). These sequences can generally be brought up as blocks and also the variety of bits they contain are brought up as their length. The Cipher Key for the AES formula may be a sequence of 128 bits. alternative input and output lengths aren’t allowable by this normal.

Bytes 
The basic unit for process within the AES formula may be a computer memory unit, a sequence of eight bits treated as one entity. The input, output and Cipher Key bit sequences area unit processed as arrays of bytes that area unit fashioned by dividing these sequences into teams of eight contiguous bits to make arrays of bytes. For associate input, output or Cipher Key denoted by a, the bytes within the ensuing array are documentedexploitation one in every of the 2 forms, “an” or a[n], wherever n are in one in every of the subsequent ranges.
• Key length = 128 bits, zero ≤ n < sixteen
• Block length = 128 bits, zero ≤n < sixteen
State 
Internally, the AES algorithm’s operations area unit performed on a two-dimensional array of bytes referred to as the State. The State consists of 4 rows of bytes, every containing Nb bytes, wherever Nb is that the block length divided by thirty two. within the State array denoted by the image s, every individual computer memory unit has 2 indices, with its row variety r within the vary zero ≤ r < four and its column variety c within the vary zero ≤ c < Nb. this permits a personal computer memory unit of the State to be brought up as either sr,c or s[r,c]. For this normal, Nb =4, i.e., zero ≤ c < four.

At the beginning of the Cipher and Inverse Cipher, the input (the array of bytes in0, in1, … in15) are traced into the State array. The Cipher or Inverse Cipher operations area unit then conducted on this State array, once that its final price is traced to the output are the array of bytes out0, out1, … out15.

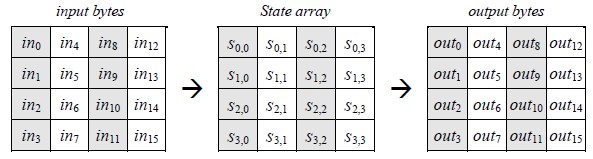
Figure 6.1 State Array Input and Output

Figure 6.1 State Array Input and Output

Hence, at the start of the Cipher or Inverse Cipher, the input array, in, is traced to the State array per the scheme:

S [r, c] = in[r + fourc] for zero ≤ r < 4 and zero ≤ c < Nb.

And at the tip of the Cipher and Inverse Cipher, the State is traced to the output array out as follows:
Out [r + 4c] = s[r, c] for zero ≤ r < four and zero ≤ c < Nb.

State as associate Array of Columns
The four bytes in every column of the State array kind 32-bit words, wherever the row variety r provides associate index for the four bytes inside every word. The state will thus be understood as a one-dimensional array of thirty two bit words (columns), w0…w3, wherever the column variety c provides associate index into this array. thus the State will be thought of as associate array of 4 words, as follows:
w0 = s0,0 s1,0 s2,0 s3,0 w2 = s0,2 s1,2 s2,2 s3,2 w1 = s0,1 s1,1 s2,1 s3,1 w3 = s0,3 s1,3 s2,3 s3,3

5.4 MATHEMATICAL PRELIMINARIES
All bytes within the AES formula area unit understood as finite field components which will be value-added and increased, however these operations area unit totally different from those used for numbers.

Addition
The addition of 2 parts during a finite field is achieved by “adding” the coefficients for the corresponding powers within the polynomials for the 2 parts. The addition is performed with the XOR operation (denoted by ). as an example, 2 hex numbers are taken and also the addition, that is, XOR operation has performed.
 = Multiplication
The standard product of a(x) and b(x), denoted by a(x)  b(x), is given by d(x) that ar given as follow.
The matrix of 4X4 is taken and is increased with the one column, that is, matrix operation must be performed.
The multiplication of the on top of matrix is performed within the following manner.

 

5.5 GENERAL IMPLEMENTATION FLOW

The generalized implementation flow sheet of the project is delineate as follows.

Figure 6.2 General Implementation flow sheet

Once the useful verification is evident, the RTL model are going to be taken to the synthesis method. 3 operations are going to be disbursed within the synthesis method like
• Translate
• Map
• Place and Route

The developed RTL model are going to be translated to the mathematical equation format which can be within theintelligible format of the tool. These translated equations are going to be then mapped to the library that’s, mapped to the hardware. Once the mapping is completed, the gates were placed and routed. Before these processes, the constraints is given so as to optimize the planning. Finally the BIT MAP file are going to be generated that has the planning info within the binary format which can be drop within the FPGA board.

5.6IMPLEMENTATION

The project deals with each the secret writing and coding algorithmic program and its operation.

RTLModelling
• The implementation of the secret writing and coding ought to be differentiated and also the system shouldunderstand that one it ought to perform. therefore a proof “Enc_Dec” is asserted which can represents the operation of the system, that is, system is either in secret writing or coding.
• The given computer file and key are going to be regenerate to a State and Word for the any transformation.
• For accessing the State, that is, 4X4 array, 2 loops are used with the naming convention of ‘i’ and ‘j’.

Key growth
• The implementation of AES with the Cipher Key growth, that’s to enlarge our input cipher key, whose size is 128 bits into a bigger key, from that completely different spherical Keys is derived.
• From the theoretical half, it’s renowned already that Rotate takes a word (a 4-byte array) and rotates it eight bit to the left. Since eight bit correspond to 1 computer memory unit and also the array kind is character (whose size is one byte), rotating eight bit to the left corresponds to shifting cyclically the array values one to the left.
• The implementation of Rcon is completed with reference to the counter. The counter is about with reference tospherical variety and also the Rcon worth are going to be calculated by playacting the multiplication operation between the input worth and constant worth.
• The Key growth is wherever it all comes along. As you’ll see within the pretty huge list within the theory concerning the Rijndael Key growth, we’d like to use many operations variety of times, betting on they key size. Key growth perform essentially wants solely 2 things:
• Input cipher key
• Output enlarged key
• All the operations ought to be applied one when the opposite on the 4-byte word that will the whole operation. The parameters ar the 4-byte word and also the iteration counter,
on that Rcon depends. therefore this Key growth are going to be calculated and every sixteen bytes are going to be given to every spherical.

AES secret writing
• To implement the AES secret writing algorithmic program, we have a tendency to proceed precisely the same approach as for the key growth, that is, we have a tendency to 1st implement the essential helper functions so move up to the most loop. The functions take as parameter a state, which is, as already explained, an oblong 4×4 array of bytes.
• The Shift Rows perform iterates over all the rows so calls shift Row with the proper offset. Shift Row will nothing however to shift a 4-byte array by the given offset.
• This is that the half that involves the spherical Key was generated throughout every iteration. Here merely XOR every computer memory unit of the key to the several computer memory unit of the state
• The combine Columns implementation was disbursed by 1st one would generate a column so decision combine Column, which might then apply the matrix operation.
• As you’ll see within the theory, one AES spherical is that the one that must apply all four operations on the state consecutively. All we’ve got to try to to is take the state, the enlarged Key and also the variety of rounds as parameters so decision the operations one when the opposite.

AES coding
• For the AES coding, the key schedule stays a similar, the sole operations we’d like to implement ar the inversed Sub Bytes, Shift Rows and blend Columns, whereas Add spherical Key stays a similar.
• As you’ll see, they’re nearly the image of their secret writing except that the rotation this point is to the correctwhich we have a tendency to use the inversed S-Box for the substitution. As for the Inversed combine Columns operation, the sole distinction is that the multiplication matrix is completely different.
• Finally, the sole issue left to try to to is putt it all at once in one inversed main algorithmic program. Please note that we have a tendency to use our enlarged key backwards, beginning with the last sixteen bytes so moving towards the beginning.
• The separate modules were written for the Last spherical and alternative Rounds. From 1st spherical to ninth around the same module is instantiated and for the last spherical, a separate module was used since it doesn’t have the combination Columns operation.

CHAPTER 6

RESULTS AND DISCUSSIONS

6.1 INTRODUCTION

The AES encoding and secret writing rule and therefore the implementation were mentioned within the previous chapters. currently this chapter deals with the simulation and synthesis results of the enforced AES rule. Here Modelsim tool is employed so as to simulate the look and checks the practicality of the look. Once the purposeful verification is completed, the look are taken to the Xilinx tool for Synthesis method and therefore the netlist generation.

The Appropriate check cases are known so as to check this sculptural AES encoding and secret writing rule. supported the known values because the reference the plain text and therefore the key of 128 bits are given because the input to the look and therefore the obtained cipher text ought to match the reference result. This proves that the sculptural style works properly as per the rule.

6.2 SIMULATION RESULTS

The check bench is developed so as to check the sculptural style. This developed check bench canmechanically force the inputs, that were taken from the reference, and can build the operations of rule to perform. The simulated waveforms for the varied cases are mentioned during this section.

ENCRYPTION RESULT

 

 

 

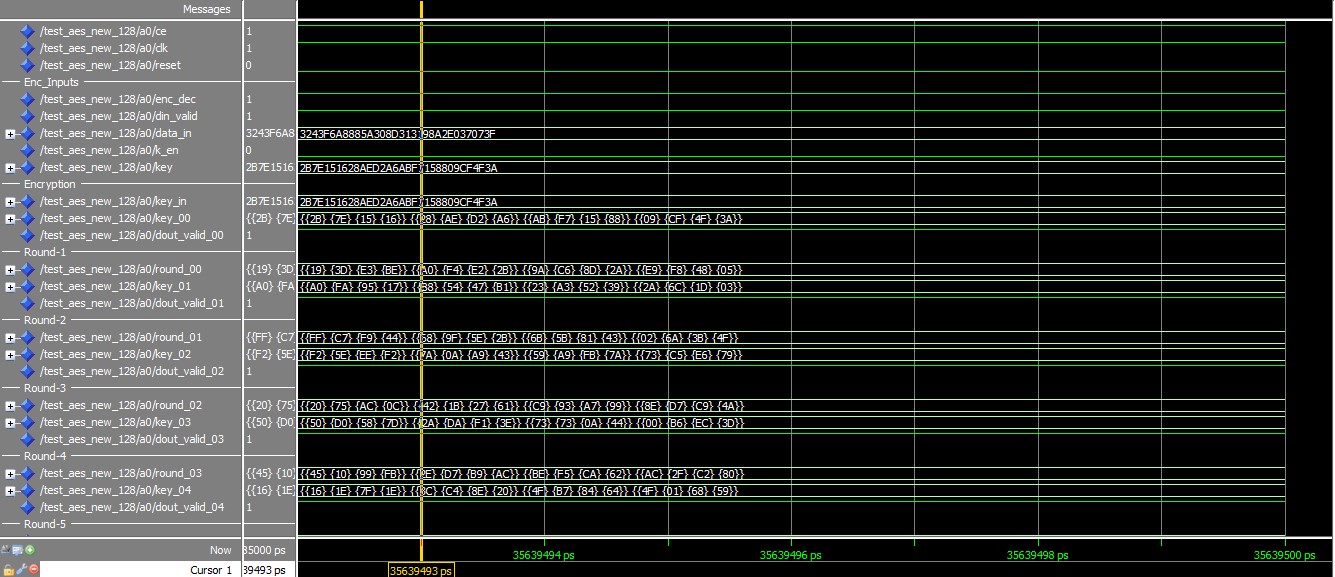
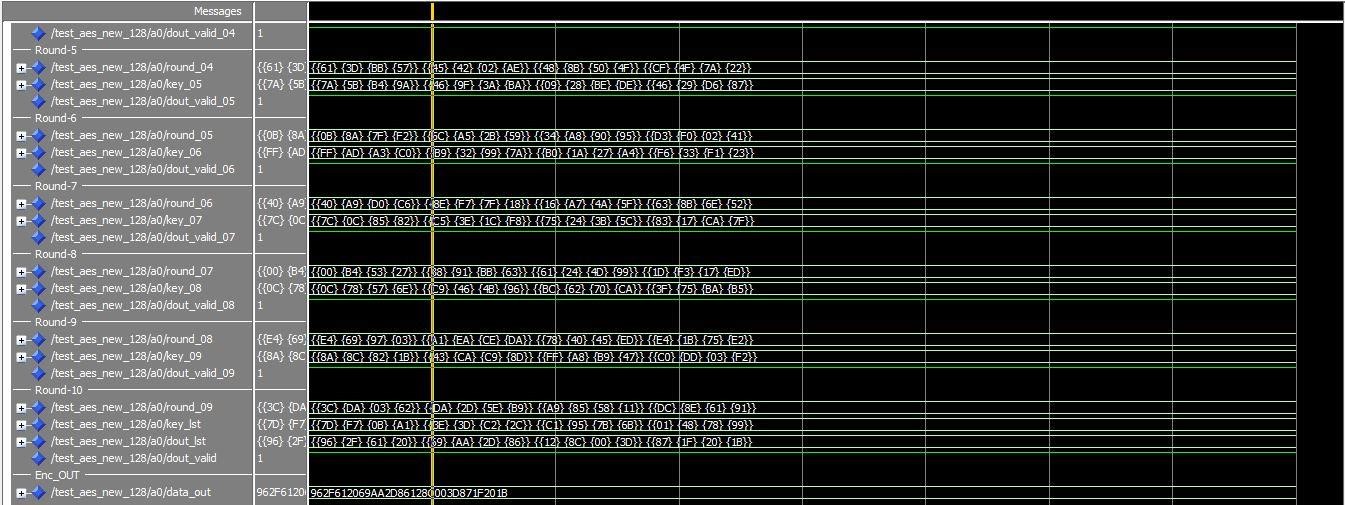
Figure 8.1 Encryption result DECRYPTION RESULT

 

 

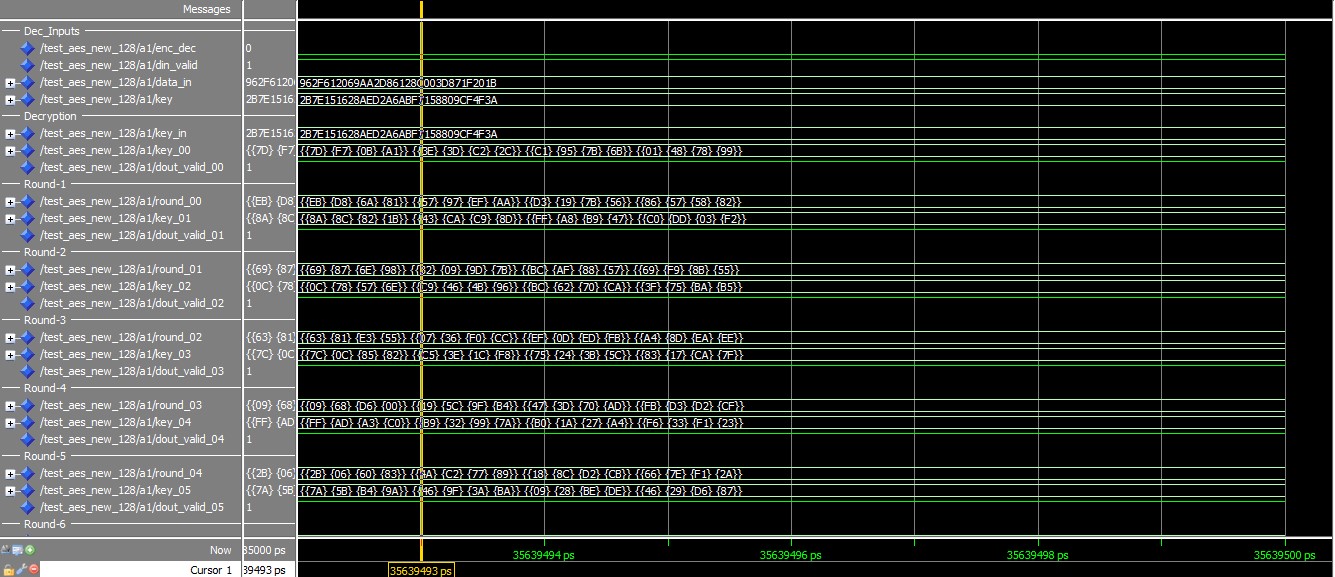
Figure 8.2 Decryption result

CHAPTER 7

ADVANTAGES, DISADVANTAGES AND APPLICATIONS

The Advantages of this algorithmic program are:
• AES is safer (it is a smaller amount vulnerable to scientific discipline than 3DES).
• AES supports larger key sizes than DES.
• AES is quicker in each hardware and software system.
• AES’s 128-bit block size makes it less receptive attacks.
• AES is needed by the newest U.S. and international standards.
• AES encompasses a parallel block cipher.

The Disadvantages of this algorithmic program are:
• AES wants a lot of process.
• It needs a lot of rounds of communication compared to DES.
• It is feasible to brute-force in finite time on fashionable processors, thus no-one uses it for all the world serious any longer.
• Sharing the key.

The Applications are:
• Many banking systems use AES-128 and AES-256 to secure on-line banking    or web banking.
• Wireless communication, like web.
• Point-of-sale terminals.
• Surveillance applications.

CHAPTER 8

CONCLUSION AND FUTURE SCOPE

10.1 CONCLUSION

Firstly, understanding the conception of cryptography and flow of AES algorithmic program is finished. winning implementation of AES algorithmic program, build to grasp one in all the secret writing ANd deciphermentcustomary accessible in market and it helps to explore the trail to implement such an algorithmic program exploitation VHDL. Mainly, the conception of representation and arrays plays a serious half in implementation. this is often a 128-bit Key dependent algorithmic program that has management over the 128-bit computer file or plaintext. the initial message is taken to ten spherical operations that produces the cipher text. This resultant encrypted knowledge is fed because the input to the decipherment and ten rounds operations were meted out and therefore a similar plain text is achieved. Given a similar input key and knowledge (plaintext or ciphertext) any implementation that produces a similar output (cipher text or plaintext) because the algorithmic program laid out in this customary is a suitable implementation of the AES.

The simulation results are verified for the various acceptable check cases. Finally the developed model is taken to the Xilinx tool and done the implementation exploitation the FPGA family of Virtex-2 board.

10.2 FUTURE SCOPE

In recent days, AES (Advanced secret writing Standard) is employed that has inflated level of security. This work on the AES secret writing and decipherment algorithmic program of 128 bits are often extended within the future within the following ways in which.
• As this algorithmic program supports the key length of 192 bits and 256 bits, the work are often extended by increasing the key length that will increase each the protection level to high and conjointly the difficulties in hacking level.
• Also this work are often extended by developing a switch. This switch are wont to switch the system of key lengths to either of 128 bits,
192 bits and 256 bits. this can be handling all the 3 key lengths and also the needed method are often meted out by with relation to the switch.

REFERENCES

[1] A. Barenco, H. H. Bennett, R. Cleve, D. P. DiVinchenzo, N. Margolus, P. Shor, T. Sleator, J. A. Smolin, and H. Weinfurter. Elementary gates for quantum computation. Physical Review A (Atomic, Molecular, and Optical Physics), 52(5):3457–3467, 1995.
[2] C. H. Bennett. Logical changeability of computation. Journal of IBM analysis and Development, 17:525–532, 1961.
[3] R. Drechsler, A. Finder, and R. Wille.Improving ESOP-based synthesis of reversible logic exploitation biological process algorithms. In Proceedings of Intl. Conference on Applications of biological process Computation (Part II), pages 151–161, 2011.
[4] K. Fazel, M. A. Thornton, and J. Rice.ESOP-based Toffoli gate cascade generation.In Proceedings of IEEE Pacific Rim Conference on Communications, Computers and Signal process, pages 206–209, 2007.
[5] D. Grosse, R. Wille, G. W. Dueck, and R. Drechsler. precise multiple controlToffoli network synthesis with Saturday techniques. IEEE Trans. on CAD of Integrated Circuits and Systems, 28(5):703–715, May 2009.
[6] W. N. N. Hung, X. Song, G. Yang, J. Yang, and M. Perkowski. best synthesis of multiple output mathematician functions employing a set of quantum gates by symbolic reachability analysis.
IEEETrans. on CAD of Integrated Circuits and Systems, 25(9):1652–1663, Sep 2006.
[7] P. Kocher, J. Jaffe, and B. Jun. Differential power analysis.
[8] Proceedings of Advances in cryptography (CRYPTO ’99), LNCS Vol. 1666, pages 388–397, 1999.
[9] R. Landauer. unchangingness and warmth generation in computing method.
[10] Journal of IBM analysis and Development, 5:183–191, 1961.
[11] D. M. Miller, D. Maslov, and G. W. Dueck. a change primarily based algorithmic program for reversible logic synthesis. In Proceedings of style Automation Conference, pages 318–323, 2003.
[12] A. Mishchenko and M. Perkowski.Fast heuristic diminution of exclusive-sums-ofproducts. In Proceedings of sixth Reed-Muller Work-shop, pages 242–250, 2001.
[13] N. Nayeem, L. Jamal, and H. Babu.Efficient reversible Montgomery multiplier factor and its applications to hardware cryptography. Journal of engineering, Jan 2009.
[14] N. Nayeem and J. E. Rice. A shared-cube approach to ESOP-based ˆ
[15] synthesis of reversible logic. FactaUniversitatis of NiE, Elec. Energ., 2011.
[16] F. Rodriguez-Henriquez, N. Saqib, A. Perez, and C. Koc.Cryptographic Algorithms on Reconfigurable Hardware. Springer: Series on Signals and Communication Technology, New York, 2006.
[17] H. Thapliyal and M. Zwolinski. Reversible logic to science hardware: a brand new paradigm. In Proceedings of forty ninth geographical area conference on Circuits and Systems (MWSCAS ’06), pages 342–346, 2006.
[18] R. Wille and R. Drechsler.BDD-based synthesis of reversible logic for giant functions. In
Proceedings of style Automation Conference, pages 270–275, 2009

APPENDIX-1

STANDARD TABLES FOR AES algorithmic rule

 

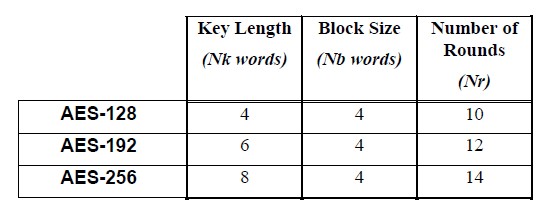
Key-Block-Round mixtures

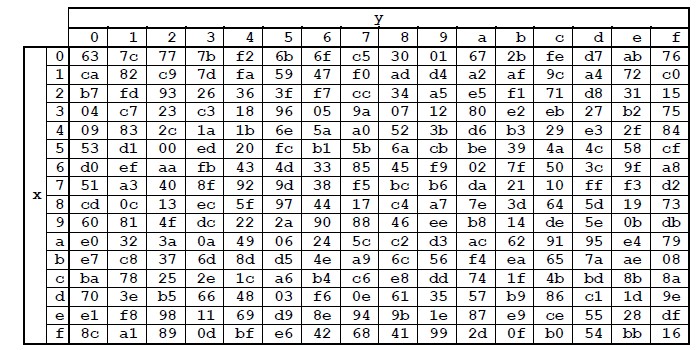
S-Box: Substitution Values employed in cryptography method


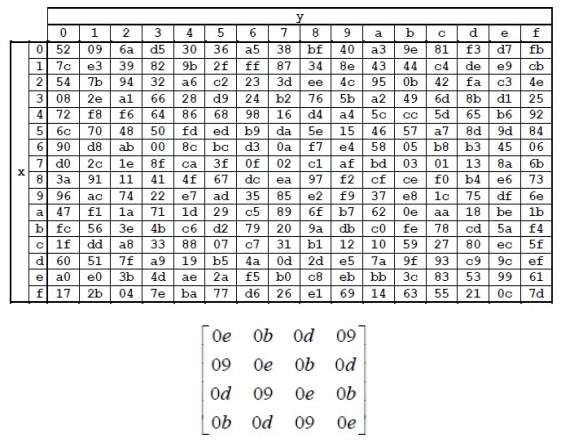
Matrix Value used in Mix Column Operation in Decryption Process