Wettability is the ability of a liquid to wet a solid surface and it is the result of intermolecular interactions between liquid and solid molecules. The degree of wetting (wettability) depends on the balance between adhesive and cohesive forces. In wetting, three phases of materials exist: gas (vapour), solid and liquid. When liquid droplets encounter solid surfaces, the physics law that applies is that the liquid tends to minimize the energy and to reach a thermodynamic equilibrium between the forces of the three phases that apply at the contact line: interactions of liquid-solid, vapour-solid and liquid- vapour.

The wettability phenomenon is found in nature’s design and is investigated thoroughly for biological [1,2], manufacturing [3], Figure 1.1, microfluidic and thermal management applications [4]. A few examples, amongst many others, of wettability phenomena in nature is the self-cleaning ability of lotus-leaves [5], Figure 1.2, and the ability of insects walking on water [6]. Understanding these phenomena, can lead to the development of fluidic-based systems for various engineering and medical applications, such as the design of superhydrophobic surfaces that can be used as antifouling coating for steel material (pipes, tankers and equipment in demanding environments), as self-cleaning surfaces that can be used in car windshields, as stain-repellers coating for textiles and as anti-soiling coatings for the construction of buildings [7]. Moreover, wettability on microdecorated surfaces is investigated also for medical applications, such as DNA mapping [8], sensors on chips [9] and the development of novel blood-diagnostic techniques [10,11], Figure 1.3.

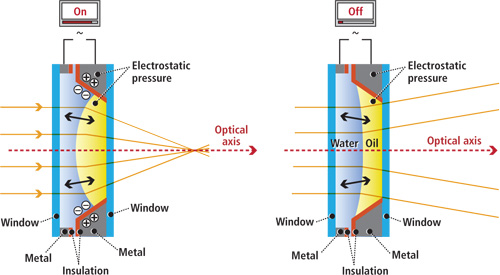
Image result for drop for tunable lenses

Figure 1.1: Wettability in tuneable lenses technology.

Droplet evaporation may be addressed as a simple issue initially; however, it is a quite complex phenomenon, that has attracted the research interest for the last century. In 1805, Young was the first who related the equilibrium of the different phases with the contact angle observation [12], and this pioneering work became the foundation of the field. Further investigation by P.G. de Gennes (discoverer of liquid crystals) on the motion of the liquid contact line [13,14] initiated further research with potential applications in the fields of lithography [15], microfluidics [16] and polymer film formation [17], amongst many others. On the microscale, the earliest investigation of micrometre-sized droplets was reported by Gudris and Kulikowa in 1924 [18]. Almost four decades later in 1962, Mangel and Baer [19] were the first to study the evaporation of sessile droplets on solid surfaces. The effect of various parameters on these volatile sessile droplets has been extensively explored, including ambient conditions, substrate properties and roughness, Figure 1.4. The evolution of droplet profile and dynamics of the contact line are dependent on these parameters. Apart from this, the nature and characteristics of the flow structure inside the evaporating droplets can be influenced by these parameters.

Related image

Figure 1.2: (a) Crop dusting and, (b) wetting on plants

Another topic that has attracted great interest amongst researchers, over the last two decades, is the evaporation of sessile droplets containing insoluble particles. The pioneering works of Deegan and co-workers [20–22], Figure 1.3, showed that particles can be moved towards the pinned contact line due to a convective outward flow and thus deposited at the droplet edge, forming a ring-like deposition pattern. This phenomenon is known as the “coffee-ring” effect. Following these pioneering publications, the evaporation of colloidal sessile droplets with the aim to control the morphology of deposition patterns left behind evaporation has been the subject of numerous studies for many scientific and industrial applications [23,24]. The studies on the drying of colloidal suspension droplets have revealed that there are different mechanisms behind the final particles distribution including the dynamics of the inner flow, evaporation kinetics, dynamics of the contact line, evolution of the droplet profile, interparticle and interfacial interactions. These mechanisms that may lead to the formation of particular deposition patterns, can be modified and controlled by manipulating a series of factors such as solute (i.e. size, concentration) [25,26], base fluid composition (i.e., surfactant) [27-30], environmental conditions (i.e., temperature, pressure) [31,32], etc. Therefore, understanding the effects of the aforementioned factors is of paramount importance for both the control and reproducibility of the deposition patterns [23,24].

Image result for drops evaporation and deposition

(a)

Image result for nanoparticles coffee stain patterns

(b)

Figure 1.3: Deposition patterns from drying drops, (a) Biomedical applications, (b) Nanotechnology and nanoparticles.

In addition to the above-mentioned findings, another topic of interest is the evaporation of sessile droplets of complex fluids such as nanofluids, Figure 1.3, polymer suspensions, and biological fluids, Figure 1.4. Although the importance of the evaporation of biological fluids and polymer suspensions is high, in this project the research focuses on the evaporation of nanofluids. Nanofluids are the dispersion of metallic or non-metallic particles with at least one dimension in the nanoscale (< 100 nm) into a base fluid [33]. Since 1995, the studies on the evaporation of nanofluids has been rapidly increasing in number due to their wide applications in electronics cooling [34], boiling [35], solar energy [36], medicine [37], and automotive industry [38]. Despite the abundant number of studies devoted to applicability of nanofluids, the full understanding of mechanisms underpinning the drying of nanofluid droplets and their pattern formation still remains elusive.

It is well understood that the rapid increasing number of studies on the particulate deposition from droplets is due to the fast-growing demand for its applications in fields such as inkjet printing [39–41], paints, nanotechnology [42], and biomedicine [43,44,45]. Despite the importance of controlling deposition patterns and numerous dedicated studies, the mechanisms behind the deposition morphology of droplets are not yet fully understood [23]. Drying of even pure sessile droplets is a complex and difficult to control phenomenon, thus much research is needed on the drying of droplets of complex fluids, Figure 1.4.

Image result for shape sessile drops

Figure 1.4: 3D modelling of evaporating drops.

This dissertation is divided in 6 Chapters: Chapters 1 and 2 include the theoretical background and the applications of the wetting phenomena of pure fluids and nanofluids on surfaces, providing the reader the information to comprehend the basis of this research work. In Chapter 3 the experimental apparatus is described along with the specifications of every component, as well as the preparation of the fluids and the manufacturing process of the microdecorated surfaces. Moreover, the software analysis and sensitivity analysis of the experimental results are described.

In Chapter 4, the experimental results on the wetting phenomena of pure fluids (ethanol) are presented and analysed, in order to provide insight into the effect of the pillar geometry on the evaporation mode and the deviation from the spherical droplet to other shapes. In detail, the shape evolution of the droplet with changing pillar-to pillar spacing and pillar geometry is analysed and discussed. Microscope investigation of the wetting phenomena unveil the pinning and depinning mode of the droplet and the thin liquid film, that is observed in certain geometries. High-speed camera investigation led to the observation of square, hexagonal and octagonal droplets, with the simultaneous thin liquid film spreading in the same shape of the droplet. Also, the thin film area was analysed, in order to provide insight into the effect of the pillar geometry on the enhancement of the imbibition phenomenon. For every different pillar geometry, different droplet volumes were investigated, in order to define the volume effect on the evaporation mode and the shape distortion of the droplet.

In Chapter 5, the experimental results on the wetting phenomena of nanofluids are presented and analysed, in order to provide insight into the concentration effect on the evaporation mode, the imbibition phenomenon and the deposition patterns of the nanoparticles. Various and diverse droplet shapes were also observed, as in Chapter 4, and the drying pattern was observed and analysed. Depending on the pillar geometry, drying patterns are categorized and further investigated with different droplet volumes, in order to determine the qualitative effect of the nanoparticle concentration on the evaporation mode and nanoparticle self-assembly. The coffee-ring effect was observed in many pillar geometries, which was also observed by other research groups on smooth surfaces. A comparison is presented, in order to define the critical pillar-to-pillar spacing, that effect greatly the droplet shape and where the coffee-ring formates.

In Chapter 7, the findings of this experimental work are discussed in comparison to the theoretical background and further investigation is proposed, as well as the conclusions of this experimental work are presented.

Chapter 2: Literature Review

2.1 Sessile droplet evaporation

A sessile droplet is a liquid droplet which is placed on a solid substrate where its contact line limits the wetted contact area between the liquid and the solid surface and characterized by droplet height (

), radius (

), and contact angle (

). The droplet evaporates if the atmosphere around the droplet’s interface is not saturated with the vapour of the solvent. Evaporation of sessile droplets is an important topic of interest for many applications such as micro-electronic cooling [46], medical diagnostic techniques [43], nanotechnology [42], painting, and printing [39-41], etc. Thus, it has attracted the attention of researchers and has led to a rapid increase in the number of publications since the 1980s.

2.2 Evaporation modes

Evaporation of sessile droplets tend to show four modes and all are depicted in Figure 1. These four evaporation modes are [47]:

The constant contact radius (CCR) mode, where the contact line is pinned and the contact radius and the wetted contact area between the droplet and substrate remain constant, whereas the contact angle decreases with time (Figure 2.1 a). There is a linear evolution of volume loss with time, revealing a constant evaporation rate for the CCR mode [48–50]. This mode is often seen with sessile droplets on rough substrates.
The constant contact angle (CCA) mode, where the wetted contact area shrinks and the contact angle remains unchanged leading to a non-linear decrease of volume with time (Figure 2.1b) [51,52]. Typically, on smooth substrates, droplet evaporation is in the CCA mode.
The mixed mode, where the evaporation mode gradually changes into another mode (Figure 2.1c) and sometimes both the radius and contact angle decrease simultaneously [52,53]. One of the most reported behaviours is the transition from CCR to CCA (Figure 2.1c) [52].
The “stick-slip” mode, where the droplet is in the CCR mode (corresponding to a “stick” phase), but the contact line suddenly slips/depins into a new position leading to a smaller contact radius when the contact angle reaches a threshold, minimum value (corresponding to a “slip” phase). Then, the droplet is again in the CCR mode (“stick” phase) until the next depinning occurs. This pinning/stick and depinning/slip of the contact line may occur for several times until the complete evaporation (Figure 2.1d). The “stick” phase lasts for longer time and accounts for the majority of the droplet lifetime, but the “slip” phase occurs rapidly. In 1995, Shanahan introduced a simple theory for the “stick-slip” evaporation mode [54]. According to Shanahan [54] and co-workers [39,55,56], when a sessile droplet is in a thermodynamic equilibrium, the free surface/interfacial energies of the system is at its minimum level. The decrease in the contact angle of the pinned droplet leads to the increase of this free energy above an energy barrier [31,55]. The pinning effect is also attributed to a potential energy barrier. When the excess free energy attains the energy barrier at a critical contact angle, the system has sufficient energy to overcome the energy barrier. Hence the contact line slips to a new equilibrium position to dissipate the excess free energy [31,55]. The droplet evaporation may proceed with the successive repetition of this cycle of the “stick” and “slip” phases.

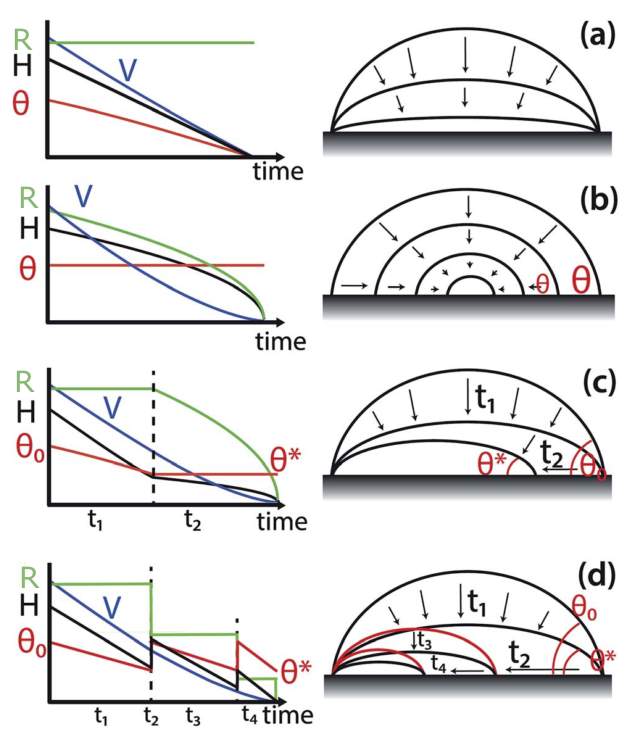
Figure 2.1. Schematic of the four possible evaporation modes of a sessile droplet: (a) Constant contact radius mode (CCR). (b) Constant contact angle mode (CCA). (c) Mixed mode (d) Stick-slip mode. The graphs show the evolution of the droplet profile (volume (V), height (H), contact radius (R), and contact angle θ) with time. Image modified from Ref. [47].

2.3 Flow fields within a drying droplet

The study of the effects of different flow fields within an evaporating sessile droplet is an important area in this research field. The capillary flow and Marangoni flow are two important flows which are commonly observed inside drying sessile droplets. Once the contact line of a droplet is pinned on the solid surface, the fluid flows radially from the central region of the droplet towards the droplet edge due to the enhanced evaporation rate at the contact line. This radially outward flow replenishes the evaporated liquid at the edge, known as the capillary flow (Figure 2.2a) [20,57,58]. Within this particular flow field, the evaporating droplet usually follows CCR where the radius is constant and the contact angle decreases [23,24,59].

Marangoni flow is driven by the surface tension gradient along the free surface of the droplet [60]. This surface tension gradient is induced by the non-monotonous distribution of local temperature [60,61] and/or concentration along the liquid-vapour interface [27,57,60]. Usually, the flow is called the thermocapillary flow (or thermal Marangoni) in the case of the temperature gradient, and solutal Marangoni in the case of concentration gradient. In an evaporating droplet, the liquid tends to flow from lower surface tension regions towards higher surface tension regions, creating Marangoni convection (Figure 2.2b). Therefore, the direction of the Marangoni flow can change depending on how the surface tension is distributed along the interface. Kim et al. [62] showed that the direction of the Marangoni flow can be changed within a water droplet containing polymers by controlling the substrate temperature. In the case of heated substrates, the temperature at the edge is higher than that at the apex, and the evaporation is enhanced at the edge, leading to the non-uniformity of the evaporation rate along the interface. As the surface tension of water decreases with increasing temperature, the liquid flows from the edge towards the top of the droplet along the interface (Figure 2.3a) [62]. Conversely, cooling substrates generate the Marangoni flow in the opposite direction to that of heated substrates (Figure 2.3b) [62].

The cooccurrence of the capillary and Marangoni flows inside the droplets is possible when the solvent evaporation causes a thermodynamic and/or hydrodynamic instability [32,63]. Kim et al. [62] found that the capillary flow is stronger than the Marangoni flow when the substrate is heated. In contrast, the Marangoni flow is more significant than the capillary flow in the case of cooled substrates.

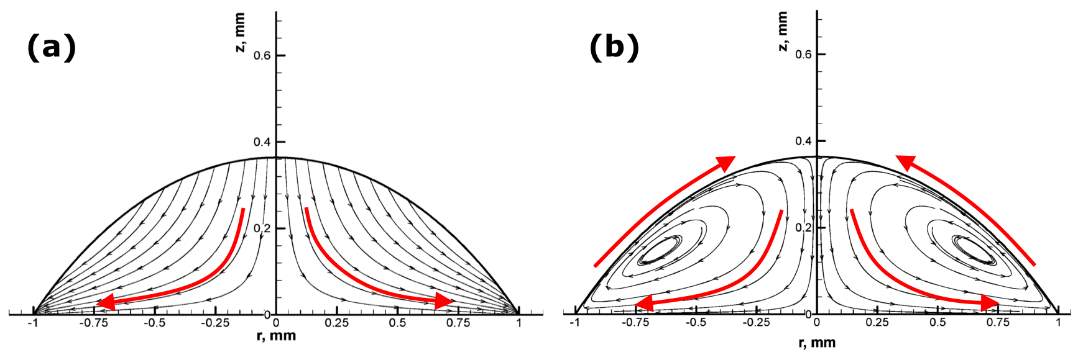
Figure 2.2. Streamline plots of the Flow field within a drying water droplet: (a) Capillary flow without Marangoni flow; Image modified from Ref. [57]. (b) With Marangoni flow; The arrows indicate the direction of the flows. Image modified from Ref. [59].

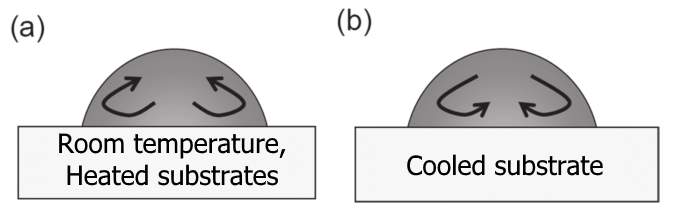
Figure 2.3. Schematic representation of the direction of the Marangoni flow inside drying water droplets: (a) Drying droplet at room temperature and heated substrate. (b) Drying droplet on cooled substrate. Image modified from Ref. [61].

2.4 Dried patterns formed by particles on the substrate

Drying liquid which contain non-volatile solutes is ubiquitous in daily life and nature such as stains after the drying of spilled tea/coffee drops on solid surfaces or rings of dust particles from dried rain drops on windows. The drying of sessile droplets with suspended particles forms various deposit patterns on solid surfaces. These interesting and complex patterns have significant influence in many applications such as biology [43,63], complex assembly [41], printing [39,64], nanotechnology [42], etc. Numerous studies have been published over the past decades to improve the understanding and controlling the deposition morphologies [23,24,59]. Macroscopic effects such as internal flow structure [21,65–67] and dynamics of the contact line [54,64,68,69], microscopic effects such as particle-interface/particle-particle interaction [70–72] significantly affect the morphologies of the final deposits. The most known of deposit patterns are described in the following subsections, patterns that have been investigated also in this project.

2.4.1 Coffee-ring pattern

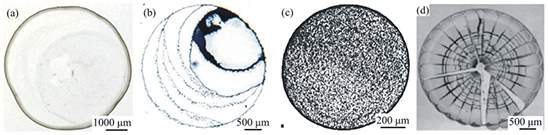
When a droplet of coffee completely evaporates on a solid surface, it leaves behind a ring-like deposit of coffee, known as the coffee-ring pattern (Figure 2.4). The related flow to this pattern is called the outward capillary flow. The geometrical constraint of the droplet behind the coffee-ring effect was explained in the pioneering work of Deegan and co-workers in 1997 [20]. They also studied the growth rate of the deposited ring, flow velocity and distribution of the particles inside the droplet [21]. During the formation of this pattern, the evaporating droplet is in the CCR mode, thus the droplet keeps its shape as a spherical cap. The height of the pinned droplet is decreased and hence the flow is pushed outward by the free surface. As the droplet is in the CCR mode and the radius is constant, liquid evaporated at the contact line must be replaced by liquid from the bulk (i.e. the centre of the drop). Thus, an outward flow inside the pinned droplet carries suspended particles towards the edge, leading to deposition of the particles near the contact line (Figure 2.5a). After the complete evaporation, a ring of concentrated particles can be seen at the perimeter of the droplet, forming the coffee-ring pattern (Figure 2.5a) [20]. Uno et al. [73] studied the dried deposit of droplets on hydrophilic substrates. They found that thin layers of particle aggregates at the perimeter of the droplet were formed (Figure 2.6) and thus hindered the decrease of the wetted contact area (self-pinning). The rapid evaporation at the upper side of the layer induced the adsorption of particles to the substrate in the layer, forming the coffee-ring pattern. According to aforementioned explanations, there are two prerequisites for the formation of the coffee-ring effect: one is the droplet pinning (CCR); and the other is the higher evaporation rate at the pinned contact line than the rest of the droplet. Later, Hu and Larson [65] demonstrated that the only two conditions of the pinned contact line and continuous evaporation of liquid are not sufficient for having the coffee-ring pattern, but the suppression of a Marangoni flow is also required. The authors found that some particles deposit at the central region of the droplet due to a recirculating Marangoni flow induced by the surface tension gradient resulting from the evaporation [65]. Therefore, the Marangoni flow should be either reduced or eliminated by manipulating some parameters (i.e., substrate temperature) to create the coffee-ring pattern. Apart from the aforementioned conditions, the droplet size is also an important factor for creating the coffee-ring pattern [74]. Shen et al. [74] showed that a very rapid evaporation process inhibits a successful coffee-ring formation, as the suspended particles do not have sufficient time to reach and deposit at the edge. They experimentally demonstrated that there exists a lower limit of droplet size for having the coffee-ring pattern. For particle concentration above a critical value, the lower limit of the droplet size can be estimated by the competition between liquid evaporation and the diffusive particle motion inside the droplet. The minimum diameter of the droplet with the coffee-ring pattern was found to be approximately 10 nm for the particle size of 100 μm [75].

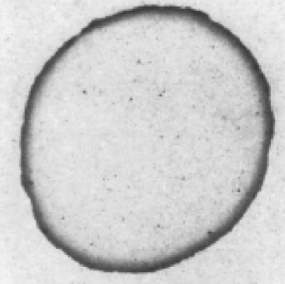
Figure 2.4. Coffee stain left after the drying of a coffee drop following the CCR mode. Image modified from Ref. [22].

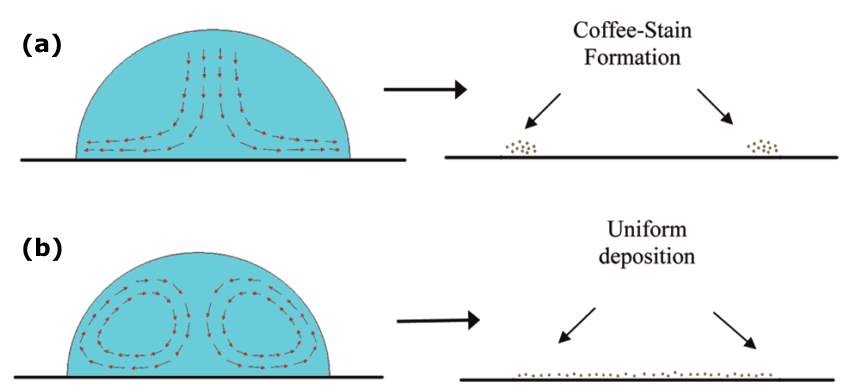Figure 2.5. Evaporation of a colloidal drop under ambient conditions: (a) Outward flow in a droplet creates a coffee-ring stain. (b) Recirculating Marangoni flow creates a uniform pattern. Image taken from Ref. [66].

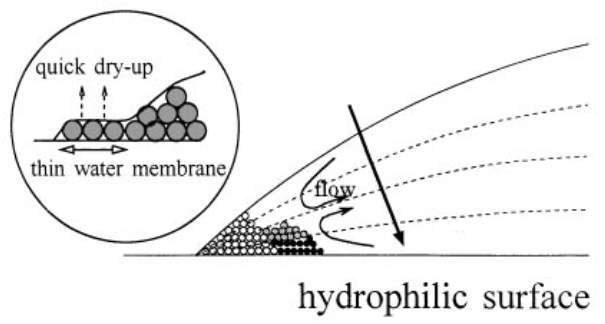
Figure 2.6. A schematic representation of particles motion and pattern formation inside a drying droplet on a hydrophilic surface with CCR mode. Insets show the magnification of the contact line. Image taken from Ref. [73].

2.4.2 Uniform pattern

Much attention has been devoted to altering the “coffee-ring” effect as uniform deposition patterns are required in many research fields such as coating [75], inkjet printing [64], and biological assays [76]. However, such uniform patterns are not easy to achieve due to the domination of the “coffee-ring” effect inside the droplet [76]. As mentioned in the previous section, the evaporation of droplets in CCR mode with the either sufficient suppressed or elimination of the Marangoni effect leads to the formation of the coffee-ring pattern. In the case of high concentration of particles, a drying droplet in CCR (with the negligible Marangoni effect) may leave a ring-like pattern, but with the uniform distribution of particles in the region enclosed by the ring [77,78] (Figure 2. 7). As an example by Thokchom et al. [67], a monolayered, uniform nanoparticle structure was left behind after the dry-out of droplets on hydrophilic substrates, in which the Marangoni effect was completely suppressed and the outward capillary flow dominated in the flow field. The concentration of nanoparticles was slightly higher than the theoretical concentration for filling the wetted contact area, inhibiting the coffee-ring effect.

The alteration of the internal flow may also form uniform patterns. Majumder et al. [66] showed that the recirculating Marangoni flow within a droplet on a hydrophilic substrate prevents particles from accumulating at the pinned edge and transports them towards the top of the droplet along the air-liquid interface (Figure 2.5b). The Marangoni flow keeps the particle concentration homogenized, inhibits coffee-ring pattern and forming a uniform pattern (Figure 2.5b).

Uniform patterns can be also formed by controlling the evaporation kinetics and/or interactions inside the droplet (i.e., particle-particle, particle-substrate, and particle-liquid interactions) [71,72,79]. Bigioni et al. [76] reported a highly uniform, long-range-ordered compact monolayer of nanocrystals created by enhancing the evaporation rate and also attractive particles interaction with the free interface of the droplet. Similarly, Li et al. [72] demonstrated that the sufficient enhancement of evaporation rate leads to the accumulation of particles at the air-liquid interface rather than at the edge, surpassing the coffee-ring effect. Those particles located at the interface deposit in the interior, and hence form a uniform deposition of particles in the interior with a thicker ring at the edge. In the work by Bhardwaj et al. [70], the solution pH was varied to modify the particle-particle and particle-substrate interactions, which led to the alteration of the final deposit patterns. At low pH value, particles in the vicinity of the substrate were attracted to the substrate and formed a ring-like pattern with a uniform deposition of particles in the interior of the ring due to the attractive particle-substrate interaction. At intermediate pH value, the aggregation of particles was formed as the particle-substrate interaction was weaker than the particle-particle interaction. Aggregates randomly covered the entire initial wetted contact area. However, at high pH value, the ring-like pattern was formed with almost no particle in the interior of the ring due to the strong repulsive particle-substrate interaction.

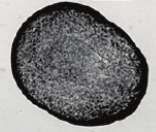
Figure 2.7. Uniform pattern with an outer thick ring. Image taken from Ref. [70].

2.4.3 Stick-slip pattern

If a colloidal droplet evaporates following the stick-slip mode, a set of concentric rings are left on the substrate after the complete evaporation [69], as shown in Figure 2.8a. During the “stick” phase of the “stick-slip” mode, particles accumulate at the contact line and form a ring. Then, the contact line slips to a new position, and particles again form another ring. Consequently, the cycle of the “stick” and “slip” phases leads to the formation of a multiple concentric rings of particles on the substrate. The contact line usually sticks and slips on one side of the droplet, while it remains pinned on another side for all evaporation time, presumably due to the irregularities on the solid surface [77]. Unexpectedly, the study of the droplet profile showed that the sticking of the contact line is not complete during the “stick” phase; there is a slight drift of the contact line, known as the “pseudo-pinning” (see variation of the droplet radius over time in Figure 2.8b) [69,77,81].

Two explanations are proposed for the “pseudo-pinning” of the contact line: one is the small-scale pinning of the contact line by the deposited particles; and the other is the increased local viscosity at the contact line by the higher concentration of particles [69,81]. Adachi et al. [82] formulated a mathematical model to explain the mechanism behind the oscillatory motion of the contact line during the stick-slip mode, which leaves a striped pattern after the complete drying. The contact line bore a friction force when the particles move from the centre to the edge. The competition between the friction force and surface tensions at the contact line results in the oscillatory motion of the contact line, forming the striped stain pattern. Hence, the pinning or depinning of the contact line is not important because the competition between the forces determines the behaviour of the contact line [24,82].

Figure 2.8. (a) “Stick-slip” pattern. Each ring of particles corresponds to the “stick” phase in the “stick-slip” mode. (b) Contact radius and contact angle versus evaporation time. Image modified from Ref. [69].

2.4.4 Combined pattern

In some cases, a combined pattern of two or more pattern types appears on a substrate. As an example, Crivoi and Duan [83] reported the formation of the fingering pattern in the interior of the coffee-ring after the complete evaporation of a water-based copper nanofluid droplet (Figure 2.9 a). It was found that the nucleation and growth process inside the peripheral ring results in the formation of this combined pattern. A combined pattern of ring-like and dot-like patterns was observed after the full evaporation of a drop containing a mixture of surface-inactive and surface-active solutes on a substrate with weak contact angle hysteresis, as shown in Figure 2.9b [84]. By analysing the drop shape evolution during the last stage of the evaporation, it was found that the contact line was pinned due to surfactant adsorption and this led to the ring-like pattern formation. Then, the depinning of the contact line started from a corner, and most parts of the contact line receded towards the part that was unpinned. Finally, the precipitation of surface-inactive solutes occurred close to the pinned part of the contact line, and led to the dot-like pattern formation inside the peripheral ring. Nguyen et al. [85] observed inner coffee-ring deposits (ICRDs) inside the initially pinned contact area of the dried water-based SiO₂ nanofluid droplets on smooth hydrophobic substrates (Figure 2.9c). In addition, dendrite-shaped patterns were observed inside ICRDs. The formation of the combined patterns was explained by the late secondary pinning of the contact lines which occurred after the initial pinning. The balance of the forces on nanoparticles led to the secondary pinning. The size and patterns of ICRDs were found highly dependent on nanoparticle concentration, contact angle hysteresis, and nanoparticle interaction forces. Drying biofluid drops often form complex patterns which are the combination of different deposition patterns. Figure 2.9d shows the dried pattern of blood serum from a healthy person which is the combination of two crack and crystal patterns [86]. As shown in Figure 2.9d, the deposit is characterized by two parts: one is the peripheral part which is composed of radial and orthoradial cracks (Figure 28dI); the other is the central part which is composed of different morphologies of crystal pattern such as dendrites and inclusions (Figures 2.9dII,III).

Figure 2.9. Combined patterns: (a) Fingering pattern inside the coffee-ring pattern. Image modified from Ref. [88]. (b) Dot-like pattern inside the coffee-ring pattern. Image modified from Ref. [89]. (c) Dendrite-shaped pattern inside the inner coffee-ring deposit. Image modified from Ref. [90]. (d) Crystal pattern enclosed with the crack pattern: (I) Radial and orthoradial cracks in the peripheral part of the deposit, (II) Dendrites in the central part of the deposit, and (III) Inclusions in the central part of the deposit. Image modified from Ref. [86]

2.5 Effects of different factors on deposit patterns

In the previous section, a series of dried patterns are discussed which are significantly affected by evaporation kinetics, the movement of contact line, inner flow structure, interfacial interactions, and particle-particle interaction. the mentioned effects are dependent on the factors which can be manipulated to control the pattern formation of drying drops. These factors that affect dried patterns are discussed in the next subsections.

2.5.1 Concentration

Particle concentration has a significant influence on the final deposition patterns. Sefiane [44] investigated the effect of concentration (0.1, 0.5, 1 and 2%) on the final deposition patterns of Al₂O₃ nanofluid drops. Ring-like patterns were observed for all concentrations and the thickness of the ring increased with increasing concentration. Cellular cracking patterns were also found which were more prominent at higher concentrations. Increasing concentration increased the thickness of these cells. Brutin [26] observed a transition between two patterns that corresponded to a critical concentration, as seen in Figure 2.10. For concentrations between 0.01 and 0.47 wt %, a coffee-ring pattern with no particles in the interior of the ring was formed. The width of the ring decreased with increasing concentration following a power law. For concentrations above 1.15 wt %, nanoparticles deposited in the central regions, forming a “flower petal” pattern. The deposition thickness increased with increasing concentration, whereas the number of “flower petals” decreased with concentration.. At moderate concentrations and particle sizes, an irregular pattern was formed.

Figure 2.10. Influence of nanoparticle concentration on final deposition patterns. Coffee-ring pattern is formed for concentration between 0.11 and 0.47 wt %, and a flower petal pattern is formed for concentration between 1.15 and 5.7 wt %. Image taken from Ref. [26].

Moffat et al. [81] showed that drying nanofluid droplets with concentration of 0.01 wt % had a receding contact line with distinct decrease in contact angle. However, drying nanofluid droplets with concentration of 0.1 wt % showed the “stick-slip” behaviour. The increase of nanoparticle concentration enhances the “stick-slip” behaviour [54,81]. A direct correlation was found between the distance jump by the contact line and nanoparticle concentration [54]. The higher concentration leads to a longer pinning of the contact line, thus the deviation in contact radius from equilibrium before a jump is higher and the steps of the contact line are greater [55].

2.5.2 Material

Lee et al. [87] made a comparison between the deposition patterns of the 20 nm Al₂O₃ and 21 nm TiO₂ nanofluid drops at the same concentration of 0.05 vol % (Figure 2.11). The ring width of the Al₂O₃ nanoparticles was found to be smaller than that of TiO₂ nanoparticles. By considering the effect of different factors such as the material, size, and concentration of nanoparticles, the authors concluded that the material of nanoparticles has a less significant role on the pattern formation. As seen in Figure 2.12, the pattern formed by the mixture of the 5 nm graphite and the 5 nm Al₂O₃ nanoparticles is similar to the pattern of the Al₂O₃ nanoparticles [88]. However, the gap between the contact line and the centre-concentrated deposit is larger for the mixture pattern than that for the Al₂O₃pattern. The effect of the combination of the two nanoparticles is found to be collaborative on the mixture pattern as they almost keep their position as in the patterns formed by either graphite or Al₂O₃ nanoparticles.

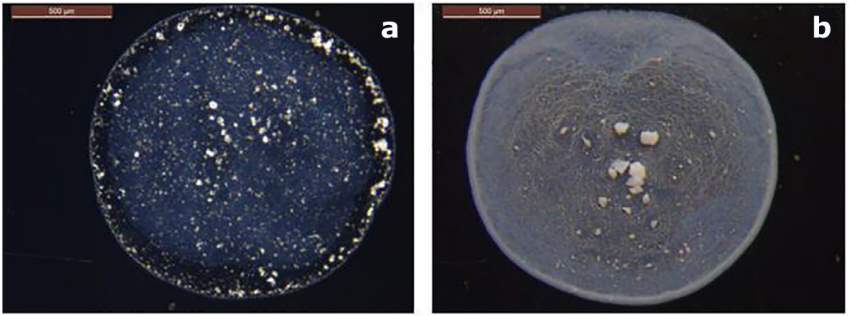
Figure 2.11. Deposition patterns after drying sessile drops containing different materials of nanoparticles: (a) 20 nm Al₂O₃and (b) 21 nm TiO₂ with 0.05 vol % concentration on stainless steel. Image taken from Ref. [88].

Figure 2.12. Deposition patterns after drying sessile drops containing single 5 nm graphite nanoparticles, the single 5 nm Al₂O₃ nanoparticles, and the mixture of graphite and Al₂O₃ nanoparticles. Image taken from Ref. [88].

2.5.3 Environmental conditions- Ambient temperature and pressure

An investigation was carried out to find the effect of the environmental temperature on the deposition patterns of the dried TiO₂ and Al₂O₃ nanofluid drops [44]. At the same concentration, the deposition pattern of Al₂O₃ nanoparticles was relatively independent of the ambient temperature. However, in the case of TiO₂ nanofluid, increasing the temperature led to the ring-like pattern formation with the concentric rings in the interior of the peripheral ring.

Askounis et al. [31] investigated the influence of reduced atmospheric pressure varying from 750 to 100 mbar on the final deposition patterns left after the full evaporation of water drops containing SiO₂nanoparticles ( Figure 2.13). Reducing the atmospheric pressure enhanced the evaporation rate due to the increase of the effective diffusion coefficient of water vapour in the environment. The evaporating drop followed the “stick-slip” mode under 750 mbar pressure, and hence the “stick-slip” pattern was formed (Figure 2.13a). However, the ring-like pattern was formed under 500 mbar pressure (Figure 2.13b), and a wider and thicker ring was obtained with a further reduction of pressure to 250 mbar (Figure 2.13c). The outward flow contributed to the accumulation of nanoparticles at the contact line and thus enhanced the pinning effect which both led to the formation of the ring-like patterns, but the thicker ring resulted from the stronger outward flow caused by the further reduction of the pressure. At 500 mbar pressure, the assembly of hexagonal, closed-packed nanoparticle structures was also observed. A different ring-like pattern with an inner irregular shape was formed under 100 mbar pressure (Figure 2.13d). The high deposit was brought near the edge by the very strong outward flow induced by the extremely high evaporation rate. Moreover, the fast evaporation did not give sufficient time to the fluid to flow towards the edge, and thus became frozen in place, forming the different inner deposits from those drops under 250 and 500 mbar. From the nanoscopic point of view, nanoparticle pattern crystallinity was promoted with reducing pressure.

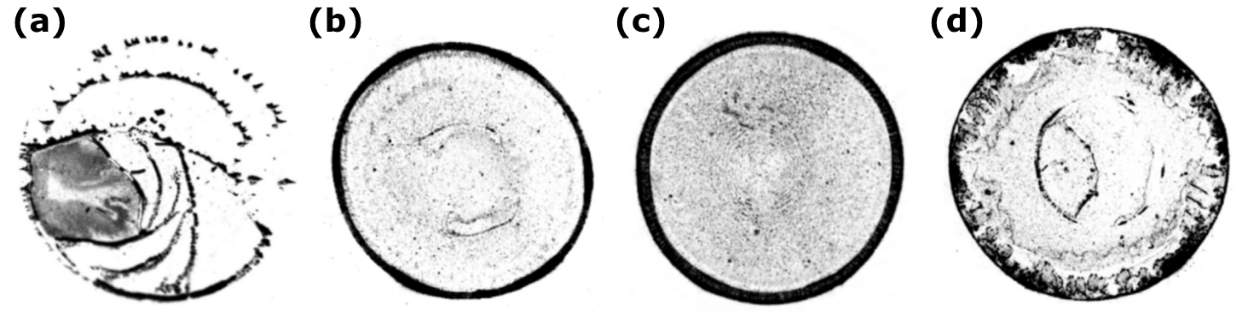
Figure 2.13. Influence of reduced environmental pressure on the pattern formation of a sessile SiO₂ nanofluid drop: (a) 750 mbar, (b) 500 mbar, (c) 250 mbar, and (d) 100 mbar. Image modified from Ref. [31].

2.5.4 Base fluid composition

It is noteworthy that pure water has been widely used as the base fluid in the studies relevant to the pattern formation from sessile drops. Change in the base fluid composition can be a way to control the particle deposition morphology of a drying colloidal droplet.

As an example, Choi et al. [89] made a comparison between the effect of Newtonian and non-Newtonian base fluids on the pattern formation of 6 μm polystyrene particles suspended in aqueous solutions of water, PEO, and xanthan gum (XG). The evaporation of XG solution formed the coffee-ring pattern, while a more inner uniform pattern with no distinct ring was formed after the evaporation of water and PEO solutions. The difference in the deposition patterns observed between the PEO and XG solutions was attributed to the difference between their viscosities. The viscosity of the XG solution remains high during low shear drying as it has a very high zero shear viscosity. For higher viscosity fluids, the capillary flow transport larger particles towards the drop edge at the early stages of the evaporation, and thus leading to the formation of the coffee ring pattern. Talbot et al. [90] studied deposition patterns from drying colloidal droplets influenced by two binary base fluids of water-ethylene glycol and water-ethanol. Uniform patterns enclosed with thick rings were formed at low concentration (10 and 30 vol %) of ethylene glycol in water, as shown in Figure 2.14. At higher concentration of ethylene glycol (50 – 90 vol %), ring-like patterns were formed with the less dense interior regions. For concentrations above 70 vol %, unfilled regions were also observed inside the peripheral rings. Ethylene glycol-water mixture droplets showed rapid particle movement toward the contact line as water evaporates first. When ethylene glycol dominated the drying process, particle movement slowed down but still remained radially outward. At high concentration of ethylene glycol (i.e., 90 vol %), no inward Marangoni flow was observed, thus a slow radial flow dominated the evaporation, leading to the formation of the rings. For low concentration of ethylene glycol (i.e., 10 vol %), there was a more rapid outward flow. The uniform coverage inside the rings was attributed to particles that did not have enough time to reach the edge after the evaporation process was dominated by ethylene glycol.

Drying water-ethanol binary-based droplets formed ring-like deposits. The width of the rings increased with increasing ethanol concentration from 10 to 90 vol %. At the beginning of evaporation for the ethanol concentrations between 10 – 50 vol %, inner flows showed particles collected at the central regions until the drying process was dominated by water. Then, the radial outward flow dominated the flow field. At ethanol concentration of 90 vol %, the flow slowed down, and lower contact angle facilitated pinning of the contact line, forming a ring-like deposit. As shown in Figure 2.15, the deposition patterns of water-ethanol binary-based nanofluid droplets are affected by the ethanol concentration [36]. The evaporation of pure water-based suspension formed a nearly uniform pattern (Figure 2.15a). However, at the ethanol concentration of 10 vol %, most nanoparticles deposited in the centre of the droplet and detached from the peripheral ring (Figure 2.15b). The dried pattern showed uniformity again as the ethanol concentration increased to 25 vol % (Figure 2.15c). However, the inner deposit started to detach from the peripheral ring with a further increase of the ethanol concentration to 40 and 50 vol % (Figure 2.15d,e).

Figure 2.14. Deposition patterns from ethylene glycol-water binary-based droplets containing 1 vol % 220 nm spheres (Scale bar 20 μm). Image taken from Ref. [85].

Figure 2.15. Influence of the ethanol concentration on the pattern formation of 1.5 g/L graphite-water nanofluid droplets: (a) 0 vol %, (b) 10 vol %, (c) 25 vol %, (d) 40 vol %, and (e) 50 vol %. Image modified from Ref. [28].

2.6 Regular Geometrical Drops

Research interest is now focusing on droplet evaporation and the deposition of nanofluids suspension on micropatterned surfaces, where there is the ability to control fluid shape, evaporation rate and particle deposition pattern. This ability is provided through designing surface structure and pillar-to-pillar spacing on the surface according to the evaporation rate of different fluids and nanofluids. Shape control of the droplet, which deviates from sphere (axisymmetric) to square, rectangular or octagons, have been investigated on different micropatterned surfaces [91, 92].

Related image

Figure 2.16: Superhydrophobicity achieved on patterned surfaces.

Surfaces with different pillar geometry and pillar-to pillar spacing have been investigated, where except from the different droplet shapes, thin liquid films were observed on the surfaces simultaneously or not with droplets. This phenomenon is called imbibition and research focuses on the effect of the microstructure on the liquid thin film direction, spreading, pinning and depinning pattern [93, 94]. Research of liquid dynamics on microdecorated surfaces, which imitate nature’s design, can provide insight and tools for fine manipulation of pure fluid wetting and nanofluid deposition pattern, with various and diverse applications in biology, manufacturing and thermal management [95].

Figure 2.17: Shape transformations observed during cooling of emulsion droplets of pure hydrocarbons in water, in the presence of 1.5 wt% surfactant. [96]

Figure 2.18: Choice of surfactant and cooling rate can determine particle shape and aspect ratio [96].

Although the evaporation of droplets and the drying patterns of nanofluids have drawn the research interest for many years, it is still a field that has not been completely comprehended and fully described. Especially, the effect of the geometry and roughness of micropatterned surfaces on the liquid shape control, the wetting mode and the nanoparticle deposition pattern, have not been extensively investigated. Therefore, it is the scope of this dissertation to present the experimental work on the wetting phenomena on microdecorated surfaces of pure fluids and nanofluids, to analyse and discuss the effect of the pillar geometry on the evaporation pattern and the nanoparticle deposition pattern.

Figure 2.19: (a) liquid droplets spreading over chemically homogeneous microtextured substrates form polygonal shapes, (b) Final shapes for droplets of different liquids released on the same surface [97].

Figure 2.20: The design of the microtexture allows for the control of the locus, size and shape of spreading droplets [97].

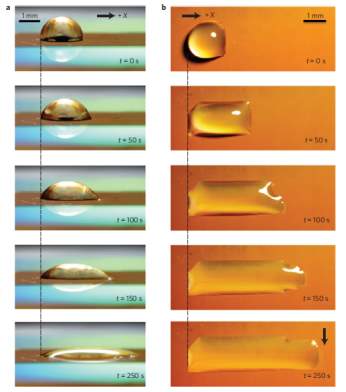
Figure 2.21: Time-lapse images of uni-directional spreading of a liquid droplet. a,b, Side view (a) and top view (b) of a 1 l droplet of deionized water with 0.002% by volume of surfactant spreading on a surface with pillar diameters of 500 nm, spacings of 3:5 m and heights of 10 m (with a height-to-spacing ratio of 2:87;H/lD2:87) deflected [98].

2.7 Conclusions

Following the above literature survey, it is obvious the depth and breadth of interest by researchers in the topic of droplets evaporation and drying. Patterns from these drying drops can take various shapes. Operating parameters such as ambient conditions as well as the nature of the substrate (thermal properties and roughness) can significantly influence the final pattern of the deposits. This has been extensively studied by groups around the world as demonstrated by the above literature review.

Moreover, geometrical shapes can be generated by drops on patterned surfaces through imbibition. This has been demonstrated for specific cases of water for pico droplets. The ability to generate square, rectangular, triangular…etc, droplets opens the door to a host of potential applications. Understanding the underlying mechanisms of the formation of these geometrical shapes remains however elusive. Further studies on this phenomenon are definitely required.

The use of nanoparticles suspensions combined with droplets evaporation is another topic widely studies as shown in the above literature review. The deposits from these nanofluids, can be influenced by operating parameters as well as surface structure. The investigation of drying of nanofluids droplets using geometrical droplets, has not been undertaken to the best of our knowledge.

Chapter 3: Experimental setup and procedures

3.1 Experimental equipment

The main experimental technique used in this study was Drop Shape Analysis. Also, the substrates used in the experiments were micropatterned polymeric substrates, with various pillar geometries, manufactured with microfabrication techniques at Scottish Microelectronics Centre (SMC).

3.1.1 Drop Shape Analysis

The experimental equipment used was a Krüss DSA30 (Krüss GmbH, Hamburgh, Germany) Drop Shape Analyser (DSA). The instrument was used to deposit droplets and record the evaporation phenomenon over time. The DSA was equipped with an automated dosage system, which gives the ability to control the volume and deposition of the droplets. This volume precision dosage system allowed the volume control across a range of droplet sizes, which in this study provided the ability to correlate the volume effect to shape evolution and the asymmetries of the droplets. The DSA is also equipped with a CCD camera and a backlight to provide contrast. These equipment components allow the recording of the droplet profile during evaporation (droplet volume, contact angle and contact radius).

In addition, a second CCD camera, placed at a 45° angle of the surface view to the first camera, allows the recording of the shape evolution of the droplet overtime. The mounted on the DSA second CCD camera recorded at the same experimental time the shape evolution of the droplet, to point out potential asymmetries from the circular shape and to provide the ability to correlate the contact angle data to the actual droplet shape. The features of the second CCD camera are presented in the table 3.1, along with the specification of the lens that was mounted on the camera.

C:Users
tekiAppDataLocalMicrosoftWindowsINetCacheContent.Word20170706_161742.jpg

Figure 3.1: Experimental equipment, consisting of the DSA30 and mounted CCD camera.

Table 3.1: Camera and lens specifications

CCD Camera	1.3 Megapixel Color CMOS Camera with USB 3.0 Interface
Resolution	1.3 MP 1280 × 1024 pixels
Sensor type	CMOS RGB Bayer Matrix
Sensor active area	6.9 × 5.5 mm
Framerate	60fps
Lens	Nikkon AF MICRO 105 mm 1:2.8 D LENS -NIKKOR
Optics	9 elements in 8 groups
Minimum focus distance	0.314m
Working distance	133 mm

The Drop Shape Analyzer was connected to a PC and all measurements and analysis were done using the dedicated software ADVANCE 1.5.

The measurements were conducted by lowering the needle tip until 5mm above the pre-cleaned substrate. With the use of the electronic control dosage system, a droplet of the desired volume was created and afterwards the needle tip was lowered to deposit gently the droplet on the surface. At this stage, the needle was withdrawn from the field of view, and the recording of the evaporation started with both cameras, the DSA’s CCD and the second camera (top view). The number of frames that were captured depended on the evaporation rate. Approximately, 300 fps were recorded for droplet volume from 1 µL to 4 µL and 600 fps were recorded for droplet volume from 5µL to 10 µL. The experimental conditions were 1 bar pressure, relative humidity was around 30% and temperature of 20°C. After the end of the experiment, the analysis with the software ADVANCE 1.5 determined the droplet contact angle, contact radius and volume, over time. The second camera measurements allowed the analysis of the shape evolution of the droplets, and the correlation to the total or local droplet profile, in two groups: symmetrical and asymmetrical and various droplet shapes respectively. The determination of the droplet profile was conducted using the tangent fitting method. Since for the specific experiments a wide range of measured contact angles θ (10° to 180°) was investigated, and it was found that the tangent fitting method is suitable for the whole.

The experimental equipment is presented in Figure 3.1 , pointing out with numbers the components and providing their description.

The experimental equipment consists of 6 main components, see Figure 3.1. The second CCD camera (1), mounted on a post at 45° angle to the substrate, in order to collect data for the evolution of the droplet shape. The NIKKON lens (2), attached to the camera, adjusted to the specific working distance and the desired field of view. The backlight of the DSA30 (3) was also adjusted in order to provide better contrast, for the contact angle measurement. The substrate (4), which is a micropatterned Si wafer. The CCD camera (5), to capture frames for the contact angle measurement, at the same level with the substrate. The automated, motorised dosage system (6), equipped with 1ml BD Plastipak syringe.

3.1.2 Scanning Electron Microscopy

Scanning electron microscopy (SEM) measurements were conducted, in order to assess the self-assembly behaviour of the nanoparticles deposition. Surface/deposits were visualised with a scanning electron microscope (SEM, Versa 3D, FEI Co., USA), operating at 15kV and 3.3 pA. Surface features were measured with a 3D laser-scanning microscope (OLS400, Olympus, Tokyo, Japan), Figure 3.2. Experiments were conducted in collaboration with Dr. Alexandros Askounis, Kuyushu University, Japan.

Figure 3.2: Focused Ion Beam Scanning Electron Microscope

3.1.3 Substrates fabrication

Fig1
The surfaces were fabricated on Si wafers using photolithography, reactive ion etching and molecular vapour deposition. SPR 220-7.0 positive photoresist was spun on to a Si wafer and exposed through a photomask. Silicon deep reactive ion etching was then carried out to etch the areas of the wafer not insulated from the process by photoresist. This allowed structures of known lateral dimensions (defined by the photoresist pattern) and height (defined by the etching process to be 10 µm) to be engraved in the surface. The surfaces formed uniform arrays of microstructures with four different lateral morphologies; square, circular, triangular or star-shaped, shown in Figure 3.3.

Figure 3.3. SEM images of (a) square, (b) circular, (c) triangular and (d) star-shaped pillars, 10 µm in height.

The arrays comprised distinct repeating spacing between structures of 5, 10, 20, 40, 80 or 160 µm. Finally, the surfaces were coated with perflourodecyltrichlorosilane (FDTS) using molecular vapour deposition. The coating has an intrinsic hydrophobicity that is enhanced by the microstructure of the surfaces. The wafer consisted of 61, same sized, square sub-surfaces. Each subsurface had different pillar shape, pillar lateral dimensions and pillar spacing. Of these 61 surfaces, 53 were studied for the evaporation of pure and nanofluids, in various volume and nanoparticle concentration. In Table 3.2, the pillar shape, dimension and spacing are presented.

Table 3.2. Surface plan

Number	Lateral Morphology	Lateral Dimensions (X × Y µm²)	Spacing (µm)
1	Square	5 × 5	5
2	Square	10 × 10	10
3	Square	5 × 5	10
4	Square	5 × 5	20
5	Square	5 × 5	40
6	Square	5 × 5	80
7	Square	10 × 10	5
8	Square	10 × 10	20
9	Square	10 × 10	40
10	Square	10 × 10	80
11	Square	10 × 10	160
12	Square	20 × 20	5
13	Square	20 × 20	10
14	Square	20 × 20	20
15	Square	20 × 20	40
16	Square	20 × 20	80
17	Square	20 × 20	160
18	Square	20 × 20	320
19	Square	40 × 40	5
20	Square	40 × 40	10
21	Square	40 × 40	20
22	Square	10 × 10	10
23	Square	40 × 40	40
24	Square	40 × 40	80
25	Square	40 × 40	160
26	Square	40 × 40	320
27	Square	10 × 10	10
28	Rectangular	20 × 10	10
29	Rectangular	40 × 10	10
30	Square	10 × 10	10
31	Square	10 × 10	10
32	Square	10 × 10	10
33	Rectangular	60 × 10	10
34	Rectangular	80 × 10	10
35	Square	10 × 10	10
36	Circular	10 × 10 × π	5
37	Circular	10 × 10 × π	20
38	Circular	10 × 10 × π	40
39	Circular	10 × 10 × π	80
40	Square	10 × 10	10
41	Circular	10 × 10 × π	160
42	Rectangular	100 × 10	10
43	Triangular	0.5 × 10 × 10	5
44	Triangular	0.5 × 10 × 10	10
45	Circular	10 × 10 × π	10
46	Triangular	0.5 × 10 × 10	20
47	Triangular	0.5 × 10 × 10	40
48	Triangular	0.5 × 10 × 10	80
49	Triangular	0.5 × 10 × 10	160
50	Star (6-point)	10 × 10 – (23.38)	5
51	Star (6-point)	10 × 10 – (23.38)	10
52	Star (6-point)	10 × 10 – (23.38)	20
53	Star (6-point)	10 × 10 – (23.38)	40
54	Star (6-point)	10 × 10 – (23.38)	80
55	Star (6-point)	10 × 10 – (23.38)	160
56	Plane	10000 × 10000	0
57	Nested Square Flat Tori	(R × R) – ((R-5) × (R-5))	5
58	Nested Flat Tori	((π × R^2) – (π × (R-5)^2)	5
59	Square	10 × 10	10 – 91 (Δ = 1) From Centre
60	Square	10 × 10	10
61	Square	10 × 10	10 – 132 (Δ = 1) L-R X-axis

In addition to the DSA30 and the SEM, an optical microscope was used to visualise larger scale. Areas adjacent to the contact line were observed using high magnification optical microscopy.

3.2 Experimental procedures

3.2.1. Pure fluids

Deionised water was used for the cleaning of the substrates and ethanol was used for the preparation of solutions for this study. Deionised water was obtained from a Barnstead NANOpure© DiamondTM Analytical ultrapure water system with a conductivity of 18.2×10-6 cm /Ω. Analytical grade ethanol 99.95 % was used as purchased from Sigma Aldrich (St. Luis, MI).

3.2.1 Nanofluids

In this study, titanium oxide (IV) nanoparticles were used. Spherical, non-porous TiO₂ nanospheres of ca. 21 nm diameter were acquired from Sigma Aldrich (St. Luis, MI) in nanopowder form, with ≥99.5% trace metals basis. The nanofluid solutions were prepared at 0.1, 0.01 and 0.001 % w/v in ethanol, by dissolving the nanoparticles in an ultrasonic bath. The solutions with different concentrations by weight were prepared using a microbalance GR 202 with an accuracy of 0.00005 grams. In all these solutions, no additives such as surfactants or salts were added. Thereafter nanofluids were placed in an ultrasonic bath from Fisher Scientific (FB15047) for ca. 30 minutes, until no agglomeration was observed. Before each experiment, the solution was again sonicated in the ultrasonic bath for at least 30 minutes, in order to dissolve completely the nanoparticles agglomerates. Attention was paid to the temperature of the ultrasonic bath, since significant temperature increase can lead to a different solution concentration, as ethanol is a volatile solvent and significant amount of the solvent can evaporate.

3.3.3 Cleaning procedure

During the experiments with pure ethanol, the substrates could be re-used, after 30 minutes in the ultrasonic bath in deionised water or isobutanol. Subsequently, the substrates were dried with a nitrogen stream, in order to remove any dust or solvent. During the experiments with TiO₂ solutions, the substrate could not be re-used, since the removal of the nanoparticles from between the pillars was impossible to achieve without destroying the surface micro-pattern and coating. Due to this fact, special attention was paid during the nanofluid experiments to the location where droplets are deposited.

In this chapter a detailed description of the equipment as well as the experimental procedures were presented. Most of the experimental results are based on visual observations, either with SEM or optical techniques.

It is worth noting that for these observations, uncertainty in measurement is not relevant. Indeed measurements of the contact angle and droplets profile was merely for guidance on the wettability of the substrates.

Chapter 4: Droplets Shape Control through Patterning

4.1 Visual observations and wettability

This chapter presents the results of observations and measurements of sessile drops behaviour on structured (patterned) surfaces with various shapes and variable spacings for different sizes of drops. It was observed that the shape of structured as well as the spacing could affect the geometry formed by the drops and wettability characteristics. The chapter will be organised in three distinctive sections. The first section reports on the optical observations of the shape of drops of various sizes on different structured (patterned) substrates. The patterns range from square, circular, triangular to star-shaped.

The second section of the chapter focuses on observations of the three phase contact line. A precursor thin film was observed in some instances. This recorded and quantified for various substrates investigated.

The third section of the chapter presents an attempt to analyse the optical observation, see in section one and two. It reports on wettability of these drops in the initial stages and tried to quantify the effect of substrate structures on wetting contact lines.

4.1 Visual Observations

This first section presents the optical observations of the deposited drops on the various substrates. A top-down view is selected to access the shape formed by these drops and attempt to clarify the effect of the patterns and structures on the shape formed by these drops.

Table 4.1 shows the drops geometries formed on substrates decorated with square pillars of 5×5 μm² lateral dimensions. It could be noted that for larger spacing the drops adopt a more circular shape. As the spacing is decreased, there is a transition from symmetrical, circular drops to a well defined square and octagons. This trend however is less pronounced when the size of the drops is increased.

Table 4.1. Ethanol droplets of 1μL and 4 μL on Square Pillars with 5×5 μm² lateral dimensions

Pillar Spacing	Droplet Shape	1 μL Droplet Volume	4 μL Droplet Volume
5	Octagon, Thin liquid film present	1mm	1mm
10	Pseudo- octagon	1mm	1 mm
20	Pseudo- octagon	1mm	1 mm
40	Circle	1mm	1mm
80	Circle	1mm	1 mm

Table 4.2 presents observation for even larger drops. The conclusion is a confirmation of the previous trend, seen in Table 4.1 i.e. larger drops sizes tend to supress the formation of geometrical drops.

Table 4.2. Ethanol droplets of 7 μL and 10 μL on Square Pillars with 5×5 μm² lateral dimensions

Pillar Spacing	Droplet Shape	7 μL Droplet Volume	10 μL Droplet Volume
5	Octagon Thin liquid film present
10	Pseudo- octagon
20	Pseudo- octagon
		Scale 2mm	Scale: 2mm

Table 4.3 presents the same observations for larger pillars i.e. of 10×10 μm² lateral dimensions. The transition from circular to square (geometrical) drops occurs around 40 μm spacing. Also, it is concluded that larger pillar sizes tend to reduce the formation of square and geometrical drops.

Table 4.3. Ethanol droplets of 1 μL and 4 μL on Square Pillars with 10×10 μm² lateral dimensions

Pillar Spacing	Droplet Shape	1 μL Droplet Volume	4 μL Droplet Volume
5	Rectangular Thin liquid film present
10	Octagon, thin liquid film present
20	Octagon
40	Circle
80	Circle
160	Circle
		Scale 1mm	Scale: 3mm

Table 4.4 presents the results for much bigger pillars i.e. 20×20 μm² lateral dimensions. The conclusion from these observations is that for larger pillar much wider spacing is required to have a transition from circular to square and geometrical droplet shapes.

Table 4.4. Ethanol droplets of 1 μL and 4 μL on Square Pillars with 20×20 μm² lateral dimensions, pillar spacing 5 microns to 40 microns

Pillar Spacing	Droplet Shape	1 μL Droplet Volume	4 μL Droplet Volume
5	Pseudo-octagon, with spherical cap, thin film present
10	Pseudo-Octagon, thin liquid film present
20	Pseudo-Octagon
40	Pseudo-Octagon
		Scale: 1mm	Scale: 2mm

Table 4.5 explores larger spacing for the same structures presented in Table 4.4. The circular shape reported in Table 4.5 confirms the trend discussed in Table 4.4 i.e. at larger spacings only circular drops are observed.

Table 4.5 Ethanol droplets of 1 μL and 4 μL on Square Pillars with 20×20 μm² lateral dimensions, pillar spacing 80 microns to 320 microns

Pillar Spacing	Droplet Shape	1 μL Droplet Volume	4 μL Droplet Volume
80	Circle
160	Circle
320	Circle
		Scale: 1mm	Scale: 2mm

Table 5.6 presents he observations for the largest square pillars used in the present investigation i.e. 40×40 μm² lateral dimensions. The trends reported previously are confirmed for these sizes. The larger the square pillars get the larger spacing is required to generate geometrical drops.

Table 4.6 Ethanol droplets of 1 μL and 4 μL on Square Pillars with 40×40 μm² lateral dimensions, pillar spacing 5 microns to 40 microns

Pillar Spacing	Droplet Shape	1 μL Droplet Volume	4 μL Droplet Volume
5	Square, with spherical cap
10	Rectangular/ Circle with thin liquid film
20	Pseudo- octagon
40	Pseudo- Octagon
		Scale: 1mm	Scale: 2mm

Table 4.7 explore much wider pillars spacing for the same sizes as in Table 4.6. The trends described previously are indeed confirmed in these observations.

Table 4.7 Ethanol droplets of 1 μL and 4 μL on Square Pillars with 40×40 μm² lateral dimensions, pillar spacing 80 microns to 320 microns

Pillar Spacing	Droplet Shape	1 μL Droplet Volume	4 μL Droplet Volume
80	Circle
160
320
		Scale: 1mm	Scale: 2mm

Table 4.8 presents the data for circular pillars. Although a similar transition described previously is observed for the circular pillars, there no definite square geometry. The corners of the squares formed are rather blunt and not as sharp as in the case of rectangular pillars.

Table 4.8 Ethanol droplets of 1 μL and 4 μL on Circular Pillars with 10×10π μm² lateral dimensions, pillar spacing 5 microns to 40 microns

Pillar Spacing	Droplet Shape	1 μL Droplet Volume	4 μL Droplet Volume
5	Pseudo-octagon Thin liquid film present
10	Pseudo-octagon
20	Circle
40	Pseudo- Octagon
		Scale: 1mm	Scale: 2mm

Table 4.9 presents the results for larger circular pillars compared to Table 4.8. The conclusion is that the spacing required for the transition occurs at smaller spacings as the circular pillars size is increased.

Table 4.9 Ethanol droplets of 1 μL and 4 μL on Circular Pillars with 10×10π μm² lateral dimensions, pillar spacing 80 microns to 160 microns

Pillar Spacing	Droplet Shape	1 μL Droplet Volume	4 μL Droplet Volume
80	Circle
160	Circle
		Scale: 1mm	Scale: 2mm

Table 4.10 presents the observations for triangular shaped pillars. At wider spacings the drops adopt a circular shape. However at smaller spacings the drops tend to take geometrical shapes transitioning from octagons to square (rectangles). The shapes observed for these triangular pillars is quite different from the previous shapes (rectangular and circular).

Table 4.10 Ethanol droplets of 1 μL and 4 μL on Triangular Pillars with 0.5×10×10 μm² lateral dimensions, pillar spacing 5 microns to 40 microns

Pillar Spacing	Droplet Shape	1 μL Droplet Volume	4 μL Droplet Volume
5	Pseudo-octagon Thin liquid film present
10	Pseudo-octagon
20	Distorted Circle
40	Circle
		Scale: 1mm	Scale: 2mm

Table 4.11 explores much wider spacings for the triangular pillars shown in Table 4.10. These observations confirm the trend reported earlier i.e. as spacing increases, the drops tend to assume a more circular shapes.

Table 4.11 Ethanol droplets of 1 μL and 4 μL on Triangular Pillars with 0.5×10×10 μm² lateral dimensions, pillar spacing 80 microns to 160 microns

Pillar Spacing	Droplet Shape	1 μL Droplet Volume	4 μL Droplet Volume
80	Circle
160	Circle
		Scale: 1mm	Scale: 2mm

Table 4.12 presents he results for star-shaped pillars. It can be concluded that at wider spacing the drops adopt a circular shape. This is in agreement with other pillar shapes. As the spacing between the pillars is reduced, the drops start assuming geometrical shapes. These range from rectangular to square or undefined geometries.

Table 4.12 Ethanol droplets of 1 μL and 4 μL on 6-Star-shaped Pillars, pillar spacing 5 microns to 40 microns

Pillar Spacing	Droplet Shape	1 μL Droplet Volume	4 μL Droplet Volume
5	Rectangular
10	Pseudo-octagon
20	Distorted Circle
40	Circle
		Scale: 1mm	Scale: 2mm

Table 4.13 Ethanol droplets of 1 μL and 4 μL on 6- Star-shaped Pillars, pillar spacing 80 microns to 160 microns

Pillar Spacing	Droplet Shape	1 μL Droplet Volume	4 μL Droplet Volume
80	Circle
160	Circle
		Scale: 1mm	Scale: 2mm

4.2 Thin film observations

During the experimental study, it was observed on specific surfaces, along with the droplet a thin liquid film spreading beyond the contact line. This thin liquid film exhibited different dynamics from the droplet and therefore, the dynamics of this thin film was investigated with a microscope, in order to define the different stages of evaporation.

The surfaces examined are square pillars, with 5×5 μm² and 10×10 μm²lateral dimensions, and 5 to 10μm pillar spacing. The afore-mentioned surfaces were selected due to the thin liquid film observation and the variety in droplet shape. Observations related to the dynamics of droplets and thin films are presented in Table 4.14-4.17 below.

Table 4.14 Droplet (4 μL volume and square size) and thin film evaporation on Square Pillars, with 5×5 μm²lateral dimensions and 5 μm pillar spacing

Experimental time after droplet deposition	Observation
t=27s	Square droplet and square thin film
t=30s	Droplet evaporation from one side
t=32 s	Thin Film Evaporation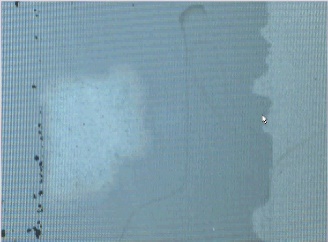
Scale	1mm

The observations reported in Table 4.14 show the main droplet acting as a reservoir whereas the thin film extend beyond the contact line of this latter. The main droplet seems to be feeding the thin film. After a while the thin film evaporates as seen after t=32 s.

Table 4.15 Droplet (4 μL volume and square size) and thin film evaporation on Square Pillars, with 5×5 μm² lateral dimensions and 10 μm pillar spacing

Experimental time after droplet deposition	Observation
t=18 s	Square thin film initially
t=23 s	Square film spreading stage
t=105 s	Thin Film Evaporation and depining stage
Scale	1mm

The observations in Table 4.15 give a hint on the dynamics of the thin film depinning and its interaction with the pillars. The contact line of the thin film seems to adopty the pattern of the pillars as it recedes.

Table 4.16: Droplet (4 μL volume and square size) and thin film evaporation on Square Pillars, with 10×10 μm² lateral dimensions and 5 μm pillar spacing

Experimental time after droplet deposition	Evaporation Stage
t= 24s	Square Droplet and square thin film
t=82 s	Droplet Evaporation from upper edge
t=85 s	Droplet and thin film Evaporation
Scale	1mm

Table 4.16 shows the depinning of the thin film (upper left corner). It demonstrates the random aspect of the depinning process.

Table 4.17 Droplet (4 μL volume and square size) and thin film evaporation on Square Pillars, with 10×10 μm² lateral dimensions and 10 μm pillar spacing

Experimental time after droplet deposition	Evaporation Stage
t=21 s	Circular Droplet and octagon-shaped thin film
t= 47s	Droplet Evaporation
t= 51s	Film Evaporation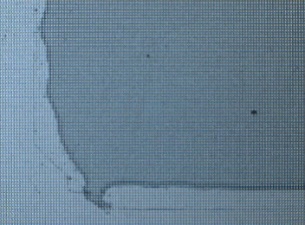
Scale	2 mm

Table 4.17 presents observations for circular droplets and corresponding extended thin film. The sequence clearly shows how the droplets feeds the thin film and gets depleted of liquid until it disappears as seen in frame at t=51 s. Once the thin film is deprived of the feeding reservoir which is the droplet, this latter depins following evaporation.

4.3 Wettability measurements

Chapter 5: Nanofluid droplets on structured

In the following chapter the deposits from evaporating drops on structured substrates is investigated. Deposits of nanoparticles from nanosuspensions comprising Titanium Oxide nanoparticles and ethanol as a base fluid is studied. The objective of this chapter is to compare the deposits at the contact line following dryout for various geometries as introduced in the previous chapter. The aim is to gain insight in how the various geometrical shapes affect the deposits following dryout. In particular we focus on deposition near sharp edges for the case of non-spherical drops.

The chapter is organised in two distinct parts. The first part presents optical observations obtained using an optical microscope. The second part of the chapter uses Scanning Electron Microscope (SEM) to gain further insight in the structuring of the deposits at the nanoscale.

5.1 Macroscopic observations of nanofluid droplets

In the following section, images of drops (and their corresponding deposits) on structured surfaces with square pillars with varying spacing are presented in the following tables.

Table 5.1: Visual observations of drops and their deposits on 5X5 square pillars with varying spacing for droplets of 4 L volume and TiO2 concentration of 0.01% per weight.

The first row in Table 5.1 shows the shape of the droplets of nanofluid in the initial stage as the spacing between pillars is increased. In agreement with the results presented in Chapter 4, the increase in the spacing leads to more circular shapes. On the other hand, geometrical shapes where observed as the spacing is reduced.

The second row of Table 5.1 shows the resulting deposits from the previously described experiments. The deposits seem to follow the same shapes described in the first row. This indicates that the nanoparticles deposit near the contact line as in previous studies about the coffee-stain effect.

The next set of experiments are conducted on the same pillar shape, but of increasing pillar size. These observations are presented in Table 5.2, from which it can be concluded that the increasing pillar size does not affect the deposit pattern and the droplet shape. There may be a subtle effect on the threshold of transition between circular and geometrical shapes. When comparing the effect of pillars size on droplet shapes, the pure fluid seems to be affected by this latter. However, when nanoparticles are added, the pillar size do not seem to drastically affect the geometrical shape formation.

Table 5.2: Visual observations of drops and their deposits on 10X10 square pillars with varying spacing for droplets of 4 L volume and TiO₂concentration of 0.01% per weight.

In Table 5.3 the results from the experiments on square pillars of 20X20 μm lateral dimensions are presented, where the same conclusion can be drawn. The pillar size does not affect the shape and the deposit pattern of the nanofluid, but the pattern is determined from the pillar shape and spacing only.

Table 5.3: Visual observations of drops and their deposits on 20X20 square pillars with varying spacing for droplets of 4 L volume and TiO₂ concentration of 0.001% per weight.

Table 5.4: Optical images showing the effect of TiO₂ concentration on 10X10 μm² square pillars, with 10 μm pillar spacing (droplet volume 4 Μl).

Table 5.4 shows the effect of concentration on both the shape of the droplets and the dried deposits. Although the general shape and geometry of the drop is not affect significantly by the present of particles, there some subtle effects noticed. The geometry of the drops is more defined and sharper with nanoparticles. At the highest concentration of 0.1%, the drops kept a square shape but a very clear spherical interface could be observed on top. Also, the highest concentration yielded a transition from pseudo-octagon shapes to a more defined square one.

5.2 SEM data for nanoparticles deposits near contact lines

The Scanning Electron Microscope (SEM) described in Chapter 3 was used to obtain images at the nanoscale of the deposits presented previously in Tables 5.1-5.3. Following the same structure as in Section 5.1, SEM images of deposits on square pillars of various sizes (5X5, 10X10 and 20X20 m) and various spacings (5-320 m) are presented in the following tables.

Table 5.5 shows the deposits from dried droplets as revealed by the SEM for the 5X5 μm pillars. It could be noted that in the case of circular droplets, the deposits are more concentrated near the contact line. On the other hand, in the case geometrical shapes, there are pronounced deposits in the centre.

Table 5.5: SEM for deposits on 5X5 square pillars with varying spacing for droplets of 4 μL volume and TiO2 concentration of 0.001% per weight.

Table 5.6 presents the same data for larger pillars i.e. 10X10 m. Again the concentration of deposits near the contact line for circular drops is highlighted. This occurs for larger spacings as introduced earlier.

Table 5.6: SEM for deposits on 10X10 square pillars with varying spacing for droplets of 4 μL volume and TiO2 concentration of 0.001% per weight.

Table 5.7 presents the images for the largest pillars i.e. 20X20 m. The same trends described for Tables 5.5 and 5.6 are confirmed for this case of largest pillars investigated.

Table 5.7: SEM for deposits on 20X20 square pillars with varying spacing for droplets of 4 μL volume and TiO2 concentration of 0.001% per weight

5.3 SEM data analysis

In this section, we will attempt to gain more insight into the deposits by exploiting the SEM data further. Higher magnification focusing on the deposits near the contact line are acquired. This would allow us to explore the structuring of individual nanoparticles and their interaction with the pillars.

The surface investigated with higher magnification is with square pillars of 10X10 μm² lateral dimensions and with 10μm pillar spacing.

Table 5.8 shows the deposits near the contact line on 10X10 μm² square pillars with 10μm spacing. The deposits as observed by the SEM at lower and higher magnifications is presented. The higher magnification reveals how the nanoparticles are arranged around the pillars. The first important observation is the top tip of the pillar does not seem to be coated with nanoparticles. These latter deposit on the surface and in between the pillars. As a general observation, the nanoparticles will align with the length of the pillars on the sides of the geometrical deposit. Near the corners on the hand, the nanoparticles grow diagonally to the pillars.

Table 5.8: SEM for deposits on 10X10 μm² square pillars with 10μm spacing for droplets of 4 μL volume and TiO2 concentration of 0.001% per weight

Figure 5.2 shows the 3D profile extracted from the SEM images to have a better idea on the profile of these deposits. It can observed that the nanoparticles seem to deposit and grow around the pillars.

Figure 5.1: 3D SEM simulation of TiO₂ deposits on 10X10 square pillars ,with 10 μm spacing, at the left bottom corner of the contact line

Figure 5.2 presents the profile of the deposit as measured by the SEM and gives an order of magnitude of the height of these deposits. On the right hand side of Figure 5.2, the height of these deposits is found to be of the order of c.a. 10 m. This is of the same order of magnitude as the pillars themselves.

Figure 5.2: Deposits at the left bottom corner of the contact line on a surface with 10X10 square pillars, 10 μm spacing.

Figure 5.3 presents similar data as in Figures 5.1. and 5.2 on the side of the geometrical deposit.

Figure 5.3: 3D SEM simulation of TiO₂ deposits on 10X10 square pillars, with 10 μm spacing, at the left side of the contact line.

The same observations highlighted before are found to be valid for the sides. The profile given by the SEM measurement as indicated on Figure 5.4 is of the same order as the pillars height i.e. 10 μm.

Figure 5.4: Deposits at the left side of the contact line, on 10X10 square pillars, 10 μm spacing.

To summarise, this chapter examined the deposition of nanoparticles from the geometrical drops as studied in Chapter 4. Both optical observation and more in depth SEM imaging were used to reveal the behaviour of the nanoparticles near the contact line of the evaporated droplets.

Chapter 6: Conclusions and outlooks

In this work surfaces were produced to generate regular structures and study wettability and evaporation of droplets. Silicon wafers were used in conjunction with microfabrication techniques to produce substrates exhibiting regular structures (pillars) of various size, spacing and geometry.

Following the fabrication of these substrates, the first objective was to study the wettability of pure liquid droplets on these latter. It was concluded that on substrates with structures with large spacing, droplets tend to assume a spherical shape. This is similar to what is observed on flat surfaces without any structures. However, when the spacing is reduced, the droplets tend to take more geometrical shapes including square, octagons and hexagons. The size of the pillars may also have an effect on the geometry of these droplets. It is however not independent of the spacing.

Furthermore, in many cases it was observed that a thin film, extending beyond the three phase contact line is formed. The formation of the thin film and its size is found to depend on the spacing between the pillars. To rationalize our observations, we suggest imbibition of the liquid between the pillars as a mechanism for the formation of this thin film. In addition, the evaporation of drops with the thin film deviates from the usual dynamics. Drops with the thin film tend to act as a reservoir where as most of the evaporation occurs on the interface of the thin film. This behaviour is not observed for spherical drops with no thin film, as most of the evaporation happens near the three phase contact line.

Contact angle measurements for spherical drops are also reported and attempts to measured wettability for geometrical drops was undertaken. This however turned to be challenging as the contact angle for non-spherical droplets is a local property.

Following the previous study on wettability and geometry effect on the structured substrates, the investigation aimed at studying deposits from nanofluid droplets on these very same substrates. Droplets of various sizes containing various concentration of nanoparticles were deposited the structured substrates and allowed to evaporate freely. The dried deposits were later studied by optical microscopy and SEM imaging. It was concluded that the nanoparticles tend to deposit near the three-phase contact line for all geometries. The deposits along the contact line however is not uniform. More concentration of particles is observed near the sharp edges where curvature is highest. This is in agreement with recent studies on geometrical droplets evaporation.

Further to optical observations, an SEM imaging approach was adopted. This revealed how nanoparticles organise themselves near the contact line and how they interacted with the pillars. A profile analysis of the deposits showed that these latter have the same height as the pillars.

The results presented in Chapter 4 and Chapter 5 are a selection from the overall data. More experiments were performed to confirm the same trends described earlier. To keep the thesis as concise as possible we presented the main data which show the observed behaviours.

The dynamics of the evaporation of these geometrical drops is worth further investigation. The evolution of the shape in time could present an experimental challenge. The thin film described in Chapter 4 can be studied further using more involved experimental techniques such interferometry. This might reveal further information on the dynamics of the thickness of the thin film as it evaporated.

References

Ning, D., Duong, B., Thomas, G., Qiao, Y., Ma, L., Wen, Q., Su, M. Mechanical and morphological analysis of cancer cells on nanostructured substrates. Langmuir, 2016. 32, 2718-2723.
Askounis, A., Takata, Y., Sefiane, K., Koutsos, V., Shanahan, M.E. “Biodrop” evaporation and ring-stain deposits: the significance of DNA length. Langmuir 2016, 32, 4361-4369.
Chen, S., Su, M., Zhang, C., Gao, M., Bao, B., Yang, Q., Su, B., Song, Y. Fabrication of nanoscale circuits on inkjet-printing patterned substrates. Adv. Matter 2015, 27, 3928-3933.
Xiao, R., Enright, R. & Wang, E. N. Prediction and optimization of liquid propagation in micropillar arrays. Langmuir 2010,26, p. 15070-15075.
Barthlott, W., Neinhuis, C. (1997) Purity of the sacred lotus, or escape from contamination in biological surfaces. Planta 1997, 202(1), p. 1-8.
Gao, X., Jiang, L., Biophysics: water repellent legs of water striders. Nature 2004, 432, p. 36-36.
Jiang, L., Zhao, Y., Zhai, J. A lotus-leaf-like superhydrophobic surface: a porous microsphere/nanofiber composite film prepared by electrohydrodynamics. Angew. Chemie. 2004, 43, p. 4338-4341.
Wu, A., Yu, L., Li, Z., Yang, H., Wang, E. Atomic force microscope investigation of large-circle DNA molecules. Anal. Biochem. 2004, 325, p. 293−300.
Chang, S. T., Velev, O. D. Evaporation-induced particle microseparations inside droplets floating on a chip. Langmuir 2006, 22, p. 1459−1468.
Sefiane, K. On the Formation of Regular Patterns from Drying Droplets and Their Potential Use for Bio-Medical Applications. Journal of Bionic Engineering 2010, 7, p. S82-S93.
Brutin, D., et al. Pattern formation in drying drops of blood. Journal of Fluid Mechanics 2011, 667, p. 85-95.
Young, T., An Essay on the Cohesion of Fluids. Philosophical Transactions of the Royal Society of London, 1805. 95: p. 65-87.
Joanny, J.F. and P.G. de Gennes, A model for contact angle hysteresis. The Journal of Chemical Physics, 1984. 81(1): p. 552-562.
de Gennes, P.G., Wetting: statics and dynamics. Reviews of Modern Physics, 1985. 57(3): p. 827-863.
Xia, Y. and G.M. Whitesides, Soft lithography. Annual review of materials science, 1998. 28(1): p. 153-184.
Squires, T.M. and S.R. Quake, Microfluidics: Fluid physics at the nanoliter scale. Reviews of modern physics, 2005. 77(3): p. 977-1026.
Reiter, G., Dewetting of thin polymer films. Physical Review Letters, 1992. 68(1): p. 75-78.
N. Gudris, L. Kulikowa, Die Verdampfung kleiner Wassertropfen, Zeitschrift Für Phys. 25 (1924) 121–132.
R.F. Mangel, E. Baer, The evaporation of water drops from a “Teflon” surface, Chem. Eng. Sci. 17 (1962) 705–706.
R.D. Deegan, O. Bakajin, T.F. Dupont, G. Huber, S.R. Nagel, T.A. Witten, Capillary flow as the cause of ring stains from dried liquid drops, Nature. 389 (1997) 827–829. doi:10.1038/39827.
R. Deegan, O. Bakajin, T. Dupont, G. Huber, S. Nagel, T. Witten, Contact line deposits in an evaporating drop, Phys. Rev. E. 62 (2000) 756–765. doi:10.1103/PhysRevE.62.756.
R.D. Deegan, Pattern formation in drying drops, Phys. Rev. E. 61 (2000) 475–485. doi:10.1103/PhysRevE.61.475.
K. Sefiane, Patterns from drying drops., Adv. Colloid Interface Sci. 206 (2014) 372–81.
X. Zhong, A. Crivoi, F. Duan, Sessile nanofluid droplet drying, Adv. Colloid Interface Sci. 217 (2015) 13–30.
C.H. Chon, S. Paik, J.B. Tipton, K.D. Kihm, Effect of Nanoparticle Sizes and Number Densities on the Evaporation and Dryout Characteristics for Strongly Pinned Nanofluid Droplets, Langmuir. 23 (2007) 2953–2960.
D. Brutin, Influence of relative humidity and nano-particle concentration on pattern formation and evaporation rate of pinned drying drops of nanofluids, Colloids Surfaces A Physicochem. Eng. Asp. 429 (2013) 112–120.
T. Still, P.J. Yunker, A.G. Yodh, Surfactant-Induced Marangoni Eddies Alter the Coffee-Rings of Evaporating Colloidal Drops, Langmuir. 28 (2012) 4984–4988.
X. Zhong, F. Duan, Evaporation of Sessile Droplets Affected by Graphite Nanoparticles and Binary Base Fluids, J. Phys. Chem. B. 118 (2014) 13636–13645.
M. Parsa, S. Harmand, K. Sefiane, M. Bigerelle, Evaporation of Binary Mixture Nanofluid Drops: Pattern Formation, in: M. Laudon, F. Case, B. Romanowicz (Eds.), 10th Annu. TechConnect World Innov. Conf., TechConnect, Washington, 2016: pp. 196–197.
M. Parsa, R. Boubaker, S. Harmand, K. Sefiane, M. Bigerelle, R. Deltombe, Patterns from dried water-butanol binary-based nanofluid drops, J. Nanoparticle Res. 19 (2017) 268.
A. Askounis, K. Sefiane, V. Koutsos, M.E.R. Shanahan, The effect of evaporation kinetics on nanoparticle structuring within contact line deposits of volatile drops, Colloids Surfaces A Physicochem. Eng. Asp. 441 (2014) 855–866..
M. Parsa, S. Harmand, K. Sefiane, M. Bigerelle, R. Deltombe, Effect of Substrate Temperature on Pattern Formation of Nanoparticles from Volatile Drops, Langmuir. 31 (2015) 3354–3367.
S.U.S. Choi, J.A. Eastman, Enhancing thermal conductivity of fluids with nanoparticles, in: ASME Int. Mech. Eng. Congr. Expo., ASME, San Fransisco, 1995: pp. 99–105.
C.T. Nguyen, G. Roy, C. Gauthier, N. Galanis, Heat transfer enhancement using Al2O3–water nanofluid for an electronic liquid cooling system, Appl. Therm. Eng. 27 (2007) 1501–1506.
J. Barber, D. Brutin, L. Tadrist, A review on boiling heat transfer enhancement with nanofluids., Nanoscale Res. Lett. 6 (2011) 1–16.
R.A. Taylor, P.E. Phelan, T.P. Otanicar, C.A. Walker, M. Nguyen, S. Trimble, R. Prasher, Applicability of nanofluids in high flux solar collectors, J. Renew. Sustain. Energy. 3 (2011) 23104.
D. Peer, J.M. Karp, S. Hong, O.C. Farokhzad, R. Margalit, R. Langer, Nanocarriers as an emerging platform for cancer therapy, Nat. Nanotechnol. 2 (2007) 751–760.
M.J. Kao, C.H. Lo, T.T. Tsung, Y.Y. Wu, C.S. Jwo, H.M. Lin, Copper-oxide brake nanofluid manufactured using arc-submerged nanoparticle synthesis system, J. Alloys Compd. 434–435 (2007) 672–674.
H. Sirringhaus, T. Kawase, R.H. Friend, T. Shimoda, M. Inbasekaran, W. Wu, E.P. Woo, High-Resolution Inkjet Printing of All-Polymer Transistor Circuits, Science (80-. ). 290 (2000) 2123–2126.
T. Kawase, H. Sirringhaus, R.H. Friend, T. Shimoda, Inkjet printed via-hole interconnections and resistors for all-polymer transistor circuits, Adv. Mater. 13 (2001) 1601–1605.
B.J. De Gans, P.C. Duineveld, U.S. Schubert, Inkjet Printing of Polymers: State of the Art and Future Developments, Adv. Mater. 16 (2004) 203–213.
B. Dan, T.B. Wingfield, J.S. Evans, F. Mirri, C.L. Pint, M. Pasquali, I.I. Smalyukh, Templating of Self-Alignment Patterns of Anisotropic Gold Nanoparticles on Ordered SWNT Macrostructures, ACS Appl. Mater. Interfaces. 3 (2011) 3718–3724.
T. Yakhno, Salt-induced protein phase transitions in drying drops., J. Colloid Interface Sci. 318 (2008) 225–30.
K. Sefiane, On the Formation of Regular Patterns from Drying Droplets and Their Potential Use for Bio-Medical Applications, J. Bionic Eng. 7 (2010) S82–S93.
H.M. Gorr, J.M. Zueger, D.R. McAdams, J.A. Barnard, Salt-induced pattern formation in evaporating droplets of lysozyme solutions, Colloids Surfaces B Biointerfaces. 103 (2013) 59–66.
A. Bar-Cohen, M. Arik, M. Ohadi, Direct Liquid Cooling of High Flux Micro and Nano Electronic Components, Proc. IEEE. 94 (2006) 1549–1570.
X. Zhang, J. Wang, L. Bao, E. Dietrich, R.C.A. van der Veen, S. Peng, J. Friend, H.J.W. Zandvliet, L. Yeo, D. Lohse, Mixed mode of dissolving immersed nanodroplets at a solid–water interface, Soft Matter. 11 (2015) 1889–1900. doi:10.1039/C4SM02397H.
A.K. Panwar, S.K. Barthwal, S. Ray, Effect of evaporation on the contact angle of a sessile drop on solid substrates, J. Adhes. Sci. Technol. 17 (2003) 1321–1329. doi:10.1163/156856103769172760.
K.S. Birdi, D.T. Vu, A. Winter, A study of the evaporation rates of small water drops placed on a solid surface, J. Phys. Chem. 93 (1989) 3702–3703. doi:10.1021/j100346a065.
H. Hu, R.G. Larson, Evaporation of a Sessile Droplet on a Substrate, J. Phys. Chem. B. 106 (2002) 1334–1344. doi:10.1021/jp0118322.
H.Y. Erbil, G. McHale, M.I. Newton, Drop Evaporation on Solid Surfaces: Constant Contact Angle Mode, Langmuir. 18 (2002) 2636–2641. doi:10.1021/la011470p.
G. McHale, S.M. Rowan, M.I. Newton, M.K. Banerjee, Evaporation and the Wetting of a Low-Energy Solid Surface, J. Phys. Chem. B. 102 (1998) 1964–1967. doi:10.1021/jp972552i.
R.. Picknett, R. Bexon, The evaporation of sessile or pendant drops in still air, J. Colloid Interface Sci. 61 (1977) 336–350. doi:10.1016/0021-9797(77)90396-4.
M.E.R. Shanahan, Simple Theory of “Stick-Slip” Wetting Hysteresis, Langmuir. 11 (1995) 1041–1043. doi:10.1021/la00003a057.
D. Orejon, K. Sefiane, M.E.R. Shanahan, Stick–Slip of Evaporating Droplets: Substrate Hydrophobicity and Nanoparticle Concentration, Langmuir. 27 (2011) 12834–12843. doi:10.1021/la2026736.
A. Askounis, Surface nano-patterning using the coffee-stain effect, Univeristy of Edinburgh, 2014.
W. Sempels, R. De Dier, H. Mizuno, J. Hofkens, J. Vermant, Auto-production of biosurfactants reverses the coffee ring effect in a bacterial system, Nat. Commun. 4 (2013) 1757. doi:10.1038/ncomms2746.
H. Hu, R.G. Larson, Analysis of the Microfluid Flow in an Evaporating Sessile Droplet, Langmuir. 21 (2005) 3963–3971. doi:10.1021/la047528s.
R. Chen, L. Zhang, D. Zang, W. Shen, Wetting and Drying of Colloidal Droplets: Physics and Pattern Formation, in: M.M. Rahman, A.M. Asiri (Eds.), Adv. Colloid Sci., InTech, 2016: pp. 3–25. doi:10.5772/65301.
H. Hu, R.G. Larson, Analysis of the effects of Marangoni stresses on the microflow in an evaporating sessile droplet., Langmuir. 21 (2005) 3972–3980. doi:10.1021/la0475270.
C.A. Ward, F. Duan, Turbulent transition of thermocapillary flow induced by water evaporation, Phys. Rev. E. 69 (2004) 56308. doi:10.1103/PhysRevE.69.056308.
J.-H. Kim, S.-B. Park, J.H. Kim, W.-C. Zin, Polymer Transports inside Evaporating Water Droplets at Various Substrate Temperatures, J. Phys. Chem. C. 115 (2011) 15375–15383. doi:10.1021/jp202429p
V. Dugas, J. Broutin, E. Souteyrand, Droplet Evaporation Study Applied to DNA Chip Manufacturing, Langmuir. 21 (2005) 9130–9136. doi:10.1021/la050764y.
J. Park, J. Moon, Control of Colloidal Particle Deposit Patterns within Picoliter Droplets Ejected by Ink-Jet Printing, Langmuir. 22 (2006) 3506–3513. doi:10.1021/la053450j.
H. Hu, R.G. Larson, Marangoni Effect Reverses Coffee-Ring Depositions, J. Phys. Chem. B. 110 (2006) 7090–7094. doi:10.1021/jp0609232.
M. Majumder, C.S. Rendall, J.A. Eukel, J.Y.L. Wang, N. Behabtu, C.L. Pint, T.-Y. Liu, A.W. Orbaek, F. Mirri, J. Nam, A.R. Barron, R.H. Hauge, H.K. Schmidt, M. Pasquali, Overcoming the “Coffee-Stain” Effect by Compositional Marangoni-Flow-Assisted Drop-Drying, J. Phys. Chem. B. 116 (2012) 6536–6542. doi:10.1021/jp3009628.
A.K. Thokchom, Q. Zhou, D.-J. Kim, D. Ha, T. Kim, Characterizing self-assembly and deposition behavior of nanoparticles in inkjet-printed evaporating droplets, Sensors Actuators B Chem. 252 (2017) 1063–1070. doi:10.1016/j.snb.2017.06.045.
D.M. Kuncicky, O.D. Velev, Surface-Guided Templating of Particle Assemblies Inside Drying Sessile Droplets, Langmuir. 24 (2008) 1371–1380. doi:10.1021/la702129b.
J.R. Moffat, K. Sefiane, M.E.R. Shanahan, Effect of TiO2 nanoparticles on contact line stick−slip behavior of volatile drops, J. Phys. Chem. B. 113 (2009) 8860–8866. doi:10.1021/jp902062z.
R. Bhardwaj, X. Fang, P. Somasundaran, D. Attinger, Self-assembly of colloidal particles from evaporating droplets: Role of DLVO interactions and proposition of a phase diagram, Langmuir. 26 (2010) 7833–7842. doi:10.1021/la9047227.
T.P. Bigioni, X.-M. Lin, T.T. Nguyen, E.I. Corwin, T. a Witten, H.M. Jaeger, Kinetically driven self assembly of highly ordered nanoparticle monolayers, Nat. Mater. 5 (2006) 265–270. doi:10.1038/nmat1611.
Y. Li, Q. Yang, M. Li, Y. Song, Rate-dependent interface capture beyond the coffee-ring effect, Sci. Rep. 6 (2016) 24628. doi:10.1038/srep24628
K. Uno, K. Hayashi, T. Hayashi, K. Ito, H. Kitano, Particle adsorption in evaporating droplets of polymer latex dispersions on hydrophilic and hydrophobic surfaces, Colloid Polym. Sci. 276 (1998) 810–815. doi:10.1007/s003960050314.
X. Shen, C.-M. Ho, T.-S. Wong, Minimal Size of Coffee Ring Structure, J. Phys. Chem. B. 114 (2010) 5269–5274. doi:10.1021/jp912190v.
H. Kim, F. Boulogne, E. Um, I. Jacobi, E. Button, H.A. Stone, Controlled Uniform Coating from the Interplay of Marangoni Flows and Surface-Adsorbed Macromolecules, Phys. Rev. Lett. 116 (2016) 124501. doi:10.1103/PhysRevLett.116.124501.
C. Seo, D. Jang, J. Chae, S. Shin, Altering the coffee-ring effect by adding a surfactant-like viscous polymer solution, Sci. Rep. 7 (2017) 500. doi:10.1038/s41598-017-00497-x.
D. Orejon, A Study of Nanosuspension Droplets Free Evaporation and Electrowetting, University of Edinburgh, 2013.
K. Sefiane, On the role of structural disjoining pressure and contact line pinning in critical heat flux enhancement during boiling of nanofluids, Appl. Phys. Lett. 89 (2006) 44106. doi:10.1063/1.2222283.
M. Anyfantakis, D. Baigl, Manipulating the Coffee-Ring Effect: Interactions at Work, ChemPhysChem. 16 (2015) 2726–2734. doi:10.1002/cphc.201500410.
J. Wu, J. Xia, W. Lei, B. Wang, Generation of the smallest coffee-ring structures by solute crystallization reaction on a hydrophobic surface, RSC Adv. 3 (2013) 5328. doi:10.1039/c3ra40465j.
J.R. Moffat, K. Sefiane, M.E.R. Shanahan, Nanofluid Droplet Evaporation Kinetics and Wetting Dynamics on Flat Substrates, J. Nano Res. 7 (2009) 75–80. doi:10.4028/www.scientific.net/JNanoR.7.75.
E. Adachi, A.S. Dimitrov, K. Nagayama, Stripe Patterns Formed on a Glass Surface during Droplet Evaporation, Langmuir. 11 (1995) 1057–1060. doi:10.1021/la00004a003.
A. Crivoi, F. Duan, Fingering structures inside the coffee-ring pattern, Colloids Surfaces A Physicochem. Eng. Asp. 432 (2013) 119–126. doi:10.1016/j.colsurfa.2013.04.051.
Y.-F. Li, Y.-J. Sheng, H.-K. Tsao, Evaporation Stains: Suppressing the Coffee-Ring Effect by Contact Angle Hysteresis, Langmuir. 29 (2013) 7802–7811. doi:10.1021/la400948e.
T.A.H. Nguyen, M.A. Hampton, A. V Nguyen, Evaporation of Nanoparticle Droplets on Smooth Hydrophobic Surfaces: The Inner Coffee Ring Deposits, J. Phys. Chem. C. 117 (2013) 4707–4716. doi:10.1021/jp3126939
M.E. Buzoverya, Y.P. Shcherbak, I. V Shishpor, Quantitative estimation of the microstructural inhomogeneity of biological fluid facies, Tech. Phys. 59 (2014) 1550–1555. doi:10.1134/S1063784214100119.
H.H. Lee, S.C. Fu, C.Y. Tso, C.Y.H. Chao, Study of residue patterns of aqueous nanofluid droplets with different particle sizes and concentrations on different substrates, Int. J. Heat Mass Transf. 105 (2017) 230–236. doi:10.1016/j.ijheatmasstransfer.2016.09.093.
X. Zhong, H. Xie, F. Duan, Deposition patterns from evaporating sessile droplets with suspended mixtures of multi-sized and multi-species hydrophilic and non-adsorbing nanoparticles, Appl. Therm. Eng. 111 (2017) 1565–1572. doi:10.1016/j.applthermaleng.2016.08.040.
Y. Choi, J. Han, C. Kim, Pattern formation in drying of particle-laden sessile drops of polymer solutions on solid substrates, Korean J. Chem. Eng. 28 (2011) 2130–2136. doi:10.1007/s11814-011-0084-7.
E.L. Talbot, A. Berson, P.S. Brown, C.D. Bain, Drying and Deposition of Picolitre Droplets of Colloidal Suspensions in Binary Solvent Mixtures, in: NIP28 28th Int. Conf. Digit. Print. Technol. Digit. Fabr., Society for Imaging Science and Technology: Springfield, Quebec, 2012: pp. 420–423.
Papadopoulos et al., Wetting on the microscale: Shape of a Liquid drop on a Microstructured Surface at different Length Scales, Langmuir 28 (2012), pp8392-8398.
Yong,X., Zhang, L.T., Nanoscale wetting on groove-Patterned Surfaces, Langmuir 2009, 25 (9), 5045-5053.
Courbin, L. et al., Imbibition by polygonal spreading on microdecorated surfaces, Nature Letters 2007, 6, pp. 661-664
Blow, M.L., Yeomans, J.M., Anisotropic imbibition on surfaces patterned with polygonal posts, Phil. Trans. R. Soc. A (2011), 369, pp. 2519-2527.
Raj, R. et al., High-resolution liquid patterns via three-dimensional droplet shape control, Nat. Commun. 2014 (5:4975), pp. 1-8
Denkov, N et al., Self-shaping of oil droplets via the formation of intermediate rotator phases upon cooling,Nature 2015 (528), pp. 392–395
Courbin, l. et al., Imbibition by polygonal spreading on microdecorated surfaces, Nature Materials 2007 ,6, pp. 661–664
Chu, K-H., Xiao, R., Wang, E.N., Uni-directional liquid spreading on asymmetric nanostructured surfaces, Chu, Nature Materials 2010, 9(5), pp.413-417

Share this: Facebook Twitter Reddit LinkedIn WhatsApp

Cite This Work

To export a reference to this article please select a referencing stye below:

Related Services

View all

Dissertation Writing Service

From £136

Dissertation Proposal Writing Service

From £124

Female student reading and using laptop to study

Topics and Titles Writing Service

From £24

DMCA / Removal Request

If you are the original writer of this dissertation and no longer wish to have your work published on the UKDiss.com website then please:

Dissertation Services

PhD Services

Other Services

Contact

Table of Content

Chapter 1: Introduction and applications