Verification of the Certificate Using the BLS Signature Scheme
Info: 9901 words (40 pages) Dissertation
Published: 16th Dec 2019
Tagged: Computer Science
1 INTRODUCTION
1.1 Introduction to MANETs
MANET known as Mobile Ad-Hoc Network is a self-organised, dynamic and infrastructure less network. MANET consists of mobile nodes that roam freely, every node has its own range of signal communication, other nodes within the range can interact and exchange messages. New nodes join and some other nodes may leave or some nodes fail to connect as they move out of the MANET network range.
The nodes in MANET are energy constrained, i.e., nodes are battery powered devices. There are many security threats to MANETS such as Denial of Service, Eavesdropping, Interception and Routing Attacks.
From the very beginning, the use of MANETS has been appealing to both military and civilian applications. MANETS are also characterized by being bandwidth and energy constrained.
As an example of MANET, let us consider multiplayer computer games. With the increasing number of mobile devices, multiplayer games are getting very popular. In such games, the set of players is changing during the games, the players can join or leave the game at any time, there are different teams, etc. In some of them, the decision about the player admission or game strategy is taken only when a certain number of members agree. Some transmitted information has to be protected (encrypted) against other players or teams.
MANETS are a kind of Wireless ad-hoc networks (WANET) that usually has a routable networking environment on top of a Link Layer ad hoc network. MANETS consist of a peer-to-peer, self-forming, self-healing network.
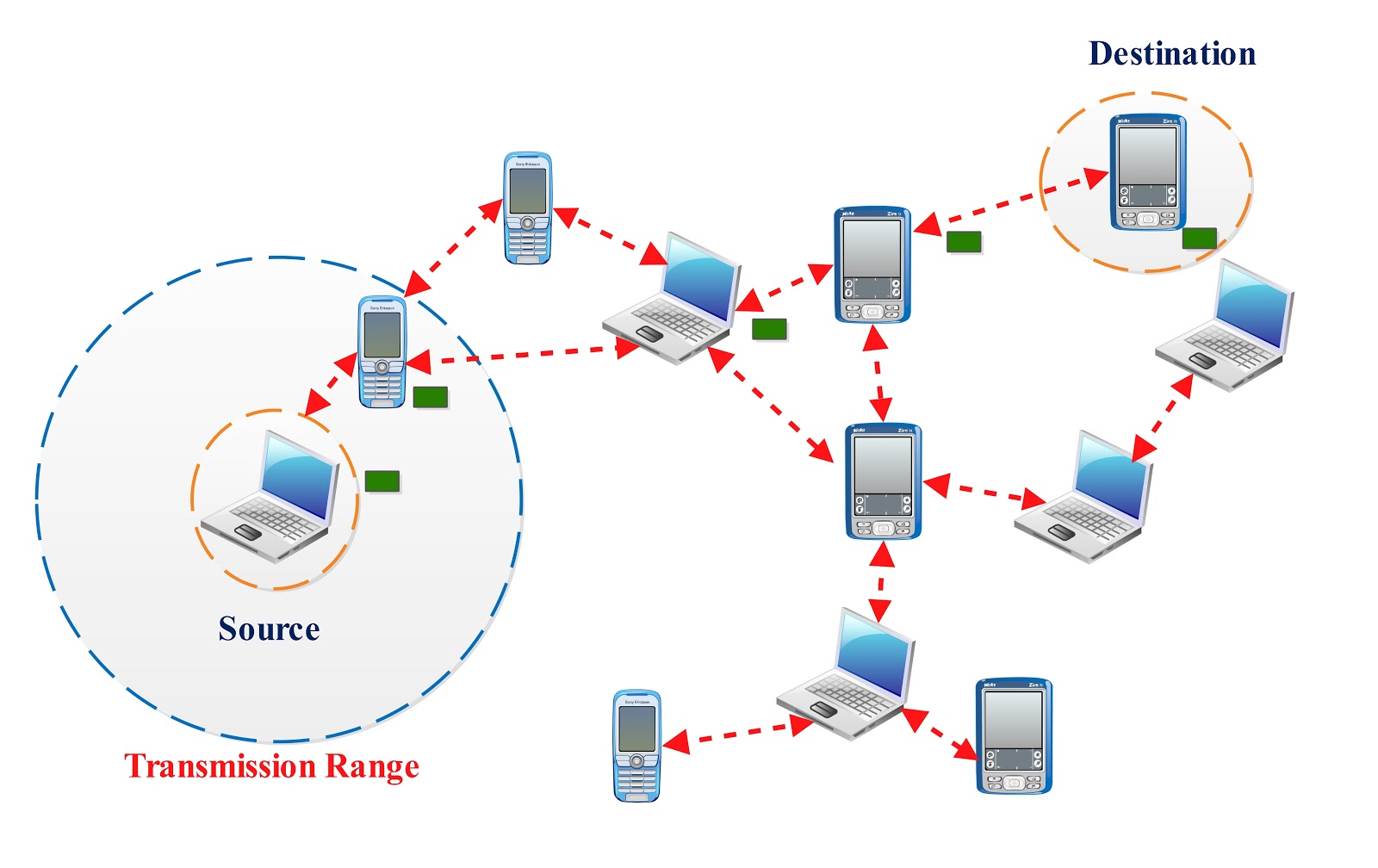
Figure 1.1.a : Mobile ad-hoc network
1.2 Types of MANETs
- Vehicular ad-hoc networks (VANETs) are used for communication between vehicles and road side equipment. Intelligent vehicular ad-hoc networks(InVANETs) are a kind of artificial intelligence that helps vehicles to behave in intelligent manners during vehicle-to-vehicle collisions and accidents.
- Smart phone ad-hoc networks (SPANs) leverage the existing hardware (primarily Bluetooth and Wifi) in commercially available smart phones to create peer-to-peer networks without relying on cellular carrier networks, wireless access points, or traditional network infrastructure. SPANs support multi-hop relays and there is no notion of a group leader so peers can join and leave at will without destroying the network.
- Internet-based mobile ad-hoc networks (iMANETs) are ad hoc networks that link mobile nodes and fixed Internet-gateway nodes.
- Military or Tactical MANETs are used by military units with emphasis on security, range and integration with existing systems.

Figure 1.2.a : Types of Mobile ad-hoc networks
1.3 Applications of MANET
With the increase of portable devices as well as progress in wireless communication, ad-hoc networking is gaining importance with the increasing number of widespread applications in the commercial, Military and private sectors. Mobile Ad-Hoc networks allow users to access and exchange information regardless of their geographic position or proximity to infrastructure. In contrast to infrastructure networks, all nodes in MANETs are mobile and their connections are dynamic. Unlike other mobile networks, MANETs do not require a fixed infrastructure. This offers advantageous decentralized character to network. Decentralization makes the networks more flexible and more robust.
- Military Sector: Military equipment now routinely contains some sort of computer equipment. Ad-Hoc networking would allow the military to take advantage of commonplace technology to maintain an information network between soldiers, vehicles and military information headquarters. The basic techniques of ad hoc network came from this field.
- Data Networks: A commercial application for MANETs includes ubiquitous computing. By allowing computers to forward data for others, data networks may be extended far beyond the usual reach of installed infrastructure. Networks may be made more widely available and easier to use.
- Low Level: Appropriate low level application might be in home networks where devices can communicate directly to exchange information. Similarly, in other civilian environments like taxi cab, sports stadium, boat and small aircraft, mobile ad hoc communications will have many applications.
- Sensor Networks: This technology is a network composed of a very large number of small sensors. These can be used to detect any number of properties of an area. Examples include temperature, pressure, toxins, pollutions etc. The capabilities of each sensor are very limited, and each must rely on others in order to forward the data to a central computer. Individual sensors are limited in their computing ability and are prone to failure and loss. Mobile ad-hoc sensor networks could be the key to future homeland security.
1.4 Challenges in MANET
A. Autonomous: No centralized administration entity is available to manage the operation of the different mobile nodes.
B. Dynamic Topology: Nodes are mobile and can be connected dynamically in an arbitrary manner. Links of the network vary timely and are based on the proximity of one node to another node.
C. Device Discovery: Identifying relevant newly moved in nodes and informing about their existence need dynamic update to facilitate automatic optimal route selection.
D. Bandwidth Optimization: Wireless links have significantly lower capacity than the wired links. Routing protocols in wireless networks always use the bandwidth in an optimal manner by keeping the overhead as low as possible. The limited transmission range also imposes a constraint on routing protocols in maintaining the topological information. Especially in MANETS due to frequent changes in topology, maintaining the topological information at all nodes involves more control overhead which, results in turn in more bandwidth wastage.
E. Limited Resources: Mobile nodes rely on battery power, which is a scarce resource. Also, storage capacity and power are severely limited.
F. Scalability: Scalability can be broadly defined as whether the network is able to provide an acceptable level of service even in the presence of a large number of nodes.
G. Limited Physical Security: Mobility implies higher security risks such as peer-to-peer network architecture or s shared wireless medium accessible to both legitimate network users and malicious attackers. Eavesdropping, spoofing, denial of service attacks should be considered.
H. Infrastructure-less and self-operated: Self-healing feature demands MANET should realign itself to blanket any node moving out of its range.
I. Poor Transmission Quality: This is an inherent problem of wireless communication caused by several error sources that result in degradation of the received signal.
J. Ad Hoc Addressing: Challenges in standard addressing scheme to be implemented.
K. Network Configuration: The whole MANET infrastructure is dynamic and is the reason for dynamic connection and disconnection of the variable links.
L. Topology Maintenance: Updating information of dynamic links among nodes in MANETS is a major challenge.
1.5 Attacks on MANET
Securing wireless ad-hoc networks is a highly challenging issue. Understanding possible form of attacks is always the first step towards developing a good security solution. Security of communication in MANET is important for secure transmission of information. Absence of any central co-ordination mechanism and shared wireless medium makes MANET more vulnerable to digital or cyber- attacks than wired network there a number of attacks that affect MANET.
An honest node can also be compromised if it is under the control of the attacker. As the network comprises of layers of protocols, the attacks are specific to a layer and the security should also be implemented in the corresponding layer. These attacks can be classified as:

Figure 1.5.a : MANET Layer specific attacks
Attacks on Mobile Ad-Hoc networks (MANETs) can be classified into following two categories:
1) Passive Attack
2) Active Attack
1.5.1 Passive Attack:
In this type of attack, the intruder only performs some kind of monitoring on certain connections to get information about the traffic without injecting any fake information. This type of attack serves the attacker to gain information and makes the footprint of the invaded network in order to apply the attack successfully. The types of passive attack are eavesdropping, traffic analysis and snooping.
- Eavesdropping: This is a passive attack. The node simply observes the confidential information. This information can later be used by the malicious node. The secret information like location, public key, private key, password etc. can be fetched by the eavesdropper.
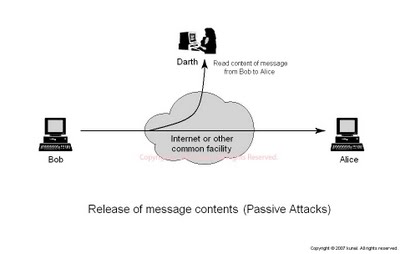
Figure 1.5.1.a: Eavesdropping
- Traffic Analysis: In MANETs the data packets as well as the traffic pattern, both are important for adversaries. For example, confidential information about network topology can be derived by analysing traffic patterns. Traffic analysis can also be conducted as active attack by destroying nodes, which simulates self-organization in the network, and valuable data about the topology can be gathered.
Figure 1.5.1.b Traffic Analysis
- Snooping: Snooping is unauthorized access to another person’s data. It is similar to Eavesdropping but is not necessarily limited to gaining access to data during its transmission. Snooping can include casual observance of an e-mail that appears on another’s computer screen or watching someone else typing. More sophisticated snooping uses software programs to remotely monitor activity on a computer or network device. Malicious hackers (crackers) frequently use snooping techniques to monitor key strokes, capture passwords and login information and to intercept e-mail and other private communications and data transmissions. Corporations sometimes snoop on employees legitimately to monitor their use of business computers and track internet usage. Governments may snoop on individuals to collect information and prevent crime and terrorism. Although snooping has a negative aspect in general but in computer technology snooping can refer to any program or utility that performs a monitoring function.
1.5.2 Active Attack:
In this type of attack, the intruder performs an effective violation on either the network resources or the data transmitted. This is done by International Journal on New Computer Architectures and their Applications causing routing disruption, network resources depletion, and node breaking. In the following are the types of active attacks over MANET and how the attacker’s threat can be performed:
- Flooding Attack: In flooding attack, attacker exhausts the network resources, such as bandwidth and to consume a node’s resources, such as computational and battery power or to disrupt the routing operation to cause severe degradation in network performance. For example, in AODV protocol, a malicious node can send a large number of RREQs in a short period to a destination node that does not exist in the network. Because no one will reply to the RREQs, these RREQs will flood the whole network. As a result, all of the node battery power, as well as network bandwidth will be consumed and could lead to denial-of-service.
- Black hole Attack: Route discovery process in AODV is vulnerable to black hole attack. The mechanism, that is, any intermediate node may respond to RREQ message if it has a fresh enough route, devised to reduce routing delay, is used by the malicious node to compromise the system. In this attack, when a malicious node listens to a route request packet in the network, it responds with the claim of having the shortest and the freshest route to the destination node even if no such route exists. As a result, the malicious node easily misroute network traffic to it and then drop the packets transitory to it.
- Wormhole Attack: In a wormhole attack, an attacker receives packets at one point in the network, “tunnels” them into another point in the network, and then replays them into the network from that point. Routing can be disrupted when routing control message are tunnelled. This tunnel between two colluding attacks is known as wormhole. In DSR, AODV, this attack could prevent discovery of any routes and may create a wormhole even for packet not addressed to itself because of broadcasting. Wormholes are hard to detect.
- Gray hole attack: This attack is also known as routing misbehaviour attack which leads to dropping of messages. Gray hole attack has two phases. In the first phase the node advertise itself as having a valid route to destination while in second phase, nodes drops intercepted packets with a certain probability.
- Link spoofing attack: In a link spoofing attack, a malicious node advertises fake links with non-neighbours to disrupt routing operations. For example, in the OLSR protocol, an attacker can advertise a fake link with a target’s two hop neighbours. This causes the target node to select the malicious node to be its MPR. As an MPR node, a malicious node can then manipulate data or routing traffic. For example, modifying or dropping the routing traffic or performing other types of DoS attacks.
- Malicious code attacks: Malicious code attacks include viruses, worms, spywares and trojan horses, can attack both operating system and user application. Repudiation attacks: Repudiation refers to a denial of participation in all or part of the communication. Many of encryption mechanisms and firewalls used at different layer are not sufficient for packet security. Application layer firewalls may take into account in order to provide security to packets against many attacks. For example, spyware detection software has been developed in order to monitor mission critical services.
- Session Hijacking: Attacker in session hijacking takes the advantage to exploits the unprotected session after its initial setup. In this attack, the attacker spoofs the victim’s nodes IP address, finds the correct sequence number i.e., expected by the target and then launches various DoS attacks. In session hijacking, the malicious nodes tries to collect secure data (passwords, secret keys, logos, names etc.) and other information from nodes. Session hijacking attacks are also known as address attack which make effect on OLSR protocol. The TCP-ACK storm problem may occur when malicious node launches a TCP session hijacking attack.
- SYN Flooding Attack: The SYN Flooding attacks are the type of Denial of Service (DoS) attacks, in which the attacker creates a large number of half opened TCP connections with victim node. These half opened connections are never complete the handshake to fully open the connection.
- Denial of service attack: Denial of service attacks are aimed at complete disruption of routing information and therefore the whole operation of ad-hoc network.
- Jamming: Jamming is a special class of DoS attacks which are initiated by malicious node after determining the frequency of communication. In this type of attack, the jammer transmits signals along with security threats. Jamming attacks also prevent the reception of legitimate packets.
- Traffic monitoring and analysis: Traffic monitoring and analysis can be deployed to identify the communication parties and functionalities, which could provide information to launch further attacks. Since these attacks are not specific to the MANET, other wireless networks, such as the cellular network, satellite network and WLAN also suffer from these potential vulnerabilities.
Figure 1.5.2.a : Active and Passive Attacks
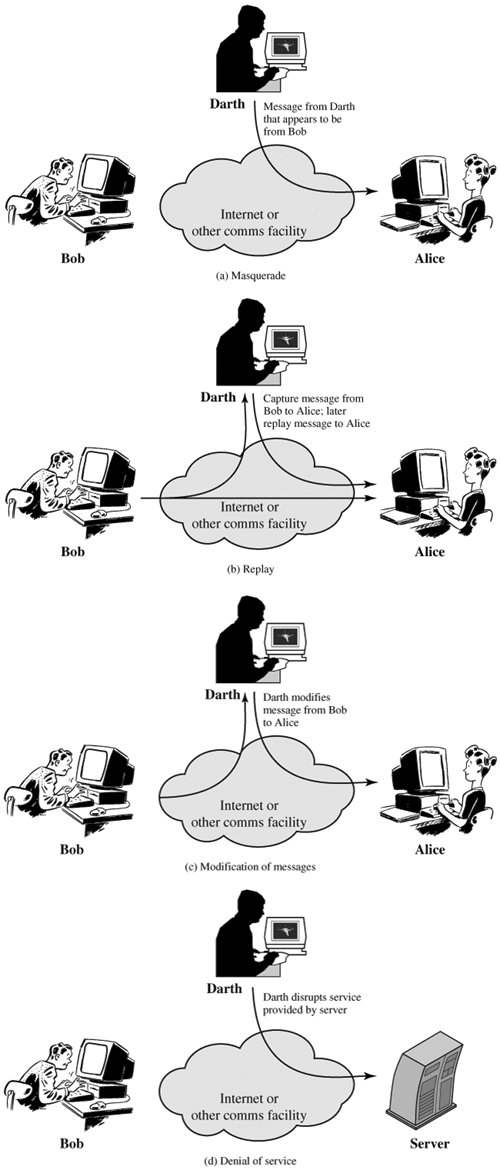
Figure 1.5.2.b:Active Attacks
1.6 Distributed Public Key Infrastructure (PKI)
1.6.1 Public Key Cryptography
Public Key Cryptography, or Asymmetric Cryptography, is any cryptographic system that uses pairs of keys: public keys which may be disseminated widely, and private keys which are known only to the owner. This accomplishes two functions: Authentication, which is when the public key is used to verify that a holder of the private key send the message, and Encryption, whereby the holder of the paired private key can decrypt the message encrypted with the public key.
Public Key Cryptography provides many security services like Confidentiality, Integrity, Authentication, Non-repudiation, Encryption and Digital Signatures.
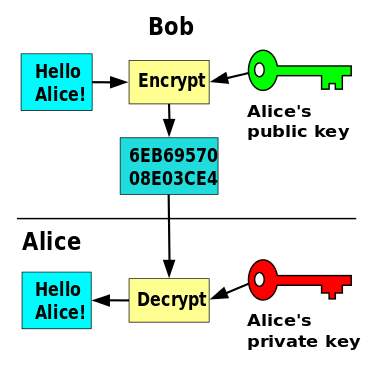
Figure 1.6.1.a : Public Key Encryption
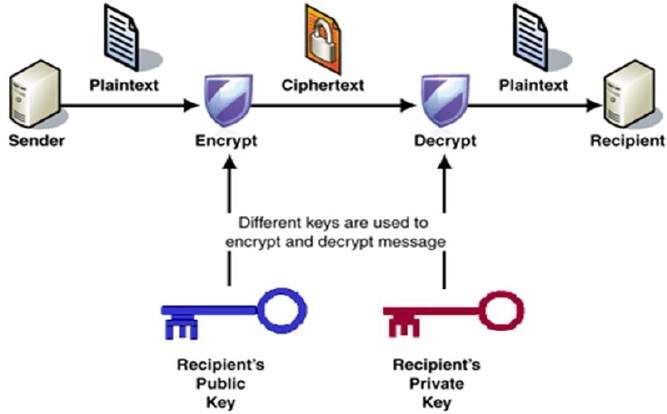
Figure 1.6.1.b : Public Key Cryptography
1.6.2 Public Key Infrastructure
A Public Key Infrastructure is a set of roles, policies, and procedures needed to create, manage, distribute, use, store and revoke digital certificates and manage public key encryption. The purpose of a PKI is to facilitate the secure electronic transfer of information for a wide range of electronic activities such as e-commerce, internet banking and confidential email. It is required for activities where simple passwords are an inadequate authentication method and more rigorous proof is required to confirm the identity of the parties involved in communication and to validate the information being transferred.
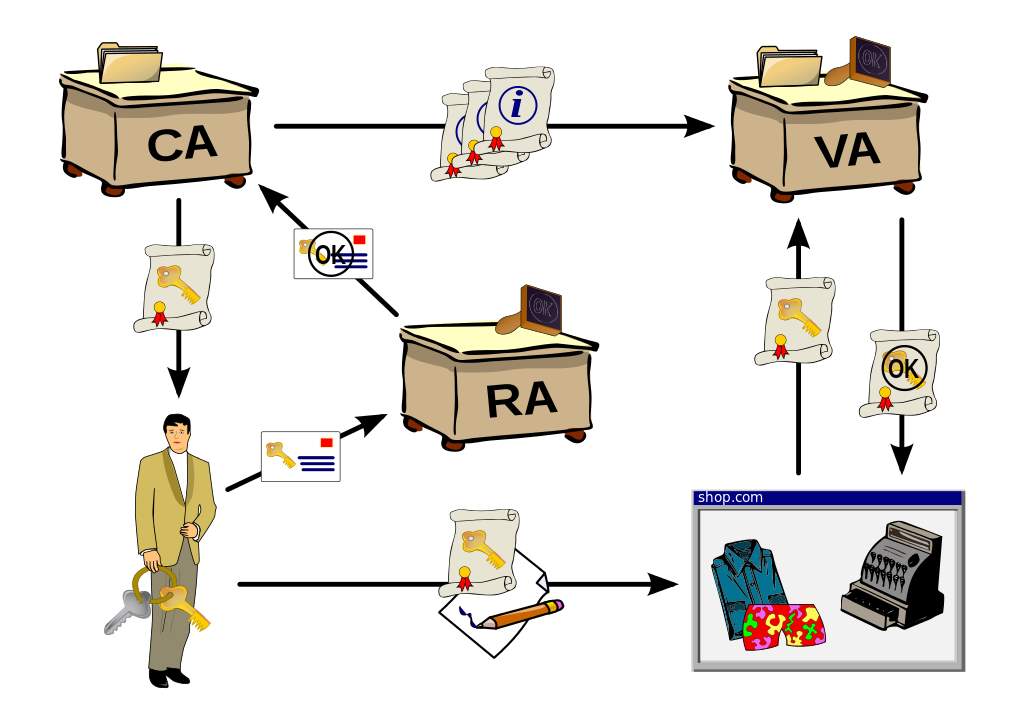
Figure 1.6.2.a : Diagram of a Public Key Infrastructure
Public Key Infrastructure helps in securing the communication using authentication and encryption through digital certificates and public key cryptography respectively. The distributed PKI approach is adopted in the case of MANETs to make the network completely decentralised.
Public Key Infrastructure(PKI) manages digital certificates which are important in the deployment of public key cryptography. In PKI Environment, Certificate Authority(CA) issues and maintains the certificates of participating entities, the certificate contains the public key and ID of the entity, the CA signs the certificate using the master secret key s and this certificate can be verified by using the master public key PK.
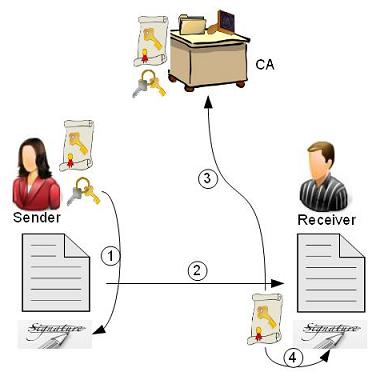
Figure 1.6.2.a : PKI Process Flow
Generally, in a PKI environment, a certificate authority(CA) issues and manages the public key certificates of the participating entities, the CA uses a master secret key s to sign the certificate.
In MANETS, we cannot adopt the same PKI, as the network is dynamic and infrastructure less. So, the role of CA needs to be distributed to the nodes i.e., the master secret key s is to be shared among different nodes and the master secret key can only be generated if at least the threshold number of secrets are pooled together.
General PKI is not suitable for MANET as we cannot assign the sole power of CA to a single node because of its dynamic and changing topology i.e., the node with CA functionality may break down or move out of the MANET range, which results in the non-availability of CA.
To achieve the distributed PKI environment for MANETS, we use a (t,n) threshold scheme that distributes the power of CA , i.e., we have to distribute the master secret key s to nodes of the MANET.
In this project, we discuss how a threshold number of nodes sign a certificate and the verification of the certificate can be done by any node using the BLS signature scheme.
1.7 Threshold Cryptography
As MANET is a decentralized network, the master secret key s of the PKI is distributed among the nodes using secret sharing techniques.
One of the popular and most widely used secret sharing schemes is the Shamir’s secret sharing technique. In this scheme, the dealer distributes a secret s among n users. Each user receives it’s share privately from the dealer. To reconstruct a secret, it uses (t,n) threshold access structure, where t out of n shares are required.
Shamir’s secret sharing scheme can be adopted in MANETS. Even the role of the dealer can be played by the nodes of MANET itself. This is achieved by using a bivariate polynomial.
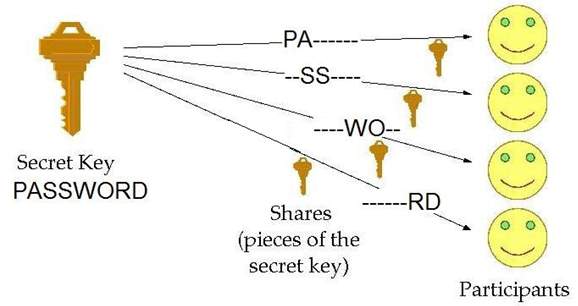
Figure 1.7.a:Example for secret sharing
1.8 Related Work
One common issue faced by MANET when applying cryptography is, how to distribute the role of CA or Trusted authority, many proposals use secret sharing technique to distribute secret key s of CA or trusted authority to secure MANET.
Zhou and Haas were the first to propose distributed CA for MANETS. They used threshold cryptography to distribute the role of the Certification Authority (CA) in a PKI scenario among a set of selected servers. However, this proposal is not suitable for a purely ad-hoc environment as these selected nodes may not always be available. Kong et al adapted a similar idea to distribute trust among all the nodes. However, their specific RSA threshold scheme has been proved insecure.
Shamir secret sharing technique is the most widely used secret sharing technique. We show that Shamir secret sharing technique along with the use of bi-variate polynomial helps to distribute the secret of CA among all nodes of MANET.
In other works, Bivariate Polynomials have already been used to dynamically allow new nodes joining the network without the need of any external trusted party. This technique is the result of inspiration from the original work of Anzai et al and Herranz et al constructed decentralized, flexible, dynamic group key distribution schemes by using polynomials in two variables. The goal is to generate common group secret keys. Saxena et al used similar technique to establish pairwise keys in a non-interactive way for a mobile ad-hoc scenario.
2 CONCEPTS AND PRELIMINARIES
2.1 Group and Field
Consider the traditional number systems
- N= {0,1,2….} the natural numbers
- Z= {m-n | m,n ⍷ N} the integers
- Q= {m/n}| m,n ⍷ Z, n6=0} the rational number
- R the real numbers
- C the complex numbers
For which we have N ⸦ Z ⸦ Q ⸦ R ⸦ C
- Algebraic Systems: A set ‘A’ with one or more binary(closed) operations defined on it is called an algebraic system.
Ex: (N, +), (Z,+, -), (R,+, . , -) are algebraic systems.
- Binary Operation: The binary operator * is said to be a binary operation
( closed operation) on a non empty set A, if
a*b IN A for all alb IN A (Closure Property)
Ex: The set N is closed with respect to addition and multiplication
but not w.r.t subtraction and division.
Properties
- Associativity: Let * be binary operation on a set A.
The operation * is said to be associative in A if
(a*b)*c = a*(b*c) for all a,b,c in A
- Identity: For an algebraic system ( A,*), an element ‘e’ in A is said to be an identity elect of A if
a*e = e*a = a for all a IN A.
- Note: For an algebraic system (a,*), the identity element, if exists is unique.
- Inverse: Let (A,*) be an algebraic system with identity ‘e’. Let a be element in A. An element b is said to be inverse of A if
a*b = b*a = e.
Semi Groups
- Semi Group: An algebraic system (A,*) is said to be a semi group if
1. * is closed operation on A.
2. * is an associative operation, for all a,b,c in A.
- Ex. (N,+) is a semi group.
- Ex. (N, .) is a semi group.
- Ex. (N, -) is not a semi group.
Monoid:
An algebraic system (A,*) is said to be a monoid if the following conditions are satisfied.
1. * is a closed operation in A.
2. * is an associative operation in A.
3. There is an identity in A.
- Ex. Show that the set ’N’ is a mooned with respect to multiplication.
- Solution: Here, N = {1,2,3,4,…..}
1. Closure Property: We know that product of two natural number is again a natural number.
i.e, a.b = b.a for all a,b in N
Multiplication is a closed operation.
2. Associativity: Multiplication of natural numbers is associative.
i.e, (a.b).c = a.(b.c) for all a,b,c in N
3. Identity: We have, 1 in N such that
a.1=1.a = a for all a in N.
Identity element exists, and 1 is the identity element.
Hence, N is a monoid with respect to multiplication.
Groups
- Group: An algebraic system (G,*) is said to be a group if the following conditions are satisfied.
1. * is a closed operation
2. * is an associative operation.
3. There is an identity in G.
4. Every element in G has inverse in G.
- Abelian group (Commutative group): A group (G,*) is said to be abelian ( or commutative) if
a*b = b*a “a,b IN G.
Properties:
- In a group (G,*) the following properties hold good
1. Identity element is unique
2. Inverse of an element is unique
3. Cancellation laws hold good.
a*b = a*c ⍴ b=c (left cancellation law)
a*c = b*c ⍴ a=b ( right cancellation law)
4. (a*b)-1 = b-1 * a-1
- In a group, the identity emergent is its own inverse.
- Order of a group :The number of events in a group is called order of the group.
- Finite group: If the order of a group G is finite, then G is called a finite group.
Ex. Show that, the set of all integers in a abelian group with
respect to addition.
- Solution: Let Z = set of all integers.
Let a,b,c are any three elements of Z
1. Closure Property: We know that, the Sum of two integers is again an integer.
i.e, a+b IN Z for all a,b in Z.
2. Associativity: We know that addition of integers is associative.
i.e, (a+b)+c = a+(b+c) for all a,b,c, in Z.
3. Identity: We have 0 in Z and a+0= a for all a IN Z. Identify elements exists, and ‘0’ is the identity element.
4. Inverse: To each a in Z, we have -a in Z such that a+(-a)= 0
5. Commutativity: We know that addition of integers is commutative
i.e, a + b = b + a for all a,b in Z.
Hence, (Z,+) is an abelian group.
Ex. Show that set of all non zero real number is a group with respect to multiplication.
Solution: Let R+ = set of all non zero real numbers.
Let a,b,c are any three events of R+
1. Closure Property: We know that, product of two non zero real numbers is
again a non zero real number.
i.e, a.b IN R+ for all a,b in R+
2. Associativity: We know that multiplication of real number is associative.
i.e, (a.b).c = a.(b.c) for all a,b,c in R+
3. Identity: We have 1 in R+ for all a.1= a for all a in R+
Identity element exists, and “1” is the identity element.
4. Inverse: To each a in R+ , we have 1/a in R+ such that
a.(1/a) = 1 i.e, Each element in R+ has an inverse.
5. Commutativity: We know that multiplication of real numbers is commutative.
i.e, a.b = b.a for all a,b in R+
Hence, (R+, . ) is an abelian group.
Note: Show that set of all real numbers “R” is not a group with respect to
multiplication
Solution: We have 0 in R,
The multiplication inverse of 0 does not exist.
Hence, R is not a group.
Finite Groups
- Ex. Show that G = {1,-1} is an abelian group under multiplication.
- Solution: The composition table of G is
1 -1
1 1 -1
-1 -1 1
1. Closure Property: Since all the entries of the composition table are the events of the given set, the set G is closed under multiplication.
2. Associativity: The elements of G are real numbers, and we know that
multiplication of real numbers is associative.
3. Identity: Here, 1 is the identity element and 1IN G.
4. Inverse: From the composition table, we see that the inverse elements of 1 and -1 are 1 and -1 respectively.
Hence, G is a group w.r.t multiplication.
5. Commutativity: The corresponding rows and columns of the table are
identical. Therefore, the binary operation is commutative.
Hence, G is an abelian group w.r.t multiplication.
Ex. Show that G = {1, -1, i, -i } is an abelian group under multiplication.
Solution: The composition table of G is
1 -1 i -i
1 1 -1 i -i
-1 1 1 -i i
i i -i -1 1
-i -i i 1 -1
1. Closure property: Since all the entries of the composition table are the elements of the given set, the set G closed under multiplication.
2. Associativity: The events of G are complex number, and we know that multiplication of complex numbers is associative.
3. Identity: Here, 1 is the identity element and
4. Inverse: From the composition table, we see that the inverse elements of
1,-1,i,-i are 1,-1,-i, i respectively.
5. Commutativity: The corresponding rows and columns of the table are identical. Therefore the binary operation. is commutative.
Hence, (G,.) is an abelian group.
Modulo Systems
- Addition modulo m (+m)
- Let m is a positive integer. For any two position integers a and b
- a + mb = a + b , if a + b < m
- a + mb = r if a = b2m
- where r is the remainder obtained by dividing (a=b) with m.
- Multiplication modulo p
- Let p is a positive integer. For any two positive integers a and b
- a p b = a b if a b < p
- a p b = r if a b 3 p where r is the remainder obtained by dividing (ab) with p.
- Ex 3 x5 4 = 2 , 5 x5 4 = 0, 2 x5 2 = 4
- In a group with 2 elements, each event is its own inverse
- In a group of even order, there will be at least one element (other than identity element) which is its own inverse
- The set G= { 0,1,2,3,4,…….m-1} is a group with respect to addition modulo m.
- The set G={1,2,3,4….p-1} is a group with respect to multiplication
modulo p, where p is a prime number.
- Order of a element of a group:
- Let (G,*) be a group. Let ‘a’ be an element of G. The smallest integer n such that an – e is called order of ‘a’. If no such number exists then the order is infinite .
Field:
If a ring <R, +, . >
is commutative
has the unity
every non-zero element of R has the inverse under the . operation.
Commutative ring with unity in which every non-zero element has a multiplication inverse.
Examples
1. <Q,+,x>, Q is a set of rational nos and binary operations + and x.
2. <R,+,x>, R is a set of real nos, and binary operations + and x.
3. <C,+,x>, C is a set of complex nos and binary operations + and x.
4. <Z,+,x>, Z is a set of integers and binary operations + and x is not a field as Z does not contain multiplication inverse of all its non-zero elements.
Finite Fields:
In mathematics, a finite field or Galois field is a field that contains a finite number of elements. As with any field, a finite field is set on which the operations of multiplication, addition, subtraction and division are defined and satisfy certain basic rules. The most common examples of finite fields are given by the integers mod p when p is a prime number.The number of elements of a finite field is called its order. A finite field of order q exists if and only if the order q is a prime power pk (where p is a prime number and k is a positive integer). All fields of a given order are isomorphic. In a field of order pk, adding p copies of any element always results in zero; that is, the characteristic of the field is p.
In a finite field of order q, the polynomial Xq-X has all q elements of the finite field as roots. The non-zero elements of a finite field form a multiplicative group. This group is cyclic, so all non-zero elements can be expressed as powers of a single element called primitive element of the field (in general there will be several primitive elements for a given field).A field has, by definition, a commutative multiplication operation. A more general algebraic structure that satisfies all the other axioms of a field but isn’t required to have a commutative multiplication is called a division ring (or sometimes skewfield). A finite division ring is a finite field by Wedderburn’s little theorem.
2.2 Elliptic Curves:
An elliptic curve is a curve that is also naturally a group.
- The group law is constructed geometrically.
- Elliptic curves have (almost) nothing to do with ellipses, so put ellipses and conic sections out of your thoughts.
- Elliptic curves appear in many diverse areas of mathematics, ranging from number theory to complex analysis, and from cryptography to mathematical physics.
Points on Elliptic Curves
Elliptic curves can have points with coordinates in any field such as Fp, Q, R.
- Elliptic curves with points in Fp are finite groups.
- Elliptic Curve Discrete Logarithm Problem (ECDLP) is the discrete logarithm problem for the group of points on an elliptic curve over a finite field.
- The best known algorithm to solve the ECDLP is exponential, which is why elliptic curve groups are used for cryptography.
The equation of an Elliptic Curve
An elliptic curve is a curve given by an equation of the form y2 = x2 + Ax + B
There is also a requirement that the discriminant ∆ = 4A3 + 27B2 is non-zero.
Equivalently, the polynomial x3 + Ax + B has distinct roots. This ensures that the curve is non-singular. O, that is “at infinity”, so E is the set E = { (x,y) : y2 = x2 + Ax + B } U {O}.
We can use geometry to make the points of an elliptic curve into a group.
The geometry of Elliptic Curves
The elliptic curve E : y2 = x3 – 5x + 8
Adding two points on the curve
Starts with points P, Q on E
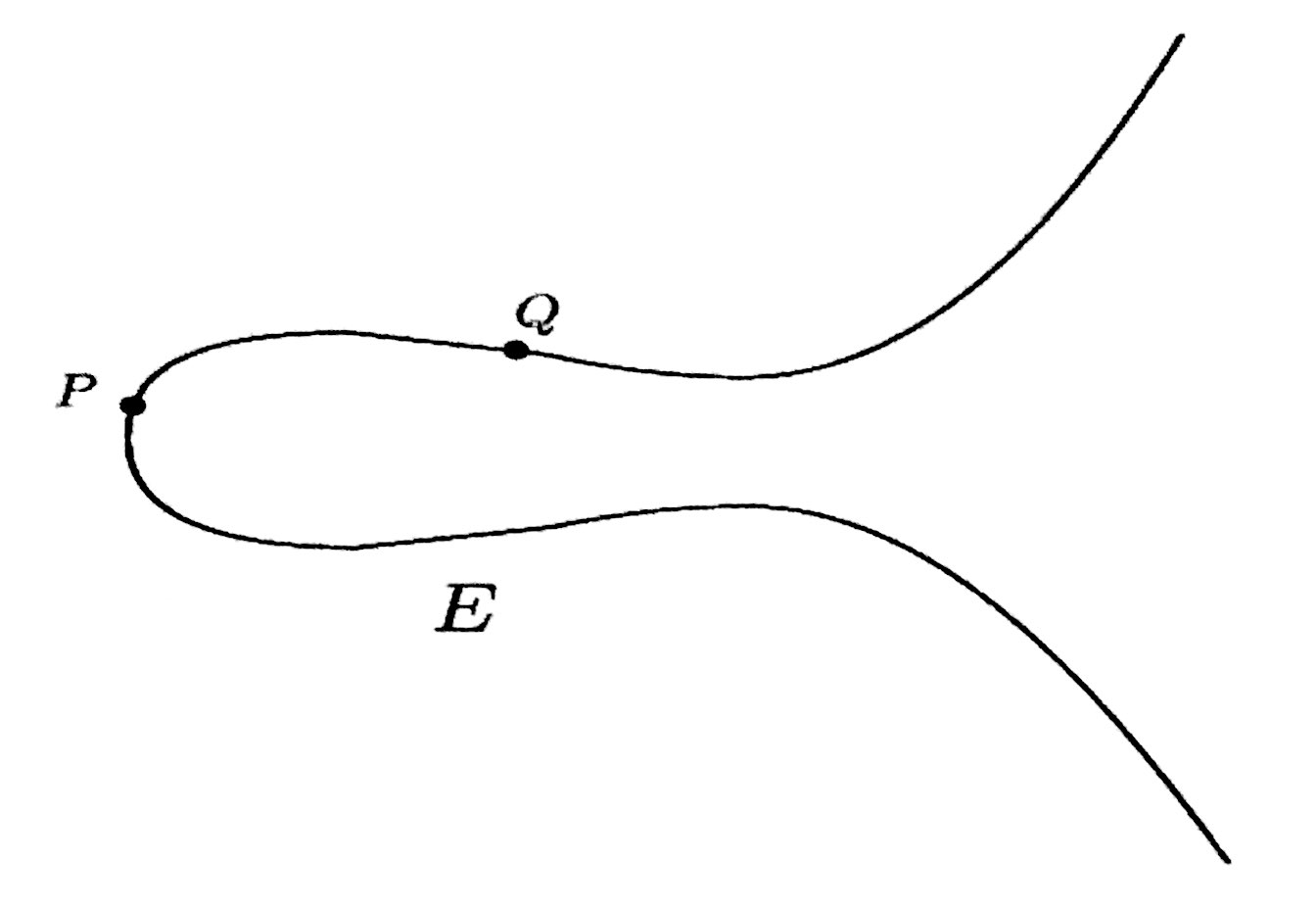
Draw the line L through P & Q
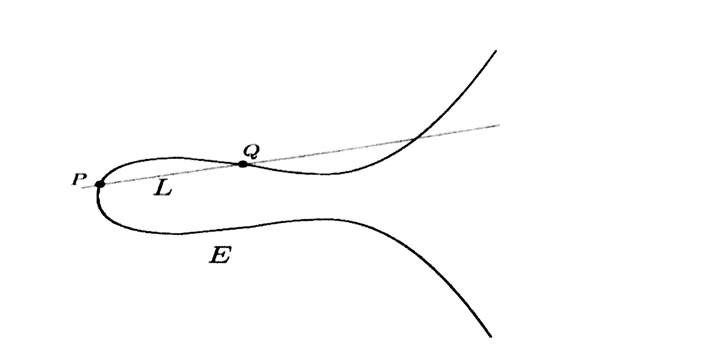
The Line L intersects the cubic curve E in a third point.
Call that third point R.
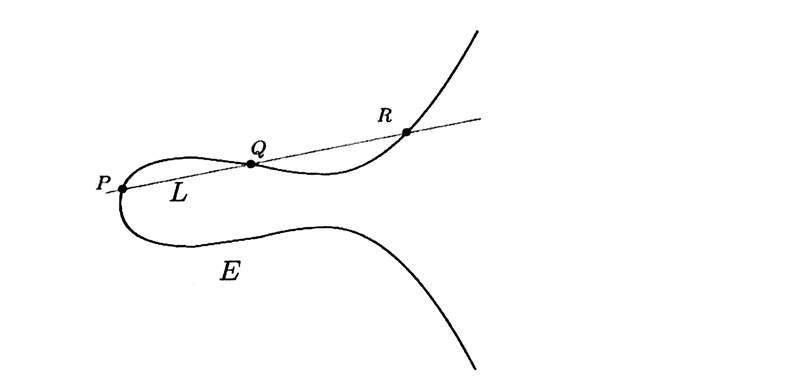
Draw the vertical line through R.
This vertical line hits E in another point.
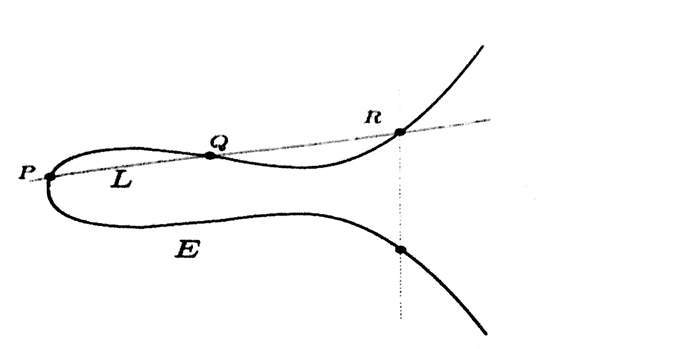
We define the sum of P and Q on E to be the reflected point.
We denote it by P + Q
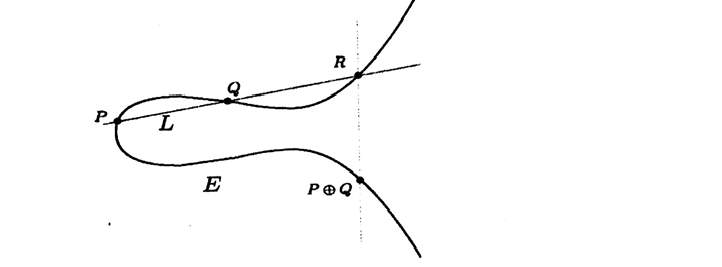
How do we add a point P to itself since there are many different lines that go through P ?
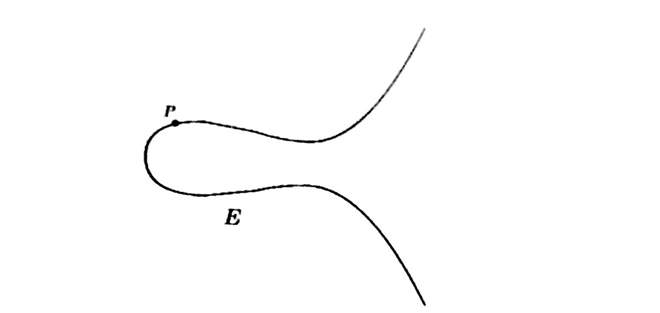
Adding a point to itself on an Elliptic Curve
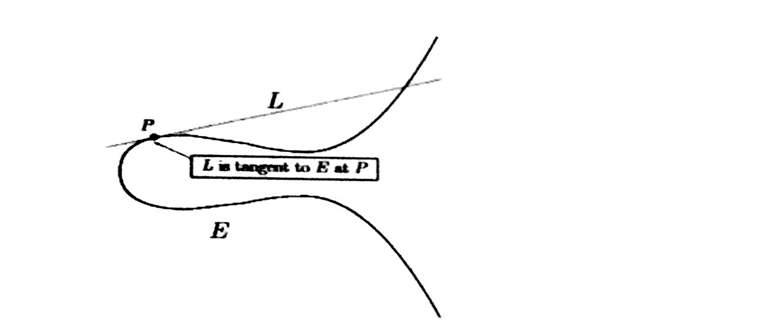
If we think of adding P to Q and let Q approach P , then the line L becomes the tangent line to E at P
Then we take the third intersection point R, reflect across the x-axis and call the resulting point 2P
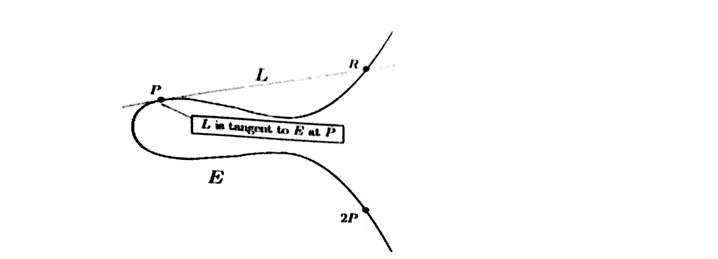
Vertical Lines and the extra point “At Infinity”
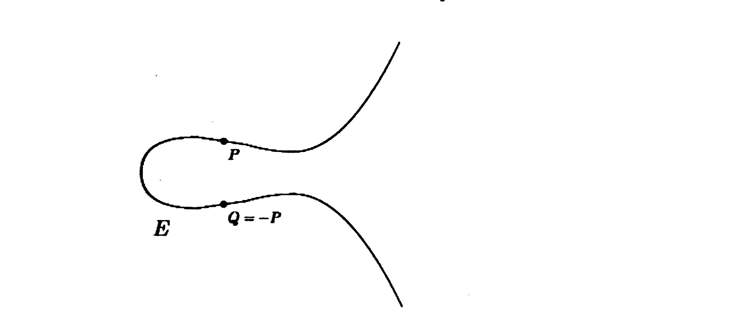
Let P € E.
We denote the reflected point by -P
The Algebra of Elliptic Curves
In other words, the addition law + makes the points of E into a commutative group.
All of the group properties are trivial to check except for the associative law ©. The associative law can be verified by a lengthy computation using explicit formulas, or by using more advanced algebraic or analytic methods.
Properties of “Addition” on E
Theorem: The addition law on E has the following properties:
(a) P + O = O + P = P for all P
N2.<x,z>=PolynomialRing(F1,2,order=’lex’)
N3.<x,z>=PolynomialRing(F1,2,order=’lex’)
N4.<x,z>=PolynomialRing(F1,2,order=’lex’)
N5.<x,z>=PolynomialRing(F1,2,order=’lex’)
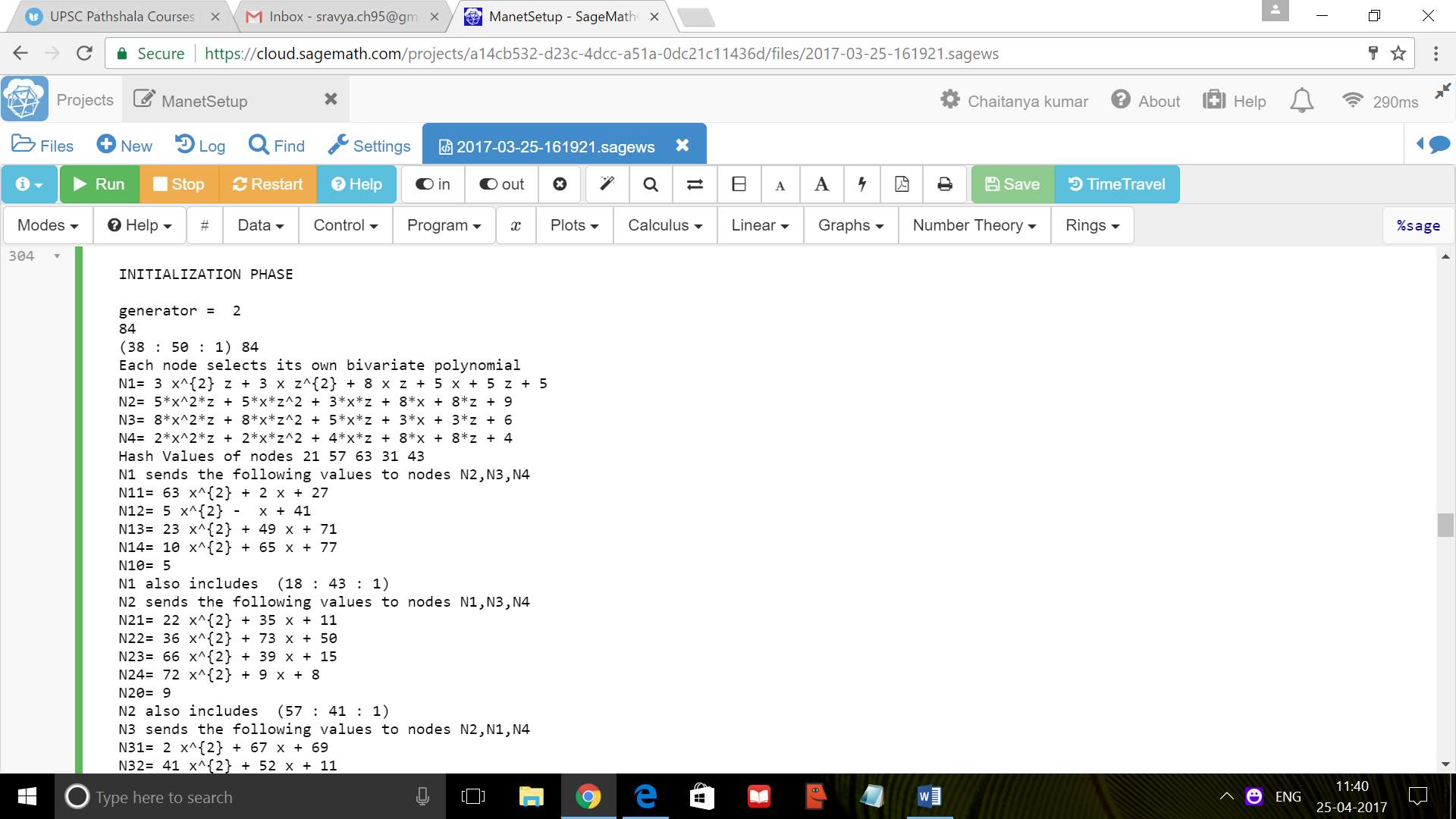
N1 = 3*x^2*z+3*z^2*x+8*x*z+5*z+5*x+5
N2 = 5*x^2*z+5*x*z^2+3*x*z+8*z+8*x+9
N3 = 8*x^2*z + 8*x*z^2+5*x*z+3*x+3*z+6
N4 = 2*x^2*z+2*x*z^2+4*x*z+8*z+8*x+4
#N5 = 3*x^2*z+3*z^2*x+8*x*z+5*z+5*x+5
print ‘Each node selects its own bivariate polynomial’
print ‘N1=’,latex(N1)
print ‘N2=’,N2
print ‘N3=’,N3
print ‘N4=’,N4
#print ‘N5=’,N5
#STEP_2 All the nodes exchanges messages secretly Using Hash function
# The following hash function is used
import hashlib
def hfun(id,k):
h = int(hashlib.sha224(str(id)).hexdigest(),16)
val = mod(h,k)
return val
#The hash values of the nodes are calculated as Follows
h_n1 = hfun(‘Node1’,k1)
h_n2 = hfun(‘Node2’,k1)
h_n3 = hfun(‘Node3’,k1)
h_n4 = hfun(‘Node4’,k1)
h_n5 = hfun(‘Node5’,k1)
h_sg = hfun(‘Node_1_2_3’,k1);
print ‘Hash Values of nodes’,h_n1,h_n2,h_n3,h_n4,h_n5
print ‘N1 sends the following values to nodes N2,N3,N4′
N11.<x>=PolynomialRing(F1,1,order=’lex’)
N12.<x>=PolynomialRing(F1,1,order=’lex’)
N13.<x>=PolynomialRing(F1,1,order=’lex’)
N14.<x>=PolynomialRing(F1,1,order=’lex’)
N11 = N1(x,h_n1)
N12 = N1(x,h_n2)
N13 = N1(x,h_n3)
N14 = N1(x,h_n4)
print ‘N11=’ ,latex(N11)
print ‘N12=’ ,latex(N12)
print ‘N13=’ ,latex(N13)
print ‘N14=’ ,latex(N14)
N10 = N1(0,0)
print ‘N10=’,N10
print ‘N1 also includes ‘,int(N1(0,0))*P
print ‘N2 sends the following values to nodes N1,N3,N4′
N21.<x>=PolynomialRing(F1,1,order=’lex’)
N22.<x>=PolynomialRing(F1,1,order=’lex’)
N23.<x>=PolynomialRing(F1,1,order=’lex’)
N24.<x>=PolynomialRing(F1,1,order=’lex’)
N21 = N2(x,h_n1)
N22 = N2(x,h_n2)
N23 = N2(x,h_n3)
N24 = N2(x,h_n4)
print ‘N21=’ ,latex(N21)
print ‘N22=’ ,latex(N22)
print ‘N23=’ ,latex(N23)
print ‘N24=’ ,latex(N24)
N20 = N2(0,0)
print ‘N20=’,N20
print ‘N2 also includes ‘,int(N2(0,0))*P
print ‘N3 sends the following values to nodes N2,N1,N4′
N31.<x>=PolynomialRing(F1,1,order=’lex’)
N32.<x>=PolynomialRing(F1,1,order=’lex’)
N33.<x>=PolynomialRing(F1,1,order=’lex’)
N34.<x>=PolynomialRing(F1,1,order=’lex’)
N31 = N3(x,h_n1)
N32 = N3(x,h_n2)
N33 = N3(x,h_n3)
N34 = N3(x,h_n4)
print ‘N31=’ ,latex(N31)
print ‘N32=’ ,latex(N32)
print ‘N33=’ ,latex(N33)
print ‘N34=’ ,latex(N34)
N30 = N3(0,0)
print ‘N30=’,N30
print ‘N3 also includes ‘,int(N3(0,0))*P
print ‘N4 sends the following values to nodes N2,N3,N1′
N41.<x>=PolynomialRing(F1,1,order=’lex’)
N42.<x>=PolynomialRing(F1,1,order=’lex’)
N43.<x>=PolynomialRing(F1,1,order=’lex’)
N44.<x>=PolynomialRing(F1,1,order=’lex’)
N41 = N4(x,h_n1)
N42 = N4(x,h_n2)
N43 = N4(x,h_n3)
N44 = N4(x,h_n4)
print ‘N41=’ ,latex(N41)
print ‘N42=’ ,latex(N42)
print ‘N43=’ ,latex(N43)
print ‘N44=’ ,latex(N44)
N40 = N4(0,0)
print ‘N40=’,N40
print ‘N4 also includes ‘,int(N4(0,0))*P
S1.<x>=PolynomialRing(F1,1,order=’lex’)
S1 = N11+N21+N31+N41
S2.<x>=PolynomialRing(F1,1,order=’lex’)
S2 = N12+N22+N32+N42
S3.<x>=PolynomialRing(F1,1,order=’lex’)
S3 = N13+N23+N33+N43
S4.<x>=PolynomialRing(F1,1,order=’lex’)
S4 = N14+N24+N34+N44
Q.<x,z>=PolynomialRing(F1,2,order=’lex’)
Q = N1+N2+N3+N4
print ‘The secret of MANET is ‘,Q,Q(0,0)
print ‘The secret polynomials of each node is’
print ‘At node N1=’,S1,’And the corresponding share is=’,S1(0)
print ‘At node N2=’,S2,’And the corresponding share is=’,S2(0)
print ‘At node N3=’,S3,’And the corresponding share is=’,S3(0)
print ‘At node N4=’,S4,’And the corresponding share is=’,S4(0)
print ‘verifiaction’
Q1 = Q(x,h_n1)
print ‘the verified polynomial is’ , Q1
Q2 = Q(x,h_n2)
print ‘the verified polynomial is’ , Q2
Q3 = Q(x,h_n3)
print ‘the verified polynomial is’ , Q3
Q4 = Q(x,h_n4)
print ‘the verified polynomial is’ , Q4
K = int(N1(0,0))*P +int(N2(0,0))*P +int(N3(0,0))*P+int(N4(0,0))*P
print ‘MANET public key is’,K
print ‘S1:’,S1,’;S2:’,S2,’;S3:’,S3
T15 = ((x-h_n2)*(x-h_n3)*(S1))/((h_n1-h_n3)*(h_n1-h_n2))
T25 = ((x-h_n1)*(x-h_n3)*(S2))/((h_n2-h_n1)*(h_n2-h_n3))
T45 = ((x-h_n1)*(x-h_n2)*(S3))/((h_n3-h_n1)*(h_n3-h_n2))
S5_3 = T15 + T25 + T45;
print ‘S5’,S5_3
print int(S5_3(0,0))
print ‘Addition of new node N5′
N5.<x,z>=PolynomialRing(F1,2,order=’lex’)
print ‘N5 Requests the following values to nodes N2,N1,N3′
N51.<x>=PolynomialRing(F1,1,order=’lex’)
N52.<x>=PolynomialRing(F1,1,order=’lex’)
N53.<x>=PolynomialRing(F1,1,order=’lex’)
N51 = S1(h_n5)
N52 = S2(h_n5)
N53 = S3(h_n5)
print ‘N51=’ ,latex(N51)
print ‘N52=’ ,latex(N52)
print ‘N53=’ ,latex(N53)
print ‘The new polynomial N5 is’
print ‘N51:’,N51,’;N52:’,N52,’;N53:’,N53
T65 = ((x-h_n3)*(x-h_n2)*(N51))/((h_n1-h_n3)*(h_n1-h_n2))
T75 = ((x-h_n1)*(x-h_n3)*(N52))/((h_n2-h_n1)*(h_n2-h_n3))
T55 = ((x-h_n1)*(x-h_n2)*(N53))/((h_n3-h_n1)*(h_n3-h_n2))
S5_4 = T65 + T75 + T55;
print ‘S55’,latex(S5_4)
print latex(Q(x,h_n5))
print ‘Share Verification ‘
print ‘Node 1 sends to node 2, polynomial’,N12,’and commitment’
c12 = int (3 * h_n2^2) * P + int( 16 * h_n2) * P + 10 * P
print c12
print ‘node2 verifies is as 5 * P + 82 * P + 41 * P’
cn12 = 5 * P + 82 * P + 41 * P
print cn12
print ‘Share Renewal Process’
N1_1.<x,z>=PolynomialRing(F1,2,order=’lex’)
N2_1.<x,z>=PolynomialRing(F1,2,order=’lex’)
N3_1.<x,z>=PolynomialRing(F1,2,order=’lex’)
N4_1.<x,z>=PolynomialRing(F1,2,order=’lex’)
N1_1 = x^2*z+z^2*x+5*x*z+2*z+2*x
N2_1 = 2*x^2*z+2*x*z^2+20*x*z+4*z+4*x
N3_1 = 3*x^2*z + 3*x*z^2+12*x*z+x+z
N4_1 = 4*x^2*z+4*x*z^2+8*x*z+3*z+3*x
N1_11.<x>=PolynomialRing(F1,1,order=’lex’)
N1_12.<x>=PolynomialRing(F1,1,order=’lex’)
N1_13.<x>=PolynomialRing(F1,1,order=’lex’)
N1_14.<x>=PolynomialRing(F1,1,order=’lex’)
N1_11 = N1_1(x,h_n1)
N1_12 = N1_1(x,h_n2)
N1_13 = N1_1(x,h_n3)
N1_14 = N1_1(x,h_n4)
print ‘N1_11=’ ,latex(N1_11)
print ‘N1_12=’ ,latex(N1_12)
print ‘N1_13=’ ,latex(N1_13)
print ‘N1_14=’ ,latex(N1_14)
print ‘N2 sends the following values to nodes N1,N3,N4′
N2_21.<x>=PolynomialRing(F1,1,order=’lex’)
N2_22.<x>=PolynomialRing(F1,1,order=’lex’)
N2_23.<x>=PolynomialRing(F1,1,order=’lex’)
N2_24.<x>=PolynomialRing(F1,1,order=’lex’)
N2_21 = N2_1(x,h_n1)
N2_22 = N2_1(x,h_n2)
N2_23 = N2_1(x,h_n3)
N2_24 = N2_1(x,h_n4)
print ‘N2_21=’ ,latex(N2_21)
print ‘N2_22=’ ,latex(N2_22)
print ‘N2_23=’ ,latex(N2_23)
print ‘N2_24=’ ,latex(N2_24)
print ‘N3 sends the following values to nodes N2,N1,N4′
N3_31.<x>=PolynomialRing(F1,1,order=’lex’)
N3_32.<x>=PolynomialRing(F1,1,order=’lex’)
N3_33.<x>=PolynomialRing(F1,1,order=’lex’)
N3_34.<x>=PolynomialRing(F1,1,order=’lex’)
N3_31 = N3_1(x,h_n1)
N3_32 = N3_1(x,h_n2)
N3_33 = N3_1(x,h_n3)
N3_34 = N3_1(x,h_n4)
print ‘N3_31=’ ,latex(N3_31)
print ‘N3_32=’ ,latex(N3_32)
print ‘N3_33=’ ,latex(N3_33)
print ‘N3_34=’ ,latex(N3_34)
print ‘N4 sends the following values to nodes N2,N3,N1′
N4_41.<x>=PolynomialRing(F1,1,order=’lex’)
N4_42.<x>=PolynomialRing(F1,1,order=’lex’)
N4_43.<x>=PolynomialRing(F1,1,order=’lex’)
N4_44.<x>=PolynomialRing(F1,1,order=’lex’)
N4_41 = N4_1(x,h_n1)
N4_42 = N4_1(x,h_n2)
N4_43 = N4_1(x,h_n3)
N4_44 = N4_1(x,h_n4)
print ‘N4_41=’ ,latex(N4_41)
print ‘N4_42=’ ,latex(N4_42)
print ‘N4_43=’ ,latex(N4_43)
print ‘N4_44=’ ,latex(N4_44)
S11.<x>=PolynomialRing(F1,1,order=’lex’)
print ‘ the new shares recieved at N1 is ‘
N111 = N1_11 + N2_21 + N3_31 + N4_41
S11 = S1 + N111
S22.<x>=PolynomialRing(F1,1,order=’lex’)
print ‘ the new shares recieved at N1 is ‘
N222 = N1_12 + N2_22 + N3_32 + N4_42
S22 = S2 + N222
S33.<x>=PolynomialRing(F1,1,order=’lex’)
print ‘ the new shares recieved at N1 is ‘
N333 = N1_13 + N2_23 + N3_33 + N4_43
S33 = S3 + N333
S44.<x>=PolynomialRing(F1,1,order=’lex’)
print ‘ the new shares recieved at N1 is ‘
N444 = N1_14 + N2_24 + N3_34 + N4_44
S44 = S4 + N444
print ‘ The new Polynomials of the nodes along with their share are ‘
print ‘N1 = ‘, S11 ,’ share = ‘, S11(0)
print ‘N2 = ‘, S22 ,’ share = ‘, S22(0)
print ‘N3 = ‘, S33 ,’ share = ‘, S33(0)
print ‘N4 = ‘, S44 ,’ share = ‘, S44(0)
Q1.<x,z>=PolynomialRing(F1,2,order=’lex’)
Q1 = Q + N1_1 + N2_1 + N3_1 + N4_1
print ‘The secret of MANET is ‘,Q1,Q1(0,0)
OUTPUT:
5 CONCLUSION
In this project, we proposed a new scheme of verifying a certificate in decentralized PKI based MANETS. In our scheme the nodes of the MANET holds a secret share and every node chooses its own public and private keys. The public key is associated with the node identity in the certificate. This certificate management is done using BLS Signature.
6 REFERENCES
[1] F. Anjum and P. Mouchtaris, Security for wireless ad hoc networks. Wiley-Blackwell, Mar. 2007.
[2] Vanesa Daza, Javier Herranz, Paz Morillo, Carla Rfols, Cryptographic techniques for mobile ad-hoc networks, Computer Networks, Volume 51, Issue 18, 19 December 2007, Pages 4938-4950
[3] Y.-C. Hu, A. Perrig, and D. B. Johnson. Ariadne: A secure ondemand routing protocol for ad hoc networks. In Proceedings of the Eighth ACM International Conference on Mobile Computing and Networking (Mobicom 2002), September 2002.
[4] Y.-C. Hu, A. Perrig, and D. B. Johnson. Packet leashes: A defense against wormhole attacks in wireless networks. In Proceedings of IEEE Infocom 2003, April 2003.
[5] S. Kent and T. Polk. Public-key infrastructure (x.509) (pkix) charter. http://www.ietf.org/html.charters/pkix-charter.html.
[6] L. Zhou, Z.J. Haas, Securing ad hoc networks, IEEE Network 13 (6) (1999) 2430.
[7] G.R. Blakley, Safeguarding cryptographic keys, in: Proceed- ings of the National Computer Conference, American Federation of Information, Processing Societies Proceedings, vol. 48, 1979, pp. 313317.
[8] A. Shamir, How to share a secret, Communications of the ACM 22 (1979) 612613.
[9] Seung Yi and Robin Kravetso. Moca : Mobile certificate authority for wireless ad hoc networks. In The second anunual PKI research workshop (PKI 03), Gaithersburg, 2003.
[10] Dan Boneh, Ben Lynn, and Hovav Shacham (2004). ”Short Signatures from the Weil Pairing”. Journal of Cryptology. 17: 297319.
[11] Djenouri, Djamel, L. Khelladi, and N. Badache. ”A survey of security issues in mobile ad hoc networks.” IEEE communications surveys 7.4 (2005): 2-28.
[12] Stallings, William (1990-05-03). Cryptography and Network Security: Principles and Practice. Prentice Hall. p. 165. ISBN 9780138690175.
[13] H. Luo, J. Kong, P. Zerfos, S. Lu, L. Zhang, URSA: ubiquitous and robust access control for mobile ad hoc networks, IEEE/ACM Transactions on Networking 12 (6) (2004) 10491063.
[14] M. Narasimha, G. Tsudik, J.H. Yi, On the utility of distributed cryptography in P2P and MANETs: the case of membership control, in: Proceedings of ICNP03, 2003, pp. 336345.
[15] S. Jarecki, N. Saxena, J.H. Yi, An attack on the proactive RSA signature scheme in the URSA ad hoc network access control protocol, in: Proceedings of the SASN04, 2004, pp. 19.
[16] C. Blundo, A. De Santis, A. Herzberg, S. Kutten, U. Vaccaro, M. Yung, Perfectly-secure key distribution for dynamic conferences, in: Proceedings of Crypto92, LNCS, vol. 740, Springer-Verlag, 1993, pp. 471486.
[17] J.Anzai,N.Matsuzaki,T.Matsumoto,Aquickgroupkeydistribution scheme with entity revocation, in: Proceedings of Asiacrypt99, LNCS, vol. 1716, Springer-Verlag, 1999, pp. 333347.
[18] V. Daza, J. Herranz, G. Sez, Constructing general dynamic group key distribution schemes with decentralized user join, in: ProceedingsofACISP03,LNCS,vol.2727,Springer-Verlag,2003,pp.464475.
[19] N. Saxena, G. Tsudik, J.H. Yi, Efficient node admission for shortlived mobile ad hoc networks, in: Proceedings of ICNP05, 2005, pp. 269278.
[20] Boneh, Dan, and Matt Franklin. ”Identity-based encryption from the Weil pairing.” Annual International Cryptology Conference.
Cite This Work
To export a reference to this article please select a referencing stye below:
Related Services
View allRelated Content
All TagsContent relating to: "Computer Science"
Computer science is the study of computer systems, computing technologies, data, data structures and algorithms. Computer science provides essential skills and knowledge for a wide range of computing and computer-related professions.
Related Articles
DMCA / Removal Request
If you are the original writer of this dissertation and no longer wish to have your work published on the UKDiss.com website then please:




