Pose Scoring and Minimization using Convolutional Neural Networks

Abstract

Computational technologies optimize the drug discovery process as they reduce the requirement of experimental assays and permit the analysis of novel chemical structures. Structure-based drug design in particular utilises computational scoring functions for ranking ligand poses and predicting binding affinity. Docking algorithms are used to efficiently traverse the ligand pose search space to arrive at the binding pose. Essentially they are designed to find the orientation with the best score according to the scoring function. With the ever increasing availability of ligand-protein binding and structural data, Deep Learning algorithms can be adopted to make an efficient scoring functions. In this work we explored the usage of a Convolutional Neural Network (CNN) to predict the distance of an arbitrary ligand pose from the true binding pose of a protein-ligand complex. Subsequently we paired the trained model as a scoring function with a monte carlo based search algorithm to evaluate its performance while docking.

Contents

Abbreviations vi

1 Introductiom 1

1.1 Scoring and Docking 1

1.2 Deep Learning & CNNs 2

1.3 Thesis Scope 3

2 Model Training 4

2.1 Data and Representation 4

2.2 Training 5

2.3 Minimization 6

2.4 Iterative Training 7

3 Docking 10

3.1 Algorithm 10

3.2 Results 11

4 Conclusion 12

Bibliography 13

List of Figures

2.1 Model Architecture

2.2 1st Correlation Results

2.3 1st Minimization Results

2.4 2nd Iteration Results

2.5 3rd Iteration Results

3.1 Docking Results

Abbreviations

BFGS	Broyden Fletcher Goldfarb Shanno
CADD	Computer Aided Drug Design
CNN	Convolutional Neural Networks
PDB	Protein Data Bank
RMSD	Root Mean Square Distance
SBDD	Structure Based Drug Design

Chapter 1: Introduction

Computational techniques in drug discovery have the potential to reduce the time and resource requirements for new molecule design. Computer-Aided Drug Design(CADD)is used for high throughput screening, molecular dynamic simulations as well as molecular property optimization[1]. Structure based drug design (SBDD) specifically uses the 3 dimensional structural information of the receptor to design and optimize chemical structures. It has the capability to improve the quality of lead molecules at lower costs[2], however it relies heavily on CADD methods and tools. Thus, it is of vital importance to continue developing better algorithms and resources to support SBDD and as an extension to support drug discovery.

1.1 Scoring and Docking

SBDD is dependant on an efficient scoring function that can be used to discriminate between binding ligands(Actives)and non-binding ligands(Decoys)[3]. Such a function can be used in high throughput virtual screening to find potential candidate ligand from large molecular libraries for further analysis. Furthermore they should also be able to effectively rank different orientations of the ligand in terms of binding affinity.

Scoring functions inspired by physical interactions are either knowledge-based models[4–8] or empirically parameterized[9–15] to provide a good fit to the data. Scoring functions that use machine learning[11, 16–26] are required to learn both, molecular structure as well as model parameters from the data. These models can capture binding features that are hard to model explicitly. This gives such models a great advantage but also makes it liable to over-fitting[27, 28].

Docking is an important part of the drug discovery and design process as it tries to predict the ideal binding pose of drug molecule with a target receptor through pose scoring and optimization[29]. Several docking algorithms follow the approach of combining the optimization algorithm with a scoring function. These methods use an efficient search algorithm that traverses the ligand orientation space to find the optimal poses according to the scoring functions. Therefore the scoring function is used to guide pose sampling and ranking. For example, the scoring is used to influence monte carlo sampling in Autodock Vina[9].

1.2 Deep Learning & CNNs

Neural networks[30] are a form of supervised machine learning algorithms that are inspired by the neural structure of the human brain. These neural networks consist of multiple layers of interconnected neurons or units. Each neuron unit perform a nonlinear function to derive a relationship from all of it's inputs. A basic neural network consists of an input layer, a hidden layer and an output layer. Deep learning[31] architectures are neural networks that contain multiple hidden layers and are capable of learning complex relationships. The network architecture needs to be tuned to fit the data well and avoid over-fitting. Scoring functions based on neural networks[16, 17, 21–24, 26] have shown competitive performance as compared to empirical scoring functions in virtual screening and pose ranking tasks.

Convolutional Neural Networks (CNN)[31] are specially designed neural networks that can be used with images effectively. They have several use cases in computer vision such as image recognition, segmentation, classification etc. These networks are typically composed of convolutional kernels that can detect specific features in images like horizontal or vertical edges. The layer hierarchy in a CNN detect different levels of features in an image. For instance, the first layer may only detect lines and corners in an image while the final layer may recognise complex shapes like different breeds of cats or dogs. CNNs are the current state of the art methods of image recognition as shown by the winning entry of Microsoft ResNet to the ImageNet Large Scale Visual Recognition Challenge of 2015[32].

1.3 Thesis Scope

The abundant availability of three dimensional structure for these proteins and ligands makes docking a natural extension of a computer vision problem. Computer vision algorithms based on Convolutional Neural Networks (CNN) have been known to perform well in image recognition tasks and thus should be able to perform well as a scoring function for protein ligand binding.

A 3-dimensional grid representation of the molecules enables spatial relationship to be extracted by a CNN model. In previous works, it has been shown that CNNs using this representation can effectively learn to discriminate between binding and non binding poses[16] or predict binding affinity[17]. The CNN score and gradients can also be decomposed into individual atomistic contributions[33]. Therefore, the learnt gradients from the network can be propogated to individual atoms and thus can be used to optimize poses with respect to the atom positions.

The current work explores this methodology by building a CNN scoring function that predicts the RMSD of a particular pose from the crystal pose and uses it's learnt gradients for ligand pose optimization. It employs an iterative training[33, 34] process to ensure sensitivity to bad poses and steric hindrance. This model is subsequently paired with the monte carlo sampling and local optimization algorithm design in Autodock Vina. This is easily done using the simple gnina tool[16]. The model shows a potential to improve the docking performance as compared to the Vina scoring function. A drawback of the algorithm, however, is the high time requirement which is caused due to multiple forward and backward passes through the model during local optimization.

Chapter 2: Model Training

2.1 Data and Representation

The Protein Data Bank (PDB)[35] contains 3D structural information and images of several proteins and protein-ligand complexes. This structural information enables the formation of a 3D voxelized representation of the molecules. The PDBbind dataset[36, 37] provides a comprehensive library of binding affinity for the protein-ligand complexes that have been deposited in the PDB database. The experiments are done on the PDBbind 2016 dataset. PDBbind 2016 also contains a subset of high quality complexes of 3805 complexes known as the refined set. We worked with this refined set for our purpose.

The molecules are represented in the form of atomic densities on a 3D grid with an extra 4th channel dimension representing the type of atom. We use the Smina[11] atom types for this purpose. The atomic density was generated using Gnina on a 3-D grid. The atomic density is represented on a grid g(d,r) according to the following formula:

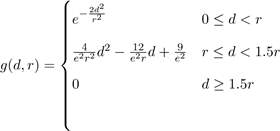(2.1)

4

Where d is the distance to the grid point and r is the Van der Waals radius of the atom. We used a cubic grid with an edge size of 23.5 Angstrom. The resolution per pixel used was 0.5 Angstrom.

2.2 Training

The refined set was split into 3 parts based on protein similarity for 3-fold cross validation. The ligands were docked and 20 poses were generated for each complex using the vina scoring function and Smina. The RMSD between the created poses and the crystal pose was found using the obrms module provided by openbabel[38].

Figure 2.1 shows the CNN model architecture used. We used the custom Gnina Caffe version for model training. The model was trained using Nesterov Accelerated Gradient Descent [39] with a base learning rate of = 0.01, momentum = 0.9 and weight decay = 0.001. The model was trained to minimize the Euclidean loss between the predicted and true RMSD. We used a batch size of 50 samples and the MolGridDataLayer was used to arbitrarily rotate and translate structures while training to ensure equivariance. Figure 2.2 shows the Spearman Correlation between the predicted and true RMSD and the RMSE of the predictions.

Figure 2.2: Root Mean Square Error (RMSE) and Correlation between predicted and true RMSD

2.3 Minimization

The gradients developed from training can be propogated to each individual atom [33]. These gradients can be used for optimization of the ligand pose. The Broyden Fletcher Goldfarb Shanno algorithm (BFGS)[40] algorithm is a multi-variate technique for optimization that utilises the gradient to reach the local minima. BFGS is used to minimize the ligand orientation according to the score provided by CNN model. The partial derivative of the scoring function f with respect to atomic coordinates a is obtained easily via chain rule(equation 2.2) and is treated as forces applied to each atom.

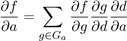(2.2)

Figure 2.3: Change in RMSD after local optimization of poses using 1st iteration model

The first derivation of the chain rule is obtained through backpropagation and other parts calculated easily using the density formula(equation 2.1). As a result the optimization algorithm requires multiple forward and backward passes through the CNN for minimization.

The poses initially generated for the training and test dataset were sent for optimization using the BFGS algorithm. Figure 2.3 shows the change in rmsd as a result of optimizing the ligand orientations using BFGS. For most of the poses a change for the worse occured, this was an expected result[33] as the models had not been sensitized to steric hindrance and other extremely bad poses as of yet. This is because the dataset contained only possibles poses with high chance of good binding affinity and a lack of any steric hindrance and density overlap.

2.4 Iterative Training

In order to sensitize the model to bad poses and improve the performance of optimization a process of iterative training was done. In this strategy the generated poses from minimization were added to the original dataset for another round of training. The model was trained again for the 2nd iteration. This was then used again to minimize poses in the original dataset. We can see from Fig 2.4 that the correlation improve with the incorporation of these bad poses indicating a signal of improving performance. This improvement is also reflected in the minimization results with the distribution being less skewed as compared to before. An extended dataset was created with the incorporation of these minimized poses for a third round of training and optimization. Furthermore stratified sampling was done over a range of RMSD values (0-12) with bin sizes of 2 to generate batches of training and test. This was done in order to expose the model to equal amount of samples through the entire range of RMSD values. The results of the third iteration (Fig 2.5) show a very high spearman correlation between the predicted and experimental values of the test set indicating a well trained model. This is also realised from the results of minimization where the distribution is slightly left skewed thereby showing an improvement in majority of the poses.

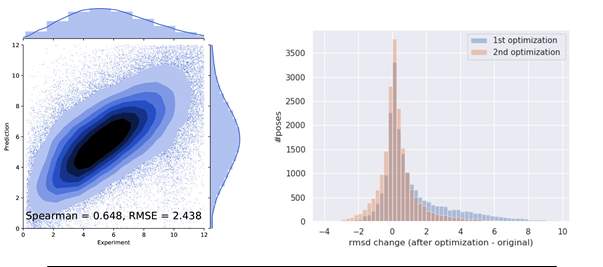
Figure 2.4: Results after 2nd Iteration training(left) and minimization(right)

Figure 2.5: Results after 3rd Iteration training(left) and minimization(right)

However, the strong centering at 0 in the minimization results indicate that the algorithm is getting stuck at local minima during optimization. This emphasizes the need of a better docking algorithm like a monte carlo search that is more robust to local minima.

Chapter 3: Docking

3.1 Algorithm

The CNN scoring function is coupled with a monte carlo sampling and local optimization method to form the docking algorithm. This method has been used previously by autodock vina. The algorithm proceeds by carrying out a number of steps to reach the global minima. Each step is performed, first by monte carlo sampling of the ligand orientations on it's degrees of freedom, followed by a local optimization of the produced sample by utilising BFGS. The location of each new sample produced is dependant on the location of the previous sample. The final sample is accepted if it satisfies the Metropolis criterion[41]. According to the criterion, a pose that is worse than the previous pose can only be accepted with some probability that is dependant on the difference between the two poses and the temperature of the system. If the generated pose is a better pose then it will always be accepted by the criterion.

We employed this algorithm easily using the gnina tool. The --cnn scoring argument specifies the usage of the CNN model, while the --cnn model and --cnn weights arguments are used to pass the .model file and .caffemodel file respectively. To evaluate, we compared the performance of the CNN model to that of the Vina scoring function. For this Monte Carlo chains of different lengths were performed for both the models using their respective scoring function for the Metropolis criterion. The chain length can be controlled using the --num mc steps argument. These chains were run on the default exhaustiveness parameter value as defined by gnina. The exhaustiveness parameter controls the amount of stochastic sampling while docking.

3.2 Results

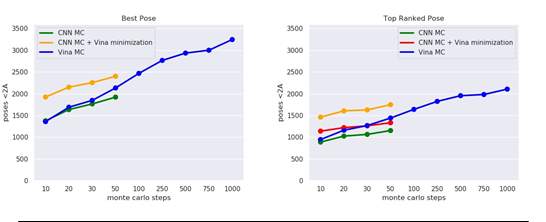
Figure 3.1: Number of Best Poses(left) and Top Ranked Poses(right) below 2 Angstrom from crystal binding pose

For comparison, we carried out monte carlo chains of different lengths using both the scoring functions across the dataset. These are referred to as CNN MC and Vina MC for the CNN model and Vina function respectively. Figure 3.1 illustrates the docking results in terms of the Top ranked poses and Best poses that were sampled. In addition, we also did a final local optimization of the poses generated by the CNN using the physically inspired Vina scoring function(CNN MC + Vina Minimization in fig). The figures show the number of complexes, out of 3594, where good poses were successfully sampled(left) and ranked correctly(right) by the scoring function. For the poses from CNN MC with final Vina local optimization, we ranked the poses using both the CNN model(CNN MC + Vina Minimization) as well as the Vina scoring function(CNN MC + Vina minimization & ranking).

The figures clearly indicate that performing Monte Carlo search using the CNN model and following it up by Vina local optimization and ranking would be the best form of docking algorithm. However, there is a high time requirement in carrying out a Monte Carlo and local optimization step search using the CNN model. This is due to the multiple forward and backward passes that are done through the model for local optimization.

Chapter 4: Conclusion

This thesis explored the usage of a Convolutional Neural Network(CNN) as a scoring function based on the Root Mean Square Distance(RMSD) of an arbitrary ligand orientation to the binding orientation. The CNN model was trained to a high spearman correlation with the true values after three rounds of iterative training. This result proves that the RMSD is a learnable value and can be learnt with a high correlation.

The CNN model proves to be useful while docking, especially if it is used to guide the Monte Carlo search. The results indicate a strong signal in using it and topping it off with a local minimization using the Vina scoring function. There is, however, a large time requirement in performing such searches thereby providing diminishing returns with increasing chain lengths. These results also show a potential of improving Vina ranking performance by using the CNN scoring function in tandem to refine the ranking results. Further work needs to be done to form an efficient consensus scoring function that takes advantage of both these models.

Bibliography

[1] G. Sliwoski, S. Kothiwale, J. Meiler, and E. W. Lowe, "Computational methods in drug discovery," Pharmacological reviews, vol. 66, no. 1, pp. 334–395, 2014.

[2] M. Aarthy, U. Panwar, C. Selvaraj, and S. K. Singh, "Advantages of structure-based drug design approaches in neurological disorders," Current neuropharmacology, vol. 15, no. 8, pp. 1136–1155, 2017.

[3] E. Lionta, G. Spyrou, D. K Vassilatis, and Z. Cournia, "Structure-based virtual screening for drug discovery: Principles, applications and recent advances," Current topics in medicinal chemistry, vol. 14, no. 16, pp. 1923–1938, 2014.

[4] S.-Y. Huang and X. Zou, "Mean-force scoring functions for protein–ligand binding," in Annual Reports in Computational Chemistry, vol. 6, Elsevier, 2010, pp. 280–296.

[5] I. Muegge and Y. C. Martin, "A general and fast scoring function for protein- ligand interactions: A simplified potential approach," Journal of medicinal chemistry, vol. 42, no. 5, pp. 791–804, 1999.

[6] H. Gohlke, M. Hendlich, and G. Klebe, "Knowledge-based scoring function to predict protein-ligand interactions," Journal of molecular biology, vol. 295, no. 2, pp. 337–356, 2000.

[7] H. Zhou and J. Skolnick, "Goap: A generalized orientation-dependent, all-atom statistical potential for protein structure prediction," Biophysical journal, vol. 101, no. 8, pp. 2043– 2052, 2011.

[8] W. T. Mooij and M. L. Verdonk, "General and targeted statistical potentials for protein– ligand interactions," Proteins: Structure, Function, and Bioinformatics, vol. 61, no. 2, pp. 272–287, 2005.

[9] O. Trott and A. J. Olson, "Autodock vina: Improving the speed and accuracy of docking with a new scoring function, efficient optimization, and multithreading," Journal of computational chemistry, vol. 31, no. 2, pp. 455–461, 2010.

[10] R. Wang, L. Lai, and S. Wang, "Further development and validation of empirical scoring functions for structure-based binding affinity prediction," Journal of computer-aided molecular design, vol. 16, no. 1, pp. 11–26, 2002.

[11] D. R. Koes, M. P. Baumgartner, and C. J. Camacho, "Lessons learned in empirical scoring with smina from the csar 2011 benchmarking exercise," Journal of chemical information and modeling, vol. 53, no. 8, pp. 1893–1904, 2013.

[12] H.-J. B¨ohm, "The development of a simple empirical scoring function to estimate the binding constant for a protein-ligand complex of known three-dimensional structure," Journal of computer-aided molecular design, vol. 8, no. 3, pp. 243–256, 1994.

[13] R. A. Friesner, J. L. Banks, R. B. Murphy, T. A. Halgren, J. J. Klicic, D. T. Mainz, M. P. Repasky, E. H. Knoll, M. Shelley, J. K. Perry, et al., "Glide: A new approach for rapid, accurate docking and scoring. 1. method and assessment of docking accuracy," Journal of medicinal chemistry, vol. 47, no. 7, pp. 1739–1749, 2004.

[14] O. Korb, T. Stutzle, and T. E. Exner, "Empirical scoring functions for advanced proteinligand docking with plants," Journal of chemical information and modeling, vol. 49, no. 1, pp. 84–96, 2009.

[15] M. D. Eldridge, C. W. Murray, T. R. Auton, G. V. Paolini, and R. P. Mee, "Empirical scoring functions: I. the development of a fast empirical scoring function to estimate the binding affinity of ligands in receptor complexes," Journal of computer-aided molecular design, vol. 11, no. 5, pp. 425–445, 1997.

[16] M. Ragoza, J. Hochuli, E. Idrobo, J. Sunseri, and D. R. Koes, "Protein–ligand scoring with convolutional neural networks," Journal of chemical information and modeling, vol. 57, no. 4, pp. 942–957, 2017.

[17] J. Jim´enez, M. Skalic, G. Martinez-Rosell, and G. De Fabritiis, "K deep: Protein–ligand absolute binding affinity prediction via 3d-convolutional neural networks," Journal of chemical information and modeling, vol. 58, no. 2, pp. 287–296, 2018.

[18] L. Schietgat, T. Fannes, and J. Ramon, "Predicting protein function and protein-ligand interaction with the 3d neighborhood kernel," in International Conference on Discovery Science, Springer, 2015, pp. 221–235.

[19] P. J. Ballester and J. B. Mitchell, "A machine learning approach to predicting protein– ligand binding affinity with applications to molecular docking," Bioinformatics, vol. 26, no. 9, pp. 1169–1175, 2010.

[20] D. Zilian and C. A. Sotriffer, "Sfcscore rf: A random forest-based scoring function for improved affinity prediction of protein–ligand complexes," Journal of chemical information and modeling, vol. 53, no. 8, pp. 1923–1933, 2013.

[21] J. D. Durrant and J. A. McCammon, "Nnscore 2.0: A neural-network receptor–ligand scoring function," Journal of chemical information and modeling, vol. 51, no. 11, pp. 2897– 2903, 2011.

[22] I. Wallach, M. Dzamba, and A. Heifets, "Atomnet: A deep convolutional neural network for bioactivity prediction in structure-based drug discovery," arXiv preprint arXiv:1510.02855, 2015.

[23] A. Gonczarek, J. M. Tomczak, S. Zareba, J. Kaczmar, P. Dabrowski, and M. J. Walczak, "Learning deep architectures for interaction prediction in structure-based virtual screening," arXiv preprint arXiv:1610.07187, 2016.

[24] V. Chupakhin, G. Marcou, I. Baskin, A. Varnek, and D. Rognan, "Predicting ligand binding modes from neural networks trained on protein–ligand interaction fingerprints," Journal of chemical information and modeling, vol. 53, no. 4, pp. 763–772, 2013.

[25] H. M. Ashtawy and N. R. Mahapatra, "Machine-learning scoring functions for identifying native poses of ligands docked to known and novel proteins," BMC bioinformatics, vol. 16, no. 6, S3, 2015.

[26] W. Torng and R. B. Altman, "Graph convolutional neural networks for predicting drugtarget interactions," Journal of Chemical Information and Modeling, vol. 59, no. 10, pp. 4131–4149, 2019.

[27] J. Gabel, J. Desaphy, and D. Rognan, "Beware of machine learning-based scoring functions on the danger of developing black boxes," Journal of chemical information and modeling, vol. 54, no. 10, pp. 2807–2815, 2014.

[28] C. Kramer and P. Gedeck, "Leave-cluster-out cross-validation is appropriate for scoring functions derived from diverse protein data sets," Journal of chemical information and modeling, vol. 50, no. 11, pp. 1961–1969, 2010.

[29] X.-Y. Meng, H.-X. Zhang, M. Mezei, and M. Cui, "Molecular docking: A powerful approach for structure-based drug discovery," Current computer-aided drug design, vol. 7, no. 2, pp. 146–157, 2011.

[30] R. Rojas, Neural networks: a systematic introduction. Springer Science & Business Media, 2013.

[31] Y. LeCun, Y. Bengio, and G. Hinton, "Deep learning," nature, vol. 521, no. 7553, pp. 436–444, 2015.

[32] K. He, X. Zhang, S. Ren, and J. Sun, "Deep residual learning for image recognition," in Proceedings of the IEEE conference on computer vision and pattern recognition, 2016, pp. 770–778.

[33] M. Ragoza, L. Turner, and D. R. Koes, "Ligand pose optimization with atomic grid-based convolutional neural networks," arXiv preprint arXiv:1710.07400, 2017.

[34] J. Hochuli, A. Helbling, T. Skaist, M. Ragoza, and D. R. Koes, "Visualizing convolutional neural network protein-ligand scoring," Journal of Molecular Graphics and Modelling, vol. 84, pp. 96–108, 2018.

[35] H. M. Berman, P. E. Bourne, J. Westbrook, and C. Zardecki, "The protein data bank," in Protein Structure, CRC Press, 2003, pp. 394–410.

[36] R. Wang, X. Fang, Y. Lu, and S. Wang, "The pdbbind database: Collection of binding affinities for protein- ligand complexes with known three-dimensional structures," Journal of medicinal chemistry, vol. 47, no. 12, pp. 2977–2980, 2004.

[37] R. Wang, X. Fang, Y. Lu, C.-Y. Yang, and S. Wang, "The pdbbind database: Methodologies and updates," Journal of medicinal chemistry, vol. 48, no. 12, pp. 4111–4119, 2005.

[38] N. M. O'Boyle, M. Banck, C. A. James, C. Morley, T. Vandermeersch, and G. R. Hutchison, "Open babel: An open chemical toolbox," Journal of cheminformatics, vol. 3, no. 1, p. 33, 2011.

[39] T. Dozat, "Incorporating nesterov momentum into adam," 2016.

[40] J. Nocedal and S. Wright, Numerical optimization. Springer Science & Business Media, 2006.

[41] S. Chib and E. Greenberg, "Understanding the metropolis-hastings algorithm," The american statistician, vol. 49, no. 4, pp. 327–335, 1995.