Synopsis Particle Swarm Optimization (PSO) is a robust and population based optimization algorithm. To solve the optimization problem, this algorithm applies the social intelligence of swarms. Dr. James Kennedy and Dr. Russel Eberhart were proposed the first version of this algorithm in 1995. In this version, a set of potential solutions (called as particles), are dispersed at various points in the solution space. Each point has some objective function value, and thus has fitness, for its current location. Each particle’s movement is influenced by the following two factors: (1) The best fitness achieved by the particle so far (BFS) and (2) The best fitness achieved by any particle in the neighbourhood (BFN). PSO is based on the social behaviour of bird flocking and fish schooling. Each swarm in bird flocking and fish schooling, update its position by following collective best position of the group and its own position. In the recent years PSO has been applied in various researches and real world problems e.g. global optimization, image processing, training of artificial neural network etc. In population based optimization algorithms, there is an avid necessity of a new kind of algorithm which improves the performance of the existing algorithm. Parameter tuning approach has an important role in improving the performance of the Particle Swarm Optimization (PSO) algorithm. A number of PSO variants based on parameter tuning approach, such as PSO-Time Varying Inertia Weight (PSO-TVIW), PSO-Random Inertia Weight (PSO-RANDIW), and PSO-Time Varying Acceleration Coefficient (PSO-TVAC) etc. have been proposed during the past few years. That motivates to develop a new optimization algorithm which applies a novel parameter tuning strategy which gives better results rather than the well-established state-of-the-art algorithms. In this thesis a modified version of PSO-TVAC has been proposed that applies a new parameter tuning technique. In the proposed work, velocity vector, acceleration and time varying inertia weight of PSO- TVAC decreases in a non-linear fashion in each generation (iteration). Performance of the modified PSO-TVAC namely PSO-MTVAC has been checked over 24 benchmark functions taken from COCO framework. It is found that the proposed algorithm shows its superiority over other state-of-the-art algorithms. Chapter 1 Introduction

1.1  Introduction

Optimization problems arise in various disciplines such as engineering  designs, agricultural sciences, manufacturing systems, economics, physical sciences, pattern recognition etc. and can be defined as the act of obtaining the best result under the given circumstances. It can also be defined as the process of finding the conditions that give the minimum or maximum value of a function, where the function represents the effort required or the desired benefit. Optimization is the process used to find best solution that addresses a certain problem. An optimization is a technique of finding the optimal solution from all feasible solutions. An important part of the optimization problem is the function is to be optimized. This function is called the objective function, also known as fitness function. The objective function, its search space and its constraints are all parts of the optimization problem. In the past few decades, number of global optimization algorithms has been developed that are based on the nature inspired analogy. Simulated annealing, evolutionary algorithms including genetic algorithms, and neural network methods represent a new class of mathematical programming techniques that have come into prominence during the last decade. These are mostly population based meta-heuristics and arealso called general purpose algorithms because of their applicability to a wide range of problems. Swarm Intelligence (SI) is an innovative distributed intelligent paradigm for solving optimization problems that originally took its inspiration from the biological examples by swarming, flocking and herding phenomena in vertebrates. Particle Swarm Optimization

(PSO) incorporates swarming behaviors observed in flocks of birds, schools of fish, or swarms of bees, and even human social behavior, from which the idea has emerged [1, 2]. PSO is a population-based optimization tool, which could be implemented and applied easily to solve various function optimization problems.PSOis based on the idea that individuals are able to evolve by exchanging information with their neighbours through social interaction. This is known as cognitive ability.Similar to Genetic Algorithms, PSO also starts with a population of random solutions and searches for optima by uploading generations. But PSO does not use evolutionary operators such as crossover and mutation as in GA. Three features impact on the evolution of the individual: Inertia (velocities cannot be changed abruptly), the individual itself (the individual could go back to the best solution found so far) and social influences (the individual could imitate the best solution found in its neighbour). As an algorithm, the main strength of PSO is its fast convergence, which compares favorably with many global optimization algorithms like Genetic Algorithms (GA) [3]simulated Annealing (SA) [4, 5] and other global optimization algorithms. For applying PSO successfully, one of the key issues is to map the problem solution into the PSO particle, which directly affects its feasibility and performance. There are many optimization techniques are proposed till now as mentioned above. But still it is required to establish a new optimization technique that should be able to work against the newly generated optimization problems. In population based optimization algorithms, there is an avid necessity of new kind of algorithm which improves the performance of the existing algorithm. In the proposed work, a new parameter  tuning strategy is used for PSO algorithm. The angle between the current position and its global best position is considered, and it is minimized in each iteration. The parameters of the PSO algorithm are varying form its maximum value to its minimum value in each iteration. Parameter tuning approach has an important role in improving the performance of the PSO algorithm. A number of PSO variants basedon parameter tuning approach, such as PSO-Time Varying Inertia Weight (PSO-TVIW) [6], PSO-Random Inertia Weight (PSO-RANDIW) [7], PSO-Time Varying Acceleration Coefficient (PSO-TVAC) [8] etc. have been proposed in past years. This motivates to develop a new type of parameter automation strategy which gives better performance than the previous algorithms.

1.2  Motivation

In population based optimization algorithm, there is an avid necessity of improving the performance of existing algorithm. In the past few years there are many variants of PSO have been proposed. Most of the variants are the result of parameter tuning. Few of them are PSO-TVIW, PSO-RANDIW and PSO-TVAC. In spite of their popularity, there are some drawbacks which are as follows:

• Thesealgorithms cannot work out the problems of scattering and optimization.
• They easily suffer from the practical optimism, which causes the less exact at the regulation of its speed and the direction.
• These algorithms have a problem-dependent performance. This dependency is usually caused by the wayparameters are set, i.e. assigning different parameter settings to thesealgorithms will result in high performance variance. So proper tuning of parameters is required to improve the performance of algorithm.
• They cannot work out the problems of non-coordinate systems, such as solution to the energy field and the moving rules of the particles in the energy filled.

1.3  Objective

The prime objective of the proposed work is to develop a modified time varying acceleration coefficient based PSO to solve unimodal and multimodal optimization problems. For that, the parameters of the PSO-TVAC have been tuned enoughto fulfil the following requirements:

• ImprovementinconvergenceRate:-This newly developed algorithm must be fast as compared to other available optimization algorithms. It means that it should be able to capture optimal solution in minimum number of generations.
• EscapefromLocalOptima:-Must be able to escape from local optima. This can be done by proper tuning of random parameters.
• Able to capture diversesolutions:-This can also be done by proper tuning of random parameters.

1.4  Structure of the Thesis

The whole thesis is organised into four sections which are as follows.

• Chapter 2, provides the literature survey on optimization algorithms with its variants and related work on parameter tuning techniques.
• Chapter 3, a modified version of Particle Swarm Optimization-Time Varying Acceleration Coefficient (PSO-TVAC) named as “Particle Swarm Optimization- Modified Time Varying Acceleration Coefficient (PSO-MTVAC)” is implemented.
• Chapter 4 discuses about experimental setup for benchmark testing of the proposed algorithm with experimental results.
• Chapter 5, conclusion and future direction for research is discussed.

Chapter2

Literature Survey and Related work

In mathematics and computer science, term optimization refers to the study of problems in which one seeks to minimize or maximize an objective function by systematically choosing the values of real or integer variables within an allowed set. Thus an optimization problem is the problem of finding the best solution from all feasible solutions. These optimization problems are very important because these are designed to either earn profit or to minimize the loss incurred. Due to their wide applicability in business, engineering and other areas, a number of algorithms have been proposed in literature to solve these problems to get optimal solutions in minimum possible time [1, 2]. Primary optimization algorithms were highly mathematical in nature. These algorithms use the value of the gradient at different points to target optimal solutions in a given problem. Different algorithm use different methods to calculate the value of gradients at different points. Since calculating the value of gradient at each point is a costly affair so these types of algorithm are not suitable for combinatorial problems. To overcome the limitation of gradient based approaches, Derivative free methods have been proposed. Some derivative free algorithms like Interpolation, Pattern search and Hooke-Jeeves direct methods evaluate the value of fitness function at many points and use these evaluations to target the value of optimal solution. However many times these algorithms trap in local optimum so other methods were sought. Finally to remove the limitation of these algorithms, heuristic algorithms were proposed. These algorithms evaluate the value of fitness function on some random points to target global optimal solutions. Many randomized algorithms such as evolutionary programming, evolutionary strategy, genetic algorithm, particle swarm optimization and genetic programming have already gained wide acceptance in solving such optimization problems. Since in these thesis variants of PSO are proposed, so detailed surveys of swarm intelligence algorithms and some popular algorithms are carried out.

2.1  Swarm Intelligence (SI)

Swarm intelligence (SI) [9-13] is briefly defined as the collective behaviour of decentralized and self-organized swarms. The well-known examples for these swarms are bird flocks, fish schools and the colony of social insects such as termites, ants and bees. The individual agents of these swarms behave without supervision and each of these agents has a stochastic behaviour due to her perception in the neighbourhood. The intelligence of the swarm lies in the networks of interactions among these simple agents, and between agents and the environment. SI is becoming increasingly important research area for computer scientists, engineers, economists, bioinformatics, operational re-searchers, and many other disciplines. This is because the problems that the natural intelligent swarms can solve (finding food, dividing labour among nest mates, building nests etc.) have important counterparts in several engineering areas of real world [14]. Few important approaches which are based on ant colony and bird flocking are called ant colony optimization (ACO) [15-16] and particle swarm optimization (PSO) [17, 18]. These techniques have been applied to a wide variety of applications. Now we discuss some important swarm optimization techniques in detail.

2.2  Ant Colony Optimization (ACO)

Ant Colony Optimization algorithms is Swarm Intelligence methods which was proposed [19, 20] by Marco Dorigo in 1992 in his PhD thesis. It is a probabilistic technique for solving computational problems which can be reduced to finding good paths through graphs. The main idea was inspired by the behaviour of real ants. In the natural world, ants (initially) wander randomly, and upon finding food return to their colony while laying down pheromone trails. If other ants find such a path, they are likely not to keep travelling at random, but to instead follow the trail, returning and reinforcing it if they eventually find food. Thus, when one ant finds a good (i.e., short) path from the colony to a food source, other ants are more likely to follow that path, and positive feedback eventually leads to all the ants’ following a single path. The idea of the ant colony algorithm is to mimic this behaviour with "simulated ants" walking around the graph representing the problem to solve. In ACO a colony of artificial ants collectively works to find an optimal solution for a discrete problem [21-23]. ACO was the first algorithm, aiming to search for an optimal path in a graph, based on the behaviour of ants seeking a path between their colony and a source of food. ACO can’t perform well in large search space and criticized due to their slow performance.

2.3  Artificial Bee Colony (ABC)

Artificial Bee Colony algorithm (ABC) [24-27] was proposed by Karaboga in 2005, based on the intelligent behaviour of honey bee swarm. In the ABC model, the colony consists of three groups of bees: Employed Bees, Onlookers, and Scouts. For every bee in the hive there can be two possibilities [28]:

1. She can be a scout, searching for the food (probable solution) in random directions or
2. She will become employed once she finds the food or if she finds the location of a food from another scout. Employed bees chase their food source and return back to hive and start dancing near hive. The employed bee becomes a scout if her food source has been deserted.

The nectar information shared by employed bees is used by the onlooker bees to choose a food source according to its nectar (fitness) amount. They select one of the food sources whose corresponding nectar is highest [29-30].

2.4  Introduction to Particle Swarm Optimization (PSO)

PSO is a robust optimization technique that applies the social intelligence of swarms to solve optimization problems. Bird flocking and fish schooling are the example of swarm intelligence. In bird flocking, each swarm update its position by following collective intelligence of the group and its own intelligence. First version of this algorithm was proposed by J. Kennedy, R. Eberhart [17].In this version, a set of potential solutions (called as particles), are dispersed at various points in the solution space. Each point has some objective function value, and thus has fitness, for its current location. Each particle’s movement is influenced by the following two factors:

1. The best fitness achieved by the particle so far. (BFS)
2. The best fitness achieved by any particle in the neighbourhood.  (BFN)

Suppose that if the search space is n-dimensional, and then the particle i of the swarm can be represented by an n-dimensional vector Xi= (xi1, xi2, …,xin). The velocity of this particle can be represented by another n-dimensional vector Vi= (vi1, vi2, …, vin). The fitness of each particle can be evaluated according to the objective function of optimization problem. The best previously visited position of the particle i is noted as its individual best position Pi= (pi1,pi2,

…,pin). The position of the best individual of the whole swarm is noted as the global best position G= (g1,g2, …,gn). At each step, the velocity of particle and its new position will be assigned according to the following two equations:

Vi=ω∗Vi+c1∗r1∗(Pi-Xi)+c2∗r2∗(G-Xi)                                                                                  (1)

Xi=Xi+Vi                                                                                                                                                                                                   (2) Where, ω is called the inertia weight that controls the impact of previous velocity of particle on its current one. r1, r2 are independently uniformly distributed random variables with range (0, 1). c1, c2 are positive constant parameters called acceleration coefficients which control the maximum step size. In PSO, Eq. (1) is used to calculate the new velocity according to its previous velocity and to the distance of its current position from both its own best historical position and the best position of the entire population or its neighbourhood. Generally, the value of each component in V can be clamped to the range [-vmax, vmax] to control excessive roaming of particles outside the search space. Then the particle flies toward a new position according Eq. (2). This process is repeated until a user-defined stopping criterion is reached.

2.5  Variants of PSO Algorithm

PSO variants are as follows:

2.5.1  Discrete PSO

Discrete PSO algorithm [31-32] is applied to discrete and combinatorial optimization problems over discrete-valued search space. In this algorithm, particle’s positions [33] are discrete values. The velocity and position equation are developed for real (discrete) value and updated in each iteration. In a more general case, when integer solutions (not necessarily 0 or 1) are needed, the optimal solution can be determined by rounding off the real optimum values to the nearest integer. Discrete PSO has a high success rate in solving integer programming problems even when other methods, such as Branch and Bound fail [34]. It has a quick convergence and better performance results [35].

2.5.2  Binary PSO

In binary PSO [36], each individual (particle) of the population has to take a binary decision, either YES/TRUE = 1 or NO/FALSE = 0. Each particle represents its position in binary values which are 0 or 1. Each particles value can then be changed from one to zero or vice versa. In

this algorithm velocity must be [37] restricted (normalized) within the range [0, 1]. The velocity vector equation and position vector equation are defined as:

vin(t+1)= (3)

    (t+1)={                       .                                                                                                    (4)

2.5.3  Neighbourhood Guaranteed Convergence PSO (GCPSO)

Neighbourhoods GCPSO model the structure of social networks [38]. Implementing neighbourhoods in the standard PSO requires replacing the velocity update with the following: vi(t+1) =X(vi(t)+ c1r1(pbest(t)-xi(t))+c2r2(gbest(t)-xi(t))) (5) Where, gbest is the best position found so far in the neighborhood of the ith particle unlike the entire swarm. The purpose of neighbourhood is to preserve the diversity within the swarm by impending the flow of information through the network. Neighborhood topologies such as lbest with k = 2 provide a very slow flow of information via a long directed path. This allows particle to explore larger areas of search space without being immediately drawn to the global best particle.

2.5.7  NSPSO

A new PSO algorithm called PSO with neighbourhood search strategies (NSPSO), which utilizes one local and two global neighbuorhood search strategies is defined by Yao, Jingzheng et al. [39]. The NSPSO includes two operations. First, for each particle, three trial particles are generated by the above neighbourhood search strategies, respectively. Second, the best one among the three trial particles and the current particle is chosen as the new current particle.

2.5.8  IEPSO

In Immunity-enhanced particle swarm optimization, IEPSO [40], a population of particles is sampled randomly in the feasible space. Then the population executes PSO or its variants, including the update of position and velocity. After that, it executes receptor editing operator (non- uniform mutation) according to a certain probability pr, and vaccination operator according to probability pv. The new generation is obtained by the selection operator after the flying of particles and two immune operators receptor editing and vaccination.

2.6 Parameter Tuning in PSO Algorithms

The challenge of identifying appropriate parameters for efficient performance of particle swarm optimization algorithms has been studied for many years. In this approach, the parameters of the PSO algorithm (inertia weight, cognitive acceleration coefficient and social acceleration coefficient) are tuned for improving the optimal solution in the search space [41-44]. Parameter tuning strategy is needed because the basic version of the PSO algorithm was not giving efficient performance on the benchmarks functions. Proper and fine tuning of the parameters may result in faster convergence of the algorithm, and alleviation of the local minima. Initially, the values of the parameters of PSO algorithm were constant. However, experimental results proved that it is better to initially set the parameters to a large value, in order to promote global exploration of the search space, and gradually decrease it to get more refined optimal solutions [42, 45]. A large parameter’s value facilitates global exploration (searching new areas), while a small one tends to facilitate local exploration (fine tuning of the current search area). A suitable value for the parameters usually provides balance between global and local exploration abilities and consequently results in a reduction of the number of iterations required to locate the optimum solution [44].

2.6.1 PSO - Time Varying Inertia Weight (PSO-TVIW)

For most of the problems, Shi and Eberhart [46] have observed that the performance of the PSO algorithm can be improved by varying the value of inertia weight from Imax at the beginning to Imin at maximum number of iterations. The equation of the inertia weight is as follows -: w =wmin+ (wmax -wmin)(                        )                                                                                      (6) Where wmin = 0.4 is minimum value of inertia weight. wmax = 0.9 is maximum value of Inertia weight. Imax is the maximum number of iteration. Icurrent is the current iteration.

2.6.2  PSO - Random Inertia Weight (PSO-RANDIW)

PSO-TVIW  method  is  not  very  effective  in  tracking  dynamic  [47]  environment.  Shi  and Eberhart proposed random inertia weight factor to track dynamic environment.

The inertia weight changes randomly according to the following equation -: w =0.5 +

(7)

Where, r is a uniformly distributed random number between 0 and 1.

2.6.3  PSO - Time Varying Acceleration Coefficients (PSO-TVAC)

The objective of the PSO-TVAC algorithm is to enhance the global search in the early part of the optimization and to encourage all the particles to converge toward the global optimum at the end of the search. In this algorithm the inertia weight, the cognitive acceleration coefficient and the social acceleration coefficient [48-50] are change according to the following equations -: c1 =c1min+ (c1max -c1min) (                        )                                                                             (8) c2 =c2min+ (c2min –c2max) (                        ) (9) w=wmin+(wmax-wmin)(                      ) (10) Where c1min = 0.5 is minimum value of c1. c1max = 2.5 is maximum value of c1. c2min = 0.5 is minimum value of c2. c2max = 2.5 is maximum value of c2. The performance of the algorithm is improved by varying c1 from 2.5 to 0.5, c2 from 0.5 to 2.5 and w from 0.9 to 0.4 over the full range of the search space.

Chapter3

Proposed Method

PSO (Particle Swarm Optimization) is very popular and is inspired from social behaviour of bird flocking or fish schooling. It is a population based optimization algorithm that optimizes a problem by updating the velocity and position of each particle according to simple mathematical formulae. Each particle’s movement is influenced by its personal best (pbest) position and global best (gbest) position. The values of pbest and gbest are updated in each generation. The performance of PSO depends on many factors in which parameter tuning plays a major role. Tuning of random parameters is very important issue and if properly done, it can avoid premature convergence of PSO on local optimal solutions. Many papers [51-53] suggested solution of this issue by giving various methods to tune random parameters (Like w, c1, c2, r1 and r2). The performance of PSO can be improved by redesigning its operators. When we design new version of PSO, We have to analyze the result of adding same factor to each particle, whether it moves the particle towards the global optimal solution or force to get stuck in local optima. For this, it is required to add new factor acceleration (ac) in velocity vector that stores the information, whether the particle moves in the right direction or not. The velocity of the particle changes (increasing or decreasing) according to observation stored by factor ac. Also it is required to minimize the distance between the pbest (personal best position) position of the particles and gbest (global best position) position of the particles as the number of generation increases. It helps particle to converge its search towards the global optimal solution efficiently. The distance between the particles’ pbest and gbest is inversely proportional to the current iteration. This  thesis  implements  a  modified  particle  swarm  optimization  algorithm  named  as “Modified  time  varying  acceleration  coefficient  based  PSO  (PSO-MTVAC)”  in  which

additional parameter “acceleration to particle (ac)” is included in velocity vector, which causes the PSO to converge towards the optimal solution very fast. Also we have minimized the distance between the personal best and global best position of the particles by minimizing the angle (dt) between pbest and gbest of the particles. The angular distance between the particles pbest and gbest can be seen in the following figure 1. The aim of this thesis is to solve global optimization problem. 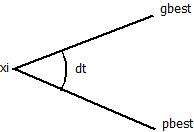Figure 1: Representation of the Angular distance between particle’s positions.

3.1  Proposed Approach

The purpose of any optimization algorithm is to obtain the global optimal solution in minimum iteration and avoid premature convergence. The proposed algorithm “Particle Swarm Optimization Modified Time Varying Acceleration Coefficient (PSO-MTVAC)” is designed to obtain these requirements. To efficiently convergence towards the optimal solution, the parameters ω, c1, c2 of the PSO algorithm are varying according to the given equation mentioned below to minimize the angle (distance) between pbest and gbest of the particles. Also a new factor α is added in the velocity vector to store the information during the previous generations that helps to manage (increase or decrease) the velocity of the particle. The addition of factor α is significant because in PSO, particle updates its position only on the basis of its current position and its current velocity. And information stored in the previous generations is lost. Thus storing the information of previous generation helps to improve the convergence rate of the algorithm. The parameters are mathematically represented as follows: c1= c1min + cos (dt) α * (c1max − c1min)                                                                        (11) c2= c2max + sin (dt) β * (c2min − c2max)                                                                         (12) ω = ωmin+ cos (dt) γ * (ωmax − ωmin)                                                                          (13)

Where dt (angular distance between pbest and gbest) is defined as follows: dt = (Imax – Icurrent)/Imax The calculation of new velocity vector and new position vector of the particle is as follows:

vi1  * vi c * r( p

• x) c

* r(g

• xi) ac

(14)

j i1   j 1 1 j j i  i1 2 2 best j

xj xj vj (15)

Where id = 1, 2, 3, …, i. Minimum and maximum values of cognitive and social acceleration coefficients are 0.5 and 2.5 respectively. For minimum c1min = c2min = 0.5 and for maximum c1max = c2max = 2.5. Minimum and maximum values of inertia weight are 0.4 for ωmin and 0.9 for ωmax. Constant coefficient α, β and γ are used whose values are 1.1, 1.4 and 0.4 respectively. In the proposed algorithm, position and velocity is assigned to particle randomly. In further generations, adjustment of the particle’s velocity is conducted by comparing the fitness of new position of the particle and its previous best position (pbest) in respect to global best position (gbest) of all particles. If the new position obtained by a particle is found better than the previous pbest then the particle’s velocity decreases and it helps to exploit the solution in this newly found good region else it exploit the region around previous pbest to obtain new solutions. In the proposed method, the inertia weight and the cognitive acceleration coefficient starts with its minimum value ωmaxand c1maxwhen the number of iteration is 0 (Icurrent= 0) and gradually decreases in a non-linear fashion to its minimum value of ωminand c1minwhen current iteration is equal to maximum iteration (i.e. when Icurrent= Imax). This will encourage all particles to search around the entire search space and latter iteration it will converge towards the global optimum. Initially, the particles are randomly generated with random position and velocity vector in the nth dimensional search space. Fitness value of all particles is evaluated. Choose pbest of all particles and initialize fitness value to them. Set the value of parameters and maximum number of iterations. In each iteration, fitness of all particles is evaluated and each particle updates its velocity and position according to the equation 14 and 15. If the current iteration is equal to the specified number of generations then set the global best position of the swarm is the optimal solution.

3.2  Proposed Algorithm (Pseude Code)

Input:

•      pop = size of population
• dim = dimension
• f(x) = fitness function with constraints
• Imax= maximum iteration.

Output:

• Optimum fitness value of function f(x)
•   The global best position of the swarm at which optimum value is found. For each particle of ithpopulation

1. Randomly initialize the position vector xjof dim. 2.  Randomly create a population (pop) of velocity vectors vjof dim. 3.  Initialize the parameters as given below: c1min= c2min= 0.5 c1max= c2max= 2.5 ωmin= 0.4 and ωmax = 0.9. Constant coefficient α = 1.1, β = 1.4 and γ = 0.4

4. Evaluate fitness of individual f (xj).

5. Choose personal best Pjand initialize it with fitness value.

6. For i = 1 to Imax.

7. Set the parameters of algorithm as follows: c1 = c1min+ cos (dt) α * (c1max− c1min)

c2 = c2max+ sin (dt) β * (c2min− c2max) ω = ωmin + cos (dt) γ * (ωmax− ωmin)

8. For j = 1 to pop.

9. Find personal best Pj.

if f(xj) < Pjpj=xj Find global best gbest if f(xj) < gbest gbest = xj.

10. Initialization of initial velocity of particle as:

i   vi

11. Update the velocity (vj) of particle:

vi1  * vi c * r(P

• xi) c

* r(G

• xi) ac

j j 1 1 j j 2 2 best j

12. Evaluate acceleration of particle:

aci1 vi1

• ui

13. Update the position vector (xi1 )
    j
    j
    j

of particle:

xi1  i i1 j

14. Step 7 to step 13 is repeated, until the termination criteria is met i.e j =pop.

15. Step 6 to step 15 is repeated, until the termination criteria is met i.e. i = Imax).
16. The global best position of the swarm is the optimal solution.

Chapter4

Experiment & Results

4.1  Experimental Setup

The Black-Box Optimization Benchmarking (BBOB) provides twenty four noise free test- bed, real-parameter single objective benchmark functions [54-55] which are used to evaluate the performance of PSO_MTVAC in terms of optimum solutions after a predefined number of generations and the valid convergence rate to the optimum solution. Search domain [-5, 5] is taken for all 24 benchmark functions. These benchmark functions for the experiment are scalable with dimension and fifteen instances are generated for each benchmark function. These functions are classified in five groups include separable functions (f1 - f5), functions with low or moderate conditioning (f6 - f9), unimodal functions with high conditioning (f10 - f15), multi-modal functions with adequate global structure (f16 - f19), and multi-modal functions with weak global structure (f20 - f24). All benchmark functions are scalable with the dimension (D). Most functions have no specific value of their optimal solution i.e. they are randomly shifted in x-space. All functions have an artificially chosen optimal function value i.e. they are randomly shifted in f-space. Since for separable functions the search process can be reduced to D one-dimensional search procedures, non-separable functions are much more difficult. Other than first group functions (f1 - f5), the rest benchmarks functions

are non-separable. Description of benchmark function considered for test-bed is shown in the following table 4.1: Table 4.1: BBOB Benchmark function used for experimental work.

Group	f#	FunctionName
Separable	f1	Sphere
	f2	Ellipsoidal
	f3	Rastrigin
	f4	Büche-Rastrigin
	f5	Linear Slope
Low or moderate conditioning	f6	Attractive Sector
	f7	Step Ellipsoidal
	f8	Rosenbrock, original
	f9	Rosenbrock, rotated
Unimodal with high conditioning	f10	Ellipsoidal
	f11	Discus
	f12	Bent Cigar
	f13	Sharp Ridge
	f14	Different Powers
Multi-modal with adequate global structure	f15	Rastrigin
	f16	Weierstrass
	f17	Schaffers F7
	f18	Schaffers F7, moderately ill-conditioned
	f19	Composite Griewank-Rosenbrock F8F2
Multi-modal with weak global structure	f20	Schwefel
	f21	Gallagher’s Gaussian 101-me Peaks
	f22	Gallagher’s Gaussian 21-hi Peaks
	f23	Katsuura
	f24	Lunacek bi-Rastrigin

These functions are used to analyse the performance of the proposed algorithm with other algorithms. For each functions we have executed 15 instances. For experimental work we have taken population size = Dimension * 40 with dimensionality 2, 3, 5, 10. Total number of function’s evaluation is made dependent on the dimension and it varies as the dimension changes. To calculate the function evaluation formula dimension* 105 is used. The total function evaluation is calculated by the formula Totalfunctionevaluation=Maximumfunctionevaluation*Functionevaluationinoneiteration.Where Maximumfunction

evaluation= (300*dim) +500.The data set which is used to compare the performance of the proposed algorithm has been taken from the COCO framework [56].

4.2  Simulation Strategy

Simulation is carried out to check the quality of optimum solution and convergence rate of the newly introduced method in comparison with eleven state-of-the-art algorithms. The term Expected Running Time (ERT) is the time defined as the expected number of function evaluations to reach a target function value for the first time, applied in the figures and tables, are dependent on a given target function value (ft), and it is denoted by ft=fopt+∆f, where ∆f=10-8, it is computed over all relevant trials as the number of function evaluations executed during each trial. #succ denotes the number of trials which is important to achieve to reach the final target ft.In the experiment the rank-sum test is used to test the statistical significance for a given target ∆ftand this is used for each trial, either the number of required function evaluation to achieve the ∆ft(inverted and multiplied by -1), or, if the target was not reached, the best ∆fvalue achieved, measured only up to the smallest number of overall function evaluations for any unsuccessful trial under consideration if available.

4.3  Symbols, Constants, and Parameters

• D = 2, 3, 5, 10, 20, 40 is search space dimensionalities. It is used for all 24 benchmark functions.
• Ntrial is used as the number of trials for each function and dimensionality. It determines the least possible measurable success rate and also determines the overall CPU time. When we have compared to a standard setup for testing stochastic search procedures, Ntrial = 15, a small value have chosen for evaluating the performance over all trials. Therefore, single trial can be longer within the same CPU-time budget

and does more function evaluations until or unless ftarget is obtained. If an algorithm

terminates itself before reaching the ftarget, then longer trials can takes place by independent multi starts and help an algorithm to reach the ftarget. More sophisticated restart techniques are executable because multi starts are conducted within each trial.

• ∆f= 10-8 precision to reach the target value from fopt.

• ftarget = fopt + ∆fis the target function value to reach for different ∆fvalues. The final, smallest considered target function value is ftarget = fopt + 10-8, but also larger values for ftarget are evaluated.

4.4  Used Notations

∆f precision to reach, i.e., a difference to the optimal function value foptand foptis the optimal function value defined for each benchmark function individually. ftargetis the target function value to reach the optimal value. The smallest specified final target value is ftarget= fopt+ 10-8, but also larger values of ftargetare evaluated. Ntrials is used in this paper for each function and dimensionality individually for each single setup. D indicates the search space dimensionality used for all functions. D = 2, 3, 5, 10.

4.4 Dimension Wise Results

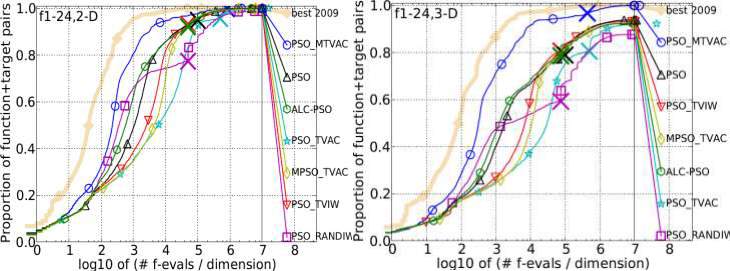
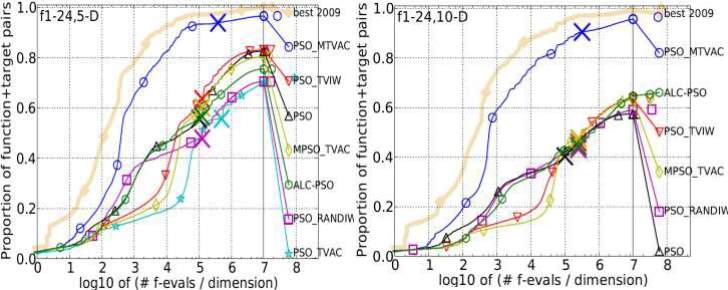The overall performance of the proposed PSO_MTVAC for all 24 benchmark functions with dimension size 2D, 3D, 5D and 10D is as follows:

Figure 4.1: Bootstrapped empirical cumulative distribution of the number of objective function evaluations divided by dimension for 50 targets in 10[-8…2] for all 24 benchmark functions listed in table 4.1 and subgroups in 2-D, 3-D, 5-D, 10-D. The “best 2009" line corresponds to the best Expected Running Time (ERT) observed during BBOB 2009 for each single target. In the above mentioned figure 4.1, we can see that the proposed PSO_MTVAC gives better result than PSO and its variants. The result shows that the proposed algorithm performs well in solving both uni-modal and multi-modal problems.

4.4.1  Function and Dimension Wise Performance

• SeparableFunction:There are five separable functions such as Sphere function, Ellipsoidal function, Rastrigin function, Büche-Rastrig in function and Linear Slope function having similar nature are used to check the accuracy of EAMD. It is found that performance of PSO_MTVAC is compared with other is not good. We have obtained mixed result. Result for all five functions is shown as follows:

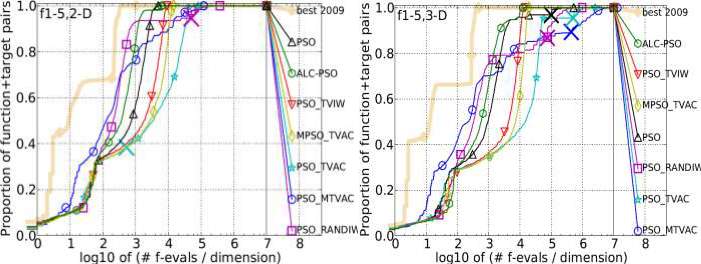
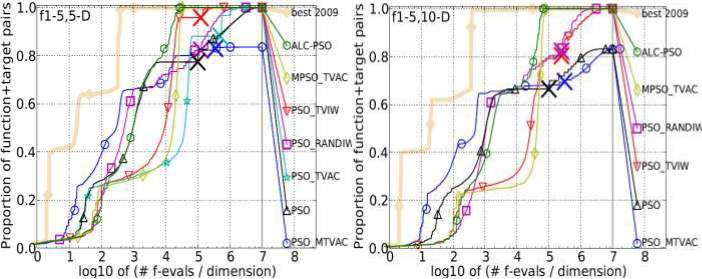Figure  4.2:  Bootstrapped  empirical  cumulative  distribution  of  the  number  of  objective function evaluations divided by dimension for 50 targets in 10[-8…2] for all 5 •              Separable Function listed in table 4.1 and subgroups in 2-D, 3-D, 5-D and 10-D. The “best 2009" line corresponds to the best Expected Running Time (ERT) observed during BBOB 2009 for each single target.

• LoworModerateConditioningFunctions:It is a group of four separable functions like Attractive Sector function, Step Ellipsoidal function, Rosenbrock, original function, and Rosenbrock, rotated function. It is found that for all dimensions 2, 3, 5 and 10 PSO_MTVA dominates all variants of PSO and secured 2nd  position among

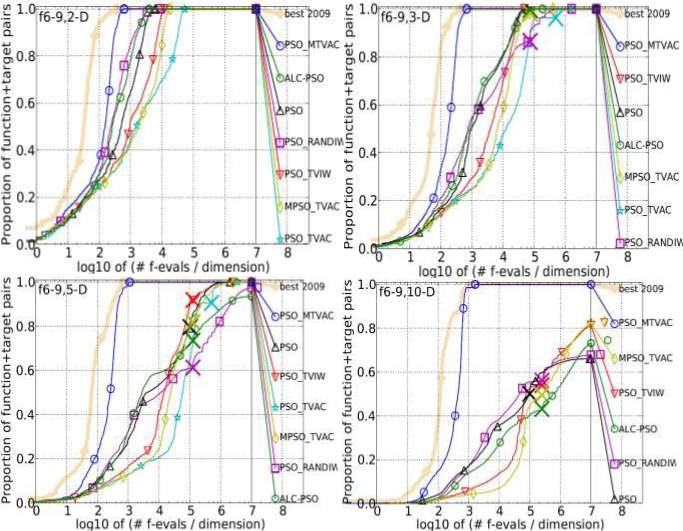eight algorithms. So, the overall performance is very good and it shows its positive growth to reach the high accuracy. Results are as given below: Figure 4.3: Bootstrapped empirical cumulative distribution of the number of objective function evaluations divided by dimension for 50 targets in 10[-8…2] for all 4 • Low or Moderate Conditioning Functions listed in table 4.1 and subgroups in 2-D, 3-D, 5-D and 10-

4. The “best 2009" line corresponds to the best Expected Running Time (ERT) observed during BBOB 2009 for each single target.

           Unimodal with High Conditioning Functions

Ellipsoidal function, Discus function, Bent Cigar function, Sharp Ridge function and Different Powers function, comes under the group of unimodal with high conditioning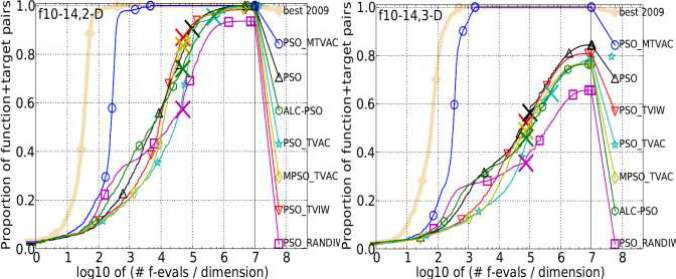

functions. The convergence rate and performance accuracy is checked over this group of functions and it is found that PSO_MTVAC has secured 2nd position in comparison to other algorithms in dimensions 2, 3 and 5. In dimension 10, it has secured 1st position which shows its capability and accuracy towards finding global optimal solution. So, as the performance is concerned, it shows its positive growth to reach the required accuracy.  The results are as follows: 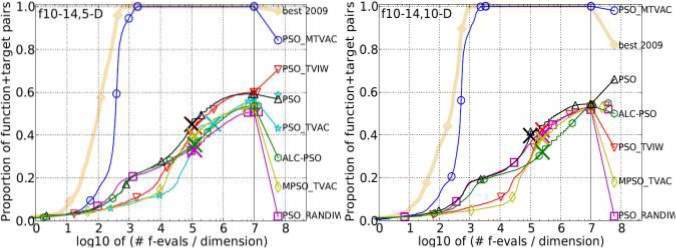Figure 4.4: Bootstrapped empirical cumulative distribution of the number of objective function evaluations divided by dimension for 50 targets in 10[-8…2] for all 5 Unimodal with High Conditioning Functions listed in table 4.1 and subgroups in 2-D, 3-D, 5-D and 10-D.

The “best 2009" line corresponds to the best Expected Running Time (ERT) observed during BBOB 2009 for each single target.

         Multimodal Functions with Adequate Global Structure

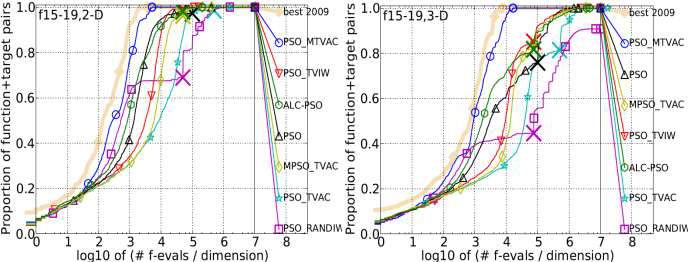Rastrigin, Weierstrass, Schaffers F7, Schaffers F7 moderately ill-conditioned, and Composite Griewank-Rosenbrock F8F2 functions are the group of five functions on which the convergence rate and the performance accuracy of PSO_MTVAC has checked. It is found that it has obtained better results shown in figure 4.5 in comparison to other algorithms on different dimensions. PSO_MTVAC has obtained 2nd position for all dimensions and shows its superiority over other algorithms. 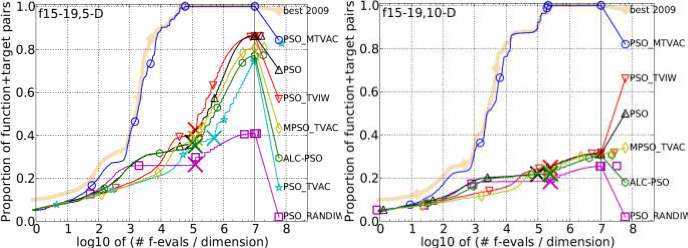Figure  4.5:  Bootstrapped  empirical  cumulative  distribution  of  the  number  of  objective function evaluations divided by dimension for 50 targets in 10[-8…2]  for all 5 Multimodal

Functions with Adequate Global Structure listed in table 4.1 and subgroups in 2-D, 3-D, 5-D and 10-D. The “best 2009" line corresponds to the best Expected Running Time (ERT) observed during BBOB 2009 for each single target.

           Multimodal Functions with weak global structure

It is a group of five functions: Schwefel function, Gallagher’s Gaussian 101-me Peaks function, Gallagher’s Gaussian 21-hi Peaks function, Katsuura function and Lunacek bi- Rastrigin function. PSO_MTVAC is analysed on these functions one by one and comparison is done with other algorithms. In dimensions 2 and 3, it has secured 5th and 2nd  position while in dimension 5 and 10 it has obtained 1st  position among all eight algorithms. So, the overall result is very good and it shows its outstanding performance for multimodal functions. The growth rate towards getting the optimal solutions in feasible generations is very impressive. It has dominated all algorithms including best 2009 of COCO framework. These results are given below.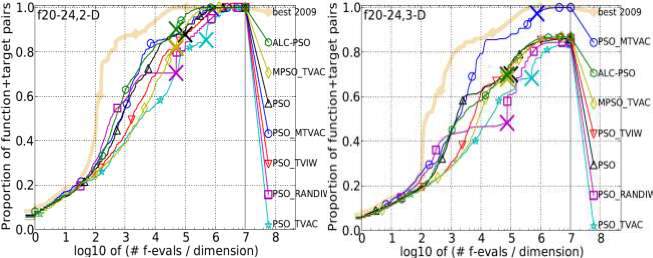

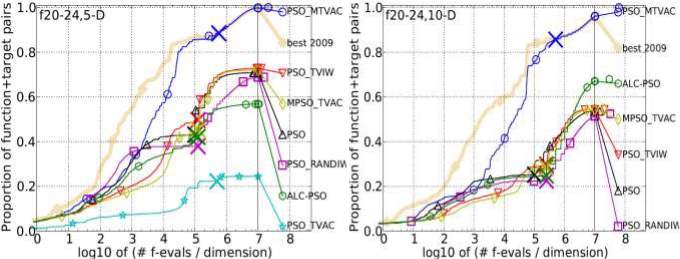Figure 4.6: Bootstrapped empirical cumulative distribution of the number of objective function evaluations divided by dimension for 50 targets in 10[-8…2] for all 5 Multimodal Functions with weak global structure listed in table 4.1 and subgroups in 2-D, 3-D, 5-D and 10-D. The “best 2009" line corresponds to the best Expected Running Time (ERT) observed during BBOB 2009 for each single target.

Chapter5

Conclusion and Future Work

5.1  Conclusion

Seven different state-of-the art algorithms have been used to check the performance of PSO_MTVAC algorithm. The benchmark functions used for the experimental work are categorized into two parts i.e. unimodal and multimodal. In unimodal, functions have three groups such as separable functions, moderate functions and ill-conditioned functions and each group contains five different functions except moderate functions group which contains four functions. Multimodal functions are categorized into two group i.e. multimodal functions and weakly structured multimodal functions. It also contains five different functions in each group. The “all functions” category is used to check the overall performance of the proposed algorithm on all functions (1-24) together. Performance of PSO_MTVAC is checked over four different dimensions like 2-D, 3-D, 5-D, and 10-D. In every dimension PAO_MTVAC has shown its superiority over other algorithms. A modified version of PSO_TVAC is proposed to improve the convergence rate of this algorithm. This modification is done by updating the velocity vector and parameter tuning of existing PSO_TVAC algorithm. From the results it is clear that on dimension 2 the performance of PSO_MTVAC has improved over PSO_TVAC and other existing algorithms on multimodal functions. However its convergence rate has decreased in separable functions. Similarly the convergence of PSO_MTVAC has improved in multimodal functions of 3 dimensions. In Unimodal with High Conditioning Functions, PSO_MTVAC has dominated best 2009 and all variants of PSO in 10 dimensions. Also in dimensions 5 and 10, PSO_MTVAC has dominated best 2009 and all variants of PSO in Multimodal Functions

with weak global structure. Overall performance of PSO_MTVAC is outstanding and it proves its accuracy for unimodal and multimodal problems. This version has good convergence rate on all dimensions.

5.2  Future Work

We have observed many future scopes during working in this area. This can be applied on various real life applications, such as software cost estimation, minimize the cost and energy dissipation in wireless sensor network, energy minimization problem in RNA secondary structure, protein folding problem etc.