Research Project on the Creation of a Mechanical Synthesizer

ABSTRACT

Applying harmonic mathematical theorem to the construction and manufacturing of a unique mechanical synthesizer instrument. 

In the majority of world cultures, music is an essential part of everyday life. The importance of music is often praised, however the means in which we produce this music is equally significant. The study, construction and classification of instruments is named organology.

This research project is a study focused on implementing the ideas of past instruments to create a fully mechanical synthesizer. The research question posed is whether – with the application of mathematical theorem and the relationship it has with music – it is possible to construct an instrument that produces musical tones from mechanical means. The problem with previous research lies in the lack of physical examples of these theories.

However, this project amends this lack of knowledge. This approach of applying organology to mathematics is inherently unique as there is no mechanical instrument that uses mathematics as its foundational properties. In order to understand and realise this goal, research into the history of the synthesizer; mathematics and the physics of sound and tuning systems will take place in this study. It is hoped this study will bridge a gap between theoretical knowledge and practical organology.

Synthesisers: Then and Now

History of synthesisers

The synthesiser is a staple in today’s modern music. With such an emphasis on electronic sounds in pop music of the last three decades, it is hard to argue that without synthesisers, music would be the same today. Synthesisers range from the more common drum machines and keyboard based instruments to the less conventional modular systems and the more experimental models such as the Theremin. In basic terms, the ‘Synthesiser’ can be defined as an instrument that can produce, shape and control sound, usually from an electronic source. (Merriam-Webbster , 2017)

Although considered a modern instrument, early versions of the synthesiser have been around since the late 19th century. Starting it all was the Telharmonium, built by Thaddeus Cahill in 1896, which weighed two-hundred tonnes. Although impractical, it was the first of its kind. Years later, in 1919, Russian inventor Leon Theremin invented the synth – the Theremin – that was used widely for sci-fi films in the 20th century. This is one of the earliest examples of a synthesiser utilising something different playing surfaces to dictate sound. (Apple, 2017)

In the 1920-30’s, alternative methods of sound synthesis were invented by Pavel Tager and Alexander Shorin. They invented a method called ‘graphical sound’ which used light to synthesise sound. (Smirnov, 2011) This is an example of the ways pioneers were experimenting with an eclectic mix of methods to produce new options for synthesis. While these examples may not be referred to explicably as synthesisers by their contemporaries at the time, they are still by modern definition exactly that.

Three decades after drawn sound, in the 1960’s, the first version of the modern and most popular synthesiser – which used a traditional keyboard – was created by Bob Moog using voltage control for sound synthesis. At the same time, Don Buchla was focusing on developing and honing the modular synth, which was less comprehensible for musicians than its competitor as it lacked a keyboard. (Critical Angst, 2015)  What it lacked in approachability was more than compromised for with its sheer power as an instrument and its customisability. Both Bob Moog and Don Buchla are considered synth pioneers in both keyboard and modular models respectively. (I Dream of Wires, 2014)

During the next four to five decades, the two pioneers produced their competing visions of the synthesiser. Some refer to it as the earlier East Coast/West Coast music rivalry. Moog synthesisers were dubbed “East coast” and Buchla synthesisers “West Coast.” (Tkacs, 2010, p. 10)

The Telharmonium

The Telharmonium is widely considered the first synthesiser. (Crab, 2014) It was built in 1897 by Thaddeus Cahill and much like the first computers, it was incredibly cumbersome. To transport the instrument from Washington D.C to New York City, more than twelve railway boxcars were needed. (Chadabe, 2001) The Telharmonium was so heavily uncompromising as Cahill’s goal was to create an instrument that could reproduce the sound and timbre of any other instrument.

This would be done by using electrical signals to replicate harmonics. In order to achieve this goal, the instrument needed to be this size. In his vision, it would have the sounds of all instruments with the drawbacks of none. Cahill then hypothesised that such an electrical instrument could have the power to send music anywhere electrically. (Weidenaar, 1995, p. xiv)

With this vision in mind, he created the first model and submitted his patent for the Telharmonium as:  “The Art of and Apparatus for Generating and Distributing Music Electrically” in 1895. It was rejected initially but an official patent was composed in 1897. (Crab, 2014) The Telharmonium was designed to be used as a method of electromagnetically synthesising and distributing music over the new telephone networks of Victorian America.

Interestingly, Tahill figured that if he could send music through the telephone at the relevant volume, he could start a business supplying music to public places such as hotels, restaurants, and even private homes. Consequently, Cahill was the pioneer of what we know today as “Muzak”.(Williston, 2000)

The Telharmonium worked through a fairly simple method revolving around the use of spinning cogs. When these cogs were rotated, a magnetic coil would be held close to the teeth. The closer the teeth were to the coil, a stronger current of electricity was generated therefore a difference in volume was attainable. (Weidenaar, 1995, p. 31)In between the teeth very little electricity was generated through the coil. This alternating current of electricity is what created the sounds as the push and pull of electrons created a sine wave. (The Telharmonium , 2014) 

Each cog had a differing number of teeth around its circumference, and therefore created different pitches. For example, if the cylinder was rotating at 98 Hz, the section with only a single bump would create a pitch of “G” two octaves below G (392 Hz). The section of the cylinder with two bumps would play an octave higher at G (196 Hz), and the section which contained four bumps would again play the next octave up G (392 Hz), and so on. Seven of these sections resulted in seven octaves of the same note on a single cylinder.

Each cylinder was geared to spin at different speeds. 12 cylinders spinning at different rates allowed the Telharmonium to play the chromatic scale over seven octaves. (Williston, 2000) The dynamics of the notes could be manipulated by increasing and decreasing the distance between the cogs and the coil. Cahill incorporated this feature into the Telharmonium’s playing surface, creating a touch sensitive, dynamic keyboard. (Williston, 2000)

Figure i: The Keyboard system of the Telharmonium. (Crab, 2014)

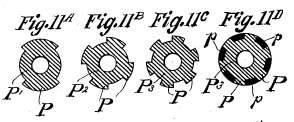
Figure ii: A diagram of Cahill’s tone wheel designs. (Williston, 2000)

The Tonus[1] takes this idea of the spinning electromechanical tone wheels and translates it to a purely mechanical method of sound generation. Each cog spins in a similar fashion to the Telharmonium but instead of the alternating current producing the sound, the physical oscillation of each leather tab will produce a frequency. The Telharmonium is the principle inspiration for the project and builds on the idea of using spinning oscillators as the sound source.

The Theremin

Russian inventor Leon Theremin (born Lev Sergeyevich Termen, 1896), utilized technology in 1919 to develop his first fully functional electronic musical instrument. Originally named the Aetherophone, but later changing to be named after its inventor, the Theremin employed a unique operational configuration. (Dunn, 1992, p. 6) Without touching the instrument, the player controlled pitch through relative proximity of the right hand to a vertical antenna, and volume through similar movements of the left hand in relation to a horizontal antenna. (Theremin, 1924)

The unique method of playing the Theremin has influenced the design of the Tonus. While the Tonus uses a keyboard system, it is not a traditional keyboard design, but rather a unique playing surface.

Drawn Sound

Graphical (drawn) Sound is a technology for synthesizing sound from drawings that was invented in Soviet Russia in 1929 as a consequence of the newly invented sound-on-film technology. This allowed for a form of sound that could be studied and manipulated. (Bencic, 2016, p. 2)  It also opened up the way for a systematic analysis of these traces in such a way that they could be used to produce any sound at will. (Mata, 2013) An example of this is from 1932 in England when – during the production of the film Born to Love – a single line required an overdub. Instead of redoing the scene, they used graphical sound to synthesize a woman’s voice with the new line. This was the work of the young engineer Eric Allan Humphriss (Pelletier, 2017)

Figure iii – Early examples of drawn sound. (Holzer, 2010)

This combination of the mechanical sound source and the electronic pickup has influenced the design of the Tonus. Combing this mechanical element with the rotational cogs and the unique playing surface from both the Telharmonium and the Theremin respectively results in a strong grasp of the ideas that will be employed to the Tonus regarding the method of sound synthesis.

Moog and Buchla: Clash of the Titans

The formulation of new sounds and workflows has always been the object of synthesis. (Rivas, 2016) In particular, two methods have consistently resided on divergent ends of the spectrum. The terms “East Coast Synthesis” and “West Coast Synthesis” are used frequently today – but what exactly do they describe?

Some claim these terms to be misnomers, the argument being that both have shaped modern synthesis to the extent that one can claim it is an amalgamation of both styles. (Rivas, 2016) While this is true, it is important to note that each style — regarding both philosophy and technological layout — is rooted in a different historical context and appeals to differing concerns. (Vail, 2014, p. 245)

The instruments of Robert Moog and Donald Buchla in the 1960s reshaped the potential of the aural landscape and contributed to the foundation for the philosophical and technological development shown in modern synthesizer practice and theory. (Vail, 2014, pp. 17-18)  Buchla began his work in Berkeley, California studying physics while Moog got his start in Trumansburg, New York — this is the origin of the East and West Coast tags. (Bernstein, 2008, p. 163)  Though they were contemporaries, each approached their instrument design from contrasting philosophies and amidst vastly different social settings.

Despite their differences, both Buchla’s and Moog’s approaches were born out of social unrest. New York in the 1960’s was a site of social and political disruption. (Marx, 2011) Poverty was prominent and numerous labour struggles, such as strikes initiated by the United Federation of Teachers, New York City Newspaper Guild, and the Stonewall Riots embodied the harsh realities of the gritty, business-driven atmosphere. (White, 2001)

In some form, the simple and practical East Coast approach shows these qualities in Moog’s aspirations towards efficiency and reliability. Meanwhile, on the West Coast, Buchla was working surrounded by a ‘prevalent counter-culture bent on experimenting with expanded consciousness and alternative lifestyles.’ (Rivas, 2016) The non-traditional, alien sounds that his instruments produced could be seen as a reflection and extension of this experimental culture. (Pinch, 2002, p. 35)

Literature review of Organology and Synthesisers

My project involves the application of mathematics to music and the construction of an instrument, it is important to know the context of the instrument and the research done in the specific field of organology – the science, history and classification of instruments. (Bijsterveld, 2004)

As the instrument that is planned to be made is classed as a synthesiser, it is important to contextualise the project with examples of previous synths and how this project will relate to them. While this is a newer subject area of study, there is still a huge body of knowledge available to research. There are a number of online and academic resources from synthesiser enthusiasts that document the history and development of the instrument. The main online resources that are being used are: ‘Synth Museum’ which is an online encyclopaedia and knowledgebase for vintage synthesisers; ‘Electronic Music Interfaces’ by Joseph Paradiso which is a research project entailing the history of all different subtypes of synthesisers. Finally, the final primary resource is another online knowledgebase with detailed history from 1800 to the modern day. ‘120 Years of Electronic Music’ is a vast library of information on every significant milestone of the instrument’s history.

Alongside these online sources, books by Trevor Pinch, David W. Bernstein and Mark Vail have been used extensively for background context and direct referencing. These books are invaluable for any research into the history of the inventions of Moog and Buchla. These books contain a comprehensive history of both pioneers. While Trevor Pinch focuses on Moog’s work in ‘Analog Days’, David Bernstein steers towards Buchla’s work in ‘The San Francisco Tape Music Centre’.

Although ‘Synth Museum’ and ‘120 Years of Electronic Music’ are both online sources, they can be regarded as reliable bodies of knowledge. All articles are referenced and cited correctly. As the history is objective in this subject, the two sources were cross referenced to find any discrepancies, however none were found. These were also cross referenced with ‘Electronic Music Interfaces’ by Joseph Paradiso and all information was consistent throughout the work. This consistency suggests the reliability of the sources. This information is useful to draw inspiration of the physical design and operation of the instrument. ‘Historical awareness can deepen designers’ understanding of the context they are designing for. In addition, history can spur designers’ imaginations by revealing the contingency of the present situation, rendering it less obvious and inevitable.’ (Wyche, 2006, p. 36) To create something unique, it is important to look to the past, then combine things to create something new.

Maths and Music: A Harmonious Relationship

Frequency and Pitch

In order to build the Tonus, a certain level of mathematical knowledge is required. The research involved focuses on the relationship between maths and music and the applications of this relationship.

A musical scale is a separate set of pitches used in making or describing music. Each pitch corresponds to a certain frequency, expressed in hertz (Hz). A musical scale has an interval of repetition, normally the octave. The octave of any pitch refers to a frequency exactly twice or half of the given pitch. (Benson, 2008, p. 2)

Succeeding octaves are pitches found at frequencies four, eight, sixteen times, and so on, of the fundamental frequency. Pitches at frequencies of half, a quarter, an eighth and so on of the fundamental are the lower octaves of the initial pitch. With information, we can assume the ratio of an octave is 2:1 of the previous octave. (Benson, 2008, pp. 14-25) There is no case in musical harmony where the octave does not follow this rule. Therefore, any note and its octaves will generally be found similarly named in musical systems. (Shah, 2010) This rule makes the octave simple and relatively easy to agree on. However, to decipher the ratios of the notes in between the octaves, a more in depth system will be needed. These are called tuning systems. (Liern, 2004)

Tuning Systems

The Tonus requires a tuning system to relate the ratios of cogs to one another. A tuning system is the set of sounds that music uses. (Liern, 2004) There are four main tuning systems that have been employed in western music over the past two-thousand five-hundred years: Pythagorean tuning, just intonation, meantone / well temperament, and equal temperament. (Ramstrum, 2012) Only two systems were considered for the Tonus: Pythagorean tuning and equal temperament. The reasoning behind this was because these two are arguably the most significant tuning systems.

Pythagorean tuning has been considered by some the root of all mathematics in western harmony and is worth developing ideas around this tuning system. (Barbour, 2004) Pythagoras’ tuning system is based around the ratio of 3:2, which is the untempered perfect fifth – this allows theoretically for octave equivalence. (Milne, 2007) However, with this tuning system there is a note that sounds dissonant. This is known as the “Wolf tone” and is something that can be explained graphically. (Brief History of Western Tuning, 2015) See the diagram below of a root note (D) played up and down perfect fifths using Pythagoras’ ratios. (Brief History of Western Tuning, 2015)

	Ab	Eb	Bb	F	C	G	D(Root)	A	E	B	F#	C#	G#
Freq	206.2	154.7	232	174	261	195.7	293.6	440.4	330.3	495.5	371.6	557.4	418

Down a perfect 5th

Up a perfect 5th

Ab

412.4 Hz

G#

418 Hz

 

Figure IV: Frequencies of Pythagoras’ system and the wolf note. (Nokes, 2015)

Both the G# and Ab are the enharmonic in western harmony, however the frequencies are not the same. This discrepancy creates the out of tune wolf note. (Barbour, 2004, p. 1) The other disadvantage of the Pythagorean tuning system is the differences when modulated into new keys. (Ramstrum, 2012) For this project, this tuning system would not be compatible with the instrument for practical and musical reasons. Firstly, using the Pythagorean system would result in an instrument that was out of tune with other modern instruments and one with less harmonic flexibility.

At the other side of the timeline of western musical tuning, we have equal temperament which is the tuning system used by many instruments today. This system is based on equally dividing the octave ratio of 2:1 into twelve notes. (Brief History of Western Tuning, 2015) This results in “unlimited possibilities of transposition.”(Klerk, 1979)Each note is of equal proportion to each other, hence the name equal temperament.

The first recordings of equal temperament are in the writings of Chinese Prince Chu Tsai-Yü. (Barbour, 2004, p. 7) However, it was later adopted by western musicians in the mid-18th century. (Denton, 1996, p. 5) This new tuning system became the norm and it is still used today.

The Tonus will be based around the equal temperament as this allows the freedom to modulate into new keys. Also, it is the most widely used tuning system which optimises the usability and practicality of the instrument.

The table in figure v shows the ratios of each note in the equal temperament system. These ratios will be applied to the number of teeth on the starting cog to obtain the required teeth for the succeeding cogs in the chromatic scale.

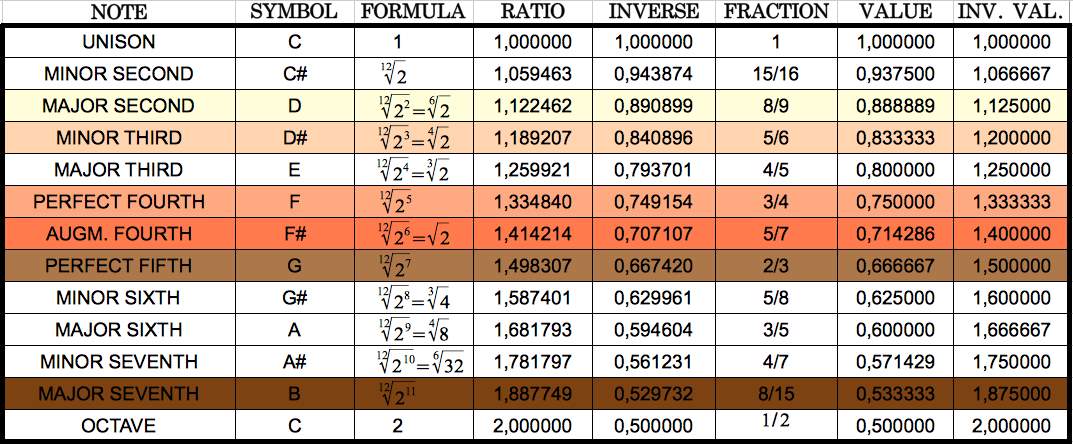
Figure V: A Table of ratios for equal temperament

Literature Review of Maths and Music

To many, maths and music are opposite fields. Music is a creative process that involves a certain amount of subjective input. Emma Ruiz Martín del Campo describes the subject as a “sort of language that makes feasible the expression of imagination, desires, and emotions, which exceed the communication possibilities of other codes like any verbal or pictorial.” (Ruiz, 2006) On the other hand, maths is – for the most part – objective, fact based and generally seen as less creative due to most western experiences at school. However, Eric L. Mann believes “The essence of mathematics is thinking creatively, not simply arriving at the right answer.” (Mann, 2006) In reality, mathematics is everywhere in music. From repeated patterns of musical scales to the frequencies of western harmony, maths is involved and is at the very core of music. Without each other, western music would not be the same. The relationship of mathematics to western musical theory is the main focus of this project and therefore the bulk of research will come from this research field. There are several studies that delve into the relationship between maths and music. It is important to analyse these reports and determine the reliability of the research and find gaps of knowledge. Determining these gaps helps focus the project and result in unique attributes.

For some context, we can break down what is meant by “mathematics in music.” Firstly, it is important to understand the relationship between frequency and pitch. Sound is produces by air molecules vibrating through the atmosphere. Some sounds are inconsistent and lack a pitch – for example, a glass shattering – but some sounds are more consistent and these we know of as pitched sounds – for example, a sine wave. It has been proven that a pitched sound will have a certain fundamental frequency. This frequency is measured in hertz. The number of hertz (abbreviated Hz) equals the number of cycles per second. As frequency increases, perceived pitch also increases. With this in mind, mathematicians can produce formulas for scales by following trends in the frequency of musical notes.

There has been ample research into the mathematical theory of music. While this field is generally scientific and thoroughly researched, there are still parts of research with gaps in which this project will fill. It is generally agreed that pitch is related to the frequency of the waveform. It is also agreed that the amplitude of the wave is directly linked to the volume heard. (Fauvel, 2006, p. 50) This information is the foundation of the project and as such, needs to be a widely agreed opinion. Journal articles from Adam Townsend, John Fauvel and Dave Benson all concur with this information. However, we must analyse their work and the context of the research in order to verify any information.

Adam Townsend’s study named ‘Maths and Music Theory’ is heavily based on the formulaic approach of music and maths and provides a solid emphasis on deep-rooted mathematical ideas. Before the main body of his study, Townsend provides useful background information regarding a short introduction to music theory and the physics of sound. This helps understand the rest of the study and helps contextualize his work. Not only does he break down scales and harmony, but he also explores mathematical theories regarding the composition of music. This is a unique feature compared to other similar works. This extra analysis provides a powerful display of how connected these two subjects are. Because of this, it provides an eclectic bank of knowledge that will ultimately help with the design of the project artefact. Specifically, it covers unknown topics in a mathematical manner such as: harmonics, transposition and inversions. This work is similar to other studies in the same field as it still provides the basic mathematical properties of music in a clear, concise way. The relevance of the information provided in this study comes with the design of the instrument itself, and the fundamental concepts behind its purpose. Although a thorough study, Townsend neglects to provide examples outside of mathematical formulas. Because of this, there is a lack of physical evidence of the theories. However, with the knowledge provided from this study provided a solid theoretical foundation to then take ideas into the physical stage.

Alongside Townsend’s work, John Fauvel’s study ‘Music and Mathematics – From Pythagoras to Fractals’ provides an alternative outlook on similar theories. The largest difference between these two bodies of work is the former focuses on formulas and the latter focuses on graphics and visual representations of complex ideas. The study provides alternative options on how to approach further study in this field. With the added outlook of Pythagoras’ theorems as well as the physics, it is a versatile study with multiple facets to explore. These options provide healthy opportunity to experiment, and hone ideas. The study itself can be considered fairly reliable as it has been edited by multiple people therefore it will have been reviewed more critically than other studies. However, while it provides graphs and charts, there is a lack of unique physical examples. While it does break down certain instruments and their properties, it does not build on these ideas to form ideas for a new instrument.

Benson’s work – specifically this report is essential reading for this project. Benson provides an in-depth analysis of all relevant subjects relating to the field. It ranges from the biology of the human ear, to harmonic frequencies, to deep mathematical explanations. Benson’s work is extremely thorough and will be the main resource for this side of my research. I have included these other studies for intellectual diversity and alternative viewpoints. Some of Benson’s research is not relevant to this project, however this is not a negative thing as it provides background information to further study. Only limited by the lack of the application of these mathematical theories in regard to a musical instrument, Benson’s work is a vast body of knowledge that will be used to further progress the project.

The Tonus: An Explanation and Evaluation

The System of the Tonus

The tonus works by applying simple mathematics to produce frequencies that – when played in series – form a musical scale. These frequencies would be produced by the mechanical oscillators. These oscillators were formed using the mathematic ratios of western harmony and applying the ratios to several cogs. The synth will produce its noise using several leather tabs – one for each cog – that will rub against the spinning cog to produce a vibrating tone. The ratios are from the equal temperament tuning system. This approach is inherently unique to show how sound and pitch can be produced. Visual and aural feedback is instant and provides an applied physical manifestation of the mathematical theory behind music.

Building Process

The building process was the most challenging part of this project. The first stage of the process was to design the mechanical oscillators. Because these cogs would be at the core of the instrument, it was imperative that I made sure these were accurate to the ratios of the chromatic scale. I programmed in a code into Excel to give resulting numbers of a chromatic ratio to find the most accurate starting point for cog one. This resulted in 30 being the most usable number. Bigger and smaller numbers resulted in uneven numbers and too many decimal numbers for use. Using a CAD software, I designed the cogs digitally. For accurate designs, I decided to laser cut the cogs out of acrylic. The acrylic was based on endurance and aesthetics.

The next stage was to build the mount for the cogs. I used a M8 threaded rod with two M8 bolts and washers between each cog. This meant that oscillators could be replaced and moved if necessary. To spin the cogs, I decided to use a belt drive system for smoothness and to keep it quieter than a gear based system. For a clear sound, the cogs would need to spin at a high rate, therefore a brushless motor was needed. To create the least amount of torque required to spin, I used a small belt driver on both ends and a light but strong belt. Next, I needed a way to power and control the motor. I used a 9V battery as it was safe and meant the synth would be more portable – just like Moog’s earlier synths. To control the motor speed, I used a circuit board specifically for changing DC motor speeds. This was to create a “pitch bend” control for increased playability and functionality.

For the casing, I settled on a mahogany wooden stained design. This was to emulate the early models of the Moog synthesisers, which had wooden panels on the sides of the instruments. Wood was also to reduce costs of manufacturing and is easier to shape with limited tools than metal. In regards to the shape of the casing, I again looked to the Moog synthesisers for inspiration. I found the square but sloped side profile look of the Moog sub-37 appealing. I combined this with the boxy aesthetic of the Moog Model D. All panels were cut, sanded, stained, varnished and polished by hand.

With the electronics, I wanted to keep them as exposed as possible for two main reasons. Firstly, I wanted the synth to be as tactile and as palpable as possible. The visual stimulus of seeing where components are connected and how it works instantly incites curiosity – which was a goal of the project. Secondly, I wanted the exposed electronics to be a tip of the hat to Don Buchla and his modular synths – which have the distinguishable look of exposed wiring from patch cables. With elements from both designers, the project ended up having a hybrid look of each company. This in turn could represent the combined roots of modern synths today as it can be argued Moog and Buchla are the fathers of modern synthesizers.

The playing surface was the final element that needed to be added. I knew that a traditional keyboard would not work with the cogs, therefore an alternative method was needed. Because the ratios of the cogs meant that the first key could start on any note and still be chromatic, I needed a uniform playing surface. Taking from Buchla and Theremin, I settled on using a less traditional method of operation. However, I still wanted the approachable playability of the Moog synthesizers. The result of the amalgamation of these ideas was to have a lever for each cog to act like a key on a keyboard. They would all be identical and be spring-loaded for sensory feedback and a more responsive feel.

Evaluation

Overall I am happy with the end result of the project. However, it was far from perfect and there are multiple areas that can be improved on. This project was designed to challenge and strain my abilities while utilising new skills – I believe that aspect was the most successful part of the project. Despite having no prior experience with electronics, organology or woodworking, a working synthesiser was made. Building on past research while taking inspiration from Moog and Buchla – I was able to envision an idea and complete it. However, if I were to redo the project, there are multiple things that would be done differently.  Firstly, I would choose a more solid wood type as the plywood warped when it was shaped, which left gaps in the casing. Using plywood was due to budget and ease of access. Mahogany or oak would most likely be used if it were to be redone for durability and aesthetics. Another thing that would be altered would be the measurements of the panels. Because they were handmade, there are discrepancies between each panel. Ideally, it would have been done by a professional, however budget prevented this.

Due to human error, one of the cog designs was duplicated therefore the full chromatic scale was not accurate. There was again, a lack of budget to replace this cog. However, this is something that could have been easily fixed if money was no object. The cog designs themselves are extremely effective and the acrylic material is perfect for the aesthetic and durable enough to last a large amount of use. The uniform consistency of acrylic helps keep each cog perfectly similar, which keeps the tone of the instrument the same throughout the octave.

The playing surface was another area that I believe could have been done better. Due to lack of skill and materials, it was hard to build an apparatus that was effective and easy to play. The sideways play on the keys is the biggest problem as this makes playing the Tonus challenging. A sturdier design would have made the playability of the instrument much easier. Plans are in place to replace the wooden keys with acrylic ones for better support and a more robust feel.

The contact microphones were the least successful element of the Tonus. Because they have been fixed to the same panel as the motor, they pick up nothing but the motor sound. This was something I was afraid would happen. However, this is not entirely unusable. A method of recording the Tonus could include the recording from the contact mics. If one were to record the Tonus with room microphones but also take the motor sound from the contact microphones, there would be a way to cancel out the motor noise due to destructive interference. In theory, one could reverse the polarity of the contact microphone recording and add it to the room microphone recording to cancel out the motor noise.

Conclusion

At the beginning of this project, I aimed to find out whether it was possible to build a mechanical synthesizer while using previous instruments as inspiration and mathematical theory as the main foundation of the instrument. These aims have been achieved and in that regards the study has been a success. The Tonus is a playable instrument that naturally makes its tone purely from physical means. This contribution to organology is a unique physical manifestation of mathematical theory alongside unique mechanical properties. The next step may be to further apply these theories to other categories of instruments such as percussion or stringed instruments. This project has opened up a path to experiment with, create and play new apparatus. Following in the experimental footsteps of Donald Buchla Robert Moog; and transporting ideas from century-old synthesizers to the modern day has resulted in an inherently unique and special instrument. Although a prototype, the fundamental ideas are there and are ready to be built upon.

References

Apple, 2017. A Brief History of the Synthesizer. [Online]
Available at: https://documentation.apple.com/en/logicstudio/instruments/index.html#chapter=A%26section=5%26tasks=true

Barbour, J. M., 2004. Tuning and Temperament: A Historical Survey, New York: Dover Publications.

Bencic, L., 2016. Graphical Sound – from Inception up to the Masterpieces. s.l.:s.n.

Benson, D., 2008. Music: A Mathematical Offering, Aberdeen: s.n.

Bernstein, D. W., 2008. The San Francisco Tape Music Center: 1960s Counterculture and the Avant-garde. Berkeley : University of California Press.

Bijsterveld, K., 2004. Breaking into a World of Perfection: Innovation in Today’s Classical Musical Instruments. Social Studies of Science , p. 649–674 .

Brief History of Western Tuning (Understanding Equal Temperament). 2015. [Film] Directed by Nathan Nokes. s.l.: s.n.

Chadabe, J., 2001. The Electronic Century PART I: Beginnings. Electronic Musician, 1 February.

Crab, S., 2014. 120 Years of Electronic Music. [Online]
Available at: https://120years.net/the-telharmonium-thaddeus-cahill-usa-1897/

Critical Angst, 2015. MOOG VS. BUCHLA: ‘I DREAM OF WIRES’ CONTRASTS ELECTRONIC MUSIC PIONEERS WITH DIFFERING VISIONS. [Online]
Available at: http://criticalangst.com/post/127114109865/moog-vs-buchla-i-dream-of

Denton, C., 1996. The History of Musical Temperament and Pitch Before 1750. History of Music to 1750.

Dunn, D., 1992. A History of Electronic Music Pioneers, s.l.: s.n.

Fauvel, J., 2006. Music and Mathematics – From Pythagoras to Fractals, s.l.: Oxford University Press.

I Dream of Wires. 2014. [Film] Directed by Robert Fantinatto. s.l.: s.n.

Klerk, D. d., 1979. Equal Temperament. Acta Musicologica, pp. 140-150.

Liern, V., 2004. Fuzzy tuning systems:the mathematics of musicians, Valencia: s.n.

Mann, E. L., 2006. Creativity: The Essence of Mathematics, s.l.: Purdue University Press.

Marx, J., 2011. American Social Policy in the 1960’s and 1970’s. [Online]
Available at: http://socialwelfare.library.vcu.edu/war-on-poverty/american-social-policy-in-the-60s-and-70s/

Mata, A., 2013. Graphical Sound: Sound You Can See. [Online]
Available at: https://math.dartmouth.edu/archive/m5f11/public_html/proj/Mata.pdf

Merriam-Webbster , 2017. [Online]
Available at: https://www.merriam-webster.com/dictionary/synthesizer

Milne, A., 2007. Isomorphic Controllers and Dynamic Tuning: Invariant Fingering over a Tuning Continuum.

Pelletier, J.-M., 2017. Graphical sound. [Online]
Available at: http://jmpelletier.com/tag/graphical-sound/

Pinch, T., 2002. Analog Days. Massachusetts: Harvard University Press.

Ramstrum, M., 2012. HE DEVELOPMENT OF WESTERN TUNING SYSTEMS AND THE CONTEMPORARY USE OF EXTENDED JUST INTONATION, s.l.: s.n.

Rivas, T. J., 2016. The Basics of East Coast and West Coast Synthesis. [Online]
Available at: https://reverb.com/news/the-basics-of-east-coast-and-west-coast-synthesis

Ruiz, E., 2006. Music, Subjects, Creativity. [Online]
Available at: http://journals.library.mun.ca/ojs/index.php/singing/article/view/881/769

Shah, S., 2010. An Exploration of the Relationship between, Manchester: The University of Manchester.

Smirnov, A., 2011. Andrey Smirnov :: main projects. [Online]
Available at: http://asmir.info/graphical_sound.htm

The Telharmonium. 2014. [Film] Directed by Martin Cook. s.l.: s.n.

Theremin, S., 1924. United States of America, Patent No. US1661058 A.

Tkacs, K., 2010. The Serge Modular Creature: An Unauthorized User’s Manual. s.l.:s.n.

Vail, M., 2014. The Synthesizer – A Comprehensicve Guide to Understanding, Programming, Playing, and Recording the Ultimate Electronic Music Instrument. Oxford: Oxford University Press.

Weidenaar, R., 1995. Magic Music from the Telharmonium. s.l.:Scarecrow Press, INC.

White, A., 2001. New York in the 1960s. The American Prospect, 19 December.

Williston, J., 2000. Synth Museum. [Online]
Available at: http://www.synthmuseum.com/magazine/0102jw.html

Wyche, S., 2006. Historical Analysis: Using the Past to Design the Future, Berlin: Springer-Verlag Berlin Heidelberg.

Image Sources

Crab, S. (2014). The dual manual of the MkII Telharmonium. [image] Available at: https://120years.net/the-telharmonium-thaddeus-cahill-usa-1897/ [Accessed 4 Jan. 2017].

Holzer, D. (2010). Avraamov’s sound drawings. [image] Available at: http://www.umatic.nl/tonewheels_historical.html [Accessed 5 Mar. 2017].

Nokes, N. (2015). Frequencies of Pythagoras’ system and the wolf note. [image] Available at: https://www.youtube.com/watch?v=wUBkbrvCmGA [Accessed 21 Apr. 2017].

Williston, J. (2000). Telharmonium’s Tone Wheels. [image] Available at: http://www.synthmuseum.com/magazine/0102jw.html [Accessed 4 Jan. 2017].

---

[1] The ‘Tonus’ synthesizer derives its name from the Latin word for ‘tone’.