ABSTRACT

Cryptography is the science of securing data using mathematical techniques, and these are computationally intensive.

Computer information Security is a challenging issue of data communications today that touches many areas including secure communication channels, top-notch data encryption techniques and trusted a third party to maintain the database.

The general methods of encryption can only manage the information or data security. It is very easy for information to be captured by the users for malicious and evil purposes.

Therefore, there is a necessity to implement encryption and decryption methods to enhance data security. The multiple encryption techniques of present time cannot provide sufficient security; hence, it doesn’t guarantee reasonable levels of safety.

In this research paper, enhance encoding method named as ― improved cryptographic algorithm using mix column function. In this encryption technique, original data is encrypted several times with secure key bit combinations and data rehashing. This encryption technology enhances the complexity of encryption algorithms to a large extent.

Given this light, l present an implementation which employs the enhanced key bit combination,  rehashing of the cipher text and performance boost of the cache memory, which is responsible for processing the encryption and decryption modules. By implementing the key bit combination algorithm with rehashed cipher text, with proper analyses of existing cryptography algorithms. The research will include emphasis much on the functionality of performance with cache memory. After which the results will be observed and analyzed.

Keywords: mix column, encryption, security, cryptography, algorithm

CHAPTER ONE

1.1              Introduction

Cryptographic algorithms have become the most widely means of ensuring safety in regards to the defense of vital information, the protection objective known as confidentiality is the element which is taken into consideration by the hardware during the implementation and integration of the cryptographic algorithms in current communication systems (N .Singh, G .Raj, 2012).

According to Alex-Brennen (2004), cryptography is the science of encoding and decoding secret messages. The term Cryptanalysis is the study of cryptographic algorithms or resulting cipher text to evaluate the robustness and inherent weaknesses. Regularly such research is done to break an encryption algorithm or to perform key recovery. Normally, we have two types of Cryptosystems: asymmetric and symmetric key; these are both used to encrypt messages using computer algorithms that provide the users secrecy by using a cryptographic key.

The Symmetric cryptosystem uses a single key for both encrypting and decrypting of the messages. Two people using this system will share a secret key for the purpose of the encryption and decryption.

In order to transform the plain text into the cipher text and vice versa, an algorithm using a mathematical process is employed via an exchange of the key. Some know examples of symmetric cryptosystems are: Triple-DES, RC2, Data Encryption Standard (DES), RC5 Blowfish, IDEA, and RC4.

The Asymmetric cryptosystem, also called public-key cryptosystem uses two different set of keys (a public key and a private key) that works to complement each other in the process of the encryption and decryption. Among the two keys, one is used as a public key to encrypt the plain text whiles the other is kept as a secret only meant for the recipient of the message. An example SSL, is a protocol which provides communication security on the Internet. This research will however only be aimed on symmetric-key cryptosystem. The National Institute of Standards and Technology (NIST) launched a process in 1997 to select a criteria which will determine the algorithm for selecting a symmetric-key encryption that can be used for better protection of sensitive information instead of the then DES. They came to embrace a new form of algorithm which became known as the Advanced Encryption Standard (AES).

NIST declared the agreement of fifteen candidate algorithms in the same year. It asked for help from cryptographic research community to analyze these fifteen candidates. Upon completion, the analyzed preliminary results of the research got Rijndael, Twofish, RC6TM, MARS and Serpent selected for further analysis. After the analysis, NIST concluded; proposing Rijndael as the Advanced Encryption Standard (AES). Joan Daemen and Vincent Rijmen together developed Rijndae, a block cipher algorithm. McLoone and McCanny (2001) proposed the field programmable gate arrays (FPGAs), a design of Rijndael encryption which was able to utilize look-up tables to execute an entire Rijndael round function. Within that same period, (Jing et al. 2001) invented a new algorithm for computing inverse in GF (2m) on the agreed standard. (Sklavos and Koufopavlou, 2002) designed a substitute architectures and VLSI implementation designs. (Zhang et al 2002) also addressed various methods for the best utilization of hardware implementation of the AES algorithm. (Phan, 2004) examined the impossible differential cryptanalysis on the Advanced Encryption Standard up to 7 round. There was a change in the key schedule which was used to overcome the disadvantages in the block cipher system.

According to May et al., (2002), the schedule key is one main strength of the block cipher and it is concentrated on defeating any discerned weakness which may be used to attack its block system. Although the programmed key has been in existence for years now, there were various mathematical attributes and deficiencies related to its designs which were inadequate in making the block cipher system more secured. The block cipher is not focused on the concept of a key schedule. The aspect of the scheduled key has gained relatively slight notice. This was due to the fact that the block ciphers were defenseless to known attacks which was utilizing the weaknesses of their key schedules, information about the cipher key was easily deduced by attacking one or more important insights about the way the key behaves (Daemen et al., 1993; Knudsen, 1994).

Ferguson et al, (2000) did an experiment on the security of the AES candidate Rijndael and came out with some new attacks and properties of the cipher and initiated the “partial sum” technique, which substantially decreased the work factor of the devoted square attack. According to Ferguson, if you look critically at the cipher itself, the Rijndael key schedule appears to have some ad hoc design and the key schedule does not attain its stated design objectives. The 192 and 256-bit keys have a slower transmission structure than the cipher and comprises of few non-linear elements.

Likewise, (Phan, 2004) studied the attack (impossible differential cryptanalysis) on the AES up to 7 round; He added that for the attack to look computationally impossible, important attributes are often estimated. Specific elements such as bit confusion and bit diffusion help reduce the vulnerabilities of the scheduled key. According to Bauer (2007) identified confusion and diffusion as the two elements or attributes used in securing cipher text.

May et al. (2002) studied an organized and safer key schedule but there was a vast unexplored area of research regarding the bit diffusion. To conquer the deficiencies of the scheduled key, a function, Shift Row transformation is combined with the Rijndael key schedule design to diffuse the keys to strengthening the security of a block cipher. The Shift Row transformation operates on the rows of the state to provide diffusion (Savard, 2001).

Figure 1.1 Showing the Encryption and Decryption Process ( N .Singh, G .Raj, 2012)

1.2  The background of the study

Cryptography is a term used to refer to the science or art of writing in secret and has been associated with pre-historic art. The use of cryptography dates back to ancient times, approximately 1900 B.C. in Circa when Egyptian Scribes engraved non-standard hieroglyphs with an associate inscription.

Certain experts claim that cryptography might have been invented soon after writing was devised; it numerous applications found in warfare, corporate business environment and personal communication requirements among others made it most sought after. It is definitely not a shock that various forms of cryptography came into widespread when the computer communication was invented. In the period of data and broadcastings, cryptography is critical when anyone act over any untrusted medium, most importantly the internet.

There exist five primary functions of cryptography today;

1. Privacy and confidentiality: A medium used to make sure that only an intended recipients of a message could access and read that message.

2. Authentication: The procedures used to confirm if the person accessing a resource is the right authorized person.

3. Integrity: This is the assurance of that a message delivered to a person has not in any way been tempered or altered.

4. Non-repudiation: A process used to confirm that the person who sent the message was the right sender and not a fake person.

5. Key exchange: The method used to secure the exchange of crypto keys between a receiver and a sender.

In cryptography, plaintext refers to any information that is not encrypted. When the Plaintext is encrypted it is referred to as cipher text; the cipher text can successively be decrypted into usable plaintext.

The encryption and decryption are based upon some sort of cryptography scheme being used. The encryption and decryption method is usually formulated as;

C = Ek (P)

P = Dk (C)

Where P = plaintext, C = cipher text and E = the encryption methodology, D = the decryption methodology, and k = the key.

During the era of Julius Caesar, it was noted that He asked Suetonius to write his letters by exchanging D for A, and E for B and vice versa. When Augustus Octavian Caesar ascended the throne, he altered their imperial cipher system, changing C was to for A, D for B, and so on. In our technological age, we can say that he modified the key from D to C. The Arabs generalized this idea to what we call the mono alphabetic substitution, during which a keyword is chosen to change by reversing the cipher alphabet. The plaintext is written in lower case letters, whiles the cipher text is written in upper case, as illustrated in figure 1.2:

Figure 1.2 Illustrates the plaintext and cipher text (Kahn , 1996)

CRYPTOGRAPHYNMLKJIHGFEDCBA0987; however breaking ciphers of this type may be an easy pencil and paper puzzle, which can be done by an average grammar school pupil. The situation is that some letters, and a combination of letters, will be rather more common than others; for example, in English the foremost common letters area unit e, t, a, i, o, n, s, h, r, d, l, u there in order. Researchers in Artificial Intelligence (AI) showed interest in inventing programs that could resolve mono-alphabetic substitutions; exploitation letter and letter of the alphabet (letter-pair) frequencies single-handedly. They succeeded by computing 600 letters of cipher text; smarter strategies guessing the probable words can reduce this up to computing of 150 letters.

In modern times, the McEliece cryptosystem proposed in 1978 by McEliece remains unbroken and has been seen as a strong candidate for post-quantum cryptography (McEliece, 1978).  In 2007, Authors published new key agreement protocols which supported matrix conjugator search downside together with matrix logarithm function (Sakalauskas et al., 2007).

Continuing analysis in non-commuting cryptography presented new asymmetric cipher which supported matrix power function (MPF). MPF is used for key agreement protocol and asymmetric cipher construction (Sidelnikov et al., 1993). The state of the art of the perspective field of investigation was presented in a seminal book in 200x (Myasnikov et al., 2008).

3.  Statement of the problem

The 21st-century technology has evolved with many cryptographic algorithms, especially in the communication and data security arena provided to safe guide the integrity and security of data and communication in a variety of application.

Cryptographic algorithms have had particularly impact in the field of corporation and individuals and military communications and reliable security data to safe guide for transmitting.

The cipher text is used in enhancing data and communication security for individuals, corporation and military to send information such as direction, strategy, secret codes and other relevant information. An AES algorithm is dependent on the secret key; for a symmetric key encryption algorithm to be considered secure; there should be no means of decrypting the data unless you have access to the secret key (William, 2003).

According to Bruce Scheiner, it is clear and obvious that cryptography may be either strong or weak. The strength of a cryptographic structure algorithm is distinguished by the properties and also the period it will take to recover cipher text into plain text and how vulnerable it is to the attacks leveled against it. It is difficult and uneasy to decipher a strong cryptography without possession of the appropriate decoding tool.

There are numerous of encryption algorithms which can encrypt data; each encryption algorithm has its own style of formatting plain text to cipher text.

Many Cryptographic algorithms do exist, and several factors affect the selection of a particular algorithms but the most obvious is its ability to secure protected data against an attacks, as well as the Space complexity (Memory) and efficiency in doing so.

However, cryptography algorithm relies on complex mathematics computational functions that facilitate on making them slow during transaction operations. Performance such as running time, key strength, the massive memory and algorithm cannot be overlooked since that can affect the full performance and strength of the algorithm.

In order to improve the security, the key size can be increased. The method of implementing the single algorithm will have the same security issue.

The problem that exists now is to find out a cryptographic algorithm which makes use of bit keys combined, rehashing of ciper text and cache memory to enhance security in data communication.

1.4 Objectives of study

The main objective of this research is to implement an enhanced cryptographic algorithm using mix column functions. For the above objective to be met, the study will seek to address the following specific objectives:

1.    Give a detailed description of the most common symmetric key cryptographic algorithms.

2.    To implement enhance AES algorithm using mix columns to  protect electronic data

3.    To implement hash algorithm to increase the  key strength

4.    To implement AES algorithm using cache memory.

1.5 Research questions

1.    Does cryptography use 128, 192, 256-bit keys combination to enhances AES cryptography algorithm strength?

2.    Does existing AES algorithm needs enhancement?

3.    Does rehashing of cipher text enhance AES algorithm security?

4.    Does cache memory enhance AES algorithm?

1.6  Research hypothesis

In line with above research questions, the following research hypothesis was formulated.

If the functionality of combining the key bits, cache memory, rehashing of data and encryption and decryption time are implemented, the efficiency, strength and performance will be improved on the cryptographic algorithm.

1.7 Significance of the study

This research endeavour to promote and enhance effective AES cryptographic mechanism of data and communication security. This research will be beneficial to researchers and users in aspects of communication and computer security.

Moreover, this research will be helpful in implementing a useful algorithm to enhance communication, and this research will educate cryptographers in deciding best suited cryptographic algorithm implementation for the enhancement of AES cryptographic security.

1.8 Organization of the research

Chapter 1 reveals the introduction; highlighting the background of the study, the problem statement, objectives, and significance of the research, the research questions and the research hypothesis.

Chapter 2 presents the review of the literature, related research and the problem

Chapter 3 explains the methodology used in carrying out this research. It looks at the research strategy used thus the research approach used in gathering the data. The implementation of the idea is also broken down and explained here. This includes the technologies used and how they were merged to develop the application.

Chapter 4 gives an in depth analysis of the experiments which was carried out in order to prove the hypothesis and the main findings that were derived. The observations on the main findings were then analyzed.

Chapter 5 gives a summary of the whole research including the limitations, future suggestion on the work, and an overview of the general discussion about the research.

CHAPTER TWO

LITERATURE REVIEW

2.1  Introduction

This chapter deals with the definitions of some concepts used in this study. It also outlines theories and literature which forms the basis of the research. It also proceed to give an account of some of the current research efforts directed toward the problem at hand.

The literature focuses the attention towards elaborating on details of various existing cryptographic algorithms, theoretical emphasis on the cache memory, key bit strength and rehashing of cipher text.

The implementation practicability in large scale integration atmosphere was additionally studied and analysed wholly (A.J. Elbirt, et al., 2001). The expanse of telecommunication (internet and wireless communication) has brought about an increase in the demand for security measures and devices that can safeguard a users’ information transmitted over electronic medium (the internet, phone communication). Two types of cryptographic systems have been developed for that purpose; bilaterally symmetrical (secret key) and uneven or asymmetrical (public key) cryptosystems (N. Singh, et al., 2012).

Bilaterally symmetrical cryptography includes Data Encryption Standard (DES), and Advance Encryption Standard (AES); with this form of encryption, the sender and receiver use a single key for encoding and decoding. An example of the asymmetric algorithm is Rivest-Shamir-Adleman (RSA), this type of cryptography uses two separate keys, one for encryption known as the public key and another which is a secret key for the decryption or decoding of the message.

Bilaterally symmetrical cryptography is best appropriate for the encoding of a large amount of data. The rule outlined by the National Institute of Standards and Technology (NIST) of the US has been accepted widely to interchange DES as the new bilaterally symmetrical encoding rule.

2.2 Types of encryption algorithm

Key-based encryption algorithm can be classified into two types; the regular symmetric algorithm also known as secret key algorithm and the asymmetric algorithm also known as public key algorithm. The difference between this two is that, the symmetric algorithm uses the same key for both encryption and decryption whereas the asymmetric algorithm uses two different set of keys, one for encryption and the other for decryption thus one can never decrypt and encrypted message using the decryption key  (decryption.com, 2017)

2.2.1 Symmetric encryption algorithms

Symmetric encryption algorithms is classified into two types depending on how it encrypts the plain text. When the plain text is encrypted one bit at a time, it is known as stream cipher encryption but when the plan text is encrypted in more than one bytes at a time (taking more bits at time) it is known as block cipher encryption. It can normally takes 64 bits at a time and encrypt then as a single unit (decryption.com, 2017)

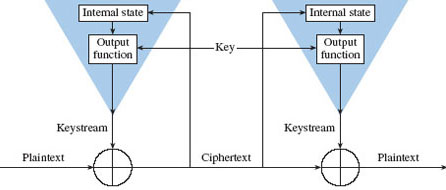
Figure 2.13 Self-synchronizing stream cipher (Source: Schneier, 1996)

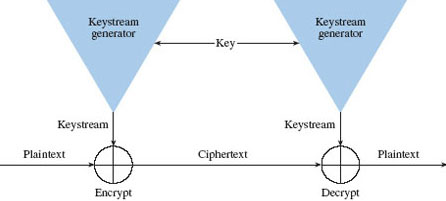
Figure 2.15 Synchronous stream cipher (Source: Schneier, 1996)

2.2.2.1 Steam and Block ciphers

The steam cipher takes in one bit or byte at a time and turns it into a cipher text using an infinite steam of pseudorandom bits as key. In order to make it impenetrable, the key must never be reused; moreover, the pseudorandom generator should be in such a way that it could never be predicted. When stream cipher is approximated to an idealized cipher it is known as a one-time pad. This one-time pad must be able to employ random key in order to achieve “perfect secrecy” to prevent brute force attacks. One issue which the one-time pad encounters is that it key should be longer than the plaintext; that is you need more than three times the size of a file to be able to idealize the one-time pad. This makes the implementation of the steam cipher not idealized for day to day public use unless if its key is reduced to less than the plain text which can be strong but not recommended for matters of national security (Villanueva, 2015).

The block cipher encryption algorithm on the other hand encrypts n-bits of data called the block at a single interval. The interval for the blocks are 64 bits, 128 bits, and 256 bits. For instance, a 128 bit block will take in 128 bits of plain text and encrypt it into 128 bits of cipher text. When the bits of plain text becomes smaller than the block size, padding schemes are introduced. Today, more of the symmetric ciphers used are actually block ciphers. Examples are Triple DES, Blowfish, AES (Villanueva, 2015).

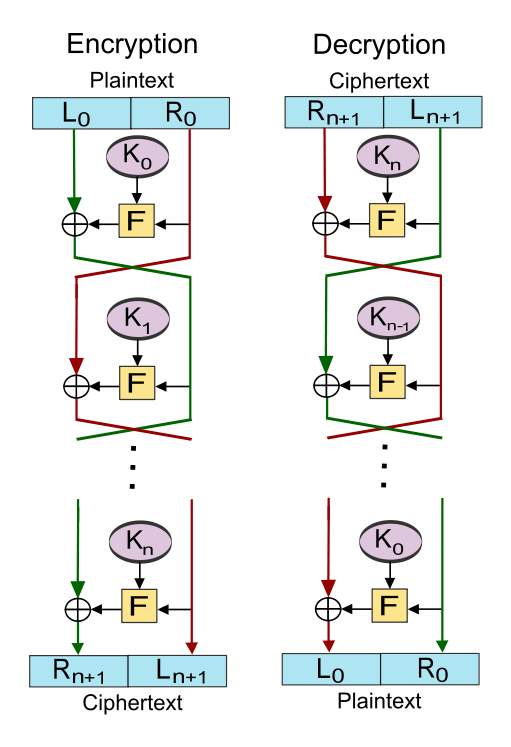
Figure 2.1 Feistel cipher (Springer-Verlag, 1996)

Symmetric block ciphers are mostly based on Feistel Cipher structure as shown in Figure 2.12. It combines parts of substitution, permutation also known as transposition, and key expansion; these produces a completely obscure statistical properties of the original message referred to by Claude Shannon as confusion and diffusion. Diffusion dissipates statistical structure of plain text over the whole cipher text whiles confusion makes the relationship between the key and the cipher text very complex (Stallings, 2017).

Block ciphers operate in several modes; the following are the most significant:

         Electronic Codebook encrypt each block independently. Here all similar plain texts are encrypted in the same way. There are no chaining and error propagation in this mode. It does not hide the patterns in the data and therefore is improper for long messages. It is also vulnerable to replay attacks

         Cipher-Block-Chaining mode develops a reaction component which is attributed to a coding plan and prevents against deletion, and insertion attacks, brute-force, a one-bit error in the cipher text will result in error propagation which can yield to an entire block error within the decrypted plaintext block

         Cipher Feedback mode uses similar messages and chaining like the Cipher Block Chaining mode. It allows plain text to be encoded in groups lower than the block extent; and might help in some propositions like encoding fatal input. Using this mode allows every letter to be stored in the register. Its key is based upon the previous cipher text.

         Output Feedback mode makes preprocessing possible. It prevent the whole plainttext from developing the same types of cipher message blocks. It does not allow random access or parallelization. In Output Feedback, a single-bit error in cipher text may only affect the corresponding plain text. Similar to Cipher Feedback and Output Feedback, Counter mode operates on the blocks. There are no error propagation.

2.2.2.2 Blowfish encryption algorithm

Blowfish was designed by Bruce Schneier in 1993 as an alternative symmetric encryption algorithm to the already existing ones. It has a size of 64 bits; it key length varies from 32 bit to 448 bits. It uses massive key depended S-boxes and is a 16-round Feistel cipher. During its key scheduling, it does several encryptions producing large pseudo-random lookup tables. This pseudo-random lookup tables is dependent on the key the user supplies in a complicated way. Due to this, it can prevent extreme intrusion such as linear cryptanalysis and linear cryptanalysis.

This procedures has been proven to be very resistant against differential and linear cryptanalysis. Regrettably, because of its massive use of memory space, it is not ideal for environment smaller organizations who do not have the memory power. It is identical to the structure of CAST-128 (S-boxes). Blowfish is becoming recognized since it is fast and free. It only known is successful attack is when one uses a key which is weak (encryptionanddecryption.com, 2017).

.2.2.2.3 CAST

Cryptographers called Carlisle Adams and Stafford Tavares invented CAST and name it after their initials (C.A.S.T). CAST is a normal 64-bit Fiestel block cipher. Its 128-bit (CAST-128) is DES-like SP Network (a series of linked mathematical operations) used in block cipher algorithms cryptosystem which is part of the Feistel shape and exploits eight mounted S-boxes.

CAST-128 supports different key lengths between 40 and 128 bits and can prevent again both linear and differential cryptanalysis. There is also no known way of penetrating CAST using brute force attack. CAST is currently the standard cipher in PGP  (encryptionanddecryption.com, 2017).

2.2.2.4 Data Encryption Standard (DES)

The Data Encryption Standard (DES) is a 64 bit size symmetric block cipher which uses a 56 bit key to encrypt and decrypt data. It was embraced as the federal standard for use in the United States in 1977.

It uses permutations and substitutions in its algorithm and often operates on blocks of equal size. In order for it to encrypt into the cipher text, the DES algorithm is repeated continuously for 16 times. In order to brute force attack the algorithm to find the key, the number of rounds required is exponentially proportional to the time needed and therefore as the number of rounds escalates, the security of its algorithm also increase.

The DES cipher text data has been safe for many years because in the past only handful of institution had the processing power to crack it; however a team of cryptographers were able to crack it in 3 days in July 1998. In 1999, ten thousand computer networked PCs were able to crack the DES cipher text in less than a day making it susceptible to attacks. The Triple DES then became the stronger preferred standard.

The Triple DES algorithm uses Three times that of DES and it uses an alternative key for at least of its phases which offers it a collective key size of 112 to 168 bits. Its expected strength defeats brute force attacks using key of approximately 112 bits but it is slow compared to newer types of block ciphers; it can therefore not be used in long term solution. NIST in 1997 replaced DES entirely with Advanced Encryption Standard (AES) (encryptionanddecryption.com, 2017).

2.2.2.5 IDEA encryption algorithm

International Data Encryption Algorithm (IDEA) is a type of symmetric encrytion algorithm which was invented by Professor J. Massey and Dr. X. Lai to take over then then DES. Compared to DES 64-bit key, IDEA uses a 128 bit size key which makes it impossible to break using brute force attack. It was one of the prefered known algorithm which has been used for years with no susccesful susceptible attacks attributed to it.  It can prevent both linear and differential analysis (encryptionanddecryption.com, 2017).

2.2.2.6 SEED

Korea Information Security Agency (KISA) developed SEED, a Feistel network which employs 16-round with 128 bit key offering 128 bit size blocks to oust the then 40-bit encryption algorithm because of its weaknesses. SEED is not susceptible to both differential and linear cryptanalysis; even to linked key attacks. Although it comprise of a G-function operating on 32-bit halves, it is implement on Feistel F-function using 64-bit halves. It was approved by ISO/IEC as a standard (encryptionanddecryption.com, 2017).

2.2.2.7 Tiny Encryption Algorithm (TEA)

TEA which stands for Tiny Encryption Algorithm is a block cipher cryptography famously known by how simple it is to implement by just using a few lines of code. It was developed by David Wheeler and Roger Needham. It structure is a Feistel; it adopts 64 rounds constrained in cycles of termed pairs. TEA has a couple of issues which is the more you iterate it the more secure it becomes but also the slower it becomes. This make it inadequate for use in Cryptographic hash function ((Bruce Schneier, et al., 1996). Tea is also susceptible to some related key attacks because it needs 223 plain texts below its key combination with 232 time complexity and thus XTEA cipher is mostly used (Steil, M., 2005).

Figure 2.2:  Tiny Encryption Algorithm  ( Hernández et al , 2002)

2.2.3.8 Triple DES

Triple Data Encryption Algorithm  (3DES/TDEA/Triple DEA) is a symmetric block cipher encryption algorithm which takes the Data Encryption Algorithm and writes all the blocks three times thus the name 3DES. It helps in protecting the key against attacks (United States Department of Commerce, 2005).

 

2.3 Classification of encryption

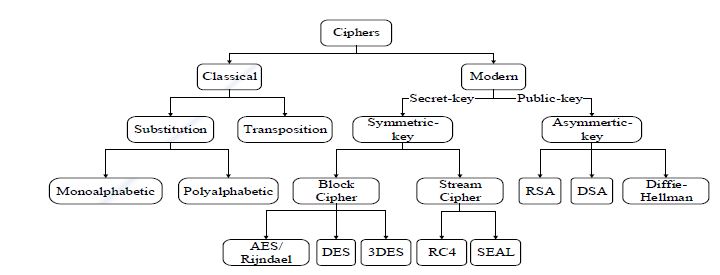
Figure 2.3 Classification of Encryption Methods (Source: Hamdan.O.Alanazi et al, 2010)

2.4 Comparison of RSA, DES, 3DES and AES

The table below portray the comparison between Asymmetric and symmetric. It can be noted that examples of the Asymmetric algorithm is slower than the Symmetric Algorithms.

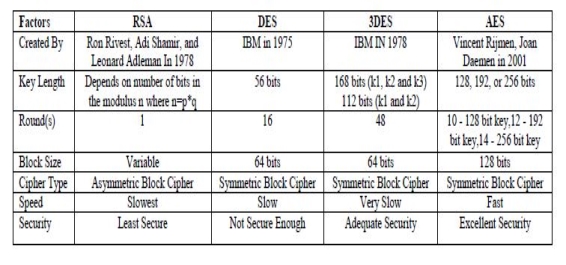
Figure 2.4 Comparison of cryptographic algorithms (Source: Aman Kumar, 2012)

2.5 AES cryptographic algorithm

Advanced Encryption Standard (AES) Cryptographic algorithm is classified as a symmetric encryption algorithm. It was chosen by the National Institutre of Standards and Technology as the standard which replaced the Data Encryption Standard (DES). The main advantage of AES over DES as given by National Institute of Standards and Technology was for its efficient key setup time and also its low memory utilization; moreover, it was chosen because its operation was straight forward and was able to prevent against timing and power intrustions. This made it perform well in various environments (encryptionanddecryption.com, 2017).

AES was invented by Vincent Rijmen and Joan Daemen so it was original called Rijndael using the last two surmames from its creators. AES is excellent in encryption and decryption and was therefore chosen by NIST as a standard federal information processing algorithm. It uses 128, 192 or 256 bit key size for encryption. All the three set of key sizes portrays different behavior in the cipher text. The stronger the key size, the more complex and secured its cipher text becomes (encryptionanddecryption.com, 2017).

The illustration below briefly describe the transformation:

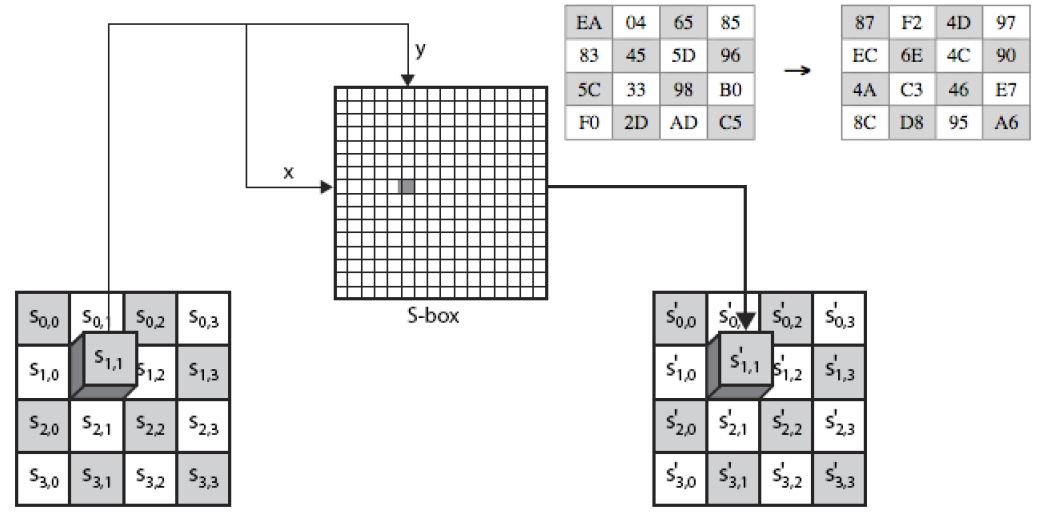
2.5.1 Substitute Bytes

The Substitute Bytes is also known as Sub Bytes. This serves as a normal table which uses an S-Box containing 16 by 16 bytes of matrix values. The permutation of the S-Box is not random but has a structured method for the tables. It contains the possibilities of all 8 bits. The S-Box is risk-averse to attacks of cryptanalysis.  (Jie Cui, et al., 2011).

Figure 2. 5 AES Substitute Bytes Illustration (Jie Cui, et al., 2011)

2.5.2 Shift Rows Transformation

Shift Row is a simple permutation of stages. The following illustrates those stages:

Stage 1.

The state of row one is not altered.

Stage 2.

In a circular way, row two is pushed to the left by one byte.

Stage 3.

In the same circular way, row three is pushed again to the left by two bytes.

Stage 4.

Another circular shift to the left by 3 bytes is applied to row four.

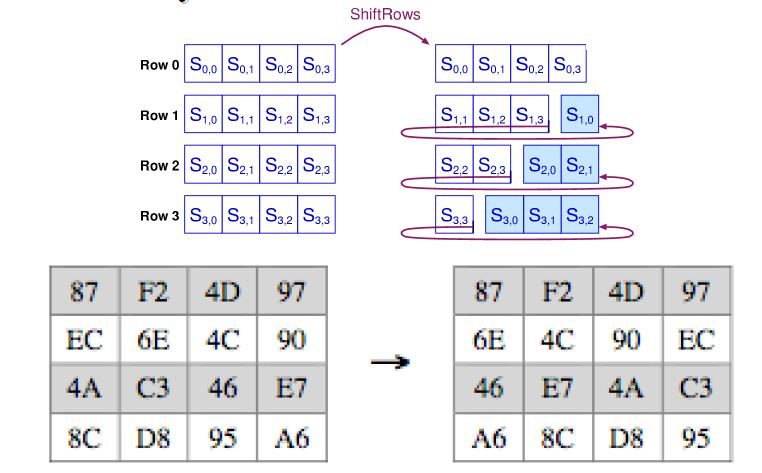
Figure 2.6 AES Shift Row Illustration (CSE, 2011)

From the illustration above Figure 2.6, you can ascertain that data on the first row has not been altered in any way; moving down to the second row, a byte of that has been shifted in a circular way to the left. From here down to the fourth row, the change in byte increases by one all to the left in a circular way. (AES FIPS PUB 197, 2001). A graphical representation of shift rows transformation a shown in figure 2.7

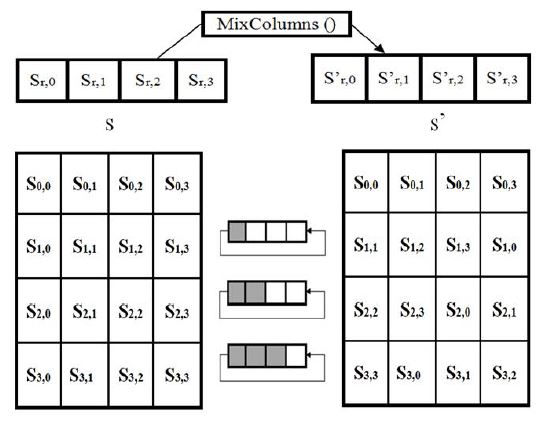
Figure 2.7 Shift Rows Transformation (NIST, 2001).

 

2.5.3 Mix Column Transformation

Mix Column Transformation is an arithmetic substitution of the type GF (2⁸) where each operation is done on the column itself. Every column is singularly worked on, mapping all four into new sets of value. The values of every single product matrix becomes the addition of the product in row one and its equivalent column thus performing them in the GF (2⁸).

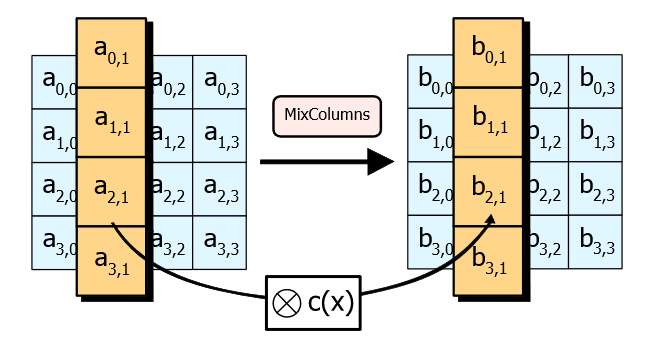
Figure 100 Krishna Sundarram (2015).

2.5.4 Add Round Key Transformation

The Add Round Key merges the sub key with its state. In all the series of steps, the AES key schedule generates a sub key which has the same size as from its parent state. The XORed is used in merging the states bytes with its sub key. (NIST, 2001).

2.5.5 MixColumns Decryption Procedure

In other to decrypt the cipher text of the AES. The transformation of each procedure is reversed: InverseSubstituteBytes, InverseShiftRows, InverseMixColumns, AddRoundKey (NIST, 2001)

.

2.8 Hash Functions:

Hash Functions are sets of functions which can link irrational data to a fixed size of data. The results from it are called hash values or just hashes. Hash functions are helpful in cryptography: one main example of its implementation is the hash table used for looking for data stored in tables in many applications in computer science. (Bruce Schneier, 2016).

There are five main components in hash function

1. Similar data from different sources will always produce the same hash values.

2. It is always quick to figure out the hash value for any messages.

3. Creating data from hashes is futile.

4. The hash value will change with the least alteration of a message.

5. Divergent messages can never be achieved from same hash value.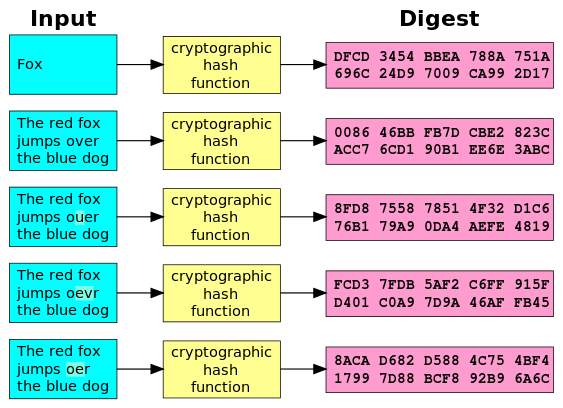

Figure 2.12 Demonstrates a Hash Function (SHA-1) Implementation Cryptographic (Source: Wikipedia).

2.12  Description of Memory Encryption

The memory address scrambling is the mapping of consistent locations of collected information to physical areas on the chip given by memory administration units, address encryption and memory format. It is expected as a counter measure to data spillage of the areas of stored information in the memory brought on by successive access to memory addresses, which is extremely normal in practical applications. Preferably, an address encryption ought to appropriate the intelligent addresses consistently over the entire memory address space while changing them into physical locations. In fact, information with successive sensible locations ought not be composed to consecutive physical addresses and be free of the block length of the fundamental block figure. This can be checked by gauging the relationship between the sensible and physical addresses (X. Zhuanget et al, 2004).

In the writing, there are diverse strategies to perform memory encryption, for example, in part or completely scrambling of the memory addresses. In the previous technique, just the addresses inside the most recently got to blocks of the memory are encoded. In the last approach, the entire consistent address space is encoded at cost of extra inactivity and power utilization. Beneath table incorporates the address encryption plans accessible in the literature and remarks with respect to their efficiency. Note that the referenced writing does not infer any suggestion for the utilization of these strategies (X. Zhuang et al, 2014).

2.13  Modes of Operation for Memory Encryption

The block ciphers of the  encryption takes care of data encrypt in n-bit blocks,  needs to use a mode of operation to carry out  encrypt data which exceeds the size of n bits. System memory encryption systems are generally considered, mostly address information is utilized as a formed of the mode of operation. The table as illustrated in figure 2.15 consist a compilation of modes of activity suitable for memory encryption simultaneously with key points of the modes. Nevertheless, the security on the mode of operation mostly relies on the main idea that the elemental block cipher is cryptographically secure.

The illustrated manner of operation make use of the idea of fine tune block ciphers proposed by (M. Liskov et al,2002) .The authors claim that using fine tune block ciphers enables acquiring different encryption functions without making changes to the encryption key, which is usually an indeed costly process, but changing the tweak instead. Fine tune block ciphers, a pseudo random tweak value is usually computed and used as a third input to the encryption function. Here, the idea of including a fine tune is to have variability on cipher texts that corresponds to the same plaintext when different fine tune are used. Although the use of a fine tune does not provide additional security to the emphasizing block cipher, the variability comes great in most cryptographic applications such as memory encryption. In the figure 2.16 as illustrated modes below, the fine tune is computed by encrypting the page information, which is a unique identifier for a collection of data blocks, using the underlying block cipher with an encryption key. This means, each encryption page has unique encryption function making it even harder to attack the system using selective plaintexts or chosen cipher texts which are located at different pages. The referenced literature does not suggest any remedy for the use of operational modes.

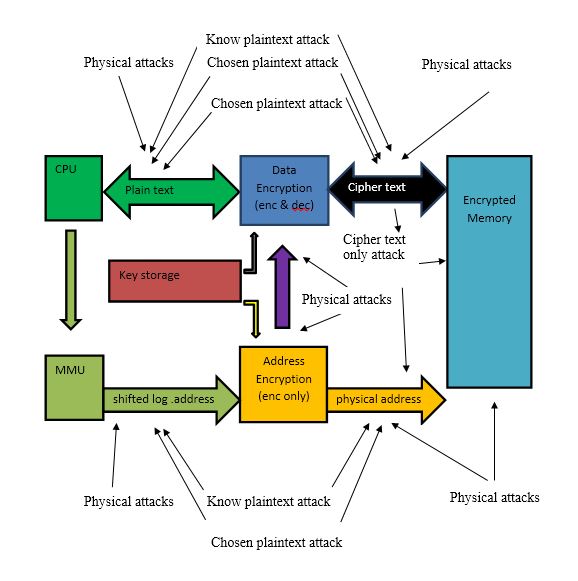
Figure 2.16 Illustrates Memory Attack Scenarios (M. Liskov et al, 2002)

Passive physical attack could be carry out bypass the encryption including but are not limited to the following:

1.                Plaintext addresses reading from the address bus segments between the CPU and the MMU or between the MMU and the address encryption module during reading or writing the data under attack bypasses the address encryption.

2.  Plaintext reading of data from the plaintext data bus segment during reading or writing the data under attack circumventing the data encryption. This bypass of data encryption reads plaintext blocks in the sequence they are used by the CPU. This information may be sufficient for reconstruction of the logical addresses and therefore bypass the address encryption as well.

3.  Plaintext data reading of the plaintext data bus segment and the plaintext addresses on the bus segments during reading or writing the data under attack bypasses the memory encryption.

4. Reading of the data encryption decryption key part from the key storage, reading the addresses from the plaintext address bus segments, and reading the cipher text with their physical addresses by passing the memory encryption.

5. Reading of the data decryption key part and the address encryption key components from key storage, and reading the cipher text with their physical addresses circumventing the memory encryption.

CHAPTER 3

METHODOLOGIES

3.1 Introduction

The relevant methods and procedures used to achieve the purpose of this research is classified as the methodology. The main purpose of this observation and experiment includes accounting for the extensive discussions that encompass the theories summing up Asymmetric and Symmetric Cryptographic algorithms. The research however focus more on how to make a more efficient and faster implementation of mix columns algorithms.

3.2  Research strategy

The motive of the research is to prove the hypothesis that enhanced mix column AES perform faster with improve bit key length, cache memory and rehashing of cipher text than most encryption cryptographic algorithms. This research will be carried out by the running implemented existing cryptographic algorithms. The outcome will be observed and analyzed. The algorithm will be on the most prevailing computer systems in the laboratory which makes efficient use of programming languages like JavaScript, HTML, jQuery and ATOM.

Which type of research design is best for this project?

Some research designs have been sighted. According to Yen (2003), research emerge in several forms; Case Study, Experiments, Survey, etc. The best choices for selecting any of the forms is dependent on the type of research being conducted. For instance, case study research makes us comprehend complex circumstances. It might also be used for the addition of strength or the extension of experience to what existed in the past. Case study research has brought us the understanding of a complicated situations or object and can be used to extend experience or add strength to what is already exist through the previous study. Case studies establishes differences among comprehensive contextual studies of events or conditions and their relationships.

Most Researchers have used the case study method for several years within various fields. Social scientists for instance have made an extensive utilization of qualitative research method to examine contemporary real life circumstances and have provided the basis for the application of ideas and extensions of methods. Researcher Robert K. defines the case study research method as an empirical inquiry that investigates a contemporary phenomenon within its real life context.

When the lines between phenomenon and context give an unclearly evident; then the multiple sources of evidence are used (Yin, 1984, p.23).

Research designs which is merged with Survey research-based procedures have fail to address the main motives for researches dealing with laboratory experiments on computers that find the correlation between two object and variables; therefore the research strategy that will be adopted and will be suitable to implement the empirical research is an experimental research.  The experimental research is a practical method that arbitrate between competing models or hypotheses (Cooperstock, 2009). Experimentation can also be used to test theories or new hypotheses which are in existence to support them or disprove them (Akash Kumar Mandal et al., 2012). An experiment is a step by step procedure carried out with the intention of confirming, refuting or proving the validity of a hypothesis. The experimental research usually points at examining present or upcoming hypothesis, which is an anticipation of how a particular process or phenomenon operates. If the test is correctly and accurately carried out, the outcome will either support or disprove the hypothesis. Experimental research is a very primary component of the engineering and scientific method. The root of an experimental study is the hypothesis.

3.3  Research approach

The research is based mainly on a quantitative approach. Denzin and Lincoln (1994:2) asserts that qualitative research addresses the study of things in their original or natural contexts by attempting to interpret their outstanding traits. Quantitative research can be used in the natural sciences like physics for studying natural happenings, for techniques like mathematical modelling, and experiments in the laboratory. Although quantitative research is often employed in survey techniques within social settings, it can be used in context with qualitative methods (Myers, 1997).

Quantitative methods underline objective measurements, analytical and numerical interpretation of data obtained from surveys or managing pre-existing statistical data using computational approaches. The quantitative analysis concentrates on data gathering from a cross section of people or to elaborate on a particular phenomenon.

3.4  Data collection: Experiment and Observation

As noted above, this research method is a quantitative one and using Experimental research strategy. The research will be carried out on a computer system with certain specifications which are fully optimized.

This research will be conducted on “Lenovo” which is fully optimized; Intel i7 (Skylarked 6th Generation) CPU with 2.6 GHz Speed, 16 gigs DDR4 RAM and AMD Radeon R9 M375. According to the research strategies, Cryptographic algorithms will be run on these Processors to prove a hypothesis which states the strength and performance of security of encryption algorithm depending directly on it.  Data will then be collected for further analysis to validate the hypothesis. Some Data collection techniques exist, such as Sampling, Questionnaires, simulation, Observatory, etc.

Boyd and Westfall (Boyd et al., 1989) have defined experimentation as a research method in which, one or more variables are manipulated under conditions that permit the collection of data that show the effects, if any, of such variables in an unconfused fashion. Collecting data by experimentation is done in such a manner as to permit relatively unambiguous interpretation. In the realm of the sciences, experiments determine and prove cause-and-effect relations.

3.5 Framework for data analysis

This research is highly dependent on the test conducted on a computer with a highly optimized feature; Intel i7 CPU with speed 2.67GHz. At the end of the test, the expected outcome should prove the following; mix column encryption using 128,192 and 256-bit keys combined and rehashing of data should improve the strength as against the current trends of computer security hacking, and CPU optimization due to cache memory usage.

A significant portion of this research is to examine the data collected from the experiment conducted, comparing and contrasting results obtained from the strength of encryption, and to reflect on the results on the findings in the literature review.

The tool to be used to critically and statistically analyze the data obtained will be Angular JS and JavaScript by using the Atom interface in parallel computing toolbox. This IDE interface is powerful to enable a finer – grained control to fasten portions of code that were performance bottlenecks.

As defined by (Aliaga et al, 2000), Quantitative research is “explaining phenomena by collecting numerical data that are analyzed using mathematically based methods.

3.6  EXPERIMENTAL EQUIPMENT / TOOLS

The computer used for this research must meet the following specification basic specification:

OS: Microsoft Vista SP1/Windows 7 Professional / 8 /10.

•                                                                    Processor Speed: 2.6 GHz Intel Pentium IV or equivalent
•                                                                    Memory space: 2 GB
•                                                                    Disk space: 1 GB of free disk space

OS: Ubuntu 11.04 and above

•                                                                    Processor Speed: 2.6 GHz Intel Pentium IV or equivalent
•                                                                    Memory space: 2 GB
•                                                                    Disk capacity: 850 MB of free disk space

OS:  Solaris OS version 11 Express (SPARC)

•                                                                    Processor Speed: UltraSPARC IIIi 1 GHz
•                                                                    Memory space: 2 GB
•                                                                    Disk space: 850 MB of independent disk space

OS:  Solaris OS v11 Express (x86/x64 platform edition)

•                                                                    Processor Speed: AMD Opteron 1200 Series 2.8 GHz
•                                                                    Memory: 2 GB
•                                                                    Disk space: 850 MB of free disk space

OS:Macintosh OS X 10.6 Intel

•                                                                    Processor: Dual-Core Intel (32 or 64-bit)
•                                                                    Memory: 2 GB
•                                                                    Hard Disk capacity: 850 MB of free disk space

3.7  Implementation

This project implementation happens to be last development which involves the conversion of the system specification into execution. Which includes the system design and implementation and evolutionary approach to development are employed, it may also include refinement of the system specification (Dustin, Elfriede, 2002). It involves the physical display of how the system works and runs. It also covers areas such as the phases of programming, system testing, and posts implementation evaluation.

3.7.1 Mix column implementations using AES

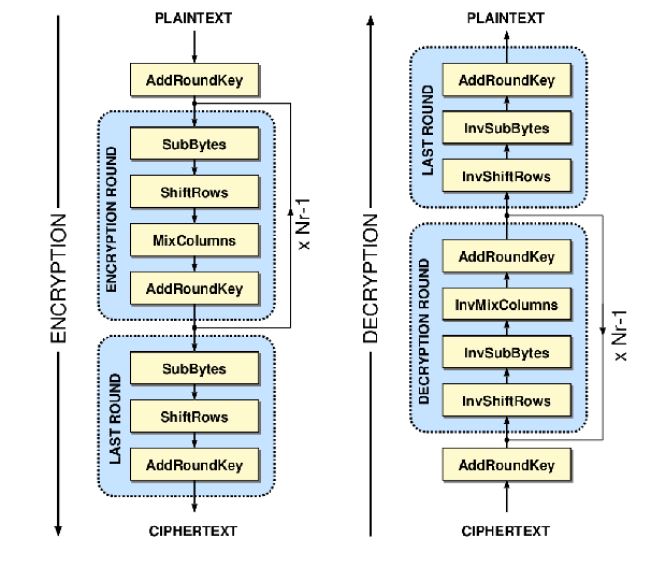
Figure 3.1 AES basic structure of the AES algorithm: encryption (left), decryption (right) (Source:iis-people.ee.ethz.ch).

AES algorithm is a FIPS (Federal Information Processing Standard) standard and is a symmetric key within the sender and recipient uses a key for encryption and decryption (N .Singh, et al, 2012). The block length is fixed to be 128 bits (Nb = four words). Meanwhile, the block length of the cipher key can also have 128 or 192 or 256 bits, and this can be interpreted by Nk = four (4), six (6), or eight (8) words respectively.

The AES algorithm is an iterative algorithm. The iterations are known as rounds, and the entire number of rounds; Nr is 10, 12, or 14, when the key lengths are 128, 192, or 256 bits, respectively. The 128-bit plaintext block is broken down into 16 bytes. These 16 bytes are arranged or grouped into a 4 x 4 array known as the state. The entire execution of all the inner operation of the AES algorithm is implemented in the Formal. Each byte in the State is shown as an element of Galois Fields, GF (2^8).

The irreducible polynomial is used in the AES method to form the Galois Field (2^8) field which is m (y) = 8y+ 4y+ 3y + y +1y. (1)

In figure 3.1, each round except for the final round consists of four transformations: the Extra Bytes, the Modification Rows, the Mix Column, and the Add Overweight Key (AOK), while the last round has no mix column () transformation.

3.7.2 ALGORITHM BLOCKS

The AES algorithm can be classified into three blocks.

3.7.2.1 Initial Round:

The initial round is the first and simplest of the stages; it only counts one operation: Add Round Key.

Remark: The inverse of this operation block it is self.

3.7.2.2 N Rounds:

N being the number of iterations. This variety varies in keeping with the scale of the key used. (128 bits equal to N=9, 192 bits equal to N=11 and 256 bits equal to N =13). This second stage constituted the N iterations together with the following four operations. The operations are as follows;

             

 3.7.2.3 Final Round:

This stage is sort of identical for one in every of the N iterations of the second stage. The sole distinction is that it does not embrace the operation mix columns

3.7.3 Add round -key

A process of a humble bitwise XOR equivalent to the whole Galois Fields combines the key that is overweight to the National. The two towers keys comprises of  4 arguments the procedure of the key agenda.

Figure 3.2 Show the Implementation of the AES Add Round – Key Block

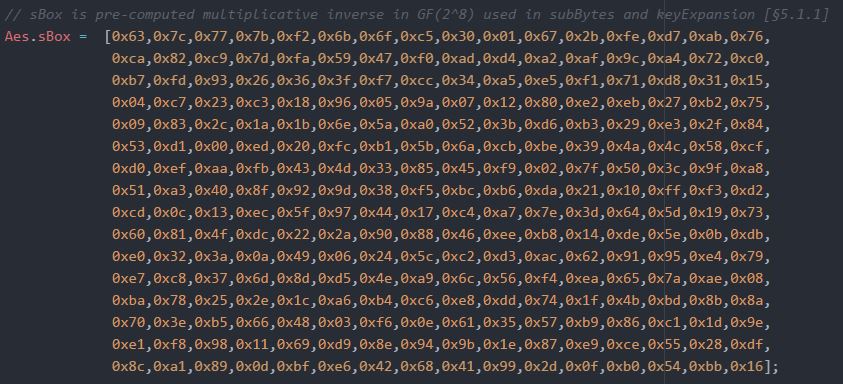
3.7.4 SubBytes

In SubByte a non-direct byte substitution that works autonomously on every byte of the State utilizing a substitution table called the substitute-box. To build this S-box, which is reversible, by forming two changes:

Catering for the multiplicative opposite in the determinate field GF (2^8) with (x) = x8 + x4 + x3 + x + 1(1)

Using the irreducible polynomial; the element {00} is mapped onto itself.

Figure 3.3 Sub-Byte Block

3.7.5  Shift Rows

Remark: The operation of the inverse function of this Inverse shift row consists of substituting the left shift with the right shift.

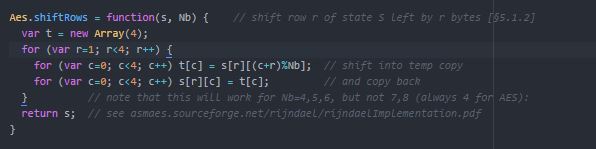
Figure 3.4 Show the implementations of the Shift Keys

3.7.6 Mix Column

The mix column functions on the State column to column, giving every column as per the polynomial over GF (2^8). These polynomials are increased by (x4 + 1) with a set binomial a(x), specified within the standard.

3.7.6.1 Mix Columns theory

The mix columns theory is calculated using this formula (FIPS 197, 2001) below;

r0r1r2r3=  2311123111233112a0a1a2a3

Where r0, r1, r2 and r3 happened to be the results after the transformation. a0 – a3 may be acquired from the matrix after the information goes through replacement process in the replacement Boxes. I will now emphasis on discuss the column transformation.

I will elaborate with this example:

d4bf5d30=  02030101010203010101020303010102= 046681e5

In this explanation  a0 – a3 is equal to d4 – 30 and r0 – r3 is equal to 04 – e5. One aspect to consider is the fact that it still follows the matrix multiplication rules: row x column. The matrix size resembles this:

[4 x 1]. [4 x 4] ≠ [4 x 1]

Understanding AES Mix-Columns Transformation Calculation a0 – a3 r0 – r3. To obtain [4 x 1], the formula needs to be [4 x4]. [4 x 1] = [4 x 1]

Therefore l have to switch matrices over.

02030101010203010101020303010102. d4bf5d30=046681e5

Now l have to calculate the subsequence solutions, as mention early, the rows with the columns are multiplied. l will multiply the rows with the column. The first row of the first matrix is taken and multiply them with a’s values.

The formula below is used to get the r0 value;

r0 = {02.d4} + {03.bf} + {01.5d} + {01.30}

Will extend into the steps one at a time. 1. {02.d4}.

d4 = 1101 0100

3.7.6.1 AES Mix Columns Transformation Calculation

{d4}. {02} = 1101 0100 << 1 (<< represents the shift to the left, 1 represents the total number of shift made, 0s represent the pad)

= 1010 1000 XOR 0001 1011 (because the leftmost is a 1 before shift)

= 1011 0011.

1010 1000 and 0001 1011 (XOR) equals to 1011 0011

Now l implement the same for the next set of values, {03.bf} as l convert bf into binary:

bf = 1011 1111

In this case, l am multiplying 03 to bf. Just multiply them directly. For my case, I followed what was suggested in the book (William Stalling, 2006), l split 03 up in its binary form.

03 = 11 therefore = 10 XOR 01

And now able to calculate the result.

{03}. {bf} = {10 XOR 01}. {1011 1111}

= {1011 1111. 10} XOR {1011 1111. 01}

= {1011 1111. 10} XOR {1011 1111}

= {1011 1111} x 1[in decimal] = 1011 1111

= 0111 1110 XOR 0001 1011 XOR 1011 1111 equal to 1101 1010

{01.5d} and {01.30} is basically multiplying 5d and 30 with 1(in decimal) which we end up with the original values. There is not a need to calculate them using the above method. But we do need to convert them to binary form.

5d = 0101 1101

30 = 0011 0000

Now, l can possibly add them together. As they are in binary form, with XOR using addition.

r0 = {02.d4} + {03.bf} + {01.5d} + {01.30}

= 1011 0011 XOR 1101 1010 XOR 0101 1101 XOR 0011 0000

= 0000 0100

= 04 (in Hex)

Will emphasis on the next row.

02030101010203010101020303010102. d4bf5d30=046681e5

r1 = {01.d4} + {02.bf} + {03.5d} + {01.30}

1. {02.bf}

{bf} . {02} = 1011 1111 << 1

= 0111 1110 XOR 0001 1011

= 0110 0101

2. {03.5d}

{5d}. {03} = {0101 1101. 02} XOR {0101 1101}

= 1011 1010 XOR 0101 1101

= 1110 0111

Therefore,

r1 = {01.d4} and {02.bf} and {03.5d} and {01.30}

= 1101 0100 XOR 0110 0101 XOR 1110 0111 XOR 0011 0000

= 0110 0110 therefore equal to 66 (in Hex)

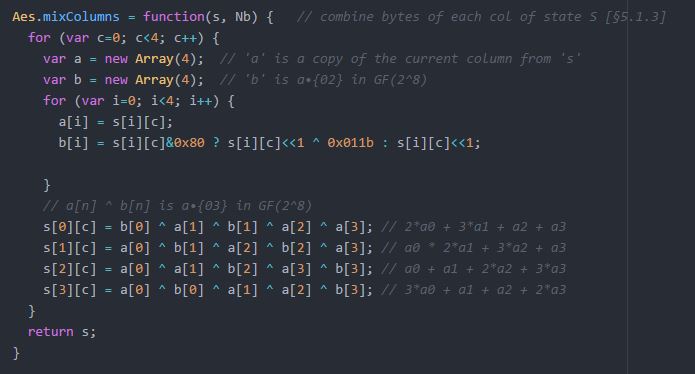
Figure 3.5 Illustrates the  Mix Column Function as elaborated in the AES Implementation.

3.7.7  Mix column keys combination

Figure 3.6 Encryption Key Bits of the AES algorithm which enhances the key strength combination.

 

Figure 3.7 Cache memory implementation

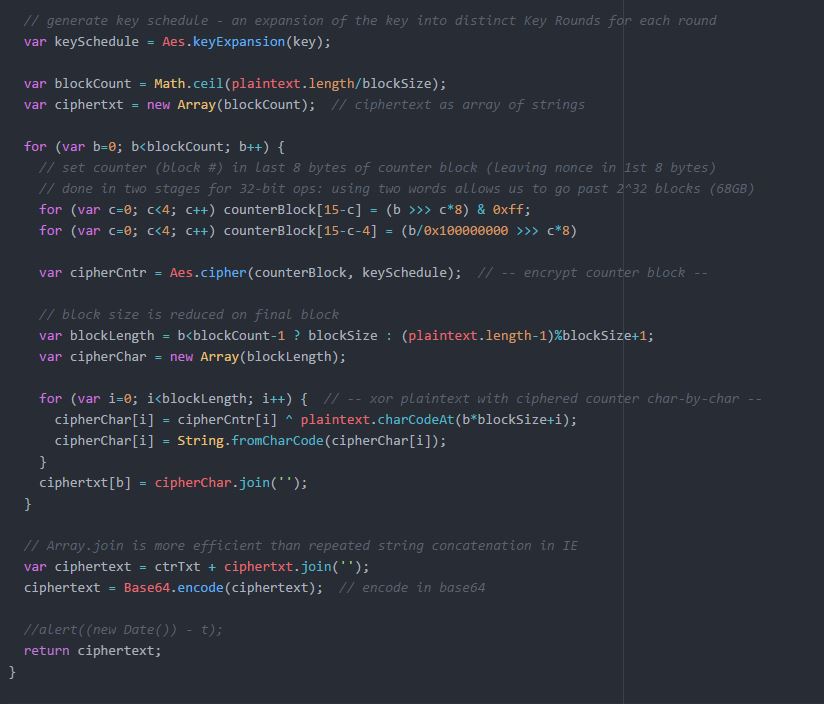
Figure 3.8 Rehashing implementation

CHAPTER 4

RESEARCH FINDINGS AND DISCUSSIONS

4.0  Introduction

After reviewing prerequisite knowledge in chapter two of this work, I present a critical analysis of the potential of mix column using 128, 192, 256-bit keys combined to be adopted as a symmetric key function regarding performance, memory usage and strength.

In this research work, I have implemented mix column algorithm, together with the mathematics behind that is time complexity and space complexity. This chapter describes the findings obtained in performance, memory usage and strength and also implementations on CPU throughput and execution time.

4.1 Key bit combination

The implementation of the 128,192,256 bit keys combination gives additional security features to the encryption and decryption of AES mix column.

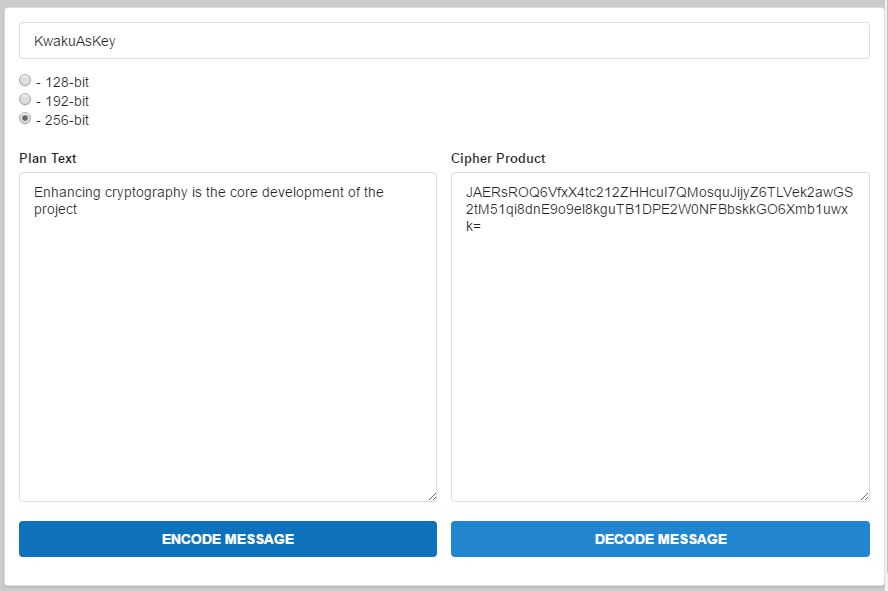
Figure 4.1 Graphical representation of the 128, 192,256 key bits which add on as key strength combination.

In figure 4.1 shows the graphical representation of the 128,192 and 256 key bits combined. From the illustration, user A communicating with user B can decide to choose  one of three keys which indeed changes the pattern of the encryption key. The key bits combination is one which help to reduce the attacks on data.

As per literature reviewed on AES functions, it was observed that most encryption algorithms implemented use only one of the following keys either 128 or 192 or 256-bit keys which was prone to attacks.

4.2  Rehashing

In addition to the cryptographic algorithm is rehashing function. In figure 4.2 and 4.3 gives details of the rehashing of the encrypted data which changes the state of the data in operation to serve as an add-on data security. For example in the plaintext column, when you type in any sentence or word together with an encryption key, when you encrypt the data it give you a cipher text. This cipher text can be rehashed so many times before it is sent across the network or internet. This feature in addition to the key bits combined make the cryptographic algorithm more secured.

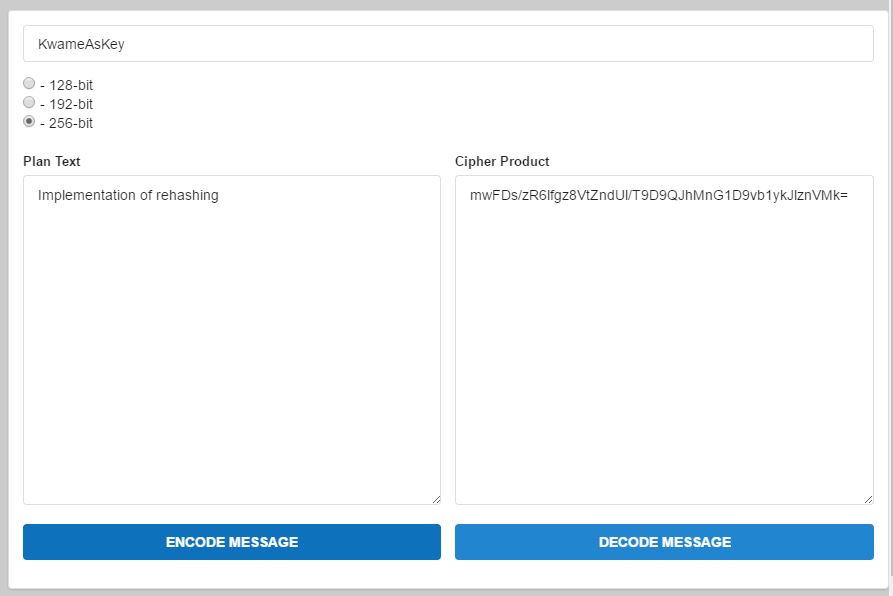
Figure 4.2 Graphical of the First Harsh of the rehashing of the cipher text.

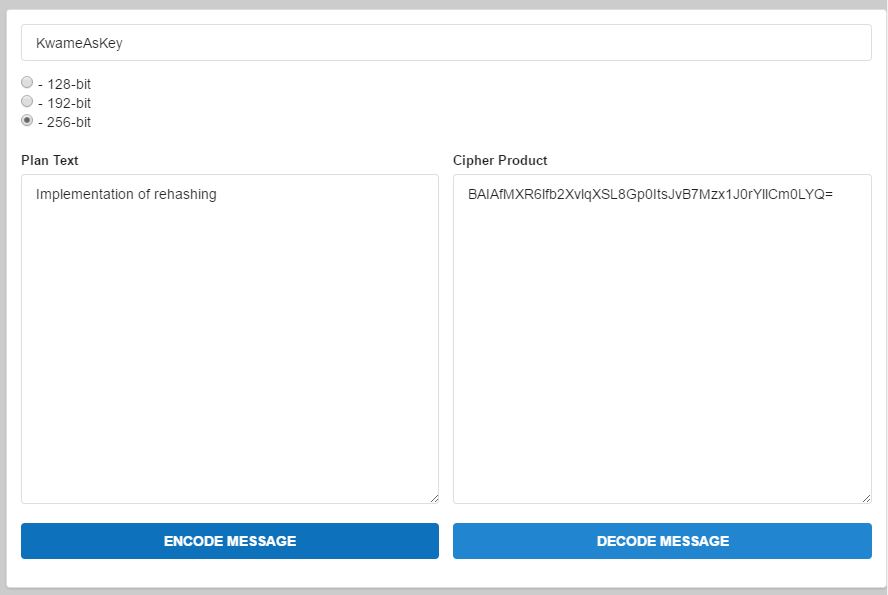
Figure 4.3 The implementation of the of the 256 bit key rehashing of the AES Encryption as elaborated in figure 4.1.

4.2  Cache Memory

The implemented encryption as illustrated in the figure 4.4 shows encryption reliance on cache memory other than accessing primary memory which acts as enhancing security buffer as illustrated in  venerability of data been checked by evaluating the correlation between the logical and physical addresses of the primary  memory encryption as illustrated in  figure 2.9. However   performance have been accelerated since the  encryption and  decryption was carried out with cache memory. The user has the ability the view whatever data that has been encrypted in the cache memory. The cache memory allocation has the ability to store ten (10)  different data encrypted and  this data are not stored in the main memory.

As per  the literature reviewed , most AES encryption uses main memory for encryption and decryption  other cache memory (Bruce Schneier,1996).

Figure 4.4 Graphical Representation of the Cache Memory

4.3 Result Summary

After successfully conducting an experiment on mix columns which implement the three parameters  (Key bits combined, rehashing and cache memory). The experiment conducted show that, the implementation of the key bits combined, rehashing and the use of cache memory in one cryptographic algorithm will enhance the strength and security data communication.

However, encryption with a one-bit key has its shortcomings such the attackers guesses the bit key and simulate the key but three keys 128, 192 and 256-bit being combined enhances the key strength of the cryptography.

Furthermore, as elaborated in this research, the main  memory has the tendency being compromised attacker such that physical address of the main memory could permit accessibility to attack, however in the research cache memory encryption was implemented to enhance the cryptographic algorithm as counter those adversaries.

CHAPTER 5

CONCLUSION AND FUTURE WORK

5.1  Summary

Cryptography has evolved over the last few decades, the need for effective encryption algorithm have become very demanding especially at data security level.

In this research, I have presented a novel enhanced implementation of the encryption algorithm AES utilizing of high performance Mix Column with key combination which uses properties of the binary calculation by provide maximum security with operation with the key strength combination of above mentioned algorithms are more secured and it also provides additional security of the system by improving the key length.

Have also implemented rehashing of key to improve the security of the system by rehashing of the cipher text.

The result shows the implementations allow me to increase flexibility, a satisfactory level of security for communication applications, or other electronic data transfer processes where security is needed.

5.2  Suggestions for Future Work

The research was carried out in a laboratory and though a small network was created in the laboratory to test the application, it was not a true representation of the real life situation where it will be situated on the internet and being able to be accessed from anywhere in the world. Factors that can affect the performance of and internetwork were not faced during this research since it was tested in a LAN.

Also the workload from request on the remote workstation was small compared to what will be the case upon deployment on the internet so the resources on the server computer were not a true representation of what load they will be required to handle.

5.3  Suggestions for Future Work

Attention must be paid to the exploration of better improvement in the software and hardware in foreseeable future. One realization that was made in the implementation of this work was that sometimes the implementation comparison is made on an optimal data structure on cryptography function optimized.

Also, the codes used in the research were only implemented in a single experimental environment. They could have been implemented tested on various platforms to evaluate their performance.

The ream of the future is not an easy one in making mix column cryptography algorithm with the three parameters (key bits combined, rehashing and cache memory) more efficient and secure way to communicate ; only time will tell what the fate of algorithm encryptions

Lastly, the use of enhanced AES mix column cryptographic algorithm with key bits, rehashing and cache memory seems to very have a promising future