Table of Contents

1 Introduction

1.1 Motivation

1.2 Objectives

1.3 Structure of Thesis

2 Literature Review

2.1 Overview of Titanium

2.1.1 Classification of Titanium

2.1.2 Formability of Titanium

2.2 Deformation Modes in Titanium

2.2.1 Slip Modes

2.2.2 Twinning

2.2.3 Texture Evolution

2.2.4 Strain Hardening Behavior

2.3 Grain Size Reduction

2.4 Dynamic Recrystallization

2.4.1 Factors Influencing Dynamic Recrystallization

2.5 High Strain Rate Rolling

2.5.1 Deformation Mechanism

2.5.2 Effects of HSRR on Magnesium

1         Introduction

Titanium is a remarkable metal with many favorable characteristics such as its outstanding specific strength, corrosion resistance and biocompatible nature. When considering such characteristics, titanium has significant potential to be used widely across various sectors. However, due to the poor formability of titanium and its alloys, it has limited industrial usage [1].

The poor formability of titanium can be attributed to its crystal structure. Titanium has a hexagonal closed packed system which does not have the minimum of 5 independent slip systems required for homogeneous strain deformation. Moreover, this issue of limited slip is intensified due to titanium’s tendency of developing strong deformation textures when deformed during processing, further hindering free plastic deformation[1].

To combat this limitation brought about by its HCP crystal structure, a high strain rate rolling (HSRR) processing method has been developed and experimented with in the University of Sydney. This method has been shown to enhance the formability and mechanical properties of other HCP metals such as Magnesium. With current research of this processing method being focused on titanium, if viable, this process may be implemented at an industrial scale, allowing for the more widespread use of hexagonal close packed metals.

1.1      Motivation

Traditionally, severe plastic deformation methods (SPD) such as equal channel angular pressing (ECAP) and surface mechanical attrition (SMAT) have been used to process fine grained titanium alloys[2]. However, these SPD methods are cost intensive and are difficult to implement at an industrial scale. Conventional processing methods such as cold rolling tend to leave behind a strong deformation texture which reduces slip and increases the anisotropy of titanium[3].

High strain rate rolling has shown promising preliminary results in enhancing the plasticity and refining the grain size of titanium. Moreover, the twinning induced dynamic recrystallization that occurs during the HSRR process has been studied to consumes the stored deformation energy, leaving weakened texture which is easier to deform.  Considering that the basic, manufacturing procedure of HSRR is similar to traditional cold and hot rolling methods, if progressed further, the HSRR method is one that could be industrially viable, enabling the widespread use of titanium.

Currently the effects of the high strain rate rolling method are being studied on titanium and its alloys. This thesis aims to contribute to that study by characterizing the effects of HSRR on the microstructure and mechanical properties of commercially pure titanium (cp-titanium).

1.2      Objectives

This study is performed with the aims of fulfilling the following objectives,

1. To characterize the effect of high strain rate rolling on the microstructure of cp-titanium.
2. To quantify the mechanical properties of high strain rate rolled cp-titanium and relate mechanical properties to processing parameters. Particularly to investigate the strain hardening behavior of HSRR processed cp-titanium

As observed from the set objectives, this study aims to study both the micro structure and mechanical properties of cp-titanium processed with HSRR. Of the mechanical properties, the strain hardening behavior is of particular interest as preliminary results of high strain rate rolled titanium displayed very little strain hardening. Therefore, to investigate this behavior, the strain hardening behavior of the titanium used in this project will be closely studied.

1.3      Structure of Thesis

This section will provide a brief description of each chapter included in this thesis

Chapter 2, Literature review

The literature review is split into four sub-chapters. The first of which will provide a brief overview of titanium and its different classifications. The second sub-chapter will detail the deformation modes and related mechanisms of titanium. Then in the third sub-chapter, separate mechanisms of interest such as strain hardening behavior and dynamic recrystallization will be discussed. The fourth and final sub-chapter of the literature review will provide an overview on the HSRR process.

Chapter 3, Experimental Design

This chapter is set in place to outline the experimentation and analysis methods used on the titanium samples. Firstly, in this chapter, the steps taken to prepare the titanium samples will be provided. Specifications such as electropolishing parameters and mechanical polishing parameters will be provided. Next, the steps taken to receive the electron image and the EBSD data for the titanium samples will be provided. Finally, the basic parameters and settings used in the visualization software will be specified.

Chapter 4, Results and Analysis

The results and analysis chapter will be split into 3 sub-chapters. The first of which will provide a overview of the various analysis methods used. In this section, the purpose behind the use of each of these analysis methods will also be made clear. Next, the results and data regarding the micro structure of the titanium samples will be provided. This sub-chapter will contain data on grain size, texture, twinning and other parameters relating to the titanium microstructure. The third and final sub-chapter will provide the results and data regarding the mechanical properties of the titanium samples. This will include details regarding the strength, ductility, strain hardening behavior and the overall stress-strain related details.

Chapter 5, Discussion

The discussions chapter will attempt to piece together all the results attained. Relating to the aims of this project, this chapter attempts to relate the microstructure of the titanium samples to their specific thermomechanical processing conditions. Moreover, this chapter will contain a sub-chapter devoted to discussing the staring hardening behavior of the titanium samples.

Chapter 6, Conclusion

The conclusions chapter of the thesis will summarize the key points and findings of this project. It will also contain recommendations for any future research that may be conducted for the high strain rate rolling of titanium.

2         Literature Review

2.1      Overview of Titanium

Titanium is an allotropic element which can exist in more than one crystallographic form. At room temperature, titanium possesses a hexagonal close packed (HCP) micro-structure, referred to as its alpha(α) phase. At 882.5ᵒC, its beta(β)-transus temperature, titanium undergoes an allotropic transformation from the HCP structure to a body-centered cubic (BCC) [4]. When in exhibiting the BCC crystal structure, titanium is referred to as being in its β phase. The addition of alloying elements into to pure titanium can alter the transformation temperature of titanium.

2.1.1     Classification of Titanium

Alloying elements are generally classified as α stabilizers or β stabilizers depending on how they influence the beta-transus temperature of titanium. As shown in Figure.2-1a, alpha stabilizing elements such as aluminum and carbon tend to increase the beta-transus temperature of titanium. These elements favor the alpha phase and stabilize it by increasing the beta-transus temperature. On the other hand, beta stabilizing elements such as iron, chromium and cobalt tend lower the beta-transus temperature. In all, titanium and its alloys can be broadly classified into four categories . Namely, they can be classified into alpha, near-alpha, alpha+beta and beta alloys [5, 6].

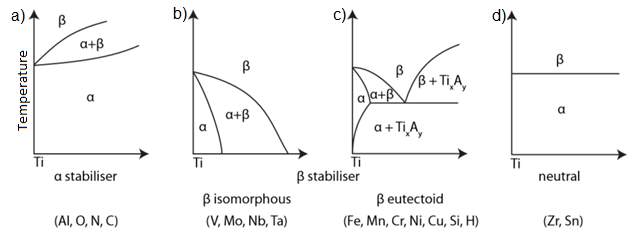
Figure 2‑1: Effects of alloying elements on titanium. (a) Alpha Stabilizers (b) Beta isomorphus stabilizers (c) Beta eutectoid stabilizers (d) Neutral stabilizers [7]

2.1.1.1     Alpha Alloys

Alpha titanium alloys consist of both pure titanium and alloys containing α-stabilizing elements. The primary alloying elements associated with alpha titanium are aluminum, oxygen, nitrogen and carbon. As seen in Figure.1a, the increased addition of these alpha stabilizing elements will increase the beta-transus temperature of titanium. Alpha titanium alloys typically display limited formability due to their hexagonal closed packed structure [4]. However, this is a parameter that is known to vary considerably in relation to the alloying elements involved [8].

The most commonly used alloy of this category is commercially pure titanium(cp-titanium). Being the subject of this project, commercially pure (cp) titanium is of particular interest. Though being identified as pure, cp-titanium is in fact a Ti-O alloy with oxygen acting as an α-stabilizer. CP-titanium typically has oxygen content varying between 0.18% to 0.40%, with higher oxygen content resulting in increased tensile strength while compromising formability[4, 8, 9].Since cp-titanium and other alpha alloys are single phased, they exhibit relatively low tensile strength, especially for low oxygen contents. It should also be noted that cp-titanium exhibit high rates of strain hardening [4].

2.1.1.2     Near Alpha Alloys

Near alpha alloys were developed to enable titanium to operate at higher temperatures. This category of alloys typically exhibit higher tensile strength that alpha alloys. They also display the best creep resistance of all titanium alloys at temperature above 400°C. Since this category of titanium alloys are usually forged and heat treated in the alpha + beta phase, there are always some beta grains remaining in their microstructure [4].

2.1.1.3     Beta + Alpha Alloys

Beta + Alpha alloys consist a moderate amount of beta stabilizers to lower the beta-transus temperature and ensure that the beta phase is retained at room temperature. They typically exhibit the ductility associated with beta alloys while retaining the strength of alpha alloys [4, 10]. Moreover, their microstructure and properties can be molded extensively by the implementation of heat-treatment or thermomechanical processing. The most famous (α + β) alloy is Ti-6Al-4V, accounting for 60% of all titanium production [11].

2.1.1.4     Beta Alloys

Beta alloys are defined as alloys containing enough beta stabilizers to allow the beta phase to be retained in either a stable or metastable condition at room temperature after cooling [4]. As seen in Figure.1b & c, beta stabilizing elements can be categorized into β eutectoid and β isomorphous elements. Isomorphous stabilizers such as vanadium, tantalum, and niobium are miscible in the beta phase and sufficient concentrations of these elements enables the β phase to be present at room temperature [4]. Eutectoid stabilizers form eutectoid systems with titanium and significantly reduce the beta-transus temperature of titanium. In comparison to alpha alloys, due to the BCC structure of the beta grains, beta alloys exhibit superior forming characteristics. This allows for them to be easily cold rolled and strengthened by age hardening.

2.1.2     Formability of Titanium

The plastic deformation behavior of titanium is very closely related to its crystal structure. Below the β-transus temperature, the HCP structure of α-titanium causes anisotropic mechanical behavior [12]. In particular, elastic anisotropy is distinctly pronounced. Depending its crystallographic orientation, the Young’s modulus of titanium varies considerably. Across literature, the Young’s modulus of single crystal titanium varies consistently between 145GPa vertical to the basal plane and only 100Gpa in parallel to the same plane [12, 13].

In general, plastic deformability decreases from BCC to the HCP lattice. This phenomenon can be attributed to the reduced number of independent slip systems that the HCP structure possesses compared to the BCC structure. The HCP structure only has 4 independent slip systems whereas the BCC structure has a total of 12 independent slip systems [12]. Since von Mises criterion stipulates that a minimum of 5 independent slip systems are required for homogeneous strain deformation without volume change within a polycrystal, HCP structured α-titanium often displays poor plastic deformability [14]. This lack of independent slip systems explains the poor plastic deformability of HCP α-titanium as compared to BCC β-titanium.

With the capability to transform from the α phase to β beta, titanium offers the prospect of having alloys with the α, β or mixed α/ β microstructures. However, beyond this point, this literature review will be restricted to α-titanium since only cp-titanium is used in this project. Also, this literature review will mainly focus on the HCP crystal structure, since the cp-titanium being used is processed comfortably below its beta-transus temperature at all stages of experimentation for any beta phase to be present.

2.2      Deformation Modes in Titanium

Talk about 2 major modes of deformation. Slip and twinning.

2.2.1     Slip Modes

Slip is the DEFINE

The primary slip planes and slip direction in α-titanium are provided in Figure.2-2a below. Titanium primarily slips in the three close packed directions of the

<112¯0>type along its <a> basal, <a> prismatic and <a> pyramidal planes. The active slip planes in HCP titanium are its

(0002)basal plane, its six

101¯1pyramidal planes and its three

101¯0prismatic planes [11]. Accounting for the possible slip directions alongside the slip planes, there are a total of 12 possible slip systems. However, due to the combined actions of some slip systems replicating the movement of other systems, there are only four independent slip systems in HCP titanium [10, 11].

Figure 2‑2 : a) Primary slip planes and directions in HCP titanium, b) Secondary slip planes and directions [11]

Since von Mises criterion stipulates that a minimum of 5 independent slip systems are required to accommodate arbitrary plastic deformation, the activation of further deformation modes are necessary for titanium to accommodate its imposed strain [10].Typically, twinning or secondary slip systems such as <c+a> pyramidal slip can be used to accommodate plastic deformation in titanium [10, 15, 16]. The secondary <c+a> pyramidal slip systems are provided in Figure.2-2b.

The activation of slip in a stressed material is dependent on the Schmid Factor.  The Schmid factor is used to account for the grain orientation in relation to the loading axis so as to effectively calculate its critical resolved shear stress (CRSS). The Schmid factor can be calculated using the equation below,

m=cos∅.cosλ

where m is the Schmid factor,

∅is the angle between the loading direction and the normal to the slip plane and

λis the angle between the slip direction and the loading direction [11]. Figure.2-3 below shows the relationship between loading direction, the slip direction and the normal direction with respect to the slip plane. Once the Schmid factor (m) is resolved for, it can then be used to calculate the resolved shear stress.

τc=σy.cos∅.cosλ

Where

τcis the CRSS and

σyis the yield stress. As the applied load is increased, the resolved shear stress increases in each slip system till CRSS is eventually reached. When the CRSS of a particular slip system is reached, the system will become active and the material will begin to deform through slip [11].

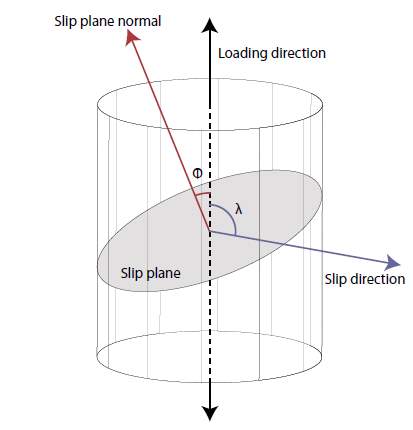
Figure 2‑3 : Schematic representing the loading direction, slip direction and slip plane normal [11].

In α-titanium, the lattice parameters of the HCP structure are a=0.295nm and c=0.468nm. Due to these parameters, the c/a ratio of HCP titanium deviates considerably the ideal HCP lattice c/a ratio of 1.633[12, 13]. In comparison to ideally packed HCP crystals, the reduced c/a ratio of α-titanium implies larger spacing distances between the prismatic planes [12]. This in turn indicates that the relative packing density of the basal plane is lower than the prismatic plane, thus favoring slip in the more compact prismatic plane rather than the basal plane. This is notion further validated when observing the critical resolved shear stress(CRSS) of titanium. As shown in Figure.2-4 , where the experimental data from various studies are compared, at a temperature of 300K, the CRSS of for prismatic slip activation in titanium is only a quarter of the CRSS required for basal slip activation, thus favoring slip in the prismatic plane [17, 18].

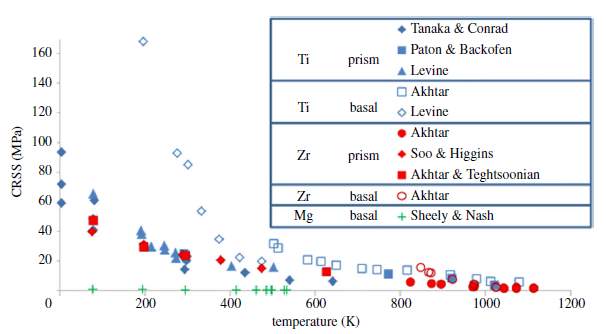
Figure 2‑4 : CRSS values for basal and prism slip in Ti [17, 18].

From observing Figure.4, the relationship between temperature and slip deformation can also be understood. It is evident that with increasing temperature, the CRSS for the prismatic and basal slip activation decrease and converge to almost identical values. This suggests that both prismatic and basal slip will be active when titanium is deformed at elevated temperatures.

The c/a ratio of α-titanium can be increased slightly by the insertion of interstitially dissolved atoms such as carbon, nitrogen or oxygen atoms. Similar results can be also be observed by incorporating of substitutional atoms with smaller atomic radius, such as aluminum [12, 13, 17].

2.2.2     Twinning

In general, slip in HCP structures are limited due to their low symmetry and lack of independent slip system. Due to this, it is often necessary for twinning to occur alongside slip to accommodate for complete deformation of the HCP structured material [19, 20]. Moreover, the plane reorientation that occurs due to deformation twinning allows for further slip to occur in the crystal structure.

In short, deformation twinning can be defined at the collective shearing and reorientation of one portion of a crystal structure. The shearing and reorientation of the parent crystal occurs across particular lattice planes and in specific directions. The twinned structure is highly symmetrical across the twinning plane, often both sides being mirror images of one another. Contrary to deformation thorough slip, where crystallographic orientation remains unchanged, deformation through twinning involves the reorientation of a small distinct segment of the crystal lattice [21].

There are various twinning modes that can accommodate deformation in HCP materials. These modes can be broadly split into two groups, namely, compression twins and tension twins. The naming of these twinning groups describes the strain generated by the twin system on the parent crystal along the <c> axis. HCP titanium is commonly observed to undergo deformation twinning on the

101¯1, 101¯2,112¯1and

{112¯2}planes [22, 23]. The

112¯1and

101¯2twins result in extension of the <c> axis, whereas, the

{101¯1}and

{112¯2}twins result in the contraction of the <c> axis. These twin modes and their associated misalignment angles are depicted in figure.2-5 below[11].

Figure 2‑5: Common twinning modes in HCP titanium [11].

According to Olaf & Valeria, the most commonly occurring twinning system in HCP titanium is

101¯2<1̅011>[24].  Due to this particular twinning system requiring the smallest magnitude of activation shear stress, it is the most easily activated of the four commonly observed types. Apart from the four common twins depicted in figure.2-5, deformation twinning has also been less commonly reported in the

112¯3and

112¯4modes [25]. Of particular interest to this project, as per research conducted by the University of Cambridge in 2015, high area fractions of

112¯4twinning have been observed under high strain rate deformation of titanium [26]. However, the scientific evidence for the

112¯3and

112¯4twinning modes are much less robust and frequent than the four commonly occurring twin modes. Therefore, their occurrence in experimental results of this project will be critically analyzed and discussed.

Aside from accommodating the overall plastic deformation, twinning also plays two further roles in α-titanium. Firstly, due to the reorientation of twinned areas, twinning is the primary contributor to the texture evolution of the deformed titanium [27]. Secondly, twinning is a major influencing factor to the strain hardening behavior of the α-titanium [28]. These two mechanisms will be discussed further into this literature review.

The function of deformation twinning in the fracture behavior and ductility of HCP metals has been the focus of numerous investigations [16, 18, 26-28]. Due to the complex interrelationships between twinning, slip and fracture behaviors of HCP structure, the effect of twinning on fracture behaviors are ductility have been hard to isolate. Moreover, with many various parameters such as temperature, strain rate, grain size, stacking fault energy(SFE) and CRSS affecting twinning behavior [25], there is no definite template to correlate twinning and material behavior in HCP titanium. Therefore, the twinning modes observed in the experimental results of this project will be analyzed and correlated to their thermomechanical processing conditions as best as possible.

2.2.3     Texture Evolution

1 Define Texture, and coordinates, 2 Texture evolution in titanium, 3 Texture evolution in hot rolling

Polycrystalline materials often display preferred crystal orientations, this preferred orientation is referred to as the texture of the material [29].  The texture of a material has a strong influence on the various mechanical and structural properties that it displays. According to H.J.Bunge (1987), texture can affect the mechanical properties of a material by as much as 20-50% of the property’s value [30]. Characteristics such as tensile strength, ductility, toughness, Young’s modulus and Possion’s ratio are examples of properties that are influenced by the average texture of a material [24].

The texture in a material may be developed through various processes such as plastic deformation, annealing and phase transformation. Therefore, through the implementation of such processes, it is possible to alter the texture of a material to enhance particular properties. For the case of a thermomechanical process such as HSRR, plastic deformation will be accommodated through slip and twinning at elevated temperatures.  As the plastic deformation progresses, slip will cause the lattice to rotate into a preferred orientation, resulting in texture [31].

The texture evolution in HCP metals is highly dependent on their c/a ratio and associated dominant slip systems [32][32]. For magnesium and other HCP metals with c/a ratios near the ideal value of 1.633, the cold rolling texture is dominated by strong {0001} basal fiber textures, as seen in Figure.##a.  Due to these metals predominantly slipping in the basal direction, their grains rapidly rotate to {0001} and reduce other twinning and slip possibilities [33, 34]. On the other hand, HCP metals with a c/a value higher than 1.633, such as zinc, have their basal plane tilted to the rolling direction by about 20 to 30 degrees, as shown in Figure ##b. In the case of titanium, which has a lower than ideal c/a ratio of 1.588, the basal plane is tilted by 30 to 40 degrees with a rotation axis of

<101¯0>parallel to its rolling direction [35].

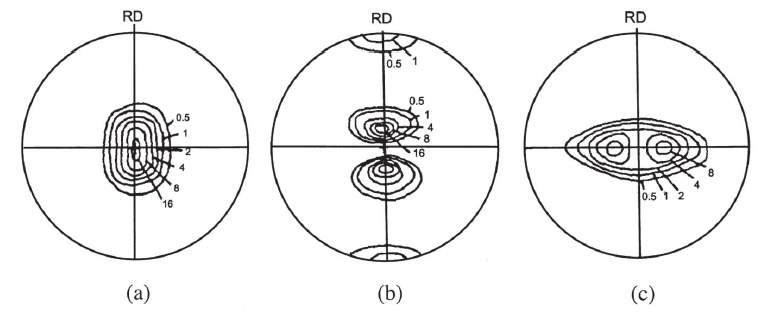
Figure 2‑6 : Texture of (0002) pole figures in cold rolled HCP metals, (a) Magnesium c/a ideal, (b) Zinc c/a high, (c) Titanium c/a low [36]

Cold Rolling Texture

The texture evolution of commercially pure titanium at different rolling reduction levels can be seen in Figure.4. This figure shows the experimental results of Bozzolo et al, where the texture evolution of commercially pure titanium was measured from the fully recrystallized state to 80% reduction under cold rolling [##].

Knight, 1978; investigated the

texture evolution of commercially pure titanium sheets after cold rolling at 21.4% and 89.4% of

reduction and observed that the most intense texture component, for both degrees of reduction

was the (2115) [0110].

 

2.2.4     Strain Hardening Behavior

In relation to the objectives of this project, the strain hardening behavior of titanium is of particular interest. Therefore, this section will detail strain hardening behavior and the factors that affect it.

Strain hardening or work hardening refers to the increase in instantaneous stress required to continue deformation at any instance during plastic strain [37]. The phenomenon of strain hardening tends to increase the load carrying capacity of a material as deformation increases, till the point of ultimate tensile strength. This behavior can be seen in figure 2-7, where the increase in load carrying capacity due to strain hardening is indicated. It is vital to understand the mechanics and inner workings of strain hardening due to its influence on the fracture properties and deformability in materials.

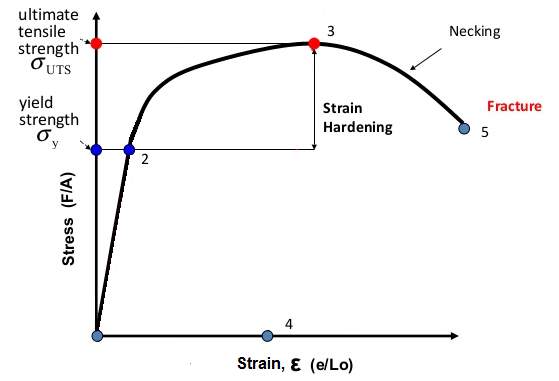
Figure 2‑7 Strain hardening in the stress-strain curve

Strain hardening arises from the interaction of dislocations with one another. During deformation, when dislocations that run along dissimilar planes encounter each other, they are unable to pass through and are rendered immobile within the crystal lattice. Subsequently, unable to pass, the dislocations pile up and become intertwined. With the pile up and entanglement of dislocations, the particular grain is unable to deform further without the input of significantly larger stresses [36].

The relationship between strain hardening, strain and the strength of the material during plastic deformation can be approximated using the power law equation provided below,

σ=Kεn

Where K is the strength coefficient, is the

The strain hardening

coefficient increases with the increase in strain. The yield strength and the strain hardening increases with the

increasing strain rate at a fixed temperature but decreases with increasing temperature for a given strain rate. Role

of strain rate and temperature is highly significant in determining strain hardening behaviour and formability of

material. Lee et al. have shown that at constant temperature, the flow stress, strain hardening rate and strain rate

sensitivity increases with increase in strain rate.

The strain hardening behavior of polycrystalline α-titanium under compression and plane strain compression has been studied extensively by Salem et al[28, 38-40]. As shown in in figure.2-8, Salem segments the strain hardening behavior of titanium into three distinct phases. In the first phase, Stage A, the deformation of titanium is accommodated predominantly by slip. In this phase, the activation of basal slip and prismatic slip with common slip direction remove the defects in the crystal lattice, resulting in dynamic recovery and in turn lower rates of strain hardening. In this phase, in this phase, the < c+a > pyramidal slip is activated to constitute the five independent slip systems require for uniform plastic deformation.

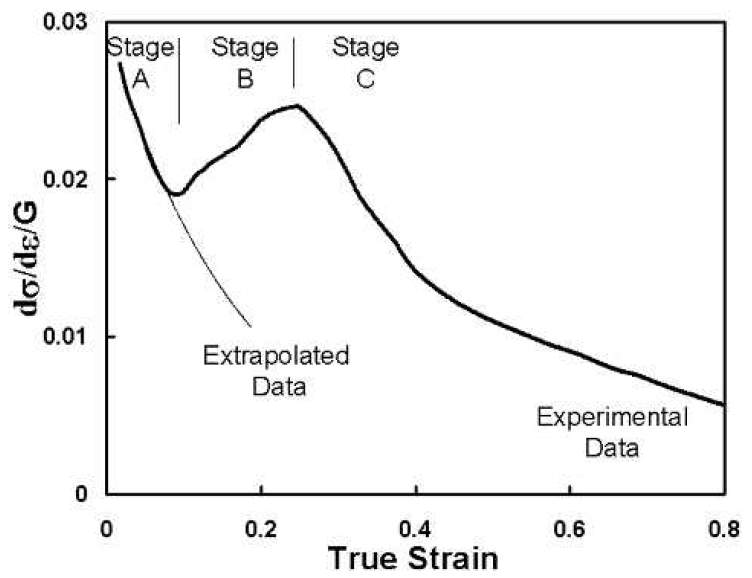
Figure 2‑8: Strain hardening rate against strain for cp-titanium [38]

In Stage B, both twinning and slip occur concurrently to accommodate the deformation of titanium. During this phase, the average effective slip distance is expected to be reduced due to the grains being divided by the existence of twin boundaries. Due to the reduction in effective slip distance, the flow stress, the stress require for continuous plastic deformation, is raised. As a result, the strain hardening rate of titanium is typically expected to increase in this stage. In the final phase of strain hardening, Stage C, cp-titanium exhibits decreasing strain hardening rates. Though the exact mechanism is not known, it is theorized that the decrease in strain hardening rate is driven by saturating twin volumes. Due to extensive twinning in the previous stage, twin volumes saturate and new twins are not produced as readily. With increasing difficulty in producing twins, the imposed strain is largely accommodated by slip. As in Stage A, this results in dynamic recovery and in turn lowers the strain hardening rate.

This three-stage strain hardening behavior of titanium proposed by Salem has been reported to occur in numerous other studies, such as studies conducted by Nasser et al. and Kailas et al. [41-43]. Despite these supporting studies, there is no concrete evidence that this three-stage strain hardening phenomenon might not be present in the cp-titanium that is processed with HSRR. All the aforementioned studies that supported Salem’s three-stage strain hardening behavior typically had grain sizes averaging at approximately 30 microns. On the other hand, due to the grain refinement that occurs due to dynamic recrystallization, the post HSRR processed titanium is expected to have a considerably smaller grain size. Since grain size is an important factor affecting strain rate, for this project, the proposed three-stage behavior is not fully convincing. Moreover, as will be explained in the next section, grain size has a strong influence on the strain hardening behavior.

2.3      Grain Size Reduction

One of the reason why HSRR is so appealing is because the it is able to reduce the grain size of the material being processed. The reduction in grain size is known to several effects on the properties of titanium. This section will describe the relationship between grain size and other material properties.

Across numerous studies, it has been shown that titanium follows the Hall-Petch relationship[44, 45]. The Hall-Petch equation relates the grain size of a material to its yield strength,

σy=σ0+kyd

Where

σyis the yield stress,

dis the average grain diameter, k_y is the strengthening coefficient and

σ0is a material constant. As observed in the Hall-Petch, yield stress and grain diameter have an inverse relationship. Suggesting that a decrease in average grain diameter will increase the yield stress of a material.

Apart from the Hall-Petch equation, experimental studies comparing cp-titanium with various grain sizes have shown that as grain size decreases, the yield strength of titanium increases. The relationship between grain size and yield strength can be gathered when viewing figure 2-9. Figure 2-9 shows the experimental results of Salishchev and Mironov {Salishchev, 2001 #65}. As seen on the diagram, with a titanium of smaller average grain size displays higher yield strengths.

Other than the yield stress, grain size also has a significant influence on strain hardening. Referring to Figure 2-9 again, the general relationship between grain size and strain hardening can be gathered. As the average grain size in a material decreases, both the flow and yield stress increase without any increase in strain hardening {Gupta, 2015 #37}. Due to this, when the grain size is reduced beyond a point, there is no apparent strain hardening behaviour. As seen in the case of the 0.4µm and 0.5µm grains in figure 2-9.

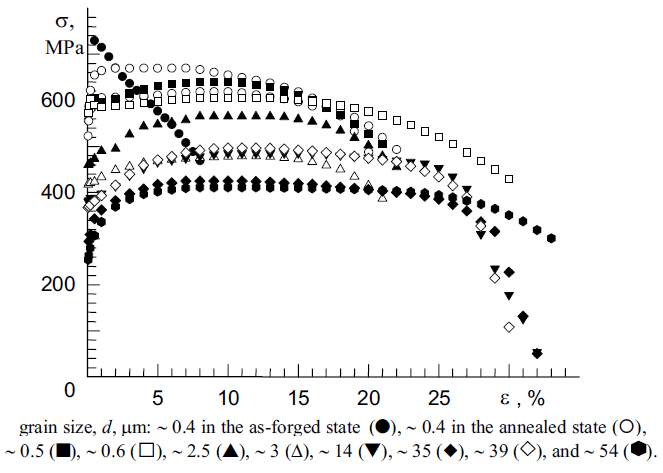
Figure 2‑9 Tensile stress-strain diagram for cp-titanium specimens with various grain sizes {Salishchev, 2001 #65}

 

 

 

 

 

2.4      Dynamic Recrystallization

Recrystallization, as defined by Doherty et al., is defined as the formation of a new grain structure within a deformed material through the formation and migration of high angle grain boundaries driven by the stored energy of deformation [46]. When the process of recrystallization occurs during deformations at elevated temperatures, is termed Dynamic Recrystallization (DRX)[47]. DRX is a driving phenomenon behind the microstructural changes that occur to titanium during the HSSR process. This section will discuss the DRX process and the factors that influence it.

The DRX process can be categorized into three distinct types, namely, discontinuous dynamic recrystallization (DDRX), continuous dynamic recrystallization (CDRX) and geometric dynamic recrystallization (GDRX). DDRX is frequently observed for materials with low stacking fault energy, strain free grains grow and spread in regions of full dislocations[48]. On the other hand, CDRX and GDRX are processes which are observed much more frequently in materials with high stacking fault energy. In CDRX, dislocations are progressively accumulated into low angle grain boundaries(LAGB). This accumulation of dislocations increases the misorientation of the LAGBs till a critical value and transforms them into high angle gran boundaries (HAGB).   In the case of GDRX, it can be described as the formation of a new more refined grain structure through the migration of HAGBs to form serrations.

Of the three DRX categories described, CDRX and GDRX are of more interest than DDRX. Due to titanium having a very high stacking fault energy of 300mJ/m² [49], it is more likely that the HSRR processing technique will result in one of either CRDX or GDRX.

2.4.1     Factors Influencing Dynamic Recrystallization

There four primary factors that influence dynamic recrystallization. Namely, these factors are stacking fault energy (SFE), initial grain size, thermos-mechanical processing conditions and second phase particles. The effects of these factors will be discussed in this section.

2.4.1.1     Stacking Fault Energy

A stacking fault is any defect or abnormality which alters the sequential nature of a layered crystal structure [2]. The stacking fault energy is the amount of energy that is carried by these defects within a material. The stacking fault energy (SFE) of a material is a factor that has significant impact on the DRX process. In particular, the SFE of a material determines the extent to which unit dislocations can dissociate to partial dislocations.

It should be noted that the accurate quantification of the SFE of a material is a very difficult due to the small separation distances of partial dislocations[50, 51]. However, the basic correlations between stacking fault energy and dynamic recrystallization behavior has been observed. According to Humphreys et al. and Huang et al., in materials with high stacking fault energy, such as titanium, the separation of perfect dislocations into partial dislocations is very difficult [47, 48]. Therefore, during DRX, dislocation glide and cross slip take place readily. Moreover, materials with high SFE, due to the occurrence of aggressive dynamic recovery during thermomechanical processing, dislocations are not able to accumulate sufficiently to sustain DDRX. However, materials with high SFE have been reported to display well developed subgrain structures with very limited dislocations[48]. Moreover, it has also been noticed that at larger strains, the misorientation of the subgrain boundaries increase progressively till they develop into HAGBs. This suggests that, under large strains, materials with high SFE will undergo CDRX.

2.4.1.2     Initial Grain Size

Apart from the stacking fault energy, the initial grain size of a material also primary factor that influences the occurrence of DRX.  Considering that grain boundaries hinder dislocation motion, it is possible to alter the difficulty of dislocation motion by varying grain size. Since much of the DRX process occurs or originates from the grain boundary , by varying the initial grain size,  it is possible to influence dynamic recrystallization behavior. In the case of DDRX, grain boundaries are the favored location for nucleation. Therefore, by increasing grain size and in turn reducing grain boundary area, the kinetics of DDRX may be lowered [48].

The effects of initial grain size on CDRX has not been studied as extensively as it has been studied in CDRX. However, several studies have shown that smaller initial grain size presents favorable conditions for CDRX [52, 53]. In these studies, it has been observed that smaller initial grain size tends to accelerate grain refinement and increase disorientation of LAGBs, creating favorable conditions for CDRX. It should be noted that recrystallized grain size does not depend on the initial grain size. Instead, it depends largely on the temperature and applied strain rate of the process [48].

2.4.1.3     Thermomechanical Processing Conditions

Thermomechanical processing (TMP) conditions are also a key factor that influence dynamic recrystallization behavior. For the purpose of studying dynamic recrystallization, both temperature(T) and strain rate (

ε̇) can be incorporated into the Zener-Hollomon parameter (Z) using the equation shown below,

Z= ε̇exp⁡QRT

Where R is the gas constant and Q is the activation energy for deformation. The Z parameter can then be related to the flow stress using the Sellars and Tegart constitutive equation,

Z=Asinhασn

Where

A,nand

αare material constants. Through both these equations, the thermomechanical processing conditions can be related to the flow stress.

Using these equations, the effect of TMP on the DDRX process has been understood to a considerable extent. It has been shown that at high temperatures and low strain rates, flow stress curves display multiple peaks in the DDRX regime. Conversely, at low temperatures and high strain rates, at the DDRX regime, flow stress curves only exhibit a single peak [48].

However, unlike DDRX, the stress-strain for CDRX and GDRX have been much less documented.  CDRX and GDRX require large deformations, often the deformation is imparted by severe processing methods such as high pressure torsion or equal channel angular pressing which do not allow for the recording of the stress-strain curve [48].

2.4.1.4     Second Phase Particles

Since second phase particles tend to greatly affect dislocation motion, they have a massive influence on DRX behavior. Fine particles tend to hinder boundary movement, reduce recrystallization rate and reduce the rate of grain growth. On the other hand, due to the large amounts of stored energy at deformation regions, coarse particles have been shown to increase the rate of recrystallization through particle simulated nucleation [48].

 

 

 

 

 

 

2.5      High Strain Rate Rolling

High Strain Rate Rolling (HSRR) is a relatively new processing technique that has shown to substantially improve the mechanical properties of magnesium and its alloys. The fundamental difference between traditional rolling methods and HSRR is that traditional rolling methods place their emphasis on strain, whereas, the HSRR process places its emphasis on strain rate. Since strain rate is a parameter that has significant influence in twinning behavior and dynamic recrystallization, it also has significant impact on the overall deformation of a material. This is especially true in the case of HCP materials such as titanium and magnesium, which often accommodate plastic strain through the activation of twins due to the limited number of slip systems they possess.

2.5.1     Deformation Mechanism

The working principle of HSRR can be understood by studying the deformation mechanisms that are in play during the thermomechanical processing method. Figure 2-8, below, provides a schematic that shows the evolution of deformation mechanisms during the HSRR process.

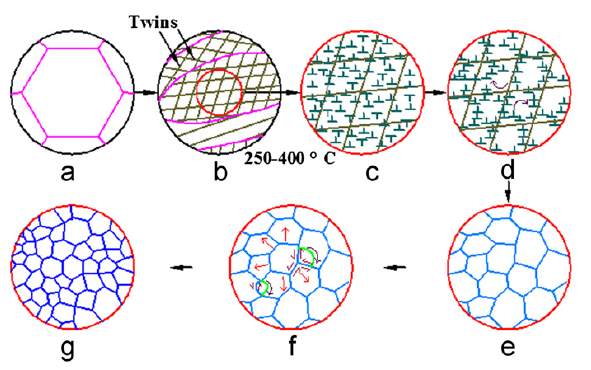
Figure 2‑10 :Schematic representing the evolution of deformation mechanisms during HSRR: a) initial coarse grain, b) formation of twins in original grain, c) high density dislocation in form in twin structure, d) reorientation of dislocations & reorientation of subgrains, e) continuous dynamic recrystallization, f) nucleation of discontinuous dynamic recrystallization, g) final microstructure [54]

Initially as shown in Figure2-8a & b, at the early stages of the HSRR process, due to the deformation at high strain rates, high density deformation twins appear in the original grain. As the deformation continues, the original grain is divided by the twins. At this point, twin lamellae and grids form containing high density dislocations, as shown in Figure 2-8c. With ideal processing temperatures, through dynamic recovery, these high-density dislocations rearrange themselves and accumulate, forming nucleation zones for continuous dynamic recrystallization (CDRX). With continued reorientation and accumulation, high angle dynamic recrystallization (DRX) grains are formed, as shown in Figure 2-8e. Due to the extensive twinning of the initial microstructure, CDRX occurs through the microstructure. With the onset of further deformation, as illustrated in Figure 2-8f, discontinuous dynamic recrystallization(DDRX) occurs at the grain boundary and prevents further grain growth. Finally, as seen on Figure 2-8g, a fine grained microstructure is attained.

By actively employing both twinning and dynamic recrystallization, the HSRR process is able to consume the large strain energy associated with plastic deformation and prevent cracking during the manufacturing process [54].

2.5.2     Effects of HSRR on Magnesium

Since the effects of HSRR has not been documented extensively on titanium, at minimum, the effects of HSRR on a similar material should be addressed. Therefore, this section will assess the effects of HSRR on HCP magnesium. Suqin et al., has conducted numerous investigation on the effect of HSRR on magnesium [54-57]. By analyzing her studies, the possible effects of HSRR on titanium can be gathered.  The general mechanical properties of ZK60 alloys processed under HSRR and conventional processing methods are provided below[56]. From observing this table, it is immediately observable that on the whole, ZK60 alloys which are processed with HSRR tend to display superior ductility to the alloys processed with conventional methods. Moreover, this increase in ductility is available while largely retaining its yield strength and tensile strength, suggesting the excellent strength to ductility balance that is attained by the use of HSRR. Suqin et al, attributes this excellent balance of strength and ductility to three factors. Namely, these factors are, grain size refinement, low dislocation density and weakened texture. By reducing grain size, the overall toughness of the magnesium alloy is improved. While ductility is improved by the weakened basal texture which can facilitate basal slip, and by low dislocation density which improves strain hardening rate.

Table 1:Mechanical properties of ZK60 alloy for various processing methods (Reference for HSRR[56])(Reference for conventional methods

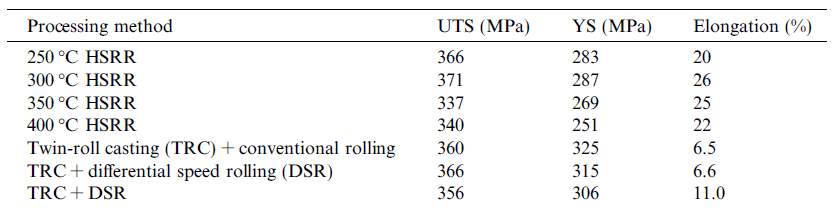
Apart from the study discussed, numerous other studies on magnesium have also shown the positive effects of HSRR on hcp materials. Often the processing of magnesium with HSSR yields fine grained microstructure with good homogeneity, low dislocation density and a weekend basal structure [54, 56, 57]. However, from analyzing these studies, it is also apparent that much research and analysis had to be conducted before the ideal thermomechanical processing parameters were derived.  One instance when is the case is when ZK60 was rolled under various strain rates to check for feasibility. It was found that ZK60 could be rolled successfully at low(≤2.9s^-1) or very high ( ≥ 7.8s^-1) strain rates. However, at medium strain rates (3.9-7.2s^-1), the ZK60 cracked profusely [55]. This suggests that significant research and experimentation considering various temperatures and strain rates have to analyzed before it can be successfully implemented on a new material. Therefore, as important as it is to observe and characterize the microstructure of high strain rate rolled titanium, it is also important correlate the relationship between the resultant micro structure and its processing parameters.

Stacking Fault Energy of titanium = 310 mJm^-2

1. Crosby, K., R. Mirshams, and S. Pang, Development of texture and texture gradient in Al-Cu-Li (2195) thick plate. Journal of materials science, 2000. 35(13): p. 3189-3195.

2. He, X.M., S.S. Zhu, and C.H. Zhang. Analysis of the Grain Refinement Mechanism for Commercial Pure Titanium by ECAP and SMAT. in Advanced Materials Research. 2014. Trans Tech Publ.

3. Fjeldly, A. and H. Roven, Observations and calculations on mechanical anisotropy and plastic flow of an AlZnMg extrusion. Acta materialia, 1996. 44(9): p. 3497-3504.

4. Polmear, I., Light alloys: from traditional alloys to nanocrystals. 2005: Butterworth-Heinemann.

5. Boyer, R., An overview on the use of titanium in the aerospace industry. Materials Science and Engineering: A, 1996. 213(1-2): p. 103-114.

6. Boyer, R., Titanium for aerospace: rationale and applications. Advanced Performance Materials, 1995. 2(4): p. 349-368.

7. Lütjering, G. and J.C. Williams, Titanium. 2007: Springer.

8. Collings, E., The physical metallurgy of titanium alloys. American Society for Metals, 1984, 1984: p. 261.

9. Emsley, J., Nature’s building blocks: an AZ guide to the elements. 2011: Oxford University Press.

10. Branco, G.A.C., Effect of Thermo-Mechanical Treatment on Texture Evolution of Polycrystalline Alpha Titanium. 2005.

11. Warwick, L.W.J., Texture, Microstructure and Deformation Mechanisms in Titanium Alloys in Department of Materials. 2011: Imperial College London.

12. Leyens, C. and M. Peters, Titanium and titanium alloys: fundamentals and applications. 2003: John Wiley & Sons.

13. Barlat, F., et al., 6 Yield Surface Plasticity and Anisotropy. Stress, 2004. 1: p. 2.

14. Mises, R.v., Mechanik der plastischen Formänderung von Kristallen. ZAMM‐Journal of Applied Mathematics and Mechanics/Zeitschrift für Angewandte Mathematik und Mechanik, 1928. 8(3): p. 161-185.

15. Partridge, P., The crystallography and deformation modes of hexagonal close-packed metals. Metallurgical reviews, 1967. 12(1): p. 169-194.

16. Yoo, M., Slip, twinning, and fracture in hexagonal close-packed metals. Metallurgical Transactions A, 1981. 12(3): p. 409-418.

17. Levine, E.D., Deformation mechanisms in titanium at low temperatures. 1966: p. 1558-1565.

18. Britton, T., F. Dunne, and A. Wilkinson. On the mechanistic basis of deformation at the microscale in hexagonal close-packed metals. in Proc. R. Soc. A. 2015. The Royal Society.

19. Chichili, D., K. Ramesh, and K. Hemker, The high-strain-rate response of alpha-titanium: experiments, deformation mechanisms and modeling. Acta materialia, 1998. 46(3): p. 1025-1043.

20. Zaefferer, S., A study of active deformation systems in titanium alloys: dependence on alloy composition and correlation with deformation texture. Materials Science and Engineering: A, 2003. 344(1): p. 20-30.

21. Graff, S., Micromechanical modeling of the deformation of HCP metals. 2008, GKSS-Forschungszentrum Geesthacht GmbH, Bibliothek/Library.

22. Paufler, P., WF Hosford. The mechanics of crystals and textured polycrystals. Oxford University Press, New York–Oxford 1993. 248 Seiten, Preis£ 30,–. ISBN 0‐19‐507744‐X. Crystal Research and Technology, 1994. 29(4): p. 532-532.

23. Stanford, N., U. Carlson, and M. Barnett, Deformation twinning and the Hall–Petch relation in commercial purity Ti. Metallurgical and Materials Transactions A, 2008. 39(4): p. 934-944.

24. Randle, V. and O. Engler, Introduction to texture analysis: macrotexture, microtexture and orientation mapping. 2000: CRC press.

25. Christian, J.W. and S. Mahajan, Deformation twinning. Progress in materials science, 1995. 39(1-2): p. 1-157.

26. Lainé, S.J. and K.M. Knowles, {11¯ 24} deformation twinning in commercial purity titanium at room temperature. Philosophical Magazine, 2015. 95(20): p. 2153-2166.

27. Chun, Y., et al., Effect of deformation twinning on microstructure and texture evolution during cold rolling of CP-titanium. Materials Science and Engineering: A, 2005. 398(1): p. 209-219.

28. Salem, A.A., S.R. Kalidindi, and R.D. Doherty, Strain hardening of titanium: role of deformation twinning. Acta Materialia, 2003. 51(14): p. 4225-4237.

29. Suwas, S. and R.K. Ray, Crystallographic texture of materials. 2014: Springer-Verlag.

30. Bunge, H., Three-dimensional texture analysis. International Materials Reviews, 1987. 32(1): p. 265-291.

31. Tanabe, A., et al., The formation of hot rolled texture in commercially pure titanium and Ti–6Al–4V alloy sheets. Titanium, 1980. 80: p. 937-945.

32. Grewen, J. Textures of Hexagonal Metals and Alloys and Their Influence on Industrial Application. in Pont-a-Mousson Conference on Texture. 1973.

33. Agnew, S., et al., Study of slip mechanisms in a magnesium alloy by neutron diffraction and modeling. Scripta Materialia, 2003. 48(8): p. 1003-1008.

34. Yang, P., et al. Texture, microstructure and strain sensibility in compressed magnesium alloys. in Materials Science Forum. 2005. Trans Tech Publ.

35. Wang, Y., Fundamentals of Recrystallization in Titanium Alloys, in School of Materials, Faculty of Engineering and Physical Sciences. 2014, University of Manchester: United Kingdom.

36. Gupta, R., C. Mathew, and P. Ramkumar, Strain hardening in aerospace alloys. Frontiers in Aerospace Engineering, 2015.

37. Callister, W.D. and D.G. Rethwisch, Fundamentals of materials science and engineering. Vol. 21. 2013: Wiley New York.

38. Salem, A., S. Kalidindi, and S. Semiatin, Strain hardening due to deformation twinning in α-titanium: Constitutive relations and crystal-plasticity modeling. Acta Materialia, 2005. 53(12): p. 3495-3502.

39. Salem, A.A., et al., Strain hardening due to deformation twinning in α-titanium: mechanisms. Metallurgical and Materials Transactions A, 2006. 37(1): p. 259-268.

40. Salem, A.A., S.R. Kalidindi, and R.D. Doherty, Strain hardening regimes and microstructure evolution during large strain compression of high purity titanium. Scripta Materialia, 2002. 46(6): p. 419-423.

41. Nemat-Nasser, S., W. Guo, and J. Cheng, Mechanical properties and deformation mechanisms of a commercially pure titanium. Acta materialia, 1999. 47(13): p. 3705-3720.

42. Doner, M. and H. Conrad, Deformation mechanisms in commercial Ti (0.5 at. pct oineq) at intermediate and high temperatures (0.3-0.6 tinm). Metallurgical Transactions, 1973. 4(12): p. 2809-2817.

43. Biswas, S. and S. Kailas, Strain rate response and wear of metals. Tribology international, 1997. 30(5): p. 369-375.

44. Sergueeva, A., et al., Advanced mechanical properties of pure titanium with ultrafine grained structure. Scripta Materialia, 2001. 45(7): p. 747-752.

45. Jia, D., et al., Deformation behavior and plastic instabilities of ultrafine-grained titanium. Applied Physics Letters, 2001. 79(5): p. 611-613.

46. Doherty, R., et al., Current issues in recrystallization: A review. Materials Today, 1998. 1(2): p. 14-15.

47. Rollett, A., et al., Recrystallization and related annealing phenomena. 2004: Elsevier.

48. Huang, K. and R. Logé, A review of dynamic recrystallization phenomena in metallic materials. Materials & Design, 2016. 111: p. 548-574.

49. Yu, Q., et al., High-strength titanium alloy nanopillars with stacking faults and enhanced plastic flow. Applied Physics Letters, 2012. 100(6): p. 063109.

50. Ruff, A., Measurement of stacking fault energy from dislocation interactions. Metallurgical and Materials Transactions B, 1970. 1(9): p. 2391-2413.

51. Gallagher, P., The influence of alloying, temperature, and related effects on the stacking fault energy. Metallurgical Transactions, 1970. 1(9): p. 2429-2461.

52. Yang, X.Y., et al. Effect of initial grain size on deformation behavior and dynamic recrystallization of magnesium alloy AZ31. in Materials Science Forum. 2005. Trans Tech Publ.

53. Wu, W., et al., Effect of initial microstructure on the dynamic recrystallization behavior of Mg–Gd–Y–Zr alloy. Materials Science and Engineering: A, 2012. 556: p. 519-525.

54. Zhu, S., et al., Fabrication of Mg Al Zn Mn alloy sheets with homogeneous fine-grained structures using high strain-rate rolling in a wide temperature range. Materials Science and Engineering: A, 2013. 559: p. 765-772.

55. Zhu, S., et al., Effect of twinning and dynamic recrystallization on the high strain rate rolling process. Scripta Materialia, 2010. 63(10): p. 985-988.

56. Zhu, S., et al., Feasibility of high strain-rate rolling of a magnesium alloy across a wide temperature range. Scripta Materialia, 2012. 67(4): p. 404-407.

57. Zhu, S., et al., Mechanisms for enhanced plasticity in magnesium alloys. Acta Materialia, 2015. 82: p. 344-355.