Density Functional Theory and Its Application in Computational Material Science
Info: 4038 words (16 pages) Dissertation
Published: 16th Dec 2019
Tagged: Computer Science
AN INTRODUCTION TO DENSITY FUNCTIONAL THEORY AND ITS APPLICATION IN COMPUTATIONAL MATERIAL SCIENCE
ABSTRACT
Material science is a highly interdisciplinary field. It is dedicated to the understanding of the relations between physical and chemical properties, processes at atomic scale (i.e microscopic and macroscopic), production and engineering applications. In present, the requirement of highly effective materials not only limited to the process variables (mechanical forming and annealing in metallurgy, microstructure study), but in-depth analysis of materials at atomic and subatomic scale. Computational material science is the best method to unravel the hidden structure-property relationship using computational techniques.
Modern many-body computational science involves study of electrons, atoms, molecules, nano-materials and solids. Density functional theory is a computational technique which is used to forecast the properties of molecules and bulk materials. It is a method for inquire the electronic structure of many-body systems and is based on a determination of a given system’s electron density rather than its wave function.
This paper reviews the fundamentals of density functional theory, quantum mechanics and follows the breakthrough in their application. Two examples from material science among many current applications and the future expectation and scope are discussed.
Keywords: DFT, Quantum mechanics, Schrödinger equation, Electron density
1. INTRODUCTION
We are aware that computational technology is a strong partner to the experimental and theoretical studies. It is accelerated by the increasing power of computers and the development of new methods of calculation. Now it is one of the fastest areas of science and engineering. The main attributes of computational material science are atoms, the constituent electrons and nuclei. They follow specific rules, without exception. If
an exception is observed, then it is mainly because of human error. Unlike humans, an electron does not kill itself or another electron because of hate or love. It is the same for atoms, nuclei, molecules and materials. They simply follow the laws of nature, predominantly classic mechanics and quantum mechanics in terms of electromagnetic forces. Therefore, we can predict virtually all forms of phenomena encountered in tracking the electrons, nuclei, atoms and the interactions between these of the material.
The efficient pattern of density function demonstrates that the ground state and other attributes of an electron in an extraneous system can be find out from knowledge of the allocation of the electron density n(r). Fermi et al.[1] and Thomas et al.[2] acknowledged the elemental nature of the electron density and applied to atoms. The density functional approach allows us to determine E(ri) and so the structure related properties, without using experimental input. Figure 1 depicts the remarkable raise in the number of publications on the topics “density functional” and density functional theory “(DFT)” in current years.
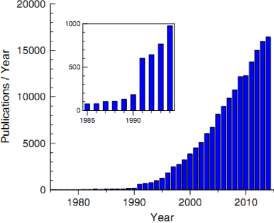
Figure 1: Number of publications per year (1975–2014) on topic DFT. From Jones et al.[3]
The purpose of this article is to highlight the properties and fundamental phenomena of materials and understand how DFT helps to design and build the best materials for the world by modelling materials programmed in computer with theories and physics-based algorithms, mathematics, chemistry, materials science and calculation.
2. BASIC QUANTUM MECHANICS
Four fundamental forces act on matters. Those are probably originated from the Big Bang. Which are the electromagnetic force, the force of gravity and nuclear forces strong and weak acting within atomic nuclei. Materials science interested only the first, because the materials the studies rarely meet the other three forces. The electromagnetic force is the same force of the nuclei and electrons. If a precise description of these interactions is possible, all the properties and phenomena, experimentally relevant, of materials will be found out as a result of our calculations. These laws applicable to such small particles are known as quantum mechanics.
The quantum nature of electrons is suggested by many researchers hidden in their statements. Niels Bohr (1913) has proposed that the electron in hydrogen does not flow on an arbitrary orbit but specific orbitals that the electron does not radiate energy. In these orbitals, it has shown that only specific energies are authorized as
E=-13.6eVn2
(1)
Where n is the number of orbitals. The energies are, of course, negative because they are bound states of a centre nuclei, reference to the zero state energy when they are infinitely separated. It also proposed that electrons can jump to orbits by absorbing and emitting energy. Louis de Broglie (1924) imagined the dual nature of electrons, different and redefined a particle and a wave as a single “wave of the matter.” He said in a surprising statement that the momentum of a particle (P) is inversely proportional to the wavelength (λ) and frequency is directly proportional to the kinetic energy (E) of the particle.
P=hλ
(2)
E=hυ
(3)
Where P is momentum, h is the Planck’s constant, λ is wavelength and
υis frequency. Erwin Schrödinger (1926), allegedly inspired by the Swiss winter and other things, it proposed an equation that belongs to level (or exceeded) of Newton and Einstein. The Schrödinger wave equation is as easy as the following
ĤΨ(ri,RI,t)=EΨ(ri,RI,t)
(4)
Where,
Ĥis Hamiltonian operator,
Ψis wave function and E is system energy. The variables
ri,RI and tare coordinates of electron, nucleus and time respectively. If we do shorten the wave to pinpoint to find its location, then the wave has no momentum to speak. This is a simplified representation of Heisenberg’s uncertainty principle (1927).
3. MANY PARTICLE PROBLEM IN SOLIDS
As stated above, the wave function in quantum mechanics describes the quantum state of a set of particles in an isolated system. An operator is one which does mathematical operation on a single variable or many variables. A quantum mechanical operator is one which is observable in quantum mechanics, like Hamiltonian operator and ground state is the most stable state of the system which posses the lowest energy. By knowing the above basic terms, the many-particle problem in solid is defined as multi body problem which consists of a collection of atoms. It is necessary to find its ground state by solving the Schrödinger equation as bellow.
ĤΨri, RI=EΨri, RI
(5)
Where,
Ĥthe Hamiltonian operator consists of kinetic energy operator
T̂and the coulombic one as explained bellow
Ĥ=T̂+V̂coulomb
(6)
V̂coulomb=qiqjr⃗i-r⃗j
(7)
3.1 Born Oppenheimer approximation
This approximation says that the mass of nuclei is much more large compared to the mass of electron.
mnuclei≫me
(8)
The fair conclusion we can draw from this approximation is the heavy element is much more slower compared to the lighter one. That means we can separate the dynamics of nuclei and electron.
Let the time need by electrons to find the ground state for a fixed set of nuclei is small compared to the nuclei. That is the electrons only see the external potential of static nuclei. So decoupling the wave function will give us
Ψri, RI→ΨNRI*Ψeri,
(9)
3.2 Solution to Schrodinger Equation
For many-particle problem the solution of Schrödinger equation will look as bellow
ĤΨr1,r2,r3,…..rN= EΨr1,r2,r3,…..rN
(10)
The electronic Hamiltonian consists of three terms as in equation (11). The first term from left is the kinetic energy possessed by the electrons. Second term in the middle is the external potential experienced by the interaction of electrons with nuclei and the third term is the electron-electron interaction in the body.
Ĥ=-h22me∑iNe∇i2+∑iNeVextri+∑i=1Ne∑j>1U(ri,rj)
(11)
4. DENSITY FUNCTIONAL THEORY
Density functional theory is derived from first principle method which uses electron density as main variable to solve n-electron problem [4]–[7]. In this method the 3n-dimensional equation (problem) is transferred to n separate 3-dimensional one. This theory suggests that, there is no individual electron. Rather, there is three dimensional density of electrons. Electron density is an observable quantity and independent of number of electrons after it constructed. The important point is that a quantum system is now a problem depending on the electron density. This will significantly reduce the computational effort in practical use of molecules, solids and materials. The DFT description is finally progressed to treat systems containing up to thousands of electrons and allows experiments for materials. These days, the methods were so effective in terms of precision and efficiency that scientists routinely use them in a wide range of disciplines.
4.1 Electron density
In an n-electron quantum system, electron density is the key parameter. The variation of electron density with atomic distance is depicted in Figure 2. It is clear that core electrons are much localised to the nucleus and valence electrons are diffused. It is not easy to define the wave function of electron density. The decoupled form is presented in equation (12).
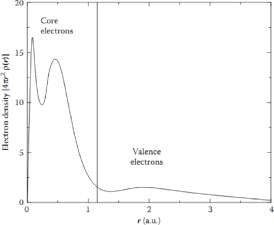
Figure 2: variation of electron density with atomic distance. From [8]
nr= Ψ*r1,r2,r3,…..rN Ψr1,r2,r3,…..rN
(12)
4.2 Hartree method: One-electron model
A method for calculating the wave function of an atom was developed by Hartree [9], [10], who introduced the idea of a “self-consistent field” with particular reference to valence electrons and groups of core electrons. In this approach, the wave function of an electron is determined from the field of the nucleus and the other electrons in a self-consistent fashion. That is the jth electron is treated as a point charge in the field of all other electrons. This simplifies the many-electron problem to many-one electron problem (see Figure 3). The wave function of the N-electron system can be approximated by the product of N single-particle functions
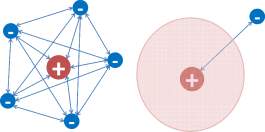
Figure 3: Transformation of many-electron problem to many-one electron problem
Ψr1,r2,r3,…..rN=Ψ1r1*Ψ2r2*…*ΨNrN
(13)
The electron density in terms of individual electron wave function is described as bellow.
nr= 2∑iΨi*rΨir
(14)
4.3 Honenberg-kohn theorems
Two theorems are stated by Honenberg and Kohn to define the ground state of an electronic system.
- The ground state energy E is a unique functional of electron density
E=E[nr]
(15)
- The electron density that minimise the energy of overall functional is true ground state electron density.
E[nr]>E0[n0r]
(16)
Here functional is nothing but the function of functions like
Ff=∫-11fxdx (17)
4.4 Energy functional
Energy functional is the energy associated with the electron density of a system, which can be divided into two parts known and unknown. The known part is the energy functions that we observe in the system generally. It includes kinetic, coulombic and electron-electron interaction energy.
E{Ψi}=EKnown{Ψi}+EXC{Ψi}
(18)
EKnown{Ψi}=-hme∑i∫Ψi*∇2Ψid3r+∫Vrn(r)d3r+e22∬nrn(r’)r-r’d3rd3r’+Eion
(19)
However, the unknown part is the exchange-correlation functional. It includes all quantum mechanical relation of the system. Unfortunately, this exists as a perfect functional and still unknown to us. So, in all DFT calculation it is approximated. Some simplest exchange-correlation functionals used in many calculations are LDA (local density approximation) and GGA (generalised gradient approximation).
4.5 The kohn-sham scheme
The best of DFT is achieved after kohn-sham scheme was developed. To find the ground state, a set of single electron wave functions are need to be solved and these are depend only on three spatial variables as indicated bellow.
-h2m∇2+Vr+VHr+VXC(r)Ψir=∈i(r)Ψi
This scheme also known as self consistent scheme and the steps involved are as follows
Step 1: Guess some electron density n(r)
Step 2: Solve Kohn-Sham equation with n(r) and obtain single electron wave function
Ψi(r)
Step 3: Calculate electron density based on single electron wave function and compare with step 1
Step 4:
- If different electron density is obtained, then update the assumed one in step 1 and redo the calculations
- If identical electron density is obtained, then true ground state is obtained.
4.6 Forces between atoms
Forces on atoms are easily calculated when electron ground state is obtained.
FI=-dEdri=- Ψi∂Ĥ∂riΨi
(21)
By moving along the ionic forces, ionic ground state can be calculated. Then we can displace ions from the ionic ground state and determine the forces on all other ions.
5. CURRENT RESEARCHES AND APPLICATIONS
More number of researches in DFT are based on finding properties of various materials, oxides, composites, nonmaterial and metastable phases. Two density functional simulation results are discussed here briefly that indicate the scale of DF calculation.
(20)
5.1 Hydrothermal growth of metastable phase
With advancement of computers, computational material design is very necessary prior to synthesis of polymorphs and various metastable phases. Recent research work in Daniil et al. [11] presented an outstanding results in predicting the hydrothermal growth of FeS2 pyrite and marcasite by implementing density functional theory. The hydrothermal growth is nothing but the precipitation from the superheated acquous solution. In their work they found a general framework to view hydrothermal growth computationally in a systematic way.
They, first, calculated the bulk energy and structure of pyrite and marcasite by assigning plane wave function in DFT calculation. Then, the ground state, low-energy crystallographic facet of each phase is obtained by minimising the interfacial energy between the FeS2 solid and water. Finally, the enthalpy of adsorbing dilute H3O+ and OH– ions for each solvated facet is calculated. Surface energy influences the phase selection in FeS2 synthesis. It can be viewed from thermodynamic as well as kinetic perspective. By combining the bulk and surface energy of pyrite and marcasite for all sizes and pH values, they construct the size–pH phase diagram of FeS2, as given in Figure 4.
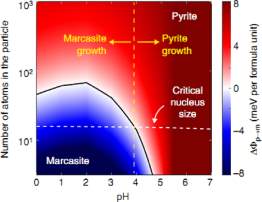
Figure 4: Thermodynamics of nanoscale FeS2. The finite-size phase diagram of FeS2 across a range of pH values. From Daniil et al.
5.2 Modelling of nano structure photoemission test
It is very difficult to analyze the data of the angle of the electronic structure photoemission due to the atomic structure and the influence of the experimental structure on quantum mechanical effects during the measurement. However, it has been simulated the Angle-resolved photoemission spectroscopy (ARPES) of nanoscale molecules to confirm the interpretation of experimental results [12].
Applying the approximation of independent atomic center and based on the calculations of the density functional theory (DFT), they calculated the intensity of photoelectrons in experimental configurations for each given in atomic orbit polyaromatic hydrocarbons of different sizes and a black phosphorus molecule. The initial state is calculated by the density functional theory (DFT) and the initial state is used to explain the ARPES results using a state of plane wave approximation and a formalism of the Fourier transform. Energy levels and molecular orbital wave functions are obtained using DFT calculations. Molecular orbitals are used to calculate the intensity of the emission light of the whole molecule. Emission of light of the whole molecule should be the sum of emissions of its constituent atoms.
In the first place, they have modeled the atomic positions of a molecule in Cartesian coordinates. Then, using this structure, they performed DFT calculations, including geometry optimization. The results of ARPES simulation with experiment is compared as in Figure 5. It simply signifies that DFT is an essential tool in computational material science.
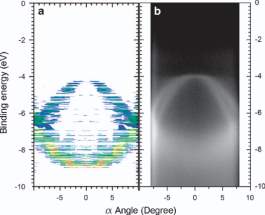
Figure 5: Comparison between simulation and experiment. (a) Simulation, (b) Experimental
6. CONCLUSIONS
In this review, an attempt has been made to introduce the basic fundamentals of density functional theory (DFT) for a many body problem of solids and challenges of DFT in finding perfect exchange correlation functional approximation and is highlighted. However, some recent findings, applications and its importance, such as hydrothermal growth of metastable phase and modelling of nano structure photoemission are explained. I believe that DFT itself is a very powerful tool in modern science and engineering and its shortcomings and challenges will be addressed quickly in near future.
7. REFERENCE
[1] E. Fermi, “Statistical method to determine some properties of atoms,” Rend. Accad. Naz. Lincei, vol. 6, no. December, pp. 602–607, 1927.
[2] L. H. Thomas, “The calculation of atomic fields,” Math. Proc. Cambridge Philos. Soc., vol. 23, no. 5, pp. 542–548, 1927.
[3] R. O. Jones, “Density functional theory: Its origins, rise to prominence, and future,” Rev. Mod. Phys., vol. 87, no. 3, 2015.
[4] U. von Barth, “Basic density-functional theory—an overview,” Phys. Scr., pp. 9–39, 2004.
[5] C. Amador, J. Keller, and J. L. Gázquez, “Density functional theory,” Lect. notes Phys. ; 187, p. 301 p., 1983.
[6] E. S. Kryachko and E. V. Lude??a, “Density functional theory: Foundations reviewed,” Phys. Rep., vol. 544, no. 2, 2014.
[7] K. Capelle, “A Bird’s-Eye View of Density-Functional Theory,” Braz. J. Phys., vol. 36, no. 4a, pp. 1318–1343, 2006.
[8] J. Lee, Computational materials science: an introduction, Second edi. CRC Press, 2016.
[9] D. R. Hartree, “The Wave Mechanics of an Atom with a Non?Coulomb Central Field. Part I. Theory and Methods,” Math. Proc. Cambridge Philos. Soc., vol. 24, no. 3, p. 426, 1928.
[10] D. R. Hartree, “The Wave Mechanics of an Atom with a Non-Coulomb Central Field. Part II. Some Results and Discussion.,” Math. Proc. Cambridge Philos. Soc., vol. 24, no. 3, p. 426, 1928.
[11] D. A. Kitchaev and G. Ceder, “Evaluating structure selection in the hydrothermal growth of FeS2 pyrite and marcasite,” Nat. Commun., vol. 7, pp. 1–7, 2016.
[12] S. H. Park and S. Kwon, “Modeling angle-resolved photoemission of graphene and black phosphorus nano structures,” Sci. Data, vol. 3, p. 160031, 2016.
8. APPENDIX
| 1. | Ĥ | : | Hamiltonian Operator |
| 2. | E | : | Energy of state |
| 3. | Ψri, RI | : | Wave function of quantum system |
| 4. | ri,rj | : | Spatial coordinate of electron |
| 5. | RI | : | Spatial coordinate of nucleous |
| 6. | T̂ | : | Kinetic energy operator |
| 7. | V̂coulomb | : | Coulombic potential |
| 8. | qi,qj | : | Charge of particles |
| 9. | mnuclei,me | : | Mass of nucleus and electron respectively |
| 10. | ΨNRI,Ψeri, | : | Wave function of nucleus and electron respectively |
| 11. | h | : | Plank’s constant |
| 12. | Ne | : | Number of electron |
| 13. | Vext | : | External potential |
| 14. | U(ri,rj) | : | Electron-electron interaction potential |
| 15. | nr | : | Electron density |
| 16. | E0,n0 | : | Ground state energy and electron density |
| 17. | EKnown{Ψi} | : | Unknown energy functional |
| 18. | EXC{Ψi} | : | Exchange correlation function |
| 19. | Eion | : | Potential energy between positive nuclei |
| 20. | Vr | : | Coulombic potential |
| 21. | VHr | : | Many-one electron potential |
| 22. | ∈i(r)Ψi | : | Ground state wave function |
| 23. | FI | : | Atomic force at ground state |
Kohn-Sham scheme Flow chart:


Replace n(r) by n(r)Step 3
Guess n(r)
Solve Kohn-Sham Scheme
-h2m∇2+Vr+VHr+VXC(r)Ψir=∈i(r)Ψi
with n(r)
to obtain single electron wave function
Ψ1r


Calculate electron density
nr= 2∑iΨi*rΨir
based on single electron wave function
Compare n(r)Step 3
with
assumed n(r)Step 1.
Is it different?
No
Yes
True ground state is obtained
Cite This Work
To export a reference to this article please select a referencing stye below:
Related Services
View allRelated Content
All TagsContent relating to: "Computer Science"
Computer science is the study of computer systems, computing technologies, data, data structures and algorithms. Computer science provides essential skills and knowledge for a wide range of computing and computer-related professions.
Related Articles
DMCA / Removal Request
If you are the original writer of this dissertation and no longer wish to have your work published on the UKDiss.com website then please:




