Thermal effects on vibration and stability of functionally graded cylindrical shells surrounded by Pasternak elastic foundation

Abstract

Vibration and stability analyses of functionally graded cylindrical shells surrounded by elastic foundation under axial and thermal loads are investigated in this paper. Using Hamilton’s principle, governing equations are derived based on first-order shear deformation theory (FSDT) assumptions and Sanders-Koiter formulation. Galerkin’s method is implemented to achieve the relevant expressions for frequency parameters and critical axial/thermal loads. Emphasis is placed on the solution method to derive a more accurate heat conduction equation through the shell thickness. The following two solution methods are considered: analytical exact solution and polynomial series solution. In some cases the latter solution method that has extensive application is observed to have some significant effects on the results, especially on the stability characteristics. A comprehensive validation of the results also has been provided.

Keywords: FG cylindrical shell; Vibration and stability; Axial and thermal loads; Pasternak Elastic Foundation.

1. Introduction

The use of functionally graded materials (FGMs) in various applications has increased in recent years. The idea of FGMs was first introduced by a team of Japanese scientists in 1984 [1]. FGMs are a form of composite materials that are designed to have desired properties for specific applications. FGMs are considered as a solution for the aerospace industries where high temperature resistance and lightweight but stiff structures need to be provided. These new materials with excellent thermo-mechanical properties are resistant to high temperatures. Functionally graded (FG) cylindrical shells also have extensive applications in different engineering structures, such as aerospace, pressure vessels and pipes, chemical plants, etc.

Among the various researches on FGMs, one of the most interesting issues is to analyze the vibration and stability behaviors of shells. Analytical study of the shells predicts the necessary mechanical measures to avoid the expected damage to the system and ensures its safety and stability. Many studies have been reported on the vibration and stability of FG cylindrical shells (Loy et al. [2], Pradhan et al. [3], Najafizadeh and Isvandzibaei [4, 5], Matsunaga [6], Tornabene [7], Huang et al. [8], Malekzadeh and Heydarpour [9], Ebrahimi and Sepiani [10] and Naeem et al. [11]). Isvandzibaei et al. [12] investigated vibration behavior of FGM cylindrical shells including internal pressure and ring support effects based on Love-Kirchhoff theory with various boundary conditions. Mechanical buckling analysis of moderately thick FG cylindrical panels subjected to axial compression for combinations of clamped and simply supported boundary conditions is considered by Golmakani et al. [13]. Hadi et al. [14] studied free vibration characteristics of FGM cylindrical shells surrounded by elastic medium under axial force, lateral pressure and different boundary conditions using wave propagation method.

Free vibration analysis of simply supported FG cylindrical shells in thermal environment based on Love’s thin shell theory was performed by Haddadpour et al. [15]. Pradyumna et al. [16] investigated free vibration and buckling behavior of singly and doubly curved FG shell panels in thermal environments. Thermal buckling loads of cylindrical shells of functionally graded materials were investigated by Shahsiah and Eslami [17]. Sheng and Wang [18] investigated the effect of thermal load on the vibration, buckling and dynamic stability of FG cylindrical shells embedded in a linear elastic medium, based on the first-order shear deformation theory (FSDT) considering the rotary inertia and transverse shear strains. The postbuckling response of an FG cylindrical shell of finite length, embedded by a Pasternak-type elastic medium and subjected to lateral pressure in thermal condition was carried out by Shen et al. [19]. Shah et al. [20] studied vibrations of FG cylindrical shells based on Winkler and Pasternak-type elastic foundations. Stress analysis of a rotating disk made of FGMs by using finite element method (FEM) and considering the effect of thickness variation and dependency of material properties to temperature distribution is conducted by Damircheli and Azadi [21]. Bagherizadeh et al. [22, 23] studied the mechanical and thermal buckling behavior of FG cylindrical shells surrounded by Pasternak elastic foundation. Ovesy and Fazilati [24] performed parametric instability analysis of moderately thick FG cylindrical panels using finite strip methods (FSM). They used Reddy-type third order shear deformation theory (HSDT) and two versions of FSM, namely semi-analytical and B-spline methods, were developed. Ovesy et al. [25] used semi-analytical finite strip method for analyzing the post-buckling behavior of FG rectangular plates in thermal environments where plates are under uniform, tent-like or nonlinear temperature change through the thickness. Nonlinear transient heat conduction analysis for hollow thick temperature-dependent 2D-FGM cylinders subjected to transient non-uniform axisymmetric thermal loads is developed by Shojaeefard and Najibi [26].

In the aforementioned thermal studies and many others, the thermal loads may be simulated in three types: (1) uniform temperature rise; (2) linear temperature change through the thickness; (3) nonlinear temperature change through the shell thickness when the temperature distribution is governed by the steady state heat conduction equation. In the third case, many researchers assume a solution in the form of a power series, but no attention is paid to the possible drawback of this solution method. To the best of authors’ knowledge, the vibration and stability analyses of FG cylindrical shells surrounded by an elastic medium under thermo-mechanical loads for which the nonlinear temperature distribution through the shell thickness are obtained by different approaches, are not reported elsewhere. Thus, the latter task is fulfilled in the current paper. The material properties of the FGM including Young’s modulus, Poisson’s ratio, density, thermal expansion coefficient and thermal conductivity are assumed to be variable according to a power law function through the thickness coordinate. The Pasternak model is used to describe the reaction of the elastic foundation on the cylindrical shell. Governing equations based on the FSDT of Sanders-Koiter for the cylindrical shells are derived. The boundary condition is considered to be simply-supported. The governing equations are solved by using the Galerkin’s method. The results of this study are compared with the available results in the literature, wherever possible. Based on the validated results, the emphasis is partially placed on the solution method to achieve a more accurate heat conduction equation through the shell thickness. Comparing the results with exact analytical solution, it is observed that in some cases the series approach for temperature distribution through the shell thickness has a significant effect on the results, especially on the stability characteristics and it can lead to predict inaccurate results.

2. Theoretical aspects

Consider a circular cylindrical shell whose constant thickness, radius and axial length are denoted by h, R and L, respectively (see Fig. 1). The present study considers functionally graded material composed of two materials. Suppose that a typical material property P(z) is varied along the shell thickness according to the following expressions (a power law):

Pz=Po-PiVo+Pi,         Vo=z+0.5hhN,  0≤N≤∞,   -h/2≤z≤h/2

where

Po and Pi denote the property at the outer and inner surfaces of the shell, respectively; and N expresses the volume fraction exponent. Here we assume that elastic modulus

E, mass density

ρ, Poisson’s ratio

υ, thermal expansion

α, and thermal conductivity

k vary according to Eq. (1).

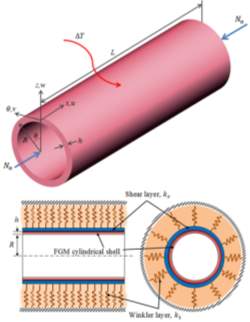
Fig. 1. The FG cylindrical shell on Pasternak elastic foundation under axial and thermal loads.

Based on the first order shear deformation theory, the displacements of any arbitrary point in the shell thickness could be expressed as:

U=ux,θ,t+zψxx,θ,t ,   V=vx,θ,t+zψθx,θ,t , W=wx,θ,t

where u, v and w are the midplane displacement components along the x, θ and z directions, respectively; and ψx and ψθ denote rotations about the θ and x axes, respectively, of corresponding point on the midplane (i.e. z = 0).

The strains associated with the displacement field (2) can be expressed as:

εxx=εx,0+zkx ,   εθθ=εθ,0+zkθ ,   γxθ=γxθ,0+zkxθ ,   γxz=γxz,0 ,   γθz=γθz,0

where εi,0(i=x,θ) and γi,0(i=xθ,xz,θz) are normal and shear strains of the midplane and ki(i=x,θ,xθ) denote the midplane curvatures. Relations between midplane strains, curvatures and displacements (kinematics relations) based on the Sanders-Koiter FSDT are as follows [27]:

εx,0=∂u∂x ,   εθ,0=∂vR∂θ+wR , γxθ,0=∂uR∂θ+∂v∂x ,   γxz,0=ψx+∂w∂x , γθz,0=ψθ+∂wR∂θ-vR , kx=∂ψx∂x ,   kθ=∂ψθR∂θ , kxθ=∂ψxR∂θ+∂ψθ∂x+12R∂v∂x-∂uR∂θ

Considering the thermal effects, constitutive relations are given by:

NxxNθθNxθMxxMθθMxθ=A11   A12   0   B11   B12   0A12  A22    0   B12   B22   00      0     A66  0      0     B66B11   B12   0   D11   D12   0B12  B22    0   D12   D22   00      0     B66  0      0     D66εx,0εθ,0γxθ,0kxkθkxθ-NxxNθθNxθMxxMθθMxθth QxQθ=C4400C55γxz,0γθz,0

where Aij,Bij,Dij and Cii are the extensional, coupling, bending, and shear stiffness, respectively and are defiend as:

Aij,Bij,Dij=∫-h2h2Qij1,z,z2dz , i,j=1,2,6 Cii=∫-h2h2Qiidz , i=4,5 Q11=Q22=Ez1-υ2z ,   Q12=υzEz1-υ2z , Q66=Ez21+υz ,   Q44=Q55=KEz21+υz

E(z) is Young’s modulus, υ(z) is Poisson’s ratio and K is the shear correction factor chosen equal to 5/6 [28] and thermal stresses and moments resultants are defined as:

NxxNθθNxθMxxMθθMxθth=∫-h2h2Q11+Q12Q12+Q220Q11+Q12zQ12+Q22z0αz∆Tzdz ,   ∆Tz=Tz-Ti

α(z)

is the thermal expansion coefficient of the FGM cylindrical shell. According to Eq. (6), it is seen that A11=A22, B11=B22, D11=D22 and C44=C55.

ΔT(z) is the temperature change relative to the stress free state, and the inner surface temperature

Ti is assumed to be the initial temperature. The thermal stress is zero at T(z)=Ti.

The temperature distribution through the thickness is obtained by solving the steady-state heat conduction equation through the thickness of the FG cylindrical shell. The equation for the temperature field through the thickness is given by [28]:

ddzk(z)dTdz=0

where the thermal conductivity

k(z) of the FG cylindrical shell is assumed to vary according to power law. Eq. (8) is solved by imposing the boundary conditions

T(-h/2)=Ti and T(h/2)=To. The solution of this equation, obtained from polynomial series, gives [29, 30]:

Tz=Ti+(To-Ti)η(z)

where:

ηz=1C2z+h2h-koiN+1ki2z+h2hN+1+koi22N+1ki22z+h2h2N+1-koi33N+1ki32z+h2h3N+1+koi44N+1ki42z+h2h4N+1-koi55N+1ki52z+h2h5N+1
C=1-koiN+1ki+koi22N+1ki2-koi33N+1ki3+koi44N+1ki4-koi55N+1ki5
koi=ko-ki

In this study, the analytical solution of the heat conduction equation is also considered and the effect of this approach on the results is investigated. Temperature distribution across the shell thickness can be calculated analytically by considering boundary conditions and integrating the heat conduction equation as:

Tz=Ti+(To-Ti)∫-h/2h/2dzk(z)∫-h/2zdzk(z)

By definition:

NT=Nxx  Nθθ  Nxθ  Mxx  Mθθ  Mxθ  Qx  Qθ   eT=εx,0  εθ,0  γxθ,0  kx  kθ  kxθ  γxz,0  γθz,0

The total strain energy of a cylindrical shell embedded in an elastic medium can be written as:

U=12∫0L∫02π NTeRdθdx+12∫0L∫02πk1w2+ks∂w∂x2+ks∂wR∂θ2Rdθdx

where the second part of the above equation is related to the elastic foundation energy which is added to the strain energy of the shell.

k1, in force per unit volume, is the Winkler-foundation parameter, and ks, in moment per unit area, is the shear parameter of a Pasternak type of foundation.

Considering all inertia terms including the rotary inertia, the kinetic energy of a cylindrical shell is defined as:

T=12∫0L∫02πI1∂u∂t2+∂v∂t2+∂w∂t2+2I2∂u∂t∂ψx∂t+∂v∂t∂ψθ∂t+I3∂ψx∂t2+∂ψθ∂t2Rdθdx

where inertia terms

I1,

I2 and

I3 are defined as:

I1=∫-h/2h/2ρzdz,     I2=∫-h/2h/2ρzzdz,   I3=∫-h/2h/2ρzz2dz

The work done by compressive force Na and thermal force Nxxth can be calculated by [17, 31]:

W=12∫0L∫02π(Na-Nxxth)∂v∂x2+∂w∂x2Rdθdx

Using Eqs. (15), (16) and (18) into Hamilton’s principle and performing lengthy mathematical manipulating, the governing equations of the cylindrical shell embedded in an elastic medium under thermo-mechanical loads can be expressed as:

∂Nxx∂x+1R∂Nxθ∂θ-12R2∂Mxθ∂θ-I1∂2u∂t2-I2∂2ψx∂t2=0
∂Nxθ∂x+1R∂Nθθ∂θ+12R∂Mxθ∂x+1RQθ+Na-Nxxth∂2v∂x2-I1∂2v∂t2-I2∂2ψθ∂t2=0
-1RNθθ+∂Qx∂x+1R∂Qθ∂θ+Na-Nxxth∂2w∂x2-k1w+ks∂2w∂x2+1R2∂2w∂θ2-I1∂2w∂t2=0
∂Mxx∂x+1R∂Mxθ∂θ-Qx-I2∂2u∂t2-I3∂2ψx∂t2=0
∂Mxθ∂x+1R∂Mθθ∂θ-Qθ-I2∂2v∂t2-I3∂2ψθ∂t2=0

After substituting Eqs. (5) and (4) into Eqs. (19-23), the shell equations of motion can be expressed in terms of the middle surface displacement components u, v,w, ψx, ψθ.

3. Method of solution

For the present study, only simply supported boundary condition at x=0 and x=L would be considered. A solution for the motion equations, satisfying boundary condition, can be described by:

u=Acosλxcosnθcos⁡ωt v=Bsinλxsinnθcos⁡ωt w=Csinλxcosnθcos⁡(ωt) ψx=Dcosλxcosnθcos⁡ωt ψθ=Esinλxsinnθcos⁡(ωt)

where λ=mπ/L;

A, B, C, D and E are the constants denoting the amplitudes of vibration; m and n are the axial and circumferential wave numbers, and ω(rad/s) is the natural angular frequency of the vibration.

Substituting the displacements model into Eqs. (19-23) and application of Galerkin’s method, a set of equations is revealed as follows:

T11T12T13T14T15T21T22T23T24T25T31T32T33T34T35T41T42T43T44T45T51T52T53T54T55ABCDE=0

where T_ij are some coefficients in which Na, Nxxth and ω have appeared (see Appendix A).

Eq. (25) is solved for natural frequencies and buckling loads (mechanical or thermal) of the shell by imposing the condition of non-trivial solutions and equating the characteristic determinant [Tij] to zero.

4. Numerical results and discussion

Some examples are provided to show the validity of the present study. The first verification is performed for a simply supported cylindrical shell surrounded by an elastic medium. The comparison is shown Fig. 2. It should be noted that Shah et al. [20] results are based on Love’s thin shell theories. It is observed that the present results are in excellent agreement with those in the literature.

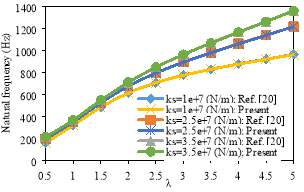
Fig. 2. Variation of natural frequencies of a simply supported FG cylindrical shell; Pasternak foundation (λ=mπ/L, n=1, k₁=1e+7 N/m³, L/R=20, h/R=0.002, E_o=2.07788×10¹¹ Pa,υ_o=0.317756,ρ_o=8166 kg/m³, E_i=2.05098×10¹¹ Pa,υ_i=0.31,ρ_i=8900 kg/m³, N=5).

The second comparison is concerned with the study of mechanical buckling load of a simply supported cylindrical shell. Results for an isotropic cylindrical shell are compared with Batdorf [32] and Ovesy and Fazilati [33] in Table 1 for axial loading. The good agreement between these results shows the high accuracy of the present work. It is seen from Table 1, in case of the lowest radius to thickness ratio (R/h=30) there is a small difference between the present results and those reported by the others. This might have occurred due to the different theories which are used in different studies. Ovesy and Fazilati [33] have used thin shell theory whereas FSDT is used in the current study.

Table 1. Buckling stresses (GPa) for various radius to thickness ratio (m=3, n=0, R=0.3 m, L=0.25 m, E=260 GPa, υ=0.3)

Method	R/h=30	R/h=100	R/h=300
Batdorf’s Theory [32]	5.42	2.34	2.07
Ovesy and Fazilati [33]	5.41	2.34	2.07
Present	5.28	2.34	2.07

Having validated the developed formulation in cases of free vibration (elastically supported or not), mechanical buckling load and thermal buckling temperature (uniform temperature rise), it is now time to focus on the case of non-uniform temperature distribution and investigating the effects of different methods for solving the heat conduction equation. As mentioned earlier in this paper, two different methods are applied to calculate temperature distribution through the shell thickness (series and analytical solutions). For this reason different FG plates are considered. The FG plates have metal on their inner surface and ceramic on their outer surface. The effective thermal conductivities for selected FGMs, calculated at 300 K, are listed in Table 2. It is considered that metal and ceramic surface temperatures are held in 300 K and 800 K, respectively.

Table 2. Thermal conductivities for selected FGMs

Material	Thermal conductivity (W/mK)
Al//Zro2	204/2.09
Al/Al2O3	204/10.4
Ti-6Al-4V/Zro2	6.1/2.09
Si3N4/SUS304	10.12/12.143

Fig. 3 shows temperature distribution through the thickness of the considered FG plates based on the two above mentioned approaches, for different values of volume fraction exponents. It could be concluded from the graphs that the results of two approaches are different based on the FG configuration. In case of FG plates with materials in which thermal conductivities are close to each other (for example Si3N4/SUS304) there is a little difference between two methods, as expected for isotropic plate. Difference between two methods is decreased as difference between thermal conductivities of two constituent materials is decreased. It should be noted that, in the series approach, even by taking the first fourteen terms of series, the results are still surprisingly different from those obtained by the exact analytical solution. Ovesy et al. [25] have also reported that the results of polynomial series were different from those obtained from the analytical exact solution. Based on the obtained results it could be concluded that the series method may be applicable with sufficient accuracy for composition in which thermal conductivities of materials be close to each other.

 

 

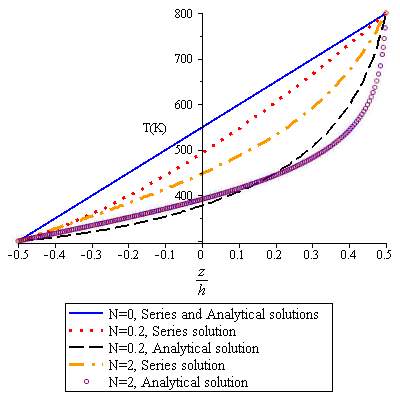
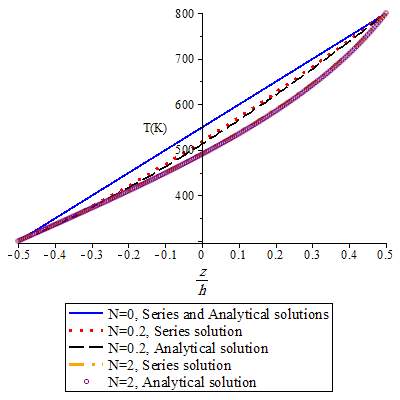
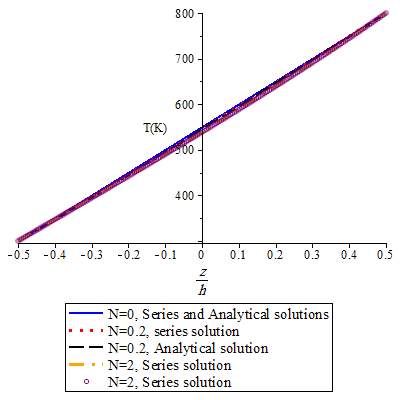
Fig. 3. Temperature distribution through the thickness for a) Al/Zro2, b) Al/Al2O3, c) Ti-6Al-4V/Zro2 and d) Si3N4/SUS304.

Based on the two temperature distributions, vibration and stability behavior of FG simply-supported cylindrical shells will be studied and effects of the two different approaches on the results will be investigated. Consider a FG cylindrical shell with the following parameters (Aluminum and Zirconia are used in the inner and outer surfaces of the shell, respectively); Aluminum: E_i=70 GPa,υ_i=0.3,ρ_i=2707 kg/m³, k_i=204 W/mK, α_i=23×10^-6 1/^◦C and Zirconia: E_o=151 GPa,υ_o=0.3,ρ_o=3000 kg/m³, k_o=2.09 W/mK, α_o=10×10^-6 1/^◦C.

The following buckling load of the shell as suggested by Timoshenko and Gere [34] and non-dimensional elastic foundation parameters are used in numerical results:

Ncr=Emh2R31-υm2 , Kn1=k1R21-υm2Emh ,   Kns=ks1-υm2Emh

where Em and υm are elastic modulus and Poisson’s ratio of the metal material respectively.

Fig. 4 shows the effects of thermal load on non-dimensional fundamental frequency

Ω (Ω2=ω2R21-υm2ρm/Em; ω denotes the fundamental frequency) for different non-dimensional medium modulus parameters Kn1 and Kns. It is noted that the cylinder is subjected to an axial load of Na=0.5 Ncr. It is concluded from Fig. 4 that the non-dimensional fundamental frequency decreases as the temperature difference between the inner and outer surfaces increases. The effects of elastic medium parameters and different approaches for temperature distribution on the non-dimensional fundamental frequency are clearly demonstrated in the figures. Considering series solution instead of the analytical solution for temperature distribution leads to a smaller drop in frequency when temperature difference between the inner and outer surfaces increases.

Fig. 5 shows the effects of thermal load on critical axial load (Nacr/Ncr) of a simply supported FG cylindrical shell for different non-dimensional elastic foundation modulus parameters Kn1 and Kns. As seen in Fig. 6, the critical axial load of the FG cylindrical shell decreases linearly as the temperature difference between the inner and outer surfaces increases, and the critical axial load increases as the medium modulus parameters increases. It is also observed that different approaches for temperature distribution have a significant effect on critical axial load.

a)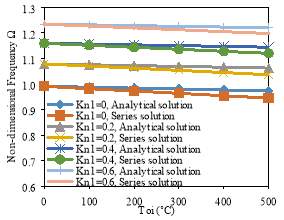 

b)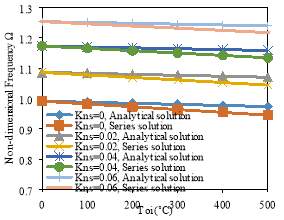

Fig. 4. Non-dimensional fundamental frequency (Ω) variation with temperature difference between the inner and outer surfaces (T_oi) and elastic foundation, m=n=1, N_a=0.5N_cr, L/R=1, h/R=0.01, N=2; a) Winkler parameter and b) shear parameter.

a) 

b)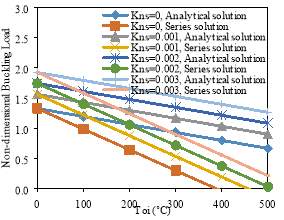

Fig. 5. Non-dimensional buckling load (N_acr/N_cr) variation with temperature difference between the inner and outer surfaces (T_oi) and elastic foundation, m=n=1, N_a=0.5N_cr, L/R=1, h/R=0.01, N=2; a) Winkler parameter and b) shear parameter.

From Figs. 4 and 5 it can be stated that the effect of different approaches for calculation of temperature distribution is more significant for critical axial load than for fundamental frequency. Moreover, the more the effects of shear parameter with respect to Winkler parameter on non-dimensional fundamental frequency and critical axial load are concluded from the graphs.

5. Conclusions

This paper reports the effects of mechanical and thermal loads on the vibration and stability of FG cylindrical shells embedded in an elastic medium, using two methods for through-the-thickness temperature distribution. Based on the first-order shear deformation theory of Sanders-Koiter and application of Hamilton’s principle, a system of equations is derived. Solution of these equations for a simply supported FG cylindrical shell which uses a power law distribution across the thickness coordinate is attempted by using Galerkin’s method. Extensive validation studies are performed for different cases of the problem. Having validated the developed methodology, the effects of two different solution approaches for heat conduction equation through the shell thickness on vibration and stability characteristics of FG cylindrical shells surrounded by an elastic medium under mechanical and thermal loads are then investigated: (i) polynomial series; (ii) analytical solution. The main conclusions are outlined below:

1. Based on the FG configuration and composition, significant differences between temperature distributions through the thickness of the FG plates/shells calculated by polynomials series and exact analytical approaches may be exist, especially for higher values of volume fraction exponents (N).
2. Based on the obtained results and also the popularity of polynomials series approach usage by many researchers, it can be noted that the series method may be applicable with sufficient accuracy in case of FG composition in which thermal conductivities of the materials be close to each other.
3. The natural frequency of the considered FG cylindrical shell embedded in an elastic medium decreases as the temperature difference between the inner and outer surfaces increases, especially in the case of temperature distribution calculated by polynomials series.
4. The natural frequency increases as the Winkler/shear modulus parameters of surrounding medium increases.
5. The critical axial load of the considered FG cylindrical shell decreases linearly as the temperature difference between the inner and outer surfaces increases, especially with a dramatic drop for the case of temperature distribution calculated by polynomials series method.
6. The critical axial load increases as the Winkler/shear modulus parameters of the surrounding medium increases.
7. Shear parameter of elastic foundation has more effects on the non-dimensional fundamental frequency and the critical axial load than Winkler parameter.

Appendix A

T11=A11m2π2L2+A66-B66R+D664R2n2R2-I1ω2 ,   T12=T21=-A12+A66-D664R2mnπLR

T13=T31=-A12mπLR ,   T14=T41=B11m2π2L2+B66-D662Rn2R2-I2ω2

T15=T51=-B12+B66-D662RmnπLR ,   T22=A22n2+C551R2+A66+B66R+D664R2m2π2L2-I1ω2

T23=T32=A22+C55nR2 ,   T24=T42=-B12+B66+D662RmnπLR

T25=T52=B22n2R2+B66+D662Rm2π2L2-C55R-I2ω2

T33=A22+C55n2+ksn21R2+C44+Na-Nxxth+ksm2π2L2+k1-I1ω2

T34=T43=-B12R+C44mπL ,   T35=T53=B22R-C55nR

T44=D11m2π2L2+D66n2R2+C44-I3ω2 ,   T45=T54=-D12+D66mnπLR

T55=D22n2R2+D66m2π2L2+C55-I3ω2

References

[1] M. Koizumi, The concept of FGM, ceramic transactions, Funct. Grad. Mater, Vol. 34, pp. 3-10, 1993.

[2] C. T. Loy, K. Y. Lam, J. N. Reddy, Vibration of functionally graded cylindrical shells, International Journal of Mechanical Sciences, Vol. 41, pp. 309-324, 1999.

[3] S. C. Pradhan, C. T. Loy, K. Y. Lam, J. N. Reddy, Vibration characteristics of functionally graded cylindrical shells under various boundary conditions, Applied Acoustics, Vol. 61, pp. 111-129, 2000.

[4] M. M. Najafizadeh, M. R. Isvandzibaei, Vibration of functionally graded cylindrical shells based on higher order shear deformation plate theory with ring support, Acta Mechanica, Vol. 191, pp. 75-91, 2007.

[5] M. Najafizadeh, M. R. Isvandzibaei, Vibration of functionally graded cylindrical shells based on different shear deformation shell theories with ring support under various boundary conditions, Journal of Mechanical Science and Technology, Vol. 23, No. 8, pp. 2072-2084, 2009.

[6] H. Matsunaga, Free vibration and stability of functionally graded circular cylindrical shells according to a 2D higher-order deformation theory, Composite Structures, Vol. 88, pp. 519–531, 2009.

[7] F. Tornabene, Free vibration analysis of functionally graded conical, cylindrical shell and annular plate structures with a four-parameter power-law distribution, Computer Methods in Applied Mechanics and Engineering, Vol. 198, pp. 2911–2935, 2009.

[8] H. Huang, Q. Han, N. Feng, X. Fan, Buckling of Functionally Graded Cylindrical Shells under Combined Loads, Mechanics of Advanced Materials and Structures, Vol. 18, pp. 337–346, 2011.

[9] P. Malekzadeh, Y. Heydarpour, Free vibration analysis of rotating functionally graded cylindrical shells in thermal environment, Composite Structures, Vol. 94, pp. 2971–2981, 2012.

[10] F. Ebrahimi, H. Sepiani, Transverse shear and rotary inertia effects on the stability analysis of functionally graded shells under combined static and periodic axial loadings, Journal of Mechanical Science and Technology, Vol. 24, No. 12, pp. 2359-2366, 2010.

[11] M. N. Naeem, M. Gamkhar, S. H. Arshad, A. G. Shah, Vibration analysis of submerged thin FGM cylindrical shells, Journal of Mechanical Science and Technology, Vol. 27, No. 3, pp. 649-656, 2013.

[12] M. Isvandzibaei, H. Jamaluddin, R. R. Hamzah, Analysis of the vibration behavior of FGM cylindrical shells including internal pressure and ring support effects based on Love-Kirchhoff theory with various boundary conditions, Journal of Mechanical Science and Technology, Vol. 28, No. 7, pp. 2759-2768, 2014.

[13] M. Golmakani, M. S. Far, M. Moravej, Dynamic relaxation method for nonlinear buckling analysis of moderately thick FG cylindrical panels with various boundary conditions, Journal of Mechanical Science and Technology, Vol. 30, No. 12, pp. 5565-5575, 2016.

[14] A. Hadi, S. Shakhesi, H. R. Ovesy, J. Fazilati, Free Vibration of FGM Cylindrical Shells on Elastic Foundation under Axial force, Lateral Pressure and Different Boundary Conditions, Amirkabir Journal of Mechanical Engineering, Vol. In Press, Accepted Manuscript, Available Online 17 May 2017.

[15] H. Haddadpour, S. Mahmoudkhani, H. Navazi, Free vibration analysis of functionally graded cylindrical shells including thermal effects, Thin-walled structures, Vol. 45, No. 6, pp. 591-599, 2007.

[16] S. Pradyumna, J. Bandyopadhyay, Free vibration and buckling of functionally graded shell panels in thermal environments, International Journal of Structural Stability and Dynamics, Vol. 10, No. 05, pp. 1031-1053, 2010.

[17] R. Shahsiah, M. R. Eslami, Thermal buckling of functionally graded cylindrical shell, Journal of Thermal Stresses, Vol. 26, pp. 277–294, 2003.

[18] G. G. Sheng, X. Wang, Thermal vibration, buckling and dynamic stability of functionally graded cylindrical shells embedded in an elastic medium, Journal of Reinforced Plastics and Composites, Vol. 27, No. 2, pp. 117–134, 2008.

[19] H.-S. Shen, J. Yang, S. Kitipornchai, Postbuckling of internal pressure loaded FGM cylindrical shells surrounded by an elastic medium, European Journal of Mechanics-A:Solids, Vol. 29, pp. 448–460, 2010.

[20] A. G. Shah, T. Mahmood, M. N. Naeem, Z. Iqbal, S. H. Arshad, Vibrations of functionally graded cylindrical shells based on elastic foundations, Acta Mechanica, Vol. 211, pp. 293-307, 2010.

[21] M. Damircheli, M. Azadi, Temperature and thickness effects on thermal and mechanical stresses of rotating FG-disks, Journal of Mechanical Science and Technology, Vol. 25, No. 3, pp. 827-836, 2011.

[22] E. Bagherizadeh, Y. Kiani, M. R. Eslami, Mechanical buckling of functionally graded material cylindrical shells surrounded by Pasternak elastic foundation, Composite Structures, Vol. 93, pp. 3063–3071, 2011.

[23] E. Bagherizadeh, Y. Kiani, M. R. Eslami, Thermal Buckling of Functionally Graded Material Cylindrical Shells on Elastic Foundation, AIAA Journal, Vol. 50, No. 2, pp. 500-503, 2012.

[24] H. R. Ovesy, J. Fazilati, Parametric instability analysis of moderately thick FGM cylindrical panels using FSM, Computers and Structures, Vol. 108-109, pp. 135-143, 2012.

[25] H. R. Ovesy, S. A. M. Ghannadpour, M. Nassirnia, Post-buckling analysis of rectangular plates comprising Functionally Graded Strips in thermal environments, Computers and Structures, Vol. 147, pp. 209–215, 2015.

[26] M. H. Shojaeefard, A. Najibi, Nonlinear transient heat conduction analysis of hollow thick temperature-dependent 2D-FGM cylinders with finite length using numerical method, Journal of Mechanical Science and Technology, Vol. 28, No. 9, pp. 3825-3835, 2014.

[27] S. Wang, D. J. Dawe, Buckling of composite shell structures using the spline finite strip method, Composites: Part B, Vol. 30, pp. 351–364, 1999.

[28] J. N. Reddy, Mechanics of laminated composite plates and shells: theory and analysis, second ed., Boca Raton, FL: CRC Press, 2004.

[29] R. Javaheri, M. R. Eslami, Thermal buckling of functionally graded plates, AIAA Journal, Vol. 40, pp. 162–169, 2002.

[30] H. S. Shen, Functionally graded materials: nonlinear analysis of plates and shells, Boca Raton, FL: CRC Press, 2009.

[31] C. W. Lim, Y. F. Ma, S. Kitipornchai, C. M. Wang, R. K. K. Yuen, Buckling of Vertical Cylindrical Shells Under Combined End Pressure and Body Force, Journal of Engineering Mechanics, Vol. 129, pp. 876-884, 2003.

[32] S. B. Batdorf, A simplified method of elastic stability analysis for thin cylindrical shells; II-modified equilibrium equation: NACA Report 1342, 1947.

[33] H. R. Ovesy, J. Fazilati, Stability analysis of composite laminated plate and cylindrical shell structures using semi-analytical finite strip method, Composite Structures, Vol. 89, No. 3, pp. 467–474, 2009.

[34] S. P. Timoshenko, J. M. Gere, Theory of Elastic Stability, New York: McGraw-Hill, 1961.