Optimization Methods Applied to Stormwater Management Problems: A Review

Info: 16795 words (67 pages) Dissertation
Published: 9th Dec 2019

Share this: Facebook Twitter Reddit LinkedIn WhatsApp

Optimization Methods Applied to Stormwater Management Problems: A Review

A B S T R A C T

Stormwater management essentially aims at controlling the surface runoff in order to reduce water pollution, restore ecosystem integrity, and preserve the environment. Application of operations research on controlling stormwater management systems has been increased in recent years. This paper reviews and discusses several optimization problems studied on this field. Some of the developed commercial softwares are presented. Having evaluated the relevant state of the art, we have noticed that there is an upward trend towards sustainability of the stormwater management systems to deal with climate change. Despite this progress, there are still many areas to further develop stormwater management models, many of which relate to uncertainty sources identification, real time control, and the proper formulization of multi-objective problems.

Keywords: Stormwater Management, Optimization, Climate Change.

1- Introduction

Rapid population growth, industrialization, urban development and consequently the limitations of water resources are the issues that induce researchers to employ mathematical optimization methods as one of the most effective methods to design solutions to different water related issues such as watershed degradation, pollution, water scarcity, sewer overflows, floods and drought.

Stormwater management in urban areas, traditionally, seeks to ensure the safety of citizens and to protect the public and private property during wet weather. Following the awareness of the impacts of stormwater drainage on physical and chemical characteristics of the receiving water, other objectives were gradually added to these traditional objectives. Thus, stormwater management activities may include the optimal control of water quantity, water quality, erosion and sediment control, nonpoint source pollution control, channel protection and natural area protection (Minnesota Stormwater Steering Committee 2008; MDDEP and MAMROT, 2011). A stormwater management system can achieve its objectives by integrating all these types of controls. On the other hand, planning, design and control of stormwater management systems for sustainable development of water resources require the public participation; however, the main responsibility relies on the decision makers to evaluate the policies and their impacts on the economic, social and environmental changes. Hence, researchers try to use the best tools to make the best decisions. In all cases, mathematical models can be an effective way to optimize the system performance which is in direct relation to its components (Behera, Papa, and Adams 1999). Through a mathematical model, the physical processes could be described. Without violating the constraints.

Generally, the optimization problems can be categorized according to different criteria such as:

Based on the functions: Linear programming (LP), Quadratic programming (QP) and Non-linear programming (NLP)
Based on the decision variables: Continuous programming, Discrete programming including Integer programming (IP) and Binary programming (BP), and finally Mixed integer programming (MIP)
Based on the constraints: Constrained programming and Unconstrained programming
Based on convexity of functions: Convex optimization and Nonconvex optimization
Stochastic programming and Deterministic programming
Single objective optimization, bi-objective optimization or multi-objective optimization.

There are numerous other forms of optimization problems that are not included in the classification above, such as Bound constraints programming, Quadratic programming with quadratic constraints (QPQC), Non-linear least square programming, Non-smooth problems (NSP), and many others which are not as common as the aforementioned types.

In stormwater management area, depending on the target problem, most of the optimization approaches are found to be non-linear programming because of the continuously changing nature of the environmental phenomenon and the heterogeneity of the parameters in creation of a natural situation. For instance, in a reservoir system optimization problem, the complexity of the variables and processes like unregulated inflows, system demands, net evaporation and hydrologic parameters, leads to a complex non-linear programming problem (Labadie 2004). However, a non-linear programming problem can be solved using different algorithms depending on the degree of non-linearity of that optimization problem (Pleau, Marcoux, and Colas 1998); in many cases, the linear programming is preferable to simplify the mathematical resolution.

As the tensions and disputes over water-related issues are growing, many researchers are currently engaged in finding practical solutions for these issues. In this regard, both hydraulic and hydrological aspects of rainfall-runoff processes has been widely considered, including overland issues in either urban or natural settings, water transportation through rivers and drainage networks, and stormwater related infrastructures such as conventional pipes and Best Management Practices (BMPs). In all these aspects, the optimal design and operation has been of importance. This paper aims at providing a survey of literature in stormwater management issues that employ optimization methods to achieve an effective solution. To do so, a thorough categorization of these problems is presented to provide a better understanding of the current research issues and the criteria involved in the investigation of the problem. The outline of the paper is as follows. Section 2 presents the study purposes. In section 3, an explanation is provided for the scope of the review and the different perspectives that are investigated in the research. Section 3.1 studies the literature for two different systems, namely the combined sewers and stormwater management systems. In section 3.2, we divided the literature in two categories based on two control approaches: static control and real time control (RTC). As the uncertainty is an inseparable issue in environmental problems, section 3.3 presents the articles that pay attention to the uncertainties involved in their studied problem. In section 3.4, stormwater management optimization problems in the existing literature are investigated based on their objective function(s). The concluding remarks with some further study suggestions are provided in section 4.

2- Study goals

In this review article the goals are:

To collect an extensive list of scientific researches in the field of stormwater management with the application of optimization methods,
To facilitate the access to a variety of relevant references for researchers,
To identify the research gaps and indicate the major shortcomings of the literature, and finally,
To propose further studies for the advancement of the area of research.

3- Methodology

Studies on different optimization problems found in the field of stormwater management is investigated in this review. To gather the related literature, the SCOPUS database was searched by using the keywords optimization AND stormwater management OR urban drainage. Totally, 315 documents were found after limiting the search to the years 1986-2017. These documents cover a broad range of journals on Environmental science and engineering as some of them is shown in Table 1.

Table 1- Number of articles per journal

Journal	No. of Articles
Water Science and Technology	44
Journal of water resources planning	15
Water resources management	13
Environmental Modelling and Software	9
Urban Water Journal	7
Journal of environmental engineering	6
Water Switzerland	6
Proceedings of the World Environmental and Water Resources Congress 2010	6
Procedia Engineering	5

4- Modelling approaches

In this paper, we focus on reviewing the optimization problems related to stormwater management and identifying the prominent related research questions. To this aim, we discuss various strategies proposed in the literature and investigate the most significant objectives conducive to manage stormwater systems. Figure 1 expands the different perspectives of the survey to classify the previous published literature into several groups.

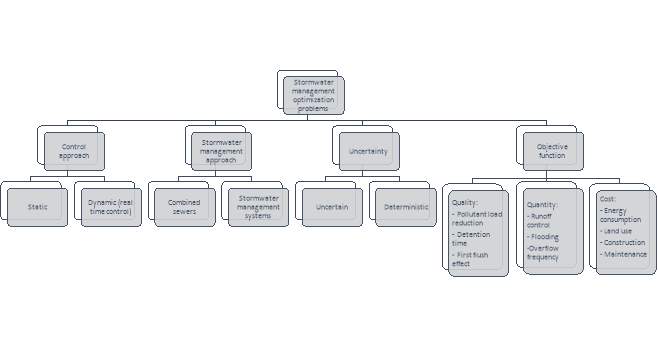
Figure 1- The optimization approach classification found in the literature

Table 1 provides a summary of stormwater management optimization studies and their models characteristics. In this table, the studied literature is presented in detail, based on the characteristics of the systems and models. This allows highlighting the combinations that have been less considered in the literature. From these studies will be investigated in this paper to propose areas where the models could be improved. To this aim, we have distinguished the stormwater management optimization models from four perspectives: i) the control approach which can be either dynamic or static, ii) the stormwater management approach including combined or separated sewer networks, iii) the uncertainty considerations, and iv) the objective function, that could be defined in terms of quality, quantity and/or cost.

Table 2-Summary of stormwater management optimization model characteristics found in the literature.

Reference

Control objectives

SWM[1] approach

Uncertainty

Control approach

Quality

Quantity

Cost

SWM

Uncertain

Deterministic

Static

Dynamic

Global

Local

Predictive

Reactive

Gaborit et al. (2012)

Travis et al. (2008)

Abraham et al. (1998)

Shamsudin et al. (2014)

Li and Matthew (1991)

Cembrano et al. (2004)

Fiorelli and Schutz (2009)

Vanrolleghem, Benedetti, and Meirlaen (2005)

Darsono and Labadie (2007)

Yeh and Labadie (1997)

Afshar (2010)

Zoltay et al. (2010)

Yazdi, Lee, and Kim (2014)

Vezzaro and Grum (2014)

Verdaguer et al. (2014)

Tung (1988)

Rauch and Harremoës (1999)

Martin Pleau et al. (2000)

Perez-Pedini, Limbrunner, and Vogel (2005)

Mobley, Culver, and Hall (2014)

Baek et al. (2015)

Reference

Control Objectives

SWM Approach

Uncertainty

Control Approach

Quality

Quantity

Cost

SWM

Stochastic

Deterministic

Static

Dynamic

Global

Local

Predictive

Reactive

Cano and Barkdoll (2016)

Chang, Rivera, and Wanielista (2011)

Che and Mays (2015)

Duchesne, Mailhot, and Villeneuve (2004)

Fu, Butler, and Khu (2008)

Jia et al. (2016)

Joseph-Duran et al. (2014)

Löwe et al. (2016)

Marinaki and Papageorgiou (2003)

Baek et al. (2015)

3-1- Based on stormwater management approach

The combined sewer system refers to a large network of pipes that carries municipal wastewater, including both sanitary and industrial water, combined with the surface runoff from stormwater. While the separate sewer network is designed to collect the wastewater and stormwater in two separated networks. This helps prevent the overflow to natural water courses of a combination of surface runoff with highly polluted residential and industrial wastewater. With the development of urban areas and growing population, separating stormwater from municipal wastewater became a matter and separate sewer systems were implemented in many recently constructed municipalities. However, in some parts of many developed cities (like New York City, Toronto, Philadelphia and London), the urban drainage system is still combined as changing the whole infrastructure would be too costly and time-intensive. Hence, there are still needs for solutions to manage the water resources for the combined sewer systems as well as separate stormwater systems. Optimization algorithms fall within the most useful approaches to manage the existing systems in the most efficient way.

3-1-1- Combined sewers

Optimization methods have been widely applied to combined sewer systems first, due to their capital-intensive nature and then, because they are known as the source of many urban river quality degradations, caused by combined sewer overflows (CSO) which occur when flows exceed the transport and/or the treatment capacity of the sewer system during wet weather. Using these methods helps researchers deal with many combined sewer related problems and also develop an optimal water resources management policy. Dajani and Gimmell (1971) were one of the firsts to formulate the wastewater sewer network as a mathematical nonlinear programming model, using a linear approximation for an optimal solution for the cost effectiveness problem through a computer software (Dajani and Gimmell, 1971). Hydraulic and hydrologic considerations have been also taken into account in mathematical models, where some of the system component characteristics such as conduit size, junction dimensions, buried depth of pipes and storage capacity were optimized to meet constraints and accomplish objectives (Dajani and Gammell, 1972, Froise and Burges, 1978). After a while, it has been found that a more efficient design of the urban drainage layout can lead to more significant savings than other alternatives. Li and Matthew (1991) developed a nonlinear programming model decomposed in two smaller models, one for the placement of pumping stations and the second for manipulating the flow rates in the pipes. Studies on location optimization of the different parts of the urban drainage system, like the online pumping stations (e.g. Froise and Burger 1978, Dajani and Gemmell 1972, Li and Matthew 1991), detention basins (e.g. Yeh and Labadie 1997), water quality sensors (e.g. Propato 2006) and treatment plants (e.g. Converse 1979), refers to the importance of the issue and efficiency of the optimization algorithms in achieving the solution.

A further and equally important consideration is the general control of the drainage network using numerical formulations, which has always been a matter of interest to researchers. Cembrano et al. (2004) investigated a combined sewer network which is optimally controlled to prevent overflows and reduce the risk of flooding through design of an optimization model. To do so, an objective function is defined as the sum of the quadratic flow deviations, CSOs and the volume stored in the reservoirs, prioritized with predefined coefficients and subject to several linear and non-linear equalities and inequalities to meet the flow equilibrium in the network.

Actually, despite the comprehensive literature on CSO control, because this issue is the most significant concern about the combined sewers, studies in this regard are still of increasing interests (Darsono and Labadie 2007; Regneri et al. 2010; Ocampo-Martinez et al. 2008; J.-P. Wang et al. 2007). Recently, Löwe et al. (2016) proposed a stochastic forecast-based optimization model for the real time control of an urban drainage system to minimize the volume of CSO. In general, real time control is one of the most conducive solutions to reduce the overflow volumes and frequencies in combined sewers (Duchesne et al. 2001), and has been widely discussed in the literature (Tobergte and Curtis 2013; Vezzaro et al. 2014; Gaborit et al. 2012; Borsanyi et al. 2008; Pleau et al. 2005). Studies on real time control of combined sewers will be presented in section 4-2-2.

3-1-2- Stormwater management systems

Stormwater management systems are designed for collection of surface runoff during wet periods. Stormwater runoff can sometimes be directed to a stormwater basin for further controls. Stormwater basins, as one of the most used stormwater Best Management Practices (BMP), have been developed and implemented to ensure the control of rainwater in terms of flow rates and/or runoff volumes, and improve water quality by sedimentation. Several studies have addressed the optimization of stormwater control measures with different criteria, and used a variety of techniques, for example: the optimal design of the location and size of detention basins for the control of flood in urban areas using a Genetic Algorithm (GA) (Yeh and Labadie 1997), runoff control in stormwater basin design, site by site, using dynamic programming (Behera, Papa, and Adams 1999), pollution load reduction by optimizing the detention time of a stormwater pond (Papa, Adams, and Guo 1999), design of a detention basin outlet to minimize alteration in the natural flow regime through simulation-optimization methodology (Mobley, Culver, and Hall 2014), and peak flow reduction at the outlet of a watershed using a distributed hydrologic model combined with a genetic algorithm to find the optimal number and location of infiltration-based BMPs (Perez-Pedini, Limbrunner, and Vogel 2005). Also, the combination of multiple criteria could be considered like in Shamsudin et al. (2014), where the maximization of runoff control performance of a detention pond and the minimization of the cost are studied using an analytical probabilistic model and the Particle swarm optimization (PSO).

However considering the operation of a single basin rather than that of a whole network can be misleading. For example, a concentration time balance in a single detention basin may cause a peak flow reduction in the related watershed but the final hydrograph in the receiving watercourse can be affected by flows from other upstream watersheds and cause critical conditions in the whole network. So, to obtain a global flow reduction plan, it is necessary to consider the whole network of pipes and detention ponds rather than studying them individually. Furthermore, only by having in mind stormwater basins as components of a network, the extreme rainfall events generating volumes exceeding each basin’s capacity, are controllable. Thus, global optimization of detention basins network from the perspective of flow, water quality and cost should definitely be beneficial.

3-2- Based on control approach

In a general definition, static optimization refers to “the process of minimizing or maximizing the costs/benefits of some action for one instant in time only”, while dynamic optimization describes the process of finding the optimal value of one or some objective functions over a period of time (Gregory 2002). In this study, by static control we mean a system which works without time consideration. In contrast, a dynamic control is taken as real time control (RTC) in which the control system performs on-line. In fact, a real time control action continuously receives data as input, processes them and finally updates the outputs, or set points, in small pre-specified time intervals which are mostly near real time. Stormwater management can benefit from various RTC modeling techniques and their applications are of increasing interests. The two next sections provide an overview of the static and dynamic control approaches of the stormwater management problems in the literature.

3-2-1- Static

Most of the literature on stormwater management modelling relies on static control approaches showing that there is still a big potential to apply dynamic considerations and think out of the box to design more realistic and flexible systems. For example, instead of taking the maximum outflow of a detention basin as a constant value in order to reduce the pollution of water from both small and heavy rainfall events (as in Middleton and Barrett 2008), a flexible outflow rate could be more efficient to satisfy the control of water quality.

Although there is no doubt that a dynamic system should perform more efficient in most of the cases, sometimes, a statically operating procedure can avoid any extra expenditures and any additional energy consumptions or even increase the life expectancy of the involved equipment (Pleau et al. 2013). Moreover, in a static optimization strategy, the execution time of the program is not important since the optimization is realized only once, and off-line. This allows evaluating the possible solutions more productively increasing the probability of achieving a more optimal strategy (Ray 2009). However, in many environmental issues, the variation in time of the control variables and processes is critically important such that real time consideration is desired.

3-2-2- Dynamic

The control of a system is said to be dynamic when a physical variable of the system is required to follow or track some pre-specified time function. In this study, more specifically, the focus is on RTC, i.e. the process where variables are measured in the system continuously and used to operate actuators (Garcia 2014) at the same rate of providing input data to the system, which mainly happens in very short time-steps. Recent advances in information technology and high-speed processors facilitate the implementation of RTC systems in various applications. Due to the continuously required control actions and the dynamic nature of stormwater management systems, the application of RTC on these systems, also, can give proper results. RTC applications have been studied in different stormwater management systems to minimize CSOs (Tobergte and Curtis 2013; Vezzaro et al. 2014; Pleau et al. 2001; Vezzaro and Grum 2014; Duchesne, Mailhot, and Villeneuve 2004; Marinaki and Papageorgiou 2003), to minimize the pollution load (Gaborit et al. 2012; Lacour and Schütze 2011; Hoppe et al. 2011), to minimize the cost (Pleau et al. 2005), to prevent flooding, to maximize the waste water treatment plant (WWTP) capacity and also to maximize the utilization of regulating devices like mobile gates, inflatable dams, variable speed pumps and variable crest weirs (Pleau et al. 2005).

Generally, RTC systems can be distinguished in regard to their control level or data type. In terms of levels of control, two levels have been studied, global and local, such that the global control level is responsible to provide the required set-points for the local controllers using the information gathered from all the system, while at local level, all the set points are determined locally for each part of the system (Vanrolleghem, Benedetti, and Meirlaen 2005; Pleau et al. 2001). On the other hand, RTC systems can be performed reactively or predictively. A reactive RTC system takes the control decisions based on the past and actual system data whereas a predictive system also uses predicted data as inputs to define the control actions (Vanrolleghem, Benedetti, and Meirlaen 2005; Duchesne, Mailhot, and Villeneuve 2004). In this regard, a global predictive RTC system was designed by Pleau et al. (2001) to reduce the frequency of CSOs using a non-linear programming package to produce flow set-points and optimize a multi criteria model constrained by the hydraulic and hydrologic linear equalities and inequalities for the Quebec City’s sewer network. The application of global predictive RTC approach in this study resulted in a 60% reduction in overflow volumes compared to a static approach.

Optimization algorithms have been already applied to RTC of stormwater management problems in the literature, however, it is still an ongoing field. Marinaki and Papageorgiou (2003) developed a linear multi-variable feedback regulator to prevent overflows in a sewer network through a linear-quadratic design procedure. In their study, by maximizing the utilization of the reservoir’s available storage space and draining it as soon as possible to provide the space for future rainfall event, the optimization problem aims at minimizing the combined network overflows.

Other optimization algorithms applied to solve stormwater management problems include the use of meta-heuristic programming models, like the bio-inspired mathematical algorithms (Afshar 2010) that, due to their independency of the functions derivatives, can be used to solve many complex, non-linear and multi-objective optimization problems. For example, finding the optimal flows between the detention basin and WWTP using GA to minimize the global cost function in RTC of an urban drainage system in Vezzaro and Grum (2014) or employing a nonlinear model predictive control (MPC) combined with a genetic algorithm to minimize transit pollution from an urban wastewater system (Rauch and Harremoës 1999). A detailed description of several techniques and strategies, including optimization-based algorithms applied to urban drainage systems, can be found in García et al. (2015).

3-3- Based on uncertainty

The infeasible solutions or even those feasible solutions that mislead decision makers to take improper actions, are the results of having uncertainties in system parameters and variables. However, the costly and time consuming nature of uncertainty analysis somehow hinder researchers to consider them in their investigations, but the tendency to design the models as close as possible to reality leads to significant advances in developing robust based models. In the stormwater management field, like every other fields, there are uncertainties in model parameters, input data, calibration data or in the model structure (Dotto et al. 2012). The next two sections will expand on stormwater management deterministic and stochastic optimization models found in the literature.

3-3-1- Deterministic models

Several optimization models have been reported in the literature in which all the model components are considered to be deterministic (e.g. Abraham et al. 1998; Afshar 2007; Afshar 2010; Baek et al. 2015; Baek et al. 2015; Cembrano et al. 2004; Erbe et al. 2002; Fiorelli and Schutz 2009; Gaborit et al. 2012; Travis et al. 2008; Tung 1988). These studies mainly aim at introducing a new approach (Joseph-Duran et al. 2014), developing a new mathematical model (Montaseri, Afshar, and Bozorg-Haddad 2015) or proposing a corrigendum to an already existing solution (Afshar 2010). For example, Baek et al. (2015) investigated a new meta-heuristic particle swarm optimization approach for a multiple storage sewer network to control the CSOs. To do so, a mathematical formulation of the simplified system is modeled to finally optimize the location and storage size of multiple storage tanks. In this study, the main focus is on developing an already existing method to solve an environmental problem in which, however, there are many uncertainties involved, the reasonable strategy is to consider all the model components deterministic to avoid any complexity in the model and provide a better description of the newly developed methodology. Generally, in presence of uncertainty, although in most of the cases stochastic models are more realistic, deterministic models are more convenient to use when the sources of uncertainty are negligible or when considering them leads to high complexity of model, and consequently causes the digression from the main research subject.

3-3-2- Uncertainty-based models

Unlike deterministic models where all the outputs are the exact result of the cause and effect relationships between all the system’s components, uncertainty-based models often have varying results for the same set of initial inputs, due to the random nature of their components or processes (Obropta and Kardos 2007). Inaccuracy of measurement devices in providing the exact value of model variables such as flow rates, rainfall intensity, water pollution and water level, uncertainties regarding maximum flow rates, estimation of CSO discharges based on rainfall time series (Regneri 2014), uncertainties caused by modeling mismatches and simplifications (Pleau et al. 2002), and prediction uncertainties (Löwe et al. 2014), like the rainfall depth and duration in Yazdi, Lee, and Kim (2014) or runoff predictions in Vezzaro and Grum (2014), are some of the sources of uncertainties brought in the urban stormwater modelling literature. For example, in build-up and wash-off runoff quality model, uncertainty would cause inevitable unreliability. In this kind of model, “build-up” of water contaminants on impervious surfaces during dry periods results in “wash-off” of the pollutants in wet periods. As these processes in reality are more complicated than those modeled (Petrucci 2017), it comes often with uncertainty (Obropta and Kardos 2007). Clearly, the degree of uncertainty is a function of model characteristics. Regneri (2014) reports for instance, as the length of the forecast horizon increases the uncertainty of predicted data gets worse. Shrestha (2009) suggested that for achieving a reliable and more realistic modeling, it is necessary to: 1) recognize the sources of uncertainty; 2) express the detected uncertainty numerically; 3) assess its propagation through the model; and 4) propose solutions to mitigate their consequences. To this aim, several approaches have been employed to counteract the uncertainty effects on the stormwater management operations. Vezzaro and Grum (2014) presented a Dynamic Overflow Risk Assessment (DORA) strategy as a global control approach to estimate the uncertainty of urban runoff forecasts in a Model Predictive Control (MPC) of urban drainage network, and subsequently minimize CSO costs within the entire catchment. Also, the Generalized Likelihood Uncertainty Estimation (GLUE), which is a Monte Carlo based approach introduced by Beven and Binley (1992), has been widely used in the quantity and quality modelling of urban stormwater (Dotto et al. 2012), as in Jia and Culver (2006) where a robust optimization model is developed to incorporate the uncertainty of water quality predictions and to minimize pollutant load reduction using the GLUE approach.

Besides, as in many cases, a probability distribution function is imaginable for the uncertain hydrologic or hydraulic variables, the stochastic methods have received lots of attention in stormwater management studies. The probabilistic Huff method (Huff 1990) was applied to determine the probability distribution of two uncertain rainfall variables, depth and duration, to utilize in stochastic multi-criteria optimization model of urban drainage system rehabilitation (Yazdi, Lee, and Kim 2014). In another work, the previously-introduced method, DORA, has been combined with a stochastic grey-box model to deal with the probabilistic nature of runoff forecasting to RTC of urban drainage system (Löwe et al. 2014). Recently, Yu et al. (2017) proposed a stochastic optimization model for urban drainage design in order to achieve a more robust optimal solution to the effects of urban hydrological model parameter uncertainty. The trade-off between the total investment on drainage network rehabilitation and flood control goals have been conducted to solve the problem using heuristic algorithms while employing techniques of urban hydrological simulation and climate-change model downscaling. The results showed a higher level of system reliability in stochastic model, compared to deterministic one.

Generally, the negative impacts of uncertainties on the productivity of the strategies that decision makers employ to cope with the urban stormwater management issues, have given rise to many uncertainty techniques for the development of more reliable optimization models. Although these techniques have evolved gradually from very simple to more complex forms, detection of new sources of uncertainty has influenced the reliability of the developed models. Therefore, not only, the invention of new heuristic would be beneficial, but also the decision making based on stochastic programming can markedly contribute to a more realistic modeling of dynamic processes.

3-4- Based on objective function

Many different criteria can be minimized, or maximized, when studying a stormwater management optimization problem, generally called cost function or objective function. Stormwater management objectives can be classified under three main headings – ensuring the quality of water, quantity considerations and cost minimization. In the following sections, the use of these objectives in the literature will be explicitly explained.

3-4-1- Water quality

One of the main consequences of urbanization is the degradation of surface water quality which can affect directly public health and ecosystems. Therefore, stormwater quality considerations have become one of the critical challenges that stormwater management was engaged with (Obropta and Kardos 2007). Besides, the growing impact of urban stormwater on the vulnerability of water resources raised the need for more accurate modeling of stormwater pollution (Beck 2005). Throughout the years, researchers have been studying different aspects of water pollution in their mathematical models and trying to propose solutions to overcome the factors that negatively affect the quality of water. Pollutant load reduction, detention time optimization, first flush effect minimization, storage facility de-watering time optimization are some of the control objectives studied to achieve the desired water quality in terms of optimization applications. For instance, a nonlinear model predictive control has been employed in Rauch and Harremoës (1999) to provide a flexible formulation for real-time control of urban wastewater system to minimize transient pollution. Papa, Adams, and Guo (1999) proposed two parallel formulations in order to maximize the long-term performance of a dry detention pond to more effectively remove total suspended solids (TSS) by selecting the optimal stormwater management pond detention times. Although detention time maximization is one of the major factors in stormwater basin design to enhance its TSS removal (Shammaa et al. 2002), sometimes it leads to more overflows due to heavy rainfall. By designing an adjustable pond’s gate opening, hence, a flexible structure can be provided in order to maximize the detention time to improve the TSS removal while protecting the receiving water bodies from hydraulic shocks and minimizing the probability of overflow (Gaborit et al. 2012). The outlet control in stormwater ponds could be considered as a key factor in optimization of stormwater management systems to protect water quality while avoiding any overflow in the receiving body, such that in Mobley and Culver (2014), Mobley, Culver, and Hall (2014), Gaborit et al. (2012), and Middleton and Barrett (2008). A few other criteria have been studied in the literature to preserve water quality such as i) minimization of the first flush effect (Baek et al. 2015; Verdaguer et al. 2014; Abrishamchi, Massoudieh, and Kayhanian 2010), which implies a greater wash-out pollutants in the water remains from the first period of a storm (Verdaguer et al. 2014), ii) sediment-trapping BMP placement optimization, in which the results from the linear and dynamic programming are compared with a new method using a GA optimization and a nonlinear distributed watershed model in Limbrunner and Vogel (2013), and iii) the optimization of stormwater filtration to accommodate Total Maximum Daily Loads (TMDL) as in Hipp, Lejano, and Smith (2006).

3-4-2- Quantity

Stormwater management puts many efforts on the control of water quantity so that the specialties in this field have been trying to simulate realistically the urban stormwater behavior, to define the optimal control performance of an effective stormwater management system and to prevent the undesired consequences of urban runoff in different ways. Failure in controlling the quantity of stormwater, especially in urban areas, may result in irreparable damages to infrastructure, but also to the quality of water resources, like when the CSOs in an industrial area discharge over-polluted water to the nearby streams, rivers and other water bodies. Efforts to minimize CSOs have prompted researchers to consider the CSO control as the main objective of their optimization problem, either in terms of CSO frequency mitigation (Saber-Freedman 2016; Pleau et al. 2001) or overflow volume reduction (Vezzaro and Grum 2014; Joseph-Duran et al. 2014). In this regard, a number of optimization-based techniques have been developed to minimize undesired sewage discharges. Baek et al. (2015) presented a meta-heuristic particle swarm optimization-based design methodology of complex sewer networks to investigate the optimally distributed locations, sizes and numbers of multiple reservoirs for efficient CSO reduction.

There are some traditional flood control ponds, whose function is primarily to attenuate peak flow rates (Papa, Adams, and Guo 1999). Although these ponds are being replaced by more equipped stormwater basins, the minimization of flooding is still a subject of interest. Reservoir operation is one of the solutions that is studied widely in the literature to control flooding through various optimization methods: linear programming (Needham et al. 2000; Watkins, Jones, and Ford 1999), goal programming (Choudhury 2010), non-linear programming (Unver and Mays 1990), dynamic modeling (Che and Mays 2015) and fuzzy optimization methods ( Jia et al. 2016; Zamani Sabzi et al. 2016).

Other criteria that have been addressed in the stormwater management literature based on the quantity of stormwater include runoff quantity minimization (Gaborit et al. 2012; Papa, Adams, and Guo 1999; Cembrano et al. 2004), overflow frequency and volume minimization (Tung 1988; Cembrano et al. 2004) and flow equalization.

3-4-3- Cost

Alongside with the above-mentioned objectives, the costs involved in stormwater management, especially in urban areas, have always been an issue of concern. The existing literature provides an extensive list of cost objective functions to be considered in stormwater management problems. Costs of land use, construction and maintenance of stormwater management systems are the most traditional components of objective functions found in the literature (Tung 1988; Abraham et al. 1998; Travis et al. 2008; Vezzaro et al. 2014). These objectives can be considered as the main criteria in different control problems. For example, the storage-release systems, that aim at controlling stormwater quantity (runoff) and its quality through defining long-term performance measures, such as the overall fraction of runoff controlled and the fraction of pollutant removal from the storage facilities (Chen and Adams 2006), can be described as an optimization model. The aim of this model can be minimization of construction cost of stormwater management ponds while ensuring both the water quality and runoff quantity, as studied in Behera, Papa, and Adams (1999). In addition, the total cost minimization has also been considered as the objective function in Sebti, Bennis, and Fuamba (2013) where the cost-effectiveness of the urban drainage system rehabilitation is assessed by a proposed algorithm considering both structural and hydraulic performances.

Also, in several studies, cost minimization comes along with other objectives and forms a multi-criteria optimization problem. Tung (1988), as one of the firsts, proposed a framework to establish the trade-off between the risk of overflow and the cost of storage and treatment capacities through designing a multi-objective detention basin optimization model. Recently, Cano and Barkdoll (2016) introduced the multi-objective, socio-economic, boundary-emanating, nearest distance (MOSEBEND) algorithm that allows the optimal selection and placement of a set of BMPs for various sub-watersheds. The cost objective function used here is assumed to be a cost-benefit ratio in which the cost is the opportunity costs of using the land for the BMP instead of its original use, while the benefit is defined as runoff reduction or, alternatively, the level of pollution reduction. Somewhere else in the literature, the minimization of implementation cost objective comes along with the minimization of peak-flow, runoff volume and HFR stormwater metric alteration, reprehensively in three optimization model in order to achieve near optimal locations of green roofs and permeable pavements as two stormwater LIDs (Giacomoni and Joseph 2017).

While the most significant costs in a stormwater management system are related to the initial investments and the maintenance, some other expenditures are involved that cannot be easily denied. For instance, following the general increasing awareness of the limited resources of energy and considering this issue in the political agenda, the energy saving strategies have also been brought up in the recent studies (Chang, Rivera, and Wanielista 2011; Zoltay et al. 2010; Wang, Saavedra Valeriano, and Sun 2013). In this regard, Chang, Rivera, and Wanielista (2011) proposed a grey stochastic linear programming model to achieve a degree of energy savings and stormwater conservations considering the optimal design of green roofs as one of the BMPs. In this study, it is proved that the benefits of such systems due to the long-term saving of energy is considerable and can offset the initial capital and ongoing maintenance costs of the system. In general, the consumption of energy is one of the today’s global concerns and almost all the research areas are somehow involved in finding energy saving strategies, and stormwater management is no exception.

3-5- Optimization using commercial software packages

Throughout the years, many commercial software packages have been developed to simulate single events and continuous rainfall-runoff quantity and quality modelling in sewer networks in urban areas. One of the most widely utilized models in North America is the Stormwater Management Model known as SWMM, developed by the United States Environmental Protection Agency (EPA) (Rossman and Huber 2016) and used as the base model of some commercial software packages. However, even if these packages have been widely employed to evaluate the optimization approaches proposed in the literature (e.g. Yazdi, Lee, and Kim 2014; Darsono and Labadie 2007), they are not capable of doing optimization themselves. We have identified a few commercial tools, addressed in the literature, with the aim of optimizing some stormwater management problems. In the following a brief description of four of these tools is brought.

SUSTAIN

The System for Storm-water treatment and Analysis Integration (SUSTAIN) is a decision support system developed in 2003 by the EPA collaborating with Tetra Tech, to investigate different stormwater quantity and quality management strategies and also to evaluate the implementation of different BMP scenarios at multiple spatial scales, ranging from local to broad watershed applications, based on either a single storm event or a long-term continuous simulation. SUSTAIN operates based on the ArcGIS platform and encompasses six modules (Lee et al. 2012): a BMP sitting tool with which SUSTAIN is able to optimize the location, type and cost of different BMP/LIDs (Low Impact Development) like in Mao, Jia, and Yu (2017), a watershed runoff and routing module, a BMP simulation module, a BMP cost analysis module, an optimization module, and a post-processor. The optimization core of SUSTAIN is the optimization module which uses two metaheuristic optimization algorithms, Scatter search and Non-dominated Sorting Genetic Algorithm-II (NSGA-II), to provide a solution for non-linear, multi-objective and complex optimization problems (Lee et al. 2012).

Csoft

Csoft is a global predictive RTC simulation software designed by BPR-CSO commercial software development group in order to first, simulate the hydraulic behavior of the sewer network and then, optimize the performance of the sewer system (Grondin et al. 2002). This software contains a simulation-optimization module which performs based on the mathematical formulations introduced in the user’s manual (Pleau and Pelletier 2000). The objective function of the optimization part could be defined to meet different system goals such as energy consumption control, dewatering time minimization, flooding risk reduction, CSO control and flow equalization at the WWTP and the choice of the objective function depends on the circumstances under which the system performs, like wet weather, dry weather, critical events and system breakdown (Tetra Tech 2016).

StormWISE

The Storm Water Investment Strategy Evaluator (StormWISE) is a tool to optimize the total investment on the implementation of new stormwater management systems, BMPs and LIDs, for strategic water quality preservation. The tool performs based on a multi-criteria constrained optimization model which is formulated with nonlinear benefit functions represented by the piecewise linear segments for an optimal sizing and placement of BMP/LID projects at drainage zones (McGarity 2012).

Liu et al. (2016) decision support tool

Recently, a decision support tool was developed by Liu et al. (2016) for the optimal selection and placement of BMP/LID practices and to provide a trade-off between the cost minimization and the runoff and pollutant load reduction objectives. This optimization framework performs based on the collaboration of the L-THIA-LID 2.1 hydrologic/water quality simulation model, the optimization algorithms of AMALGAM and the multilevel spatial optimization (MLSOPT) to reduce the complexity of the optimization problem.

5- Concluding remarks and further studies

Our review encompasses various optimization problems studied in the field of stormwater management. It provides a review of over eighty papers from the major referenced journals within the field. According to the data from the collected literature, approximately 70% of the articles published in the last 10 years, in spite of some fluctuations, occurred in recent years; and the overall trend of publication numbers in this area has been upward (Figure 2).

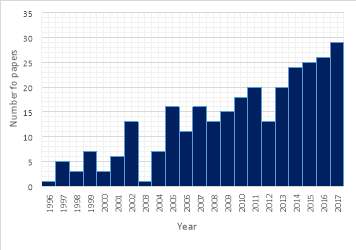
Figure 2-The accumulated number of papers published within the studied field from 1996 to 2017

But the efforts should be continued to complete the execution of the already proposed strategies, and to explore some unexpected challenges involved in established systems. For instance, in different parts of the world, there are many cities in which the urban drainage systems are controlled locally by simple RTC systems (Beeneken et al. 2013), while there exist only a few cities equipped with advanced global RTC systems as Quebec (Pleau et al. 2005), Vienna (Fuchs and Beeneken 2005) and Dresden (Fuchs, Günther, and Lindenberg 2004). There is still a huge potential for sustainable management of urban stormwater and its adaptability to climate change, and optimization methods are strong tools to achieve this aim. Therefore, utilizing the full potential of the optimization tools and applying new heuristic algorithms and programming methods to provide effective strategies, are desirable. Specifically, because it has been widely demonstrated that despite the growing invested capital, the actual technical systems perform ineffectively in critical situations due to the lack of “a strong scientific or theoretical foundation” (Labadie 2004) . Therefore, we defined some research gaps in the stormwater management studies based on the provided review, as follows: 1) perusal of the effects of the sources of uncertainty in the stormwater management systems which are controlled dynamically to deal with the unpredictable hydrologic processes; 2) a proper trade-off between all three quality, quantity and cost objective functions simultaneously in combined sewer investigations; 3) global predictive real time control of stormwater management systems; and finally 4) designing reliable apparatuses that would perform based on accurate algorithms to optimize the performance of systems in order to respond to the future conditions, in terms of the rapid changing climate and land use.

In sum, the current global concerns regarding climate change, the rapid growth of the urban areas and the random nature of rain events require the systems to be managed dynamically to deal with complexity and instability of the environmental conditions, and this aim is not attainable except by exploiting the full potential of the existing tools; In this regard, optimization methods have been proven as strong tools to deal with the stormwater management issues.

6- References

Abraham, Dulcy M., Reini Wirahadikusumah, T. J. Short, and Shahpor Shahbahrami. 1998. “Optimization Modeling for Sewer Network Management.” Journal of Construction Engineering and Management 124 (5): 402–10. doi:10.1061/(ASCE)0733-9364(1998)124:5(402).

Abrishamchi, A, A Massoudieh, and M Kayhanian. 2010. “Probabilistic Modeling of Detention Basins for Highway Stormwater Runoff Pollutant Removal Efficiency.” Urban Water Journal 7 (6): 357–66. doi:10.1080/1573062x.2010.528434.

Afshar, M. H. 2007. “Partially Constrained Ant Colony Optimization Algorithm for the Solution of Constrained Optimization Problems: Application to Storm Water Network Design.” Advances in Water Resources 30 (4): 954–65. doi:10.1016/j.advwatres.2006.08.004.

———. 2010. “A Parameter Free Continuous Ant Colony Optimization Algorithm for the Optimal Design of Storm Sewer Networks: Constrained and Unconstrained Approach.” Advances in Engineering Software 41 (2). Elsevier Ltd: 188–95. doi:10.1016/j.advengsoft.2009.09.009.

Baek, Hyunwook, Jaena Ryu, Jeill Oh, and Tae Hyoung Kim. 2015. “Optimal Design of Multi-Storage Network for Combined Sewer Overflow Management Using a Diversity-Guided, Cyclic-Networking Particle Swarm Optimizer – A Case Study in the Gunja Subcatchment Area, Korea.” Expert Systems with Applications 42 (20). Elsevier Ltd: 6966–75. doi:10.1016/j.eswa.2015.04.049.

Baek, Sang Soo, Dong Ho Choi, Jae Woon Jung, Hyung Jin Lee, Hyuk Lee, Kwang Sik Yoon, and Kyung Hwa Cho. 2015. “Optimizing Low Impact Development (LID) for Stormwater Runoff Treatment in Urban Area, Korea: Experimental and Modeling Approach.” Water Research 86. Elsevier Ltd: 122–31. doi:10.1016/j.watres.2015.08.038.

Beeneken, T, V Erbe, A Messmer, C Reder, R Rohlfing, M Scheer, M Schuetze, et al. 2013. “Real Time Control (RTC) of Urban Drainage Systems – A Discussion of the Additional Efforts Compared to Conventionally Operated Systems.” Urban Water Journal 10 (5): 293–99. doi:10.1080/1573062x.2013.790980.

Behera, Pradeep Kumar, Fabian Papa, and Barry J Adams. 1999. “Optimization of Regional Storm-Water Management Systems.” Journal of Water Resources Planning and Management 125 (2): 107–14. doi:10.1061/(ASCE)0733-9496(1999)125:2(107).

Beven, Keith, and Andrew Binley. 1992. “The Future of Distributed Models: Model Calibration and Uncertainity Prediction.” Hydrol. Process. 6 (May 1991): 279–98. doi:10.1002/hyp.3360060305.

Borsanyi, P., L. Benedetti, G. Dirckx, W. De Keyser, D. Muschalla, A. Solvi, V. Vandenberghe, M. Weyand, and P. Vanrolleghem. 2008. “Modelling Real-Time Control Operations on Virtual Sewer Systems.” Journal of Environmental Engineering and Science 7 (January): 395–410. doi:10.1139/S08-004.

Cano, Olga M., and Brian D. Barkdoll. 2016. “Multiobjective, Socioeconomic, Boundary-Emanating, Nearest Distance Algorithm for Stormwater Low-Impact BMP Selection and Placement.” Journal of Water Resources Planning and Management, 5016013. doi:10.1061/(ASCE)WR.1943-5452.0000726.

Cembrano, G., J. Quevedo, M. Salamero, V. Puig, J. Figueras, and J. Marti. 2004. “Optimal Control of Urban Drainage Systems. A Case Study.” Control Engineering Practice 12 (1): 1–9. doi:10.1016/S0967-0661(02)00280-0.

Chang, Ni-Bin, Brian John Rivera, and Martin P Wanielista. 2011. “Optimal Design for Water Conservation and Energy Savings Using Green Roofs in a Green Building under Mixed Uncertainties.” Journal of Cleaner Production In Press, (11). Elsevier Ltd: 1180–88. doi:10.1016/j.jclepro.2011.02.008.

Che, Daniel, and Larry W. Mays. 2015. “Development of an Optimization/Simulation Model for Real-Time Flood-Control Operation of River-Reservoirs Systems.” Water Resources Management 29 (11): 3987–4005. doi:10.1007/s11269-015-1041-8.

Choudhury, Parthasarathi. 2010. “Reservoir Flood Control Operation Model Incorporating Multiple Uncontrolled Water Flows.” Lakes and Reservoirs: Research and Management 15 (2): 153–63. doi:10.1111/j.1440-1770.2010.00431.x.

Darsono, Suseno, and John W. Labadie. 2007. “Neural-Optimal Control Algorithm for Real-Time Regulation of in-Line Storage in Combined Sewer Systems.” Environmental Modelling and Software 22 (9): 1349–61. doi:10.1016/j.envsoft.2006.09.005.

Dotto, Cintia B S, Giorgio Mannina, Manfred Kleidorfer, Luca Vezzaro, Malte Henrichs, David T. McCarthy, Gabriele Freni, Wolfgang Rauch, and Ana Deletic. 2012. “Comparison of Different Uncertainty Techniques in Urban Stormwater Quantity and Quality Modelling.” Water Research 46 (8). Elsevier Ltd: 2545–58. doi:10.1016/j.watres.2012.02.009.

Duchesne, Sophie, Alain Mailhot, Emeric Dequidt, and Jean Pierre Villeneuve. 2001. “Mathematical Modeling of Sewers under Surcharge for Real Time Control of Combined Sewer Overflows.” Urban Water 3 (4): 241–52. doi:10.1016/S1462-0758(01)00037-1.

Duchesne, Sophie, Alain Mailhot, and Jean-Pierre Villeneuve. 2004. “Global Predictive Real-Time Control of Sewers Allowing Surcharged Flows.” Journal of Environmental Engineering 130 (5): 526–34. doi:10.1061/(ASCE)0733-9372(2004)130:5(526).

Erbe, V, T Frehmann, W F Geiger, P Krebs, J Londong, and K Seggelke. 2002. “Integrated Modelling as an Analysing and Optimisation Tool for Urban Watershed Management.” Water Science and Technology 46 (6–7): 141–50.

Fiorelli, D., and G. Schutz. 2009. “Real-Time Control of a Sewer Network Using a Multi-Goal Objective Function.” 2009 17th Mediterranean Conference on Control and Automation, 676–81. doi:10.1109/MED.2009.5164621.

Fu, Guangtao, David Butler, and Soon-Thiam Khu. 2008. “Multiple Objective Optimal Control of Integrated Urban Wastewater Systems.” Environmental Modelling & Software 23 (2): 225–34. doi:10.1016/j.envsoft.2007.06.003.

Fuchs, L, and T Beeneken. 2005. “Development and Implementation of a Real-Time Control Strategy for the Sewer System of the City of Vienna.” Water Science and Technology 52 (5): 187–94.

Fuchs, L, H Günther, and M Lindenberg. 2004. “Minimizing the Water Pollution Load by Means of Real-Time Control – The Dresden Example.” In Proceedings of the 6th International Conference on Urban Drainage Modelling.

Gaborit, E., D. Muschalla, B. Vallet, P. A. Vanrolleghem, and F. Anctil. 2012. “Improving the Performance of Stormwater Detention Basins by Real-Time Control Using Rainfall Forecasts.” Urban Water Journal 10 (4): 1–17. doi:10.1080/1573062X.2012.726229.

Garcia, L. 2014. “On the Modeling and Real Time Control of Urban Drainage System : A Survey.” In 11th Conference on Hydroinformatics, New York City, USA.

García, L., J. Barreiro-Gomez, E. Escobar, D. Téllez, N. Quijano, and C. Ocampo-Martinez. 2015. “Modeling and Real-Time Control of Urban Drainage Systems: A Review.” Advances in Water Resources 85: 120–32. doi:10.1016/j.advwatres.2015.08.007.

Giacomoni, M H, and John Joseph. 2017. “Multi-Objective Evolutionary Optimization and Monte Carlo Simulation for Placement of Low Impact Development in the Catchment Scale” 2 (9): 1–15. doi:10.1061/(ASCE)WR.1943-5452.0000812.

Gregory, Robert W. 2002. “Biomechanics and Control of Torque Production During Prehension.” Thesis.

Grondin, François, Marco Grondin, Hubert Colas, Martin Pleau, Pierre Lavallée, Boulevard Hamel Ouest, and Quebec City. 2002. “Csoft – A New Software for the Design and Real Time Operation of Sewer Networks François Grondin, Marco Grondin, Hubert Colas, Martin Pleau and Pierre Lavallée BPR-CSO, 4655, Boulevard Hamel Ouest, Quebec City, Quebec, G1P 2J7, Canada.” Global Solutions for Urban Drainage.

Hipp, J Aaron, Raul Lejano, and C Scott Smith. 2006. “Optimization of Stormwater Filtration at the Urban / Watershed Interface.” Environ. Sci. Technol. 40 (15): 4794–4801.

Hoppe, H., S. Messmann, A. Giga, and H. Gruening. 2011. “A Real-Time Control Strategy for Separation of Highly Polluted Storm Water Based on UV-Vis Online Measurements – From Theory to Operation.” Water Science and Technology 63 (10): 2287–93. doi:10.2166/wst.2011.164.

Huff, Floyd A. 1990. Time Distribution of Heavy Rainstorm in Illinios.

Jia, Benyou, Slobodan P. Simonovic, Pingan Zhong, and Zhongbo Yu. 2016. “A Multi-Objective Best Compromise Decision Model for Real-Time Flood Mitigation Operations of Multi-Reservoir System.” Water Resources Management 30 (10). Water Resources Management: 3363–87. doi:10.1007/s11269-016-1356-0.

Jia, Yanbing, and Teresa B. Culver. 2006. “Robust Optimization for Total Maximum Daily Load Allocations.” Water Resources Research 42 (2): 1–10. doi:10.1029/2005WR004079.

Joseph-Duran, Bernat, Michael N. Jung, Carlos Ocampo-Martinez, Sebastian Sager, and Gabriela Cembrano. 2014. “Minimization of Sewage Network Overflow.” Water Resources Management 28 (1): 41–63. doi:10.1007/s11269-013-0468-z.

Labadie, John W. 2004. “Optimal Operation of Multireservoir Systems: State-of-the-Art Review.” Journal of Water Resources Planning and Management 130 (2): 93–111. doi:10.1061/(ASCE)0733-9496(2004)130:2(93).

Lacour, C., and M. Schütze. 2011. “Real-Time Control of Sewer Systems Using Turbidity Measurements.” Water Science and Technology 63 (11): 2628–32. doi:10.2166/wst.2011.159.

Li, By Guiyi, and Robert G S Matthew. 1991. “New Approach for Optimization of Urban Drainage Systems” 116 (5): 927–44.

Limbrunner, JF, and RM Vogel. 2013. “Classic Optimization Techniques Applied to Stormwater and Nonpoint Source Pollution Management at the Watershed Scale.” … and Management 139 (October): 486–91. doi:10.1061/(ASCE)WR.1943-5452.0000361.

Liu, Yaoze, Raj Cibin, Vincent F. Bralts, Indrajeet Chaubey, Laura C. Bowling, and Bernard A. Engel. 2016. “Optimal Selection and Placement of BMPs and LID Practices with a Rainfall-Runoff Model.” Environmental Modelling and Software 80. Elsevier Ltd: 281–96. doi:10.1016/j.envsoft.2016.03.005.

Löwe, Roland, Søren Thorndahl, Peter Steen Mikkelsen, Michael R. Rasmussen, and Henrik Madsen. 2014. “Probabilistic Online Runoff Forecasting for Urban Catchments Using Inputs from Rain Gauges as Well as Statically and Dynamically Adjusted Weather Radar.” Journal of Hydrology 512. Elsevier B.V.: 397–407. doi:10.1016/j.jhydrol.2014.03.027.

Löwe, Roland, Luca Vezzaro, Peter Steen Mikkelsen, Morten Grum, and Henrik Madsen. 2016. “Probabilistic Runoff Volume Forecasting in Risk-Based Optimization for RTC of Urban Drainage Systems.” Environmental Modelling and Software 80: 143–58. doi:10.1016/j.envsoft.2016.02.027.

Mao, Xuhui, Haifeng Jia, and Shaw L Yu. 2017. “Assessing the Ecological Benefits of Aggregate LID-BMPs through Modelling.” Ecological Modelling 353 (April 2015). Elsevier B.V.: 139–49. doi:10.1016/j.ecolmodel.2016.10.018.

Marinaki, Magdalene, and Markos Papageorgiou. 2003. “Linear-Quadratic Regulators Applied To Sewer Network Flow Control.” European Control Conference (ECC), 2407–2412.

McGarity, Arthur E. 2012. “Storm-Water Investment Strategy Evaluation Model for Impaired Urban Watersheds.” Journal of Water Resources Planning and Management 138 (2): 111–24. doi:10.1061/(ASCE)WR.1943-5452.0000157.

Middleton, John R, and Michael E Barrett. 2008. “Water Quality Performance of a Batch-Type Stormwater Detention Basin.” Water Environment Research : A Research Publication of the Water Environment Federation 80 (2): 172–78. doi:10.2175/106143007X220842.

Minnesota Stormwater Steering Committee. 2008. The Minnesota Stormwater Manual. 2nded. Vol. 2. Minnesota Pollution Control Agency.

Mobley, John T., and Teresa B. Culver. 2014. “Design of Outlet Control Structures for Ecological Detention Ponds.” Journal of Water Resources Planning and Management 140 (11): 4014031. doi:10.1061/(ASCE)WR.1943-5452.0000420.

Mobley, John T., Teresa B. Culver, and Thomas E. Hall. 2014. “Simulation-Optimization Methodology for the Design of Outlet Control Structures for Ecological Detention Ponds.” Journal of Water Resources Planning and Management 140 (11): 4014031. doi:10.1061/(ASCE)WR.1943-5452.0000420.

Montaseri, Majid, Mahdi Hesami Afshar, and Omid Bozorg-Haddad. 2015. “Development of Simulation-Optimization Model (MUSIC-GA) for Urban Stormwater Management.” Water Resources Management 29 (13): 4649–65. doi:10.1007/s11269-015-1082-z.

Needham, By Jason T, David W Watkins Jr, Jay R Lund, Associate Members, and S K Nanda. 2000. “L INEAR P ROGRAMMING FOR F LOOD C ONTROL AND D ES M OINES R IVERS” 126 (June): 118–27.

Nicolini, Matteo, and Luigino Zovatto. 2009. “Optimal Location and Control of Pressure Reducing Valves in Water Networks.” Journal of Water Resources Planning and Management 135 (June): 178–87. doi:10.1061/(ASCE)0733-9496(2009)135:3(178).

Obropta, Christopher C., and Josef S. Kardos. 2007. “Review of Urban Stormwater Quality Models: Deterministic, Stochastic, and Hybrid Approaches.” Journal of the American Water Resources Association 43 (6): 1508–23. doi:10.1111/j.1752-1688.2007.00124.x.

Ocampo-Martinez, Carlos, Ari Ingimundarson, Vicen?? Puig, and Joseba Quevedo. 2008. “Objective Prioritization Using Lexicographic Minimizers for MPC of Sewer Networks.” IEEE Transactions on Control Systems Technology 16 (1): 113–21. doi:10.1109/TCST.2007.899741.

Papa, Fabian, Barry J Adams, and Yiping Guo. 1999. “Detention Time Selection for Stormwater Quality Control Ponds.” Canadian Journal of Civil Engineering 26 (1): 72–82. doi:10.1139/l98-046.

Perez-Pedini, Cristina, James F Limbrunner, and Richard M Vogel. 2005. “Optimal Location of Infiltration-Based Best Management Practices for Storm Water Management.” Journal of Water Resources Planning & Management 131 (6): 441–48. doi:10.1061/(ASCE)0733-9496(2005)131:6(441).

Petrucci, Guido. 2017. “Should We Trust Build-up / Wash-off Water Quality Models at the Scale of Urban Catchments ?” 108: 422–31. doi:10.1016/j.watres.2016.11.027.

Pleau, M., G. Pelletier, H. Colas, P. Lavallee, and R. Bonin. 2001. “Global Predictive Real-Time Control of Quebec Urban Community’s Westerly Sewer Network.” Water Science and Technology 43 (7): 123–30.

Pleau, Martin, Hubert Colas, Pierre Lavallee, Genevieve Pelletier, and Richard Bonin. 2005. “Global Optimal Real-Time Control of the Quebec Urban Drainage System.” Environmental Modelling and Software 20 (4 SPEC. ISS.): 401–13. doi:10.1016/j.envsoft.2004.02.009.

Pleau, Martin, Christiane Marcoux, and Hubert Colas. 1998. “The Design of Sewer Networks: A New Approach Based on the Minimization of the Construction Cost.” In Nouvelles Technologies En Assainissement Pluvial. Conference International.

Pleau, Martin, Geneviève Pelletier, Hubert Colas, Pierre Lavallée, and Richard Bonin. 2002. “RELIABILITY AND ROBUSTNESS IN REAL-TIME CONTROL APPLICATIONS Martin.” Journal of Chemical Information and Modeling 53 (4798): 160. doi:10.1017/CBO9781107415324.004.

Pleau, Martin, Genevieve Pelletier, Christiane Marcoux, Charles Meunier, and Richard Bonin. 2000. “REAL-TIME CONTROL FOR CSO MANAGEMENT : QUEBEC URBAN COMMUNITY SYSTEM STARTUP.” In 29th Annual WEAO Technical Symposium and OPCEA Exhibition, Hamillton, Canada, 16–28. Hamilton. doi:10.1017/CBO9781107415324.004.

Propato, M. 2006. “Contamination Warning in Water Networks: General Mixed-Integer Linear Models for Sensor Location Design.” Journal of Water Resources Planning and Management-Asce 132 (4): 225–33. doi:10.1061/(ASCE)0733-9496(2006)132:4(225).

Rauch, W, and P Harremoës. 1999. “Genetic Algorithms in Real Time Control Applied to Minimize Transient Pollution from Urban Wastewater Systems.” Water Research 33 (5): 1265–77. doi:10.1016/s0043-1354(98)00304-2.

Regneri, Mario. 2014. “Modeling and Multi-Objective Optimal Control of Integrated Wastewater Collection and Treatment Systems in Rural Areas Based on Fuzzy Decision-Making Technischen Universität Graz.” Technischen Universität Graz.

Regneri, Mario, Kai Klepiszewski, Manfred Ostrowski, and Peter a Vanrolleghem. 2010. “Fuzzy Decision Making for Multi-Criteria Optimization in Integrated Wastewater System Management.” Proceedings of the 6th International Conference on Sewer Processes and Networks, no. 2008. http://modeleau.fsg.ulaval.ca/fileadmin/modeleau/documents/Publications/pvr941.pdf.

Saber-Freedman, Noah. 2016. “A Data-Driven Decision Model for Combined Sewer Overflow Management Using the Low-Impact Development Rapid Assessment Method.” Journal of Chemical Information and Modeling 53 (9): 1689–99. doi:10.1017/CBO9781107415324.004.

Sebti, Anas, Saad Bennis, and Musandji Fuamba. 2013. “Cost Optimization of Hydraulic and Structural Rehabilitation of Urban Drainage Network.” Journal of Infrastructure Systems 20 (3): 1–10. doi:10.1061/(ASCE)IS.1943-555X.

Shammaa, Y, D Z Zhu, L L Gyürék, and C W Labatiuk. 2002. “Effectiveness of Dry Ponds for Stormwater Total Suspended Solids Removal.” Canadian Journal of Civil Engineering 29 (2): 316–24. doi:10.1139/l02-008.

Shamsudin, Supiah, Salisu Dan, Azmi Aris, and Zulkifli Yusop. 2014. “Optimum Combination of Pond Volume and Outlet Capacity of a Stormwater Detention Pond Using Particle Swarm Optimization.” Urban Water Journal 11 (2): 127–36. doi:10.1080/1573062X.2013.768680.

TetraTech. 2016. “Introduction to Csoftfile:///C:/Users/shishesh/Documents/PhD Project/41114%2528371%2529258 – Copy.pdffile:///C:/Users/shishesh/Documents/PhD Project/41114%2528371%2529258 – Copy.pdf.”

Tobergte, David R., and Shirley Curtis. 2013. “Real Time Control for CSO Management.” Journal of Chemical Information and Modeling 53 (9): 1689–99. doi:10.1017/CBO9781107415324.004.

Travis, Quentin B, M Asce, Larry W Mays, and F Asce. 2008. “Optimizing Retention Basin Networks.” Journal of Water Resources Planning and Management 134 (5): 432–39. doi:10.1061/͑ASCE͒0733-9496͑2008͒134:5͑432͒.

Tung, Yeou-Koung. 1988. “Multi-Objective Detention Basin Design in Urban Drainage Systems – Tradeoff Between Risk and Cost.” Water Resources Management 2: 57–62.

Unver, Olcay I., and Larry W. Mays. 1990. “Model for Real-Time Optimal Flood Control Operation of a Reservoir System.” Water Resources Management 4 (1): 21–46. doi:10.1007/BF00429923.

Vanrolleghem, P. A., L. Benedetti, and J. Meirlaen. 2005. “Modelling and Real-Time Control of the Integrated Urban Wastewater System.” Environmental Modelling and Software 20 (4 SPEC. ISS.): 427–42. doi:10.1016/j.envsoft.2004.02.004.

Verdaguer, M., N. Clara, O. Gutiérrez, and M. Poch. 2014. “Application of Ant-Colony-Optimization Algorithm for Improved Management of First Flush Effects in Urban Wastewater Systems.” Science of the Total Environment 485–486 (1). Elsevier B.V.: 143–52. doi:10.1016/j.scitotenv.2014.02.140.

Vezzaro, L., M. L. Christensen, C. Thirsing, M. Grum, and P. S. Mikkelsen. 2014. “Water Quality-Based Real Time Control of Integrated Urban Drainage Systems: A Preliminary Study from Copenhagen, Denmark.” Procedia Engineering 70. Elsevier B.V.: 1707–16. doi:10.1016/j.proeng.2014.02.188.

Vezzaro, Luca, and Morten Grum. 2014. “A Generalised Dynamic Overflow Risk Assessment (DORA) for Real Time Control of Urban Drainage Systems.” Journal of Hydrology 515. Elsevier B.V.: 292–303. doi:10.1016/j.jhydrol.2014.05.019.

Wang, Fuxing, Oliver C. Saavedra Valeriano, and Xinguo Sun. 2013. “Near Real-Time Optimization of Multi-Reservoir during Flood Season in the Fengman Basin of China.” Water Resources Management 27 (12): 4315–35. doi:10.1007/s11269-013-0410-4.

Wang, Jian-Ping, Yong-Zhen Chen, Xue-Wu Ge, and Han-Qing Yu. 2007. “Optimization of Coagulation–flocculation Process for a Paper-Recycling Wastewater Treatment Using Response Surface Methodology.” Colloids and Surfaces A: Physicochemical and Engineering Aspects 302 (1–3). Taylor & Francis: 204–10. doi:10.1016/j.colsurfa.2007.02.023.

Watkins, David W, Dustin J Jones, and David T Ford. 1999. “Flood Control Optimization Using Mixed-Integer Programming David W. Watkins, Dustin J. Jones, and David T. Ford.” In 26th Annu. Water Resour. Plng. and Mgmt. Conf., ASCE, Reston, Va, 1–8.

Yazdi, J, E H Lee, and J H Kim. 2014. “Stochastic Multiobjective Optimization Model for Urban Drainage Network Rehabilitation.” Journal of Water Resources Planning and Management 141 (Shrestha): 1–11. doi:10.1061/(ASCE)WR.1943-5452.0000491.

Yeh, Chao-Hsien, and John W Labadie. 1997. “MULTIOBJECTIVE WATERSHED-LEVEL PLANNING OF STORM WATER DETENTION SYSTEMS.” Journal of Water Resources Planning and Management 123 (6): 336–43.

Yu, Jianjun, Xiaosheng Qin, A M Asce, Yee Meng Chiew, M Asce, Rui Min, and Xiling Shen. 2017. “Stochastic Optimization Model for Supporting Urban Drainage Design under Complexity” 143 (9): 1–10. doi:10.1061/(ASCE)WR.1943-5452.0000806.

Zamani Sabzi, Hamed, Delbert Humberson, Shalamu Abudu, and James Phillip King. 2016. “Optimization of Adaptive Fuzzy Logic Controller Using Novel Combined Evolutionary Algorithms, and Its Application in Diez Lagos Flood Controlling System, Southern New Mexico.” Expert Systems with Applications 43. Elsevier Ltd: 154–64. doi:10.1016/j.eswa.2015.08.043.

Zoltay, Viktoria I, A M Asce, Richard M Vogel, M Asce, Paul H Kirshen, M Asce, Kirk S Westphal, and M Asce. 2010. “Integrated Watershed Management Modeling : Generic Optimization Model Applied to the Ipswich River Basin.” Journal of Water Resources Planning and Management 136 (September): 566–75. doi:10.1061/(ASCE)WR.1943-5452.0000083 CE.