Tourism for Surf/Marsh Fishing in Coastal Louisiana, USA

Abstract

We apply the Kuhn-Tucker model to understand recreational behavior for surf/marsh fishing trips to six sites in coastal Louisiana. Results show statistically significant effects of individual’s demographic characteristics and site physical and environmental characteristics. The closure of three most used recreational sites (Grand Isle, Elmer’s Island, and Port Fourchon) causes welfare reduction in the amount ranging from $456-$1,611 per traveler. The welfare gain resulting from $20 reduction in travel cost (for example due to gasoline price reduction) is found to be $299 per traveler. However, increase in the recreational site entrance fee causes welfare losses. This study has implications for site closure and welfare loss such as that resulted from Deep Horizon Oil Spill that closed many Louisiana coastal recreational sites for about one year (May 7, 2010 to June 15, 2011) and Elmer’s Island beaches which were temporarily restricted for fishing access during Caminada Headland restoration project construction in 2016.

Keywords: Kuhn-Tucker model, recreation demand, surf/marsh fishing, site closure, entrance fee increase

1. Introduction

The travel cost model (TCM) is a demand-based model used to estimate gain/loss economic use value resulting from changes in environmental quality or elimination of an existing recreational site. The assumptions of TCM are that the expenditures of time and travel cost that traveler/tourist incur to visit a site represent the ‘price’ of access to the site. Surveys (on site or off site) are used to collect data on the number of visits that a traveler/tourist makes to a site and on the cost of gaining access (Garrod and Willis, 1999). The willingness to pay (WTP) value to visit the site can be estimated based on the number of trips that recreationists make at different travel costs and it is assumed that changes in travel cost will change the number of visits (Pascoe et al., 2014). The main idea of the TCM is to exploit the variation across people in visits and travel cost to reveal the demand for a recreational site (Parson, 2003).

The traditional and simplest travel cost model is a single site model, which is used for assessing the recreational value of single site and works like conventional downward sloping demand functions (Witt and Witt, 1995). The demand function slopes downward if trips decline with distance to the recreational-site. A single-site demand model is useful and can be easily performed by using aggregate data to predict current demand for a site (Parson, 2003). However, with a single site model, it is difficult to statistically identify the relationship between site visitation and site quality for travelers; since the quality of a single site does not vary across the sample of travelers and thus all people face the same site quality. Another issue is that many recreation sites are likely to have close substitutes, the non-market value of a site of interest will hinge heavily on the existence and characteristics of substitute sites, the effect of which is not well captured by a single site model. Therefore, the single site model can only be used to estimate the recreational value for a single destination and is unable to incorporate all relevant substitute sites.

When recreationists have a choice to visit a site from a set of multiple sites available with different site characteristics, a multiple site model is preferred. The random utility maximization (RUM) model, which is based on the random utility theory, is the most widely used multiple site model (Ben-Akiva and Lerman, 1985). The RUM model assumes that individuals will choose a single site out of all possible alternatives to maximize their utility. The RUM model requires information on all available sites, their quality characteristics, and the travel costs to each site. This approach is the most complicated and data intensive among different travel cost models. On a given choice occasion, the RUM model is an effective tool to estimate benefits for specific characteristics or quality changes of a site. However, the RUM framework is insufficient to estimate the substitute effects, which is that the demand for alternatives decreases when the travel cost decreases for a site. Since the foundation of RUM model is based on the utility maximization theory, the unit of choice in the model is a single site selection. A simple RUM model captures only one aspect of the recreation demand problem and is not suited for modeling behavior over a longer time horizon.

The Kuhn–Tucker (KT) model, which was discussed originally by Hanemann (1978) and developed by Wales and Woodland (1983) and Lee and Pitt (1986), has become the preferred model for analyzing the site and frequency selection and associated corner solutions (i.e. the fact that individuals who do not visit all sites). The KT model relies on a single structural framework and uses the utility maximization problem directly, which simultaneously incorporates both site selection and participation decisions with corner solutions and has been proposed as a means of dealing with corner solutions. Also, the KT model embodies the substitutability between recreation sites and sites’ attributes, and allows consistent welfare analysis (Sánchez et al., 2016). Thus, it is possible to value the data including individuals’ various patterns of site selection (some sites are not visited, some sites are visited more than once). This paper applies the KT model to estimate the recreational demand for surf/marsh fishing in coastal Louisiana. Understanding the demand for these recreation sites allows one to better evaluate -recreational fishing regulations and state park policies change.

The remainder of this paper proceeds as follows. The next section provides background on coastal tourism in Louisiana. Section 3 provides a brief overview of the KT model following Phaneuf et al. (2000). Section 4 describes survey design, the treatment of the travel cost, and summarizes some sample characteristics. Section 5 reviews the empirical corner solution estimation process. Model results are presented in section 6 while section 7 provides conclusions with some recommendations for further research.

2. Tourism in Coastal Louisiana

Louisiana’s coastal area provides a variety of economic, ecological, cultural and recreational values to residents of the state. Louisiana coastal area is one of the most productive ecosystems that supplies an abundance of fisheries resources in the United States. Benefits of coastal wetlands include flood control, shoreline protection, carbon storage, the provision of biological diversity, and supporting fishery and ecotourism industries (Costanza et al., 1997; Pennings and Bertness, 2001). Tourism is the second largest coastal industry in the U.S. Gulf Coast ranking only behind oil production.

Tourism is a major contributor to Louisiana’s economy. Over 87,000 people work at tourism industry. Louisiana’s nickname “Sportsman’s Paradise” implies that there are many outdoor activities available for recreationists. In 2014, Louisiana received a total of $10.7 billion from domestic traveler including both state residents and out-of-state visitors and traveler spending directly supported 107,600 jobs in Louisiana (CUTD, 2015).

Unlike other states in the United States, Louisiana’s coastal area is less suitable for sunbathing type of beach recreation. Surf/marsh recreational fishing is one of the main attractions in the state. Richardson and Scott (2004) reported that almost 650,000 recreational fishermen chose to take a saltwater fishing trip in Louisiana. Of these 650,000 recreational fishermen, almost 100,000 were from out-of-state, while just over 66,000 were from non-coastal parishes in Louisiana in 2002. Coastal Louisiana is the favorite place for more than half a million anglers to catch fish. Many fishing locations are available around the coastal area. For example, Grand Isle is Louisiana’s only inhabited barrier island and known for its world-class fishing and the multitude of fishing rodeos. It hosts these activities throughout the summer weekends and brings as many as 20,000 visitors (Johnson, 2016). All these visitors support a recreational fishing industry which generates a multitude of jobs, income, and sales across the state. Thus, recreational fishing activity plays an import role in attracting people to visit Louisiana and also is important to the state’s economy.

3. Theoretical Model

3.1 The KT model

The KT model uses the Kuhn–Tucker conditions directly and is the most appropriate model for multiple site analyses. Under the utility maximization problem, the KT model treats a visited site as an interior solution and a non-visited site as a corner solution. This model is suitable for seasonal recreation data for corner solution. Phaneuf et al. (2000) present the first full application of corner solution models to the analysis of Great Lakes fishing in Wisconsin. von Haefen et al. (2004) applied KT model to the analysis of beach recreation in the mid-Atlantic region. As discussed by Phaneuf et al. (2000), the formulation of the Kuhn-Tucker model assumes that consumer preferences can be represented by a random utility function and consumers maximize utility over a season subject to a budget constraint and non-negativity constraints. The theoretical basis of KT follows the random utility maximization and is given by:

max U(x,z,q,β,ε)	(1)
s.t. px+z=y,     z>0, xj>0,  j=1, 2,⋯,M

where

U(∙) is a continuously differentiable, strictly increasing and quasi-concave utility function of (x,z),

x=(x1,⋯,xM )’is a vector of the number of trips to each site,

z is the numeraire whose price is normalized to one and represents spending on all other goods,

q=(q1,⋯,qM )’ is a vector of the corresponding qualities,

β=(β1,⋯,βM )’ is a vector of parameters that may vary randomly across individuals to capture unobserved heterogeneity,

ε=(ε1,⋯,εM )’ is a vector of error term across individuals and sites,

p=(p1,⋯,pM )’ is a vector of price (travel cost, access fees, etc.) to visit each site,

y denotes individual’s annual income and

M is the total number of recreation sites.

Consumers maximize utility subject to budget and nonnegativity constraints. The first-order conditions for maximization take the form as follows:

Ujx, y-px,q,β,εUzx, y-px,q,β,ε≤pj,     xj≥0,     xjUj-pjUz=0,  j=1,⋯,M,	(2)
where Uj=∂U∂xj and Uz=∂U∂z.

These equations show that for an interior solution (positive trips), the marginal rate of substitution between the trip to the site and other spending becomes equal to the cost to visit the site. For corner solution (zero trip x=0), the marginal rate of substitution between the trip to the site and other spending falls below the cost to the site. The first-order condition in equation (2) can be rewritten as follows:

εj≤gjx,p,y,q,β,     xj≥0,     xjεj-gj=0,      j=1,⋯,M,

(3)

where

gj=(x,p,y,q,β) is the solution to the equation

xjUj-pjUz=0. The probability that the number of trips is positive (interior solution) is

Prxj=x=Pr(εj=gj). The probability that the number of trips is zero (corner solution) is

Prxj=0=Pr(εj

∫-∞gk+1⋯∫-∞gMfϵ(g1,⋯,gk,εk+1,⋯,εM×JKdεk+1,⋯,εM,

(4)

where

JK denotes the Jacobian for the transformation from

ε to

(x1,⋯,xk,εk+1,⋯,εM )’.

β can be estimated by specifying the distribution of ε.

3.2 Welfare calculation

Indirect utility function V(∙) can be derived from the utility maximization problem (1). For an individual, willingness to pay (WTP) or compensating variation (CV) can be defined as the amount of income that compensates for a change in price and/or quality (from (p0,q0) to p1,q1) in the public good. If the initial and new quality levels are such that q1>q0, then (CV>0)and the equation is given by:

vp0,q0,y,β,ε=vp1,q1,y-CV,β,ε.

(5)

Equation (5) indicates that the compensating variation will depend on the arguments of the indirect utility function. This implies that

CV(p0,q0,p1,q1,y,β,ε)  is a random variable, since it depends on the unknown value for ε. The CV can be defined with the expenditure function e(∙)and given it by:

CV=ep0,q0,U0-ep1,q1,U0=y-ep1,q1,U0p0,q0,y,β,ε,β,ε,

(6)

where

e∙ is the expenditure function and

U0 is the original level of utility.

The error terms

ε in equation (6) are not observed and the function

e∙ is not fully known to researchers, which implies that

CV is a random variable. Therefore a closed form solution does not exist and, only the expected value of compensating variation (E(CV)) can be computed using a numerical approach (Whitehead et al., 2010). Phaneuf et al. (2000) proposed the first strategy to measure CV and Phaneuf and Siderelis (2003) detailed the procedure on how to obtain CV from equation (5). One possibility is to draw the error vector ε from conditional sampling.

The maximization conditions in equation (3) suggest that depends on whether the site is visited or not. Therefore,

εj=gj for visited sites and

εj

εj=-ln⁡-ln⁡exp⁡-exp⁡giv*U*v,

(7)

here, is a random draw from (0,1) uniform distribution.

Based on sampled value of the error and the number of trips, the first step is to solve the value of indirect utility function for each condition (before and after a change in travel cost and site quality) and select the optimum value (consumption x^∗ and z^∗). The next step consists of repeating the process for multiple draws of the error and then the averaging CV estimates over the draws of the error to obtain E(CV).

von Haefen et al. (2004) significantly refine Phaneuf et al.’s approach and develop a more efficient expenditure function-based approach to calculate CV from equation (6). Under the assumption that consumer preferences are additively separable in each element of x and z, the KT condition of the expenditure minimization problem of individuals is given by:

Uj≤Uzpj,     xj≥0    ∀j    j=1,⋯,M,

(8)

u̅=∑kMukxk+uz(z).

(9)

Therefore, under the additive separability condition, the values of x and z that minimize expenditure can be obtained by using the following numerical bisection algorithms (von Haefen et al., 2004).

1) At iteration , set zai=(zli-1+zui-1)/2. To initialize the algorithm, set zl0=0 and zu0=uz-1(U̅-∑uj(0)).

2) Conditional on zai, solve, for xi  using the KT condition (equation (8)). Solve for ũi=U(xi, zai) using xi and equation (9).

3) If Ũi zli=zai and zui=zui-1. Otherwise, set zli=zli-1 and zui=zai.

4) Iterate until | zli-zui|≤ where is arbitrarily small.

The optimal solutions x* and z* can be found from the above algorithm. Then the expenditure needed to achieve the baseline utility under the changed condition can be calculated and the CV can be calculated from equation (6) using the expenditure.

4. Data

The empirical application of the KT model focuses on recreational demand (surf/marsh fishing) in coastal Louisiana. Data come from the internet and intercept surveys of recreationists conducted in 2003 by researchers supported by the Louisiana Sea Grant College Program at Louisiana State University. Although data used are 14 years old, questions used and recreational sites considered in the survey are the same and information obtained is as relevant today as then.

We use observations collected from the same survey questionnaire posted online and collected from site intercept. The Internet survey was hosted on a Web-server in the LSU Department of Agricultural Economics and Agribusiness, which was available to respondents from May 15 to July 31, 2003. Announcements were made in 28 media outlets to attract a diverse range of participants. Notices were made via direct email, Websites, newspapers, newsletters, magazines, and radio programs. A total of 2,486 responses were received from an online survey posted on the web server. In addition to the internet survey, an in-person survey, or “intercept” survey, was conducted at Grand Isle State Park and Holly Beach. To encourage participation in the intercept survey, a commemorative cap was provided to all who fully completed the survey. The intercept survey was conducted within 42 days using a series of multi-day trips to the sites during June and July 2003. A total of 203 observations was obtained from intercept survey. The survey provides detailed information about the number and destination of recreational activities, the type of preferred activities, preference over different site quality, number of trips, travel time, trip expenses, and the sociodemographic characteristics of the survey respondents. Descriptive statistics of variables used in the analyses from online and intercept survey were statistically insignificant, so we pooled data from both sources in the analyses. Since this study focuses on the first preferred activity (surf/marsh fishing), the online and intercept data were sorted so that only those with surf/marsh fishing as their primary purpose of visit are included. Thus, a total of 1,111 completed observations were used for economic impact and demand analysis. An overwhelming majority (95%) of observations in this study are recreationists from within Louisiana. The dataset can be used for the KT model to understand the site choice decision. Given that online and intercept survey values are not significantly different, we believe the dataset is representative enough to understand the recreational behavior of visitors in coastal Louisiana. This survey asks individuals on their location choice (recreation site) for their most favorite coastal activities. Six most popular recreational sites in coastal Louisiana were chosen for this analysis (Figure 1). These sites are: Site 1: Cocodrie; Site 2: Elmer’s Island (EL); Site 3: Port Fourchon; Site 4: Grand Isle (GI); Site 5: Leeville, and Site 6: Venice.

On average, travel cost ranges from a low $62 to a high $320 per trip among all sites. The travel cost is included to capture the valuation of other attributes. Cesario and Knetsch (1970) suggest converting time cost to monetary value and combining it with the travel cost as a measure of the full cost of travel to a recreation site. Accordingly, the price of a trip to each of the fishing sites consists of both the direct cost of getting to the site (round-trip travel cost) and the indirect cost (opportunity cost) of the travel time. Round-trip direct travel cost is computed for each destination and each individual by multiplying the number of round-trip miles for a given individual destination combination by the average cost per mile (51.7 cents) for the vehicle driven (USDT, 2014). The cost of the travel time was constructed using one-third of the individual’s wage rate as a measure of the hourly opportunity cost of recreation time (Cesario, 1976). The calculation of price is given as the following:

pj=dist*2*$0.517mile+(onsitetime+drivingtime*2)*$14.8hour*1/3,

(10)

where, the price of visiting a destination

pj represents the sum of the direct and indirect travel cost for individual i. dist represents the distance from the address of the individual to the destination, $0.517/mile stands for the average cost per mile for vehicle driven in 2003 in USA. The travel time is separated out into the components of travel time and on-site time (Smith et al., 1983; Shaw, 1992; and McConnell, 1992). As the average wage rate was $14.8/h in Louisiana in 2003 (LAWDL, 2003), we assume $14.8/h ×1/3 to be the opportunity cost. Both round trip distance from each respondent’s residence to each of the six sites and travel time is calculated using R software based on ggmap package.

The survey asks each respondent to choose from six preferred recreation alternatives. To characterize demand to recreation sites, total annual household income was collected. We also use a dummy variable to indicate ownership of a boat. Descriptive statistics for individual attributes are shown in Table 1. Most respondents in this sample are male and the average respondent is 42 years old. This table also shows that the average annual household income is $67,147 and average work hour is 41 hours per week.

Each choice alternative is described in terms of ten types of quality attributes, which are used to characterize the recreation sites. The presence of environmental attributes is likely to influence the recreation decision and is important in modeling demand function for recreational choice. Levels of importance of those attributes in choosing to visit the site are measured by using a five-point Likert preference scale with five being very important and one being not important at all. Total catch of fish per trip (TCPT) might be an important environmental factor affecting recreation decision. The level of pollution (LP) is another possible important quality attribute of each site because a degraded site reduces the probability of visit.  Other environmental characteristics may also have potential impact on the decision of recreation fishing trip, and those include: ease of access to site (EAS), low human congestion (LHC), abundant wildlife (AW), camping facility (CF), interpretive signs (IS), level of development (LD), rules and regulations (RR), and nearby food and lodging (NFL).

Descriptive statistics of observed trips for each site are shown in Table 2. On average, individuals visited two of the available sites in 2002 and took an average of 12 total trips to the site. The median number of total trips to the region is zero with range zero to 70. Many respondents visited only a few sites during the year suggesting a corner solution for site visits. Most of the respondents indicated that environmental amenities were an important consideration when visiting coastal recreation sites. Concerns about pollution and site access were of greatest importance to visit a recreational site amongst all respondents, with the Likert scale value (1 to 5, with 5 being the best) averaging 4.57 and 4.22, respectively. On the other hand, the provision of interpretive signage and camping facility were ranked only somewhat important and of little importance, with values averaging 2.10 and 2.09, respectively. These values suggest that the average respondent in this survey favors recreation sites with low level of pollution and high levels of environmental integrity. Such preferences are consistent with the findings of other studies in which coastal tourists were found to have high preferences for environmental amenities (Kenchington, 1993; Leatherman, 1997; Oh et al., 2009; Oh, 2010; and Pueyo-Ros et al., 2016).

5. Model Specification

The estimation of the KT model requires the specification of the direct utility function and the error term. Following von Haefen et al. (2004), the additively separable utility function can be specified as:

U=∑j=16Ψjs,εjln∅(qj)xj+θ⁡+1ρzρ    j=1,…, 6,

(11)

where,

Ψjs,εj=exp⁡δ0+δAGEAGE+δHOURSHOURS+δBOATBOAT+δGENDERGENDER+εj,  j=1,⋯,6, ∅(qj)=exp⁡βTCPTTCPT+βEASEAS+βLHCLHC+βLOPLOP+βAWAW, θ=exp⁡(θ*), ρ=1-exp⁡ρ*, z=y-p’x, μ=exp⁡(μ*), εj~EVμ.

(12)

In equation (11) and (12),

xj is the number of trips taken to the j^th site, z is the consumption of numeraire (spending on all other goods), s represents socio-demographic variables, qj denotes the site-specific quality variables, εj represent the random error vector, and θ is a translating parameter (the influences on utility regardless of the number of trips) to be estimated. The terms, Ψjs,εj and ∅(qj), are constructed to be a positive aggregator functions for individual-specific variables and site characteristics, respectively.

δ’s  and β’s are the parameters to be estimated. AGE is individual’s age, HOURS stands for the work hour per week, BOAT represents the ownership of boat (boat=1), MALE represents the gender (male=0), TCPT is total catch of fish per trip, EAS is ease of access to site, LHC represents low human congestion, LP stands for the level of pollution, and AW represents abundant wildlife.

Because unvisited sites do not influence utility, weak complementarity between the recreation sites and their associated quality measures is satisfied. Maximization of equation (11), the first-order Kuhn-Tucker conditions with respect to x and z leads to the following equations:

y-∑j=16pjxjΨjs,εj∅qjxj∅qj+θ≤pj ,    j=1,⋯,6.

(13)

Substituting equation

Ψjs, εj into equation (13) and solving for the error term in each equation allows the first-order utility maximization conditions to be rewritten as:

εj≤gj,     j=1,⋯,6,

(14)

here,

gj=ln⁡pj-ln⁡∅qj+ln⁡xj∅qj+θ-ρ-1ln⁡y-∑j=16pjxj-δ’s.

(15)

To estimate parameters, assuming the error vector εj is identically and independently distributed as Type-I extreme value distribution (Gumbel distribution) for each site. The cumulative distribution function of εj is defined as F(εj)=exp⁡[-exp⁡-εj/v]. Let v be a scale parameter and normalized to one and let I be an indicator function such that I=1 if  xi>0. Then individual i’s log-likelihood function is given by (Phaneuf and Sidereslis, 2003):

llj=-∑j=16I*gjv-∑j=16exp⁡[-gjv]-∑j=16I*ln⁡v+ln⁡J ,

(16)

here, J is the Jacobian transformation from ε to x and the Jacobian matrix are calculated using equation (15).

6. Results

6.1 Parameter estimates

Table 3 shows the results from the KT model. All the signs of the individual characteristic variable are as expected. For the variables AGE and HOURS, the signs are negative and statistically significant at a 5% level, which suggest that older people take fewer trips, and people who work more hours per week spend less time on recreation trips. The variable BOAT is not statistically significant and provide no contribution to the model, which might imply that most of the recreation fishing sites are easily accessible without using a boat. The sign for GENDER variable is negative and statistically significant at a 10% level. This result suggests that female will make less fishing trips to all sites.

All of the parameters of environmental characteristic variable have the expected signs with the exception of the coefficient on total catch of fish per trip. The negative and significant TCPT variable is surprising. A plausible explanation for this finding is that the importance of TCPT is not a significant factor in the consideration of recreation trip but it might be an important factor for commercial or sports fishing activities. An individual may take more trips if he/she places lower importance to TCPT.

The variable level of pollution (LOP) is statistically significant at a 1% level with a negative sign, which suggests that if an individual places higher importance to LOP, he/she would take less trips. Low human congestion variable is not significant and provide no information in the model. The results also show that ease of access to site and abundant wildlife are significant determinant of choice as measured by using a five point Likert scale, suggesting that visitors take more trips to sites if he/she place higher importance to EAS and AW.

6.2 Policy analysis

To calculate welfare change, this paper applies the conditional approach to welfare measurement developed by von Haefen et al. (2004). In the following, we simulate welfare changes in five policy scenarios. The policy scenarios analyzed include:

Scenario 1 represents the situation resulting in a closure of Grand Isle site

Scenario 2 represents the situation resulting in a closure of Elmer’s Island site

Scenario 3 represents the situation resulting in a closure of Port Fourchon site

Scenario 4 represents the situation in which the total travel cost decreases by $20 in all sites possibly because of gasoline price reduction

Scenario 5 represents the situation where a $10 access fee is charged to visit Grand Isle

While these scenarios are hypothetical, they do have policy implications. Grand Isle, located on a barrier island of the same name in the Gulf of Mexico, is at the mouth of Barataria Bay where it meets the Gulf of Mexico. Elmer’s Island, owned and maintained by the state of Louisiana, is a 230-acre tract of barrier beachfront located on the southwestern tip of Jefferson Parish and located directly across Caminada Pass from Grand Isle, LA. The Caminada Headland is a 13-mile-long undeveloped beach running from the Belle Pass eastward to Caminada Pass at the end of Elmer’s Island and has experienced significant shoreline erosion and land loss over the last 100 years. To address this issue, the State of Louisiana and Federal agencies proposed to restore the Headland shoreline (Caminada Headlands Beach and Dune Restoration) which occurred in two project increments. The Coastal Protection and Restoration Authority (CPRA) has acquired Coastal Impact Assistance Program (CIAP) and 2008 State Surplus funds for Increment I of the project. The Increment I was completed in December of 2014 and restored approximately 300 acres and six miles of beach and dune habitat. The Increment II was founded through the National Fish and Wildlife Foundation (NFWF) and was completed in March of 2017. The Increment II restored approximately 500 acres and seven miles of beach and dune habitat. Elmer’s Island was temporarily closed to all access during the construction of the Caminada Headland restoration projects. Recently, the Louisiana Department of Wildlife and Fisheries (LDWF) and the CPRA announced that vehicles are permanently prohibited on Elmer’s Island beaches. Port Fourchon is located on the southern tip of Lafourche Parish, Louisiana, on the Gulf of Mexico. It has been repeatedly impacted by hurricanes through its history. From the tropical cyclone report, on average, Grand Isle has been affected by tropical storms or hurricanes every 2.68 years (since 1877), with direct hits on average every 7.88 years. Port Fourchon was damaged by Hurricane Lily in October 2002. Likewise, 2005 Hurricane Katrina and 2008 Hurricane Gustav had significant impacts on Elmer’s Island and Grand Isle, which temporarily caused closure of these recreation sites.

The Deepwater Horizon oil spill began on 20 April 2010 in the Gulf of Mexico on the BP-operated Macondo Prospect. A total of 170 million gallons of oil and 200,000 metric tons of methane gas spilled into Gulf waters over two months, affecting nearly 1,000 miles of shoreline. Louisiana was the first state to be hit by the oil spill. As a result, all four segments of Fourchon Beach in Lafourche Parish, one section of Grand Isle Beach, and all four sections of Grand Isle State Park Beach in Jefferson Parish have been closed (Dorfman and Rosselot, 2011). Caffey and Paudel (2003) reported that at the historic annual visitation rate of 40,000 people to Elmer’s Island, it is estimated that a minimum of $750,000 in direct expenditures and $1,500,000 in economic activity were lost annually when Elmer’s Island was closed for a few years. In this analysis, the first three scenarios simulate the welfare loss that are most likely associated with potential tropical storm and oil spill such BP spill.[1]

Gas prices have fallen consistently since 2014 and will save the average American household $700 in 2015 according to U.S. government projections (EIA, 2015). The lower price of gasoline would decrease consumer’s travel cost. The fourth hypothetical policy scenario would be expected to have a potential impact on welfare gain for consumers. Most of the recreation fishing sites in coastal Louisiana are open access to public, and some sites only charge a few ($3) dollar entrance fee. Use of access fees to raise revenue is possible. In fact, Louisiana just increased the state park day time entrance fee to $3 effective March 1, 2017. The fifth policy scenario is expected to have a negative impact on traveler’s welfare.

Given the parameter estimates in Table 3, the compensating variation estimates are presented in Table 4. Table 4 shows the mean and robust standard error of individual seasonal welfare effects of the five policy scenarios with the expected signs. All estimates are statistically significant at 1% level. The closure of recreation sites contributes to a welfare loss. On average, the welfare impact of sites closure to per survey respondent is $1,611, $526, and $456 for Grand Isle, Elmer’s Island, and Port Fourchon, respectively. As expected, gasoline price drop (or other similar travel cost reduction by $20) would benefit on average $299 per travelers. For the last policy scenario, the potential welfare loss is $57 per person on average.

The average welfare measures can be used to estimate the aggregate welfare impacts under different policy scenarios. For example, based on the survey observations (N=1,111) and account for inflation, this research suggests an aggregate welfare loss values for sites closure are $2.35 million, $0.76 million, and $0.67 million in 2016 dollar for Grand Isle, Elmer’s Island, and Port Fourchon, respectively. An aggregate welfare gain is $0.43 million when the travel cost decreased by $20. In the case of a $10 access fee is charged to visit Grand Isle, the aggregate welfare loss is $0.08 million.^[2] From the Visit to Jefferson Parish 2015 Annual Report, a total of 52,405 people visited Grand Isle State Park in fiscal year 2013/2014. Thus, the aggregate welfare impacts can be substantially large if the population is based on an annual visitation from all six recreation locations.

7. Summary and Conclusions

The purpose of this paper was to understand travelers’ preference for surf/marsh fishing destinations. We, we employed an empirical application of the KT model to investigate the demand for surf/marsh fishing in coastal Louisiana. The KT model provides a consistent framework to estimate both small and large choice sets as well as welfare measurement (von Haefen et al., 2004). In the application of KT model to surf/marsh fishing recreation demand, we choose the first preferred activity (surf/marsh fishing) into six favorite coastal recreation sites: Cocodrie, Elmer’s Island, Grand Isle, Port Fourchon, Leeville, and Venice. Empirical results from our analyses support previous research indicating site physical and environmental characteristics play an import role when choosing among different coastal recreational destinations and mostly show consistency and statistically significant effect of individual’s demographic characteristics. Individual’s age and work hours per week significantly affect fishing trips. The importance of the level of pollution, ease of access to the site, and abundant wildlife also significantly affect site choice. However, the ownership of a boat variable and the environmental variable, low human congestion, are found to be insignificant. Total catch per trip is significant but with unexpected signs. Given most of the visitors are recreation oriented visitors, it is likely that they do not care about fish catch as much as commercial fishermen. Although the values from this research cannot be directly transferred in all other places/situations, it contributes to the travel cost literature and provides a component of indirect value for revealed preference analysis.

We estimated potential welfare losses associated with site closures. These site closures could be the results of tropical storms and other uncertainties such as coastal restoration projects or oil spill. We estimated potential welfare losses caused by the changes to the entrance fee that can be resulting from the State budget proposal. We also estimated potential welfare gains associated with changes in the gasoline price. Results show that the closures of a recreation site and increasing current park access fee reduce welfare. These policy analyses illustrated travelers’ willingness to accept/pay under different scenarios, which demonstrate the relationship between the effects of site closures, change of access fee and gasoline price and the recreation value. These results provide support for policymakers to evaluate current and potential recreational related policies. Empirical results presented here have potential implications for recreational demand policy and provide useful information for policymakers to improve recreation services and bring more benefits to the State.

The data used in the study come from the survey conducted in 2003, and the useable sample is a reduced subset of an original sample with over 2,000 observations. Some of the locations did suffer from 2005 Hurricane Katrina and 2010 BP Oil Spill, which caused these sites to temporarily close. These events represented a ‘shock’ to the system and did reduce welfare to travelers. Although data are 14 years old and some major events occurred since then, questions used and recreational sites considered in the survey are still the top recreational destinations and information obtained from the survey is as relevant today as then.  This paper revealed future research opportunities related to more comprehensive coastal recreational practice and policies.  Further study is needed to explore the statewide coastal demand associated with different recreational activities as a result of changes in site environmental characteristic. 

REFERENCES

Assessment, Deepwater Horizon Natural Resource Damage (ADHNRD). 2016. “Deepwater Horizon Oil Spill: Final Programmatic Damage Assessment and Restoration Plan and Final Programmatic Environmental Impact Statement.” Available at http://www.gulfspillrestoration.noaa.gov/sites/default/files/wp-content/uploads/Front-Matter-and-Chapter-1_Introduction-and-Executive-Summary_508.pdf (Accessed February 2017).

Louisiana Works Department of Labor (LAWDL). 2004. “Louisiana Employment and Wages Annual Report 2003.” Available at http://www.laworks.net/Downloads/OWC/2003owcareport.pdf (Accessed September 2016).

U.S. Department of Transportation (USDT). 2012. “National Transportation Statistics 2012.” Bureau of Transportation Statistics.

Ben-Akiva, Moshe E., and Steven R. Lerman. 1985. “Discrete Choice Analysis: Theory and Application to Travel Demand.” MIT Press, Cambridge.

Caffey, Rex H., Krishna Paudel, and Larry Hall. 2003. “Elmer’s Island Coastal Preference Survey.” Louisiana State University. Available at http://www.lsu.edu/seagrantfish/pdfs/Elmers_report.pdf (Accessed January 2017).

Center, US Travel Data (CUTD). 2015. “The Economic Impact of Travel on Louisiana Parishes, 2014.” Prepared for the Louisiana Office of Tourism, US Travel Data Center, Washington, DC.

Cesario, Frank J. 1976. “Value of Time in Recreation Benefit Studies.” Land economics, 52(1): 32-41.

Cesario, Frank J, and Jack L Knetsch. 1970. “Time Bias in Recreation Benefit Estimates.” Water Resources Research, 6(3): 700-704.

Costanza, Robert, Ralph d’Arge, Rudolf De Groot, Stephen Farber, Monica Grasso, Bruce Hannon, Karin Limburg et al. “The value of the world’s ecosystem services and natural capital.” Ecological Economics 25(1): 3-16.

Dorfman, Mark. and Kirsten S. Rosselot. 2011. “Testing the Waters: A Guide to Water Quality at Vacation Beaches.” Natural Resources Defense Council. Available at https://www.nrdc.org/sites/default/files/ttw2011.pdf (Accessed December 2016).

Energy Information Administration (EIA). 2015. “Monthly Energy Review, January 2015.” In.: Office of Energy Statistics, Washington DC. Available at http://www.eia.gov/totalenergy/data/monthly (Accessed September 2016).

Guy, Garrod, and Willis Kenneth. 1999. “Economic Valuation of the Environent: Methods and Case Studies.” Cheltenham: Edward Elgar Publishing.

Hanemann, Michael W. 1978. “A Methodological and Empirical Study of the Recreation Benefits from Water Quality Improvement.” Department of Agricultural and Resource Economics, University of California.

Johnson, Erik I. 2016. “Louisiana’s Coastal Stewardship Program 2015 Annual Report: Beach-nesting Bird Protection, Monitoring, and Community Outreach.” National Audubon Society, Baton Rouge, LA

Kenchington Richard. 1993. “Tourism in Coastal Environments – A Recreational Perspective.” Ocean & coastal management. 19(1): 1-16.

Krinsky, Itzhak, and Leslie A. Robb. 1986. “On Approximating the Statistical Properties of Elasticities.” The Review of Economics and Statistics: 68(4): 715-719.

Leatherman Stephen P. 1997. “Beach Rating: A Methodological Approach.” Journal of Coastal Research. 13(1): 253-258.

Lee, Lung-Fei., and Mark M. Pitt. 1986. “Microeconoetric Demand Systems with Binding Non- negativity Constraints: The Dual Approach.” Econometrica, 54(5): 1237-42.

McConnell, Kenneth E., and Ivar E. Strand. 1994. “The Economic Value of Mid and South Atlantic Sportfishing.” University of Maryland, Report to the USEPA and NOAA. Available at https://yosemite.epa.gov/ee/epa/eerm.nsf/vwAN/EE-0036B.pdf/$file/EE-0036B.pdf (Accessed January 2017).

Oh, Chi-Ok, Jason Draper, and Anthony W. Dixon. 2009.  “Assessing Tourists’ Multi-attribute Preferences for Public Beach Access.” Coastal Management 37(2): 119-135.

Oh, Chi-Ok. 2010. “Assessing Recreationists’ Economic Benefits and Their Transferability to Other Sites.” Leisure Sciences 32(2): 125-142.

Parsons, George R. 2003. “The Travel Cost Model, Chapter 9 in a Primer on Nonmarket Valuation. Edited by PA Champ, KJ Boyle and TC Brown.” In.: London, Kluwer Academic Publishing.

Pascoe, Sean, Amar Doshi, Quentin Dell, Mark Tonks, and Rob Kenyon. 2014. “Economic Value of Recreational Fishing in Moreton Bay and the Potential Impact of the Marine Park Rezoning.” Tourism Management, 41: 53-63.

Pennings, Steven C., and Mark D. Bertness. 2001. “Salt Marsh Communities.” Marine community ecology. 289-316.

Phaneuf, Daniel J., Catherine L. Kling, and Joseph A. Herriges. 2000. “Estimation and Welfare Calculations in a Generalized Corner Solution Model with an Application to Recreation Demand.” Review of Economics and Statistics, 82(1): 83-92.

Phaneuf, Daniel J., and Chris Siderelis. 2003. “An Application of the Kuhn-Tucker Model to the Demand for Water Trail Trips in North Carolina.” Marine Resource Economics: 1-14.

Pueyo-Ros, J. O. S. E. P., Anna Ribas, and Rosa M. Fraguell. 2016. “Recreational Uses and Motivations of Visitors in Seaside Wetlands of Costa Brava (Spain).” International Journal of Sustainable Development and Planning. 11(3): 385-395.

Richardson, James A., and Loren C. Scott. 2004. “The Economic Impact of Coastal Erosion in Louisiana on State, Regional, and National Economies.” Prepared for the Department of Natural Resources, State of Louisiana.

Sánchez, José J., Ken Baerenklau, and Armando González-Cabán. 2016. “Valuing Hypothetical Wildfire Impacts with a Kuhn–Tucker Model of Recreation Demand.” Forest Policy and Economics. 71: 63-70.

Shaw, Douglass W., and Paul Jakus. 1996. “Travel Cost Models of the Demand for Rock Climbing.” Agricultural and Resource Economics Review, 25: 133-42.

Smith, Kerry V., William H. Desvousges, and Matthew P. McGivney. 1983. “The Opportunity Cost of Travel Time in Recreation Demand Models.” Land economics, 59(3): 259-78.

von Haefen, Roger H., Daniel J. Phaneuf, and George R. Parsons. 2004. “Estimation and Welfare Analysis with Large Demand Systems.” Journal of Business & Economic Statistics, 22(2): 194-205.

Wales, Terence J., and Alan Donald Woodland. 1983. “Estimation of Consumer Demand Systems with Binding Non-negativity Constraints.” Journal of Econometrics, 21(3): 263-85.

Whitehead, John C., Daniel J. Phaneuf, Christopher F. Dumas, Jim Herstine, Jeffery Hill, and Bob Buerger. 2010. “Convergent Validity of Revealed and Stated Recreation Behavior with Quality Change: A Comparison of Multiple and Single Site Demands.” Environmental and Resource Economics, 45(1): 91-112.

Witt, Stephen F., and Christine A. Witt. 1995. “Forecasting Tourism Demand: A Review of Empirical Research.” International Journal of Forecasting, 11(3): 447-75.

Table 1. Summary of Individual Attributes (N = 1,111)

Individual attribute	Mean	SD
Gender (male=0)	0.09	0.28
Age	42.02	9.09
Annual income ($)	67147.09	36478.74
Work hours	41.00	12.08
Boat ownership (boat=1)	0.78	0.41

Table 2. Summary of Selected Sites Attributes (N = 1,111)

	Cocodrie	EL	GI	Leeville	Port Fourchon	Venice
Trips	0.86   (4.27)	2.53   (5.99)	5.84   (8.13)	0.98   (3.99)	2.22   (4.99)	0.97   (3.80)
Price	62.11   (94.91)	154.96   (124.73)	319.70   (171.05)	307.10   (159.14)	237.47   (122.95)	304.62   (160.24)
Total catch of fish per trip (TCPT)	3.87   (0.99)	3.76   (1.00)	3.68   (1.03)	3.78   (1.15)	3.74   (0.98)	4.25   (0.85)
Ease of access to site (EAS)	4.20   (0.87)	4.37   (0.91)	4.15   (1.08)	4.14   (1.08)	4.39   (0.95)	4.14   (0.85)
Low human congestion (LHC)	4.10   (0.89)	3.78   (0.95)	3.81   (1.03)	3.78   (1.01)	3.78   (0.92)	3.98   (1.01)
Level of pollution (LOP)	4.73   (0.82)	4.56   (0.95)	4.53   (1.05)	4.60   (1.03)	4.69   (0.73)	4.72   (0.65)
Abundant wildlife (AW)	3.92   (1.19)	3.89   (1.06)	3.99   (1.05)	3.93   (1.10)	3.95   (1.03)	4.22   (0.95)
Camping facility (CF)	1.85   (1.13)	2.09   (1.19)	2.23   (1.32)	1.91   (1.15)	2.02   (1.13)	1.69   (1.00)
Interpretive signs (IS)	2.00   (0.91)	2.05   (1.11)	2.20   (1.18)	1.87   (0.97)	2.10   (1.06)	1.80   (1.03)
Level of development (LD)	3.35   (1.18)	3.50   (1.38)	3.44   (1.28)	3.09   (1.24)	3.39   (1.26)	3.42   (1.02)
Rules and regulations (RR)	3.98   (1.04)	3.96   (1.23)	4.01   (1.15)	4.21   (0.99)	4.06   (1.11)	4.22   (0.96)
Nearby food and lodging (NFL)	3.56   (1.19)	2.93   (1.32)	3.28   (1.29)	3.39   (1.23)	3.24   (1.26)	3.38   (1.32)
Note: Standard deviations are reported in parentheses

Table 3. Estimation Results of KT Model (N = 1,111)

Parameter	Estimate	Standard Error	t-statistics
Ψj   index parameters
Constant	-0.91	0.99	-0.92
Age (AGE)	-0.01**	0.01	-2.42
Hours (HOURS)	-0.01**	0.00	-2.26
Boat (BOAT)	0.07	0.11	0.61
Gender	-0.30*	0.18	-1.69
Translating parameter
θ	20.39***	3.28	6.22
Repackaging parameters
Total catch of fish per trip (TCPT)	-7.28***	0.41	-17.83
Ease access to site (EAS)	6.87***	0.61	11.18
Low human congestion (LHC)	0.72	0.50	1.56
Level of pollution (LOP)	-11.16***	0.92	-12.18
Abundant wildlife (AW)	16.72***	0.83	20.17
Rho parameter
ρ	-0.61***	0.16	-3.76
Type I extreme value scale parameter
μ	0.49***	0.04	11.66
Max. Log Likelihood	-11446.86
Note: *, **, and *** donate significance difference from zero at 10%, 5%, and 1% levels, respectively. Robust standard errors and t-statistics reported.

Table 4. Welfare Estimates

Policy scenario	Welfare Estimate
Scenario 1: Closure of Elmer’s Island	-1611.07   (14.97)
Scenario 2: Closure of Grand Isle	-526.27   (15.17)
Scenario 3: Closure of Port Fourchon	-453.85   (6.96)
Scenario 4: Decrease in travel cost by $20	299.06   (5.18）
Scenario 5: Access fee at Grand Isle increased to $10	-57.19   (0.01)
Note: Robust standard errors based on 200 Krinsky and Robb (1986) simulations are reported in parentheses.

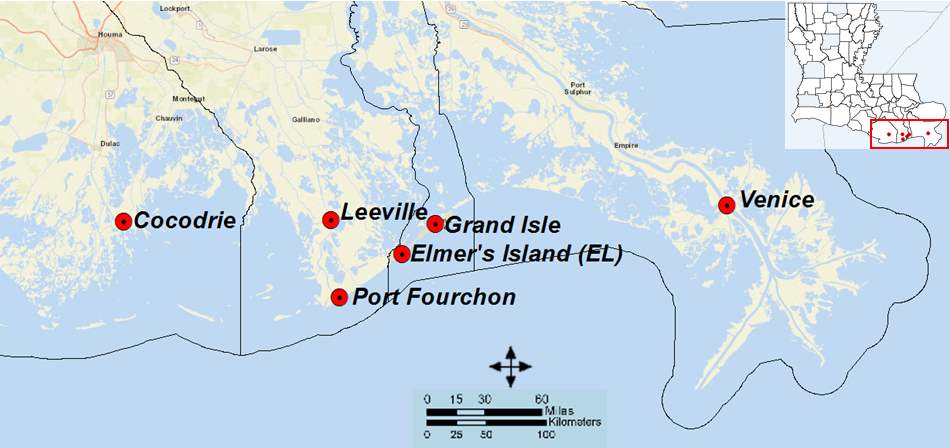
Figure 1. Study Area in Coastal Louisiana (Louisiana map is shown in the inset at the upper right corner)

---

[1] A recent study published in Science by Bishop et al. (2017) supports $17.2 billion in protection for future oil spill such as the 2010 BP oil spill that happened in the study area. The authors used a stated preference method (CV) to come up with this value. Reference: Bishop, Richard C., Kevin J. Boyle, Richard T. Carson, David Chapman, W. Michael Hanemann, Barbara Kanninen, Raymond J. Kopp et al. 2017. “Putting a value on injuries to natural assets: The BP oil spill.” Science. 356(6335): 253-254.

[2] Annual average Consumer Price Index (CPI) for all urban consumers was used to adjust these numbers to 2016 dollars.