Discrete Multitone (DMT) in Digital Subscriber Line (DSL) Communications

Thesis Abstract

Against the increasing global transmission traffic and the exponentially growing demand for high-speed data rate services in broadband digital subscriber line (DSL) communication systems, it is a deeply necessary to further research for flexible, versatility, robust and bandwidth-efficient transmission techniques. Up to now, multi-carrier modulation based multiplexing techniques play an important role for the future generation broadband communication systems. To that fact, a number of various kind of synchronous discrete multitone (DMT) transceivers are being examined in order to efficiently utilise the available bandwidth of the DSL in accordance with the traffic demand. On the one hand, these DMT transceivers are able to accommodate multidirectional transmission and have revolutionarily change the data rate and transmit power performance of copper technologies in a more meaningful ways. On the other hand, at high frequencies, DMT often suffers from poor stopband attenuations that usually gives rise to crosstalk impairments, highlighting that perfect synchronization is required. Enabling perfect synchronization makes DMT performance more feasible. Hence, introducing flexibility in the system remains one of the main goals of this study. Furthermore, minimizing the computational complexities and enhancing the spectral efficiency of the system are two critical challenge to be considered in the analysis and designs.

The research focuses on the use of filtered DMT (FDMT) based technology that can achieve a superior data rate transmission over DSL lines. Different cost-effective solutions for channel equalization are to be investigated.

On the one hand, unequally-sampled based networked systems would be investigated to tackle with present and future traffic demand. After an introduction to the principles of precoding and equalization block transmission and its application to DSL systems, the main problems of such transmission will be analysed. In particular, crosstalk is being presented as the major limitation in DMT systems, as well as peak-to-average power ratio (PAPR) and quantization noise. Hence, error mitigation techniques would be introduced to counteract these impairments. Additionally, low complexity mitigation techniques based on the channel diagonalization are also being the core algorithm to be applied with a simplified polynomial singular value decomposition (PSVD).

On the other hand, sub-problem equalization schemes are to be used in analysing the system to estimate the best performance of the DMT and to optimise the error in each transmission line independently. Moreover, thanks to per-tone power constraint, flexible and adaptive feedback equalization can be implemented to maximize the spectral efficiency by further minimise the transmission error. Finally, DMT symbols are to be mapped into different subcarriers with different modulation formats in accordance with the channel profile. Experimental validation of the proposed adaptive DMT transceivers is also to be provided in this study. The benefits of including per-tone power constraints for error minimization, such as enabling high data rate and dynamic spectrum management, are to be highlighted.

INTRODUCTION

Over the recent years, fixed wireline systems, particularly digital subscriber line (DSL) technologies, have become one of the leading methods to provide broadband communication services to end users. The emerging evolution of high-speed broadband transmissions over copper wires has led to rapid upgrading from traditional dial-up instrument to the ever-growing internet architectures. These impressive developments are presently enjoying solid market’s support all over the developed world, including in the United Kingdom, Japan, United States of America (USA) and others.

The success of DSL networks relies only on the use of existing plain old telephone service (POTS) architectures to transmit low cost services but also has been driven by the growing broadband demand for internet TV, video-on-demand services, low competitive pricing strategies as against to the wireless networked systems and other reasonably high-speed data-rate transmission services.

High-speed transmission revolution is too far from over! Research on new and versatility designs for broadband services is still promising and insatiable. In this regards, the future DSL requires an improved and a robust signal processing technique, particularly as the designs complexities increase with a number of users. The next generation marketplace is likely to become more intractable as other akin broadband services such as internet of everything (IOE) and other promising high-speed services are available over a range of communications.

The development of new advancement for DSL remains a feasible solution in other to continuingly utilise the existing technology despite the rapid advances in wireless systems. Despite being offered lower speed and reliability, wireless broadband technologies still convey far less traffic than DSL systems. As a result of this, wireless is being classically used in the rural community to compensate the demand for fixed systems. Conventionally, wireless networks are significantly impressive to transmit broadband services over the air for a short distance and switch-over to either fiber or DSL lines for longer transmissions.

The recent discovery of long-term evolution (LTE) and other enhancement technology for offloading wireless problems has further placed more challenges. Moreover, the design and implementation of a robust approach to enhance DSL systems for optimal performance have been a great challenge.

One of the techniques to cater for these issues far remains a multicarrier multiplexing (MCM) modulation. MCM is a technique that divides the available bandwidth of networked systems into several subcarriers and is being considered as future generation technology for multiple-input multiple-output (MIMO) networks since it provides high throughput, low latency, smooth granularity and efficient bandwidth utilization.

Implementing MCMs that employs a minimally splitting of a multicarrier networked bandwidth to efficiently enhance the performance of the networks and adequately overcoming the anticipated ‘impairment caused by the fast increasing capacity demand still remain uncertain. Discrete multitone (DMT) had been deployed as an MCM scheme to allocate available spectrum for various DSL networks. The conventional DMT transceivers decompose the available frequencies/bandwidth into separate channels spaced sub-data as specified by the recognised standards. This static infrastructure lead to an inefficient use of the available resources of the network when the transmitted traffic requires only part of the whole allocated spectrum. Hence, in order to improve this mismatch of granularities between the user and the frequency, cyclic prefixed DMT has been updated to support finer frequency grids enabling flexible DMT.

Specifically, in order to evolve to a more scalable and flexible grid to efficiently allocate the bandwidth resources for a very high-speed frequency selective channel as occurred in the newest VDSL-2 technology, an improved spatial multiplexing modulation are defined (further reducing the complexities minimally).

The need for spatial multiplexing and the evolution of VDSL-2 systems towards elastic functionalities and bit-rate performance from 10 Gb/s to 100 Gb/s and beyond arises new technical challenges.

Single-carrier modulation formats require high symbol rates to enable 100 Gb/s transmission and beyond, that are not technologically feasible in the near future.

Hence, advanced modulation formats, such as vectored DSL techniques, are more suitable solutions to fully exploit flexibility at the data coordination level of DSL access multiplexing (DSLAM). By using spatial multiplexing formats, efficient spectral allocation with high data rate can be achieved while minimizing complexity, power consumption and transceiver cost.

In particular, the spectral allocation can be enhanced by using second order modulation formats and smoothing technique at the expense of the receiver sensitivity and system complexity, respectively.

Additionally, the linear transmit power can be designed to fully exploit the flexibility in the data coordination level. Flexibility can further be enhanced by modelling the network in a single dynamic fashion and decomposing it into several linear transceivers known as scalable subcarrier transceivers.

On the one hand, these subcarrier modulations enable high spectral efficiency by using a spectral pulse shaping filter at the transmitter side to allow a narrow subcarrier spacing within the Nyquist frequency limit.

Thus, a dense allocation of spatial subcarriers is allowed creating an optimal preconditioning at the transmitter. However, significant power penalties arise when the channel frequency spacing is equal to the symbol rate. As a result, the convolutive model is required to enhance system performance, existing a trade-off between spectral efficiency and inter-carrier Interference (ICI). This transmission scheme becomes an interesting solution for long-haul and ultra-long-haul applications.

Although the concept of the filtered DMT modulation was first commercialised by John Cioffi in 1966, it was earlier being mention by 1996  and later applied by Pan and Green to optical communications field. FDMT achieves higher spectral efficiency when a subcarrier number of equally spaced are used. Despite its poor in unequally spaced data, this FDMT is arising as one of the most promising technology for designing bit rate and has been regarded as key enablers for future DSL due to its unique data rate/bandwidth scalability and subcarrier granularity. Additionally, FDMT also permits dynamic spectral allocation and management, which allows adaptive allocation of network resources by reconfiguring the transmitter and receiver of a DSL communication system on demand.

DMT with filter band structure is possible thanks to the advances in Digital Signal Processing (DSP) technology. Advanced vectored level modulation formats are supported by DSLAM technology providing higher data rate and spectral efficiency. Hence, FDMT becomes a promising technology to consider in the design of the linear filter design in VDSL-2.

However, high data rate transmission over unequally-spaced DSL network is affected by crosstalk impairments such as the far-near crosstalk and the bandwidth limitation of some electrical components, such as the electromagnetic interference between the bundle cables. Additionally, crosstalk impairment presents limited spectral resolution which leads to quantization noise. A major performance limiting factor of DMT systems is the far-end crosstalk of the transmitted signals, which can result in a rapid signal degradation. A symbol transformation scheme needs to be adaptively adjusted in order to accommodate the victim DMT signal. Specifically, a reliable synchronization occurs when multiple DSLAM subcarriers that interfere constructively can be superposed. Therefore, the DSLAM must ensure a dynamic range up to the value of the finite difference of the signal arrival. A possible way to adjust the dynamic range of the DSLAM to a lower value is by the use of higher frequencies to transmit the symbols. Widening the bandwidth results in enhancing the effect of the impairment at the receiver, which also further degrades the system performance. Due to all these impairments, hardware limitations and high implementation costs, frequency widening DMT technology cannot be considered as a near-term solution for VDSL-2.

Depending on the application, different dynamic crosstalk mitigation schemes are being used to allow high-speed data rate transmission, compromising between the cost-effectiveness and performance. Specifically, optimal performance can be achieved using the correlation of the square error at the receiver, where the system robustness against transmission error is imposed at the expense of increasing the system cost.

Alternatively, minimum mean square error (MMSE) estimation that uses a simple transmitter and receiver architectures appear promising as a potential cost-effective candidate to reduce the cost and complexity of the FDMT implementation.

In a typical implementation, a single precoder and a single equaliser are needed in transmission and reception, respectively, for a single-user transmission. The simple single-user signal processing of the DMT transmitter/receiver is centrally based on the polynomial model. Nevertheless, the polynomial representation an alternative transform to the fast Fourier transform (FFT) that can also be used to implement the dynamic symbols, further simplifying the complexity of the system.

Different decomposition technique can be adopted to extract true transmission symbols. However, one of them, the broadband singular value decomposition (BSVD) has attracted attention for the application in beamforming and channel coding. Recently, BSVD has been proposed as a low-cost approach for DSL transmission of up to 100 Gb/s data using redundant filter bank components.

Crosstalk resilience in PSVD can be enhanced by using linear transmit filters that allow only single-side band (SSB) instead of double-side band (DSB) transmission. In this thesis, cost-efficient adaptive solutions using BSVD algorithms are proposed in order to build novel dynamic spectrum management architectures to meet the requirements of future DSL systems. The goal is to limit the aforementioned system impairments and enhance the system performance using low complexity BSVD in order to drive the use of DMT technology in VDSL-2. Crosstalk mitigation techniques are analysed to optimise the crosstalk impairment at the receiver using the cross correlated technique with decision feedback estimation scheme. On the other hand, spectral efficiency and adaptive features are provided by implementing loading algorithms in the single-user bases. Moreover, per-user equalization schemes are also suitable to deal with crosstalk impairment. These solutions can be found application in dynamic spectrum-level coordination and signal-level coordination using flexible technology, as possible target applications. In particular, PSVD based FDMT systems are investigated for DSL systems. Whereas, DMT systems are analysed in order to allow dynamic high data rate transmission over the existing POTS connections.

Background and State of the Art

Very High-Speed DSL Transmission

Current DSL (VDSL2) networks require an advancement in order to support very high-speed transmission and must be low cost to compete with other broadband communication networks. These networks utilise the traditional plain old telephone service to transmit over copper twisted pair wires.

Copper susceptibility to interference becomes a major factor limiting the performance. This limiting factor often wraps around the transmitted data and can cause a significant impact on the link reliability, the throughput of the services and the coverage performance.

Electromagnetic interference (EMI) and crosstalk impairment are two common sources of interference within a copper environment. EMI occurs when electrical signals from the local environment outside of the binder are picked up by the copper pairs in a cable and introduce noise.  Whilst, crosstalk impairments occurs when a signal transmitted on one copper twisted pair in a bundle radiates and potentially interferes with or degrades the transmission on another pair.

These bottleneck limitations become more severe at the increasing of the data rate.

Hence, looking for an advanced technology that can effectively mitigate these kinds of interferences can enable carriers and that also supports high data rate transmission at the coordination levels become a trending topic to enable next generation DSL networks. In fact, managing crosstalk dynamically can significantly enhance the reliability of the link and the performance of the services and makes copper suitable for longer transmission distances to enable service operators to reach more customers.

Broadband transmission over copper technologies requires sophisticated modulations and techniques that can effectively identify and mitigate crosstalk.  These modulation makes transmission over copper carrier class, dramatically increasing the signal to noise ratio (SNR), reliability, network quality of service (QoS) and overall throughput performance.   Although discrete multitone (DMT) modulations are standards-based techniques required to eliminate noise and ensure high performance transmission over short/long range copper wires.

As a high number of links are required for transmission, data connection centre must evolve to further increase the channel capacity and accommodate every link interface. In fact, DSL access multiplexing (DSLAM) technology is already standardized for VDSL-2 and vectored bonding solutions for the physical layer are under investigation in order to support the future incoming demand.

The need for improving the spectral efficiency combined with the newly built DSLAM centres and the influence from providers make really difficult to predict the efficient signalling structure.

Many combined data-links must design as point-to-point networked interfaces, each link is to be transmitted independently. Hence, a DSLAM usually occurs at a telephone company central office (CO) or local terminal (LT) near the user and receives signals from multiple customer connections and puts the signals on a high-speed backbone line with multiplexing procedures.

Common applications of DSLAM can be general spectrum level and signal-level coordination which typically involve the major network resources control. As a high number of links are required to interconnect all the data links over an area, simple and low-cost DSLAM solutions need to be investigated. However, maintaining low cost and high spectral efficiency when a large number of communication links is transmitted still remain uncertain. The network signalling condition and achievable data rate are to be dynamically structured by implementing robust and adaptive networks equipped with flexible DMT Transceiver, which are key enablers of VDSL-2.

In [], VDSL-2 transmission is demonstrated using two sided DMT modulation that is a special class of Orthogonal Frequency Division Multiplexing (OFDM) systems.  Specifically, better performance data rate than asymmetric DSL is achieved after 5 km, ensuring a target Bit Error Rate (BER) of 10−3, which can satisfy the short distance connection between DSLAM centers.

Hence, filtered DMT (F-DMT) also arises as a potential solution for high data rate transmission in short-links scenarios. Additionally, this equipment and its integration can be a future possible solution to reduce the system cost and physical layer metrics performance.  Recently, filter bank- based DMT transceiver are promising technologies under investigation that achieve high power reduction and energy efficiency.

Filtered DMT Networks

Filtered DMT F-DMT arises as a potential solution to deal with high data rates (beyond 100 Gb/s). However, upgrading the current DSL network towards dynamic functionalities usually requires an additional effort. In particular, the deployment of new network infrastructures and the increasing of the electrical power consumption involves high capital expenditure and operational expenditure, respectively. Hence, the spectral and energy efficiency, the flexibility and the network equipment costs will be crucial parameters to take into account when designing the future communication links.

Highly efficient and adaptive management of the power spectral can be achieved by using a correlated mean square error (MSE) technology. Specifically, finite differences spacing is considered, for the unequally spaced-data, to adaptively optimise variable-sized frequency slots to bandwidth-variable copper connections, according to the each user data rate and the physical conditions of its path.

Additionally, the use of an advanced polynomial model that can efficiently use allocated spectrum slots, fully exploit the parallelism and enabling dynamic spectrum management (DSM) in the VDSL-2 environment. In fact, a polynomial model with MSE is considered as DSM technology enablers for high data rate transmission, which can multiplex and switch variable spectral bands. Hence, the flexibility and scalability of the network are maximized and the cost and energy consumption minimized.

A possible use case of DSM using channel decomposition algorithms has been investigated in the literature. Typically, DSM architectures are composed of two main levels of aggregation. The first level of aggregation, called spectrum-level coordination, is in charge of collecting data from the DSL Line Terminal. Whereas, the second level of aggregation is the signal- level coordination, which aggregates the traffic from the each user mainly through direct DSM connections.

In fact, as cost effectiveness is an important requirement for the system design, it is desirable to adopt low complex data plane solutions to further minimize the network cost. Additionally, local optimization technique can benefit from the use of polynomial model and channel diagonalization technique at the coordination center, enhancing system’s flexibility.

Discrete multitone Multiplexing

DMT is a special class of multicarrier modulation (MCM) technology that can transmit a signal over several lower-rate orthogonal subcarriers. The bandwidth of each subcarrier, which has a sin(x)/x form, can overlap due to its orthogonality.

As it has been shown in [] that the different subcarriers that form the DMT symbol are a low-pass filter, and each subcarrier has significant sidelobes over a frequency range.

On the one hand, DMT presents robustness against channel dispersion and allows an easy phase and channel equalization in a time-varying environment.

Thanks to the use of a Cyclic Prefix (CP), the channel dispersion-caused intersymbol Interference (ISI) and intercarrier Interference (ICI) can be resolved.

The CP is a cyclic redundancy introduced in the DMT symbol. The elements in the tail of the discrete DMT signal vector are reproduced as a prefix.

On the other hand, DMT suffers from crosstalk interference and other related impairment like the high Peak-to-Average Power Ratio (PAPR) and sensitivity to frequency offset and phase noise.

The crosstalk mitigation problem will be detailed and analyzed in this study.

Whereas frequency offset and phase noise appear due to the relatively long symbol length and they lead to ICI. Channel equalization can be implemented at the receiver side to mitigate the frequency offset sensitivity.  The phase noise sensitivity can be resolved by careful turning the Radio Frequency (RF) local oscillators.

In order to create the orthogonal subcarriers, DMT exploits the inverse fast Fourier transform (IFFT) and the fast Fourier transform (FFT) for the modulation and demodulation of a signal, respectively.

The IFFT can be defined as:

ym = 1 √ N N X−1 n=0 Yn exp(2jπmn/N) m = 0, 1, …, N − 1, (2.1)

where Yn indicates the symbol sequence, previously mapped with an M Quadrature Amplitude Modulation (MQAM) or M Phase Shift Keying (MPSK) format, and N represents the number of subcarriers.

The symbols have different energy levels when they are mapped into MQAM constellation. Whereas, with the mPSK format, they are distributed in a circle of unitary energy.

Using MQAM, for a large M, the symbols have more distance between each other and hence, the receiver can recover the signal with fewer errors.

Nevertheless, more power is needed to transmit them.

For large-size constellations, MPSK format is not suitable, due to the reduced distance between symbols.

The constellations of both modulation formats (for 16 symbols) are depicted in Fig. 2.4.

The block diagram of the transmitter is shown in Fig. 2.5 and it is composed by a Serial to Parallel (SP) converter, a mapper, a block to insert the Training Symbols (TS), an IFFT of N points, a block to insert the CP and a Parallel to Serial (PS) converter.

With the mapping, a certain number of bits is represented by each mapped symbol. The IFFT block generates an OFDM symbol with N orthogonal subcarriers. Finally, the resulting signal is serialized, digital-to-analog converted with a Digital-to-Analog Converter (DAC) and sent through the channel.

At the receiver, Fig. 2.6, the inverse process takes place.

Firstly, after the detection of the signal, the received data is analog-to-digital converted by an Analog-to-Digital Converter (ADC). The resulting digital signal is parallelized in order to remove the CP in the following step. Then, the FFT is implemented and equalization is performed. Finally, the resulting signal is demapped and serialized in order to recover the original bit stream.

DMT in DSL Communications

One of the reasons why DMT has been applied to DSL communications is its capability to use high modulation formats to increase the spectral efficiency high signal-transmission capacities according to the future and growing demand.

However, the use of high order modulation formats experiences the presence of crosstalk, resulting in a low Signal-to-Noise Ratio (SNR) tolerance.

In order to overcome this limitation, reconfigurable transceivers can be implemented to adapt the system to the current traffic demand and network condition.

In fact, Filter-bank based DMT has been proposed to cope with upgrades to the next transmission speed in highly reconfigurable networks.

It is also a good option for DSL with long-haul communications especially because it can be used to be extremely tolerant to approximate linear transmit power. Additionally, FB-DMT is a key enabler of future VDSL-2 as it can be combined with bit loading and power loading.

Channel identification and equalization are two possible mitigation techniques for receiving the optimal transmitted signal through a distorted channel. On the one hand, channel equalization (CE) through correlated mean square error (MSE) estimation is a very attractive design implementation due to its low cost and it is suitable for DSL. In such designs, the estimation is evaluated using a single-user approximation technique. Additionally, the CE problem can be formulated with a single –user constraints by preconditioning the signal at the transmitter.

Optimal channel equalization is explained in more detail in section 2.4.1, as it is the solution adopted in this thesis.

On the other hand, a precoding-equalisation technique is an alternative high data rate implementation which was proposed to combat crosstalk impairment in long haul transmission.

It presents better performance than channel equalization with single feedback detection estimate.

DMT in terms of bandwidth efficiency, robustness against dispersion and receiver sensitivity, but it requires higher complexity in the transceiver design than existing DSL systems.

Hence, single-user detection scheme results in a more cost-effective solution. According to [], reduced power consumption can be achieved in either optimal equalization or coherent correlation when moving towards linear transmit filter designs. However, single-user equalization systems require additional computation analysis, whose data rate performance is so much more demanding than in existing systems.

A typical precoding and equalization block diagram is depicted in Fig. 2.7. The DMT in phase and quadrature components of the complex-valued signal is modulated by using a filter bank precoding scheme at the transmitter. Then the modulated signal is transmitted over the DSL channel. In reception, one laser as local oscillator, balanced and per-user channel equalization are needed to recover the transmitted signal. Finally, both components are filtered and demodulated at the equalisation end.

Per-User equalization

Per-user equalization has been presented as a low cost and low complexity signal configuration and becomes a suitable solution to meet the requirements of this thesis. This single user transmission designs and its analysis can be exploited in a broader range of applications due to its transmitter (precoder) and receiver (equalizer) simplicity. Per-user variants can be estimated depending on the sampling rate factors.

On the receiver side, a simple single detector each for a user is only needed to directly detect the signal.

The single-user detector has lower responsivity and cost than a multi-user detector. Despite that, the common feature in all possible per-user detector schemes is the use of individual detection at the receiver, alternatives to generate the transmitted signal exist.

Regardless of the implemented transmission architecture, the different estimator can be used to perform the point-to-point single-user transmission.

Specifically, zero-forcing (ZF) estimator, and mean square error (MMSE) estimator directly modulate the time-domain signal into the frequency domain.

ZFs provide high output power and the low threshold above some certain constraints. However, it performs poorly when the transmission problem is unstructured or unequally spaced data.

Alternatively, the real DMT signal can be externally estimated in the MMSE context.

The MMSE is limited to the filter length. In contrast, ZF is a typically used for the ICI-free system as it assumes that the transmission is negligible free from interference.

Hence, MMSE provides more design freedom and can achieve better performance than ZF at the expense of increased cost.  The MMSE equalisation allows a double-side band (DSB) spectrum with respect to the available frequency cutoff.

It is shown in [] that DSB transmission is very susceptible to dispersion problem, however, it is simple to implement using a spatial-temporal analysis.

Alternatively, the single-side band (SSB) was proposed by Schmidt et al. in [] for frequency selective channel in wireless systems.  SSB modulation ensures that the subcarriers signal with its power spectral can be represented only once by the finite frequencies differences, and thus avoid interference.  SSB modulation consists of suppressing one of the two DMT sidebands that represent the real signal.  For this purpose, linear transmit filters designs or more complex schemes are required.

Furthermore, the introduction of the guard band, in cyclic prefix DMT modulation, which equal to the length of the transmitting signal must be considered, reducing the spectral efficiency.

Moreover, designing of linear transmit filter solely depend on the sampling rate factors. Thus, the unequally-spaced data problem in multicarrier systems can also be contained.

Unequally-spaced modulation is achieved by regularising the MMSE at the quadrature point. Additionally, regularised MMSE can also be implemented through an effective channel diagonalization.

Filter bank DMT with USM: MMSE-biased solutions

When the sampling rate is non-uniform, the system is less robust against dispersion impairments due to the nonlinear mapping between the DMT baseband signal and the copper field. In USM systems, using direct laser modulation, the DMT signal is represented by its finite differences. Thus, the transmitted signal must be unipolar.

A true signal can be obtained by applying channel diagonalization to the real DMT signal generated by a DMT transmitter.

Channel Diagonalization

Channel diagonalization consists of modulating only the odd subcarriers and set to zero the even ones.

Then the signal can be clipped at zero level without any lost of information.

The odd frequencies have the property that: Yn = −Yn+N/2, (2.2)

where N is the number of subcarriers and Y is the input vector of the real-valued FFT block.

Thus, the useful information in the odd frequencies is redundant and we can cut at zero level without any loss of performance.

The clipping noise falls in the even subcarriers, which can be discarded at the receiver side.

With this scheme, the optical power is substantially reduced, but in contrast, it only carries useful information on half of the available signal bandwidth.

DCO-OFDM DCO-OFDM consists of adding a bias (B) to the signal and then clipping it at zero level.

The resulting signal from this asymmetrically clipping can be written as: yˆm =    0, ym + B ≤ 0 ym + B, ym + B > 0 (2.3)

Alternatively, symmetrically clipping can also be applied.

It consists of limiting the amplitude of the signal and then adding a bias equal to this maximum amplitude value in order to ensure a positive signal.

The symmetrically clipped digital OFDM signal can be represented by yˆm =    ym, |ym| ≤ B B · sign(ym), |ym| > B (2.4)

where B is also the maximum allowed signal amplitude and it is k times the standard deviation of the signal.

The clipping level (C) is defined in decibels as C = 10 · log10  B2 E[|ym| 2 ], (2.5) where E[|ym| 2 ] denotes the average signal power of the transmitted signal.

Symmetrically clipping is also used to limit the high PAPR of O-OFDM signals.

However, clipping the signal introduces a penalty due to the appearance of clipping noise that degrades the performance of the system.

Usually, the value of the clipping level is 7 dB [47]. However, when high order modulation formats are used, 7 dB clipping level is not enough to guarantee a BER lower than 10−3.

Higher clipping level values can be applied to the signal for reducing the clipping noise at the expense of increasing the electrical power of the signal [21, 47].

Hence, there is a trade off between power efficiency and noise in the selection of the clipping level or bias.

ACO-OFDM and DCO-OFDM comparison Fig. 2.10(a) shows an OFDM frame with only the odd subcarriers modulated (ACO-OFDM).

Therefore, as the signal has odd symmetry according to equation (2.2), we can clip the signal without loosing data, as it can be seen in Fig. 2.10(b).

In Fig. 2.10(c) it is represented one OFDM frame with all the subcarriers modulated and Fig. 2.10(d) shows the signal clipped to the zero level after adding a bias of twice the standard deviation of the original signal (DCO-OFDM).

DCO-OFDM allows transmitting more information than ACO-OFDM with the same bandwidth, implying higher spectral efficiency.

However, clipping noise could degrade the transmission.

ACO-OFDM can be easily used in adaptive systems using different modulation formats to transmit the OFDM symbols as an optimum performance with the same design can be achieved [48].

Whereas with DCO-OFDM, the bias must be constantly adjusted depending on the constellation size.

Alternatively, the bias can also be fixed according to the highest modulation format at the expense of reduced power efficiency.

Real-valued OFDM symbol generation As it can be seen in Fig. 2.8 (a), (b), (c) and (d), different transmission architectures can be implemented to create a real OFDM signal.

Specifically, a first solution is based on an RF modulation of the OFDM baseband signal, as shown in Fig. 2.8(a).

Once the OFDM symbol is digitally generated, the real and imaginary part is converted to the analog domain separately.

The next step is to modulate the signal to RF, multiplying the real part by a cosine and the imaginary part by a sine and then adding both signals obtaining a real signal.

An oscillator at an intermediate RF frequency, fi, is required in order to implement the modulation [25]. A second DD scheme is shown in Fig. 2.8(d) and it uses the properties of the Hilbert transform to create an SSB signal without using an optical filter.

Modulating the real and imaginary parts of an analytic signal, an optical signal with no-negative frequency components is obtained.

In order to have an analytic signal at the output of the IFFT, half of the elements of the input vector must be set to zero.

Discrete Multitone Modulation An alternative scheme to create real OFDM signals with simplified implementation is DMT modulation (see Fig. 2.8(b)).

The Hermitian Symmetry (HS) is forced at the input symbols of the IFFT in order to have a real valued signal at the output of the transform [47].

The principle of DMT is depicted in Fig. 2.11. The mapped symbols are divided into N subcarriers. The first half, from input 1 to input N/2 − 1 of the IFFT, carry useful data.

Whereas the first and the N/2 inputs, the Nyquist frequencies, are set to zero.

Then, according to the HS property, the second half of the available inputs carry the flipped complex conjugate version of the first half.

As a result, real data is obtained at the output of the IFFT. YN−n = Y ∗ n n = 1, …, N/2 − 1. (2.6) Principle of FHT-based O-OFDM in DD systems

Finally, the last analyzed option is depicted in Fig. 2.8(c) and it is based on the implementation of the Fast Hartley Transform (FHT) [21].

The FHT is a real trigonometric transform that can be used in OFDM [49, 50] and O-OFDM [21] as an alternative transform to the FFT.

It gives real data when the input signal is mapped into a real constellation, such as

0 Y1 N/2 N/2+1 N-1

Complex conjugate N-IFFT 1 YN/2-1 N/2-1 Y * N/2-1 0 0 Y * 1 Y2 Y * 2 Real data Real data Real data Figure 2.11: Schematic of DMT modulation.

Binary Phase-Shift Keying (BPSK) or M-ary Pulse Amplitude Modulation (MPAM), where M is the constellation size.

The FHT allows simplifying the Digital Signal Processing (DSP), as it has the same routine in transmission and reception and does not require to implement the HS.

The transmitted discrete signal, xm can be written as, xm = 1 √ N N X−1 n=0 Xncas(2πmn/N) 0 ≤ m ≤ N − 1, (2.7) where cas(2πmn/N) = cos(2πmn/N) + sin(2πmn/N), N is the number of subcarriers of the FHT and Xn is the n−th element of the input vector X = [X0 X1 X2 … XN−1] T .

Since, no symmetry constraint is required, all the subcarriers are filled with data, whereas, when the FFT is used, only half of the subcarriers carry information [47].

Both transforms have similar complexity and the same performance in terms of spectral efficiency and BER [21, 51].

The transform kernels of the FFT and the FHT only differ for the imaginary unit, as the real and imaginary parts of the FFT coincide with the even and the negative odd parts of the FHT, respectively. Due to the kernel structure, the mirror-symmetric sub-bands of the FHT ensure subcarriers orthogonality, resulting in a suitable basis for OFDM modulation.

The same spectral efficiency and bit optical power are obtained using the FHT with BPSK, 4PAM and 8PAM formats or either using the FFT with 4QAM, 16QAM and 64QAM formats, respectively, as demonstrated in [52]. A typical DD scheme based on the FHT uses an MZM [51, 53].

Chromatic dispersion in SSMF

Chromatic dispersion is one of the major limitations in transmission over optical fibers [9, 54, 55]. At the increasing of the fiber link length, other impairments such as fiber nonlinearities also appear.

CD occurs because of short optical pulses enters in the fiber spreading out into a broader temporal distribution which causes signal distortion.

Specifically, different spectral components of the pulse travel at slightly different group velocities causing CD.

The CD can be expressed as the sum of two contributing factors: the material dispersion and the waveguide dispersion.

The dispersion parameter D is defined as D = − 2πc λ 2 β2, (2.8) where c is the light speed, λ is the center wavelength and β2 represents the dispersion of the group velocity and it is the responsible for pulse broadening.

At the increasing of the fiber length (L), CD impact is higher. As a result, various subcarriers are highly attenuated. Specifically, the power penalty in decibels introduced by the CD is defined, according to [9, 20, 56] as P enalty = 10log 1 cos( πLDλ2(fCD) 2 c ), (2.9) where fCD is the frequency of the subcarrier. According to [20] and equation (2.9), the n-th attenuation peak due to CD (being n any positive integer), appears at the frequency f n CD = r c(2n − 1)/2λ 2 LD. (2.10)

Cross Talk is one of the main limiting factors that impact the performance of the existing copper cable plant. Managing crosstalk effectively and dynamically can significantly enhance the reliability of the link and the performance of the services riding over it, and makes copper suitable for longer transmission distances to enable service operators to reach more customers.

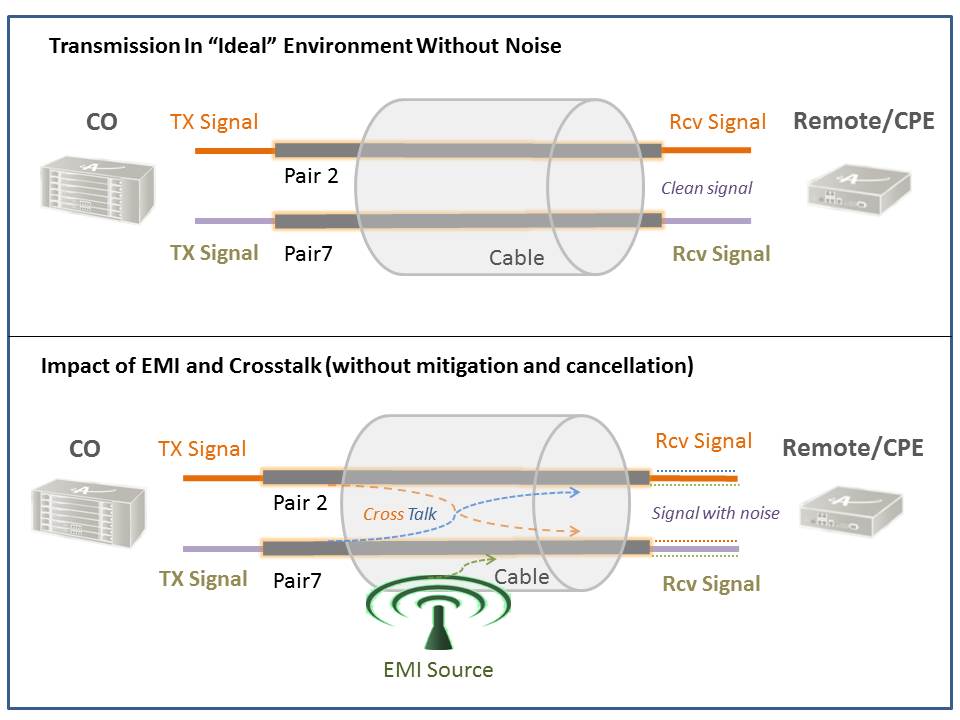
Crosstalk occurs when a signal transmitted on one copper twisted pair in a bundle radiates and potentially interferes with and degrades the transmission on another pair.  Left unchecked, this can reduce the signal to noise ratio (SNR), and historically was a limiting factor to transmission over copper binder

Crosstalk can and will typically happen between pairs/services within the same copper cable or binder.  Cross talk is strongest within the same binder and depends on the placement and proximity of pairs.  It can also be strong between binders – but tends to be negligible between cables.

Most cross talk is generated at both ends of the link, i.e. at the CO and at the CPE/NTU side.  The amount of Crosstalk generated is inversely proportional to the distance between the pairs within the binder/cable.

What kinds of noise could potentially impact a G.SHDSL transmitted signal?  Electromagnetic Interference (EMI), Near End Crosstalk (NEXT), and Far End Crosstalk (FEXT). G.SHDSL bonded copper solutions are potentially be impacted most by NEXT if it is not overcome.  DMT bonded copper (VDSL2 bonded copper) is potentially impacted most by FEXT, so overcoming this is most important to ensuring top performance.

External Noise:   External Noise can be for example – thermal, EMI, AC radiation, radio signals, motors, fluorescent lights, rectifiers, etc. that can create performance degradation of the signal

NEXT (Near End Crosstalk):  Next is generated by disturbing signals emanating from other transmitters at the same end of the loop, near the victim receiver. Next, is measured at the same end from which the disturbing signal is transmitted. NEXT can highly impact G.SHDSL based technologies.

FEXT  (Far End Cross Talk); FEXT is generated by disturbing transmitters at the opposite end of the loop, FAR from the victim receiver. FEXT is measured at the other end of the cable furthest from the transmitter. FEXT can highly impact DMT, i.e.  VDSL2/ADSL2+/ADSL2/ADSL based technologies.

Channel Estimation and Equalization

Channel estimation is a key process to correctly recover the transmitted data at the receiver side. Different approaches have been presented in the literature to perform channel estimation in OFDM systems [9], which is required for the equalization.

Some of them estimate the channel frequency response using consecutive OFDM symbols (TS), whereas in the case of time-variant channels a group of subcarriers (pilot tones) is used.

The use of CP, seen in section 2.3, combined with equalization allows a correct recovery of signals distorted by a linear dispersive channel.

This represents an overhead in the transmitted signal, which reduces the supported data rate.

The total symbol duration is given by the duration of the OFDM symbol and the additional component of the CP length.

Generally, the CP is a small fraction of the OFDM symbol, but to be effective should be longer than the delay spread.

As the FFT order increases, the impact of CP on the data rate becomes less significant.

Generally, a 10% CP is considered in practical systems.

It has been demonstrated that large dispersion tolerance is achieved using long OFDM symbol lengths [57].

Additionally, if the receiver FFT window is aligned with the start of the main symbol period of the first arriving signal and the delay spread, introduced in the system by the channel, is smaller than the CP, then no ICI or ISI occurs.

Periodically inserting training symbols imply also an additional overhead which depends on the total frame length and the number of TS.

Using a one tap equalizer, in FFT-based OFDM systems, amplitude and phase errors can be corrected at the received side by performing one complex multiplication for each element.

In order to explain the frequency domain equalization we define the IFFT matrix Q, according to [58]:

Then, the channel output can be expressed in matrix-vector form as:

s = Py + n, (2.12)

where P is the circular channel matrix and n is the additive noise added by the channel. P can be decomposed following [58] as P = QΩQ−1.

Ω is a square diagonal matrix with the eigenvalues of the matrix P on the diagonal.

Hence, from the frequency domain point of view, the diagonal of the matrix Ω can be seen as the FFT of the channel input response.

Therefore, it can be estimated using different adaptive signal processing methods with the insertion of TS or pilot tones, as described above.

The demodulated signal can be written as S = Q−1 s.

Finally, S is equalized by multiplying the received data with the inverse of Ω in order to recover the transmitted signal.

From this first step equalization, decision directed channel estimation is performed by using the equalized data as an input for a second step equalization.

Specifically, the equalization matrix is updated and it can be used to retrieve the transmitted data.

On the other hand, when the FHT is used, as each data symbol is transmitted over two mirror-symmetric subcarriers due to the kernel structure of equation (2.7), two correction factors are required for equalizing each vector element at the receiver side to retrieve the transmitted data.

However, since the FHT is a real transform and the mapped symbols are real-valued, no complex calculations are needed for the equalization processing [58, 59].

In fact, only two real-valued multiplications and one addition per vector element are required to equalize the N received data.

Furthermore, it is important to note that, thanks to the FHT symmetry property, if half of the vector elements of the training symbols are set to zero, a simplified channel estimation is possible, as only N real-valued divisions are performed to estimate all the equalization matrix factors [59].

Therefore, this low complexity FHT equalization processing has the same computational load as the equalization processing based on a real-valued FFT, which requires a half-length (N/2) equalizer.

In fact, taking into account the redundancy of the transmitted symbols in the FFT scheme, due to the HS constraint, the equalization matrix is N/2-dimensional, but complex computations (4 real multiplications and 2 additions each tap) are performed to recover the transmitted data and complex divisions are required to estimate the response of each subchannel.

Synchronization in OFDM systems

Different synchronization techniques have been proposed in the literature for OFDM systems [60–63].

In particular, Schmidl & Cox solution is presented in [60] as a robust and rapid method for synchronization in OFDM systems.

This algorithm finds an approximation of the starting point of the OFDM symbol by using a TS in which the first half is identical to the second half in the time domain.

Thanks to the use of a CP, higher tolerance is achieved in the algorithm solution search. In this thesis, a variation of this algorithm has been implemented transmitting two identical TS to estimate the beginning of the OFDM symbol.

This way, these TS can also be used to perform the equalization processing. A timing metric, M(d), as defined in [60], is calculated.

The correlation metric P(d) is given by P(d) = L X1−1 m=0 (r ∗ d+mrd+m+L1 ), (2.13) where L1 is the length of the symbol, d is a time index corresponding to the first sample in a window of 2∗L1 samples, r is the received signal and ()∗ represents the conjugation operation.

This operation is performed for all the received OFDM symbols.

The energy of the OFDM symbol, R(d), is defined as R(d) = N X−1 m=0 |rd+m+N | 2 (2.14) Chapter 2. Background and State of the Art 25 (a) (b) Figure 2.12: Timing metric before (a) and after (b) the average windowing.

Finally the timing metric can be written as M(d) = |P(d)| 2 (R(d))2 . (2.15)

The timing metric reaches a plateau with length equal to the difference between the length of the cyclic prefix and the length of the channel impulse response.

Any point included in this plateau is a valid shift approximation that gives the OFDM symbol beginning. In order to increase the accuracy of the search, an average windowing is used to create a peak at the medium point of the plateau, which is selected as the start of the symbol.

As an example, Fig. 2.12 shows the timing metric before (a) and after (b) implementing the average windowing.

Specifically, the plateau of the timing metric can be seen in Fig. 2.12(a). Whereas the estimated shift value is depicted in Fig. 2.12(b).

Considering N = 256, 20 OFDM symbols, a CP of 10% and 16QAM format, the detected shift is around the 11200 sample.

Once the symbol beginning is estimated, the received data can be shifted by this number of samples in order to recover the transmitted data.