Application of Heisenberg’s S Matrix Programme to Rainbows
Info: 12636 words (51 pages) Dissertation
Published: 17th Feb 2022
Tagged: Chemistry
Application of Heisenberg’s S Matrix Programme to rainbows, supernumerary rainbows and interference effects in the angular scattering of chemical reactions
ABSTRACT
We investigate the existence of primary rainbows, supernumerary rainbows and diffraction interference effects in the product differential cross sections (DCSs) of state-to-state chemical reactions. The rainbows can be “pronounced” or “hidden”. Our theoretical approach uses a “weak” version of Heisenberg’s scattering matrix program (wHSMP) introduced by X. Shan and J. N. L. Connor, 2011, Phys. Chem. Chem. Phys. 13 8392. This wHSMP uses four general physical principles for chemical reactions to suggest simple parametrized forms for the S matrix; it does not employ a potential energy surface. We use a realistic parametrization in which the modulus of the S matrix is the sum of a smooth-step function and a gaussian function; both are functions of the total angular momentum quantum number, J. We then vary the parameters in the modulus.The phase of the S matrix is a cubic polynomial in J, which is held fixed. We demonstrate for a Legendre partial wave series (PWS) the existence of primary rainbows and supernumerary rainbows (both pronounced and hidden) as well as diffraction interference effects, in reactive DCSs. We find that reactive rainbows can be complicated in their structure. We also analyse for five examples, the angular scattering using Nearside-Farside (NF) PWS theory, including resummations of the PWS. In addition, we apply full and NF asymptotic (semiclassical) rainbow theories to the PWS − in particular, the uniform Airy and transitional Airy approximations for the farside scattering. This lets us prove that structures in the DCSs are indeed primary rainbows, supernumerary rainbows as well as diffraction interference effects.
1. Introduction
The experimental measurement, and theoretical calculation, of differential cross sections (DCSs) for state-to-state chemical reactions is a topic of fundamental significance in atomic and molecular physics. This is because DCSs contain detailed information on the mechanism and dynamics of a reaction. However, one major difficulty is that DCSs often exhibit complicated interference structures: the interpretation of these structures is then an important and difficult task.
One powerful approach for understanding structure in DCSs is the discovery and analysis of generic dynamical phenomena. Consider, for example, the recent discovery of rainbows in the DCSs of state-to-state reactions [1-4]. Broad farside rainbows of the Airy type (fold catastrophe) have been found in the DCSs of the F + H2 → FH(vf = 3) + H reaction[1, 2] (here vf is the quantum number for the final vibrational state). A uniform asymptotic (semiclassical) analysis of the large number of interfering partial waves contributing to the scattering amplitude proved that these rainbows are a generic phenomenon. They have also been describedas “hidden” rainbows [4] because their appearance in a DCS is quite different from the familiar rainbows of elastic scattering.[5-7] Indeed, it took 24 years before it was realized [1] that the DCSs measured by Neumark et al.[8] for the F + H2 reaction contained an attractive (or farside) rainbow with unusual properties. Rainbows are also present [2] in the more recent experimental measurements of DCSs for the F + H2 reaction by Wang et al. [9]
The discovery of broad hidden rainbows in refs. 1, 2 raised the question: Can localized and pronounced rainbows occur in the DCSs of chemical reactions? E.g., are there rainbows possessing a prominent primary rainbow of the Airy type accompanied by supernumerary rainbows? A start to answering this question was made in ref. 4, where the answer was found to be “yes”.
The theoretical approach of ref. 4 employed a simple, yet powerful, procedure based on a “weak” version of Heisenberg’s scattering matrix program (wHSMP).[10-16] In particular, it employed a parametrized form for the scattering (S) matrix, which obeyed four general physical principles relevant to state-to-state chemical reactions.
The procedure we used previously to calculate DCSs varied the parameters in the phase of the S matrix, but kept its modulus fixed. This allowed us to obtain a partial understanding of rainbow phenomena in reactive DCSs. However our goal is to obtain a more comprehensive understanding. In this paper we extend and complement our earlier findings [4] by using a fixed phase for the parametrized S matrix but changing its modulus.
This paper is arranged as follows. Section 2 describes the general physical principles used in wHSMP for the design of an S matrix. Our approach can be summarized by the following scheme
initial states → S matrix → final states.
It does not employ a potential energy surface. Previously wHSMP has been used to obtain worthwhile and novel insights into structured DCSs for the H + D2 and F + H2 reactions.[14-16] In this paper, rather than consider a particular reaction, we generalize our previous work and consider a whole class of reactions as defined by their S matrix elements.
The parametrized S matrix form we use is described in section 3. The phase of the S matrix is a cubic polynomial in J, which is held fixed. Here J is the total angular momentum quantum number. The modulus of the S matrix is the sum of a realistic smooth-step function and a gaussian function, both dependent on J. We then vary the parameters in the modulus to understand better the properties of reactive DCSs.
In section 4, we summarise the theoretical techniques used in our calculations. They include Legendre partial wave series (PWS), and its first order resummation, for the scattering amplitude, as well as nearside-farside (NF) theories and the uniform Airy and transitional Airy asymptotic (semiclassical) approximations for the PWS. The use of the Airy approximations is important because it lets us prove the genericity of the rainbows, both hidden and pronounced.
Section 5 describes and discusses our results for five different examples; most results are displayed graphically. Our conclusions are in section 6.
The theory presented in this paper is for the following generic state-to-state chemical reaction:
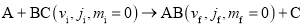
where vi, ji, mi and vf, jf, mf are vibrational, rotational and helicity quantum numbers for the initial and final states, respectively. It is assumed that the reaction occurs at a fixed total energy, or equivalently a fixed initial translational wavenumber. Note that wHSMP is also valid for reactions with non-zero helicity quantum numbers, as described in ref. [14].
In addition, our theoretical development applies to reactions treated by many other approximate theoretical techniques such as reduced dimensionality methods,[17, 18] e.g., the rotating-line-umbrella approximation for reactions of the type
A + BCD3(si = 0) → AB(vf, jf , mf = 0) + CD3(sf= 0)
where the labels si = 0 and sf = 0 indicate that the molecules BCD3 and CD3, respectively, are in their ground states.[17]
2. Weak version of Heisenberg’s S matrix program
Heisenberg’s original S matrix program (HSMP) is based on his fundamental insight that all the information needed to calculate collisional observables, such as DCSs, is contained within the S matrix.[10-13] No potential energy surface(s) is(are) necessary. It was originally hoped that general physical principles satisfied by the collision system, such as unitarity, causality and analyticity, could be used to determine the S matrix.[10-13] This hope has never been realised. To avoid this difficulty, we have introduced [14] and applied to the H + D2 and F + H2 reactions [14-16],a weak version of HSMP. Historical remarks on HSMP can be found in ref. 14. Note that we always work with a modified S matrix element in the following[1-4] denoted, 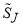 .
.
The wHSMP employs four general physical principles relevant to state-to-state chemical reactions.[14] They are used in our design strategy for the construction of the S matrix. The four general physical principles are:
(1)The forces responsible for chemical reactions are short ranged, of the order of 10−10 m. This implies 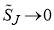 as
as 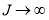 . In practice, there is a maximum value of J, denoted
. In practice, there is a maximum value of J, denoted , beyond which partial waves make a negligible numerical contribution to the PWS. N.b., this principle excludes reactions that are asymptotically Coulombic, for which the PWS is divergent.
, beyond which partial waves make a negligible numerical contribution to the PWS. N.b., this principle excludes reactions that are asymptotically Coulombic, for which the PWS is divergent.
(2) Conservation of probability holds. This implies the S matrix is unitary with 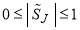 .
.
(3) Under semiclassical conditions, namely, 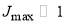 , we can continue the set of J-dependent S matrix elements, denoted
, we can continue the set of J-dependent S matrix elements, denoted 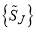 , to a smoothly varying function,
, to a smoothly varying function,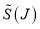 , with simple properties. In our applications,
, with simple properties. In our applications, 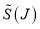 is an analytic function, i.e., one of class
is an analytic function, i.e., one of class 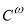 in the notation used for the continuity and differentiability of functions.[15]
in the notation used for the continuity and differentiability of functions.[15]
(4) In the classical limit, we require a head-on collision to correspond to backward (or rebound) scattering of the products.
Notice that Principle (3) was used in a weaker form in refs. [15] and [16], where 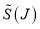 was allowed to be (i) a piecewise-continuous function (of class
was allowed to be (i) a piecewise-continuous function (of class 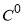 ), with simple properties for the pieces,or (ii) a piecewise-discontinuous function (of class
), with simple properties for the pieces,or (ii) a piecewise-discontinuous function (of class 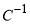 ), again with simple properties for the pieces.
), again with simple properties for the pieces.
3. Parametrization of the S matrix
Keeping the wHSMP principles of section 2 in mind, we use the same polar parametrization as ref. [4], and write 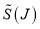 in the form
in the form
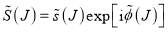 (1)
(1)
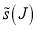 is positive or zero with
is positive or zero with  for
for 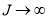 . We must choose
. We must choose 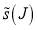 so that
so that 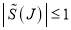 for all
for all 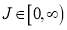 . Also
. Also 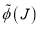 is a real scattering phase (or argument) and we evidently have,
is a real scattering phase (or argument) and we evidently have, 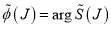 .
.
3A. Parametrization of 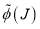
We use the same functional form for 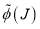 as previously.[4] Its parameters are held fixed in the results section 5. The quantum deflection function,
as previously.[4] Its parameters are held fixed in the results section 5. The quantum deflection function, 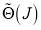 , is also important for the asymptotic theory of section 4. It is defined by
, is also important for the asymptotic theory of section 4. It is defined by
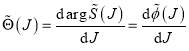 (2)
(2)
Note: the arg in Eq. (2) is not necessarily the principal value in order that the derivative be well defined.
As before, we choose 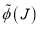 to be a cubic polynomial, which we can write in three equivalent forms: [4]
to be a cubic polynomial, which we can write in three equivalent forms: [4]
(1) The first form is an exact Taylor expansion about  :
:
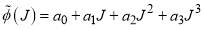 (3)
(3)
where  are four real phase parameters with
are four real phase parameters with 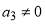 . The corresponding quantum defection function is
. The corresponding quantum defection function is
 (4)
(4)
. We choose two of the phase parameters in 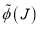 as follows:
as follows:
- The PWS DCSs and asymptotic DCSs are independent of the value of
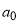 , so we choose
, so we choose 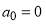 .
. - Equation (4) shows that,
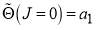 , i.e., in a classical picture, a head-on collision determines
, i.e., in a classical picture, a head-on collision determines 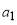 . So remembering Principle 4 of the wHSMP, we choose
. So remembering Principle 4 of the wHSMP, we choose 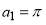 .
.
Figure 1 shows a plot of 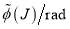 and
and 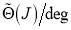 , both versus J, for the parameters used in our computations of section 5. Also marked on the graphs are quantities important for the asymptotic analysis in the next section. In particular, the real stationary points,
, both versus J, for the parameters used in our computations of section 5. Also marked on the graphs are quantities important for the asymptotic analysis in the next section. In particular, the real stationary points, 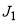 ,
, 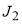 ,
, 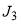 ,
, 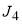 as well as the rainbow angular momentum variable,
as well as the rainbow angular momentum variable, 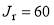 , and the glory angular momentum variables,
, and the glory angular momentum variables, 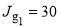 and
and 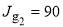 .
.
(2) For the second form, we use instead of a2 and a3, the more physically meaningful variables, (i) 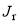 , the rainbow angular momentum variable which satisfies,
, the rainbow angular momentum variable which satisfies, 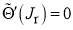 , and (ii)
, and (ii) 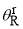 , the rainbow angle which satisfies
, the rainbow angle which satisfies  . Illustrations of these quantities are given in Figure 1. We have [4]
. Illustrations of these quantities are given in Figure 1. We have [4]
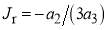
and
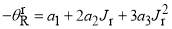
The cubic phase can then be written in the 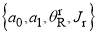 representation as
representation as
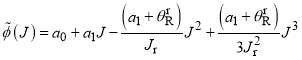 (5)
(5)
together with
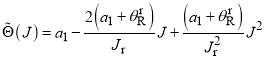 (6)
(6)
(3) The third form makes an exact Taylor expansion of 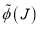 in Eq. (5) about the point
in Eq. (5) about the point 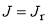 . We have
. We have

together with
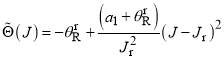
Note that 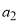 is always negative and
is always negative and 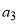 is always positive; this is because
is always positive; this is because 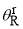 ,
, 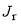 and
and 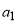 are all positive in our computations.
are all positive in our computations.
3B. Parametrization of 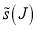
We write 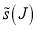 as the sum of two contributions:
as the sum of two contributions:
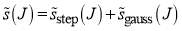 (7)
(7)
In Eq. (7), 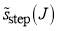 is a smooth step function given by [4, 14]
is a smooth step function given by [4, 14]
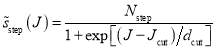 (8)
(8)
where 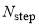 is as a normalization factor,
is as a normalization factor, 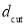 acts as a “diffuseness” parameter in J space, and
acts as a “diffuseness” parameter in J space, and 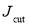 is the “cut off” value of J. The quantities,
is the “cut off” value of J. The quantities,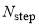 ,
, 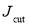 and
and 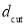 are positive, although not necessarily integers.
are positive, although not necessarily integers.
The second term in Eq. (7) is a gaussian (or bell-shaped) function of J defined by
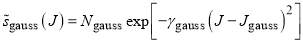 (9)
(9)
In Eq. (9), 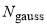 acts as a normalization factor,
acts as a normalization factor, 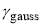 determines the width in J space and
determines the width in J space and 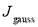 determines the position of the maximum of the gaussian curve in J space. In addition,
determines the position of the maximum of the gaussian curve in J space. In addition, 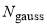 ,
, 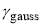 and
and 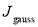 are positive, although not necessarily integers.
are positive, although not necessarily integers.
Figure 2 (left-hand column) shows plots of 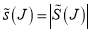 versus J for the five parametrizations, A – E, used in section 5.
versus J for the five parametrizations, A – E, used in section 5.
4. Theoretical methods
We use the same theoretical methods and working equations as in our companion paper [4]; so in this section we briefly summarize the techniques used, highlight important aspects of the theory and establish our notation.
4A. Partial Wave Theory
Our starting point is the Legendre PWS for the scattering amplitude, , given by
, given by
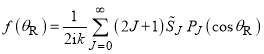 (10)
(10)
where k is the initial translational wavenumber, and 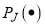 is a Legendre polynomial of degree J. Also,
is a Legendre polynomial of degree J. Also,  is the reactive scattering angle, which is defined as the angle between the incoming A atom and the outgoing AB molecule in the centre-of-mass collision system. The dependence of
is the reactive scattering angle, which is defined as the angle between the incoming A atom and the outgoing AB molecule in the centre-of-mass collision system. The dependence of 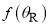 ,
, 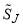 (and related quantities) on
(and related quantities) on 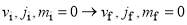 has been omitted for notational simplicity from Eq. (10), and below, as has the label
has been omitted for notational simplicity from Eq. (10), and below, as has the label 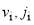 from k. In addition, we omit the channel label “reactive” from
from k. In addition, we omit the channel label “reactive” from 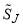 etc., so our results are not relevant for the elastic/inelastic channel. The full DCS is then given by
etc., so our results are not relevant for the elastic/inelastic channel. The full DCS is then given by
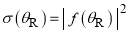 (11)
(11)
We shall see that the full DCS often exhibits complicated oscillatory structures. A powerful method to help understand these structures is an exact decomposition of  into the sum of nearside and farside subamplitudes.[19-21] We use the Fuller decomposition [22] and write
into the sum of nearside and farside subamplitudes.[19-21] We use the Fuller decomposition [22] and write
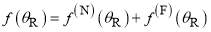 (12)
(12)
with
 (13)
(13)
where the 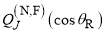 are travelling Legendre functions defined by (for
are travelling Legendre functions defined by (for 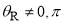 )
)
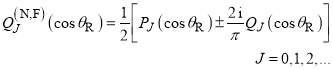 (14)
(14)
and 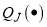 is a Legendre function of the second kind of degree J. The corresponding N, F DCSs are defined by (for
is a Legendre function of the second kind of degree J. The corresponding N, F DCSs are defined by (for 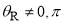 )
)
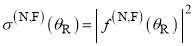
The fundamental identity for full and N,F DCSs is [19-21]
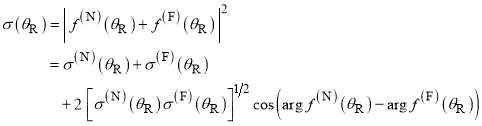 (15)
(15)
Although the decomposition (12) – (14) is mathematically exact, there is no guarantee that it is physically meaningful. However it is known that a resummation of the PWS (10) can significantly improve the physical effectiveness of a NF decomposition; this process is known as “cleaning”. [4,14-17,23-27] A detailed account of resummation theory for a Legendre PWS has been given by Totenhofer et al.[27]
A recent review of NF theory has been presented by Child, [28]while shorter reviews can be found in refs.29-32. Recent applications of NF techniques have provided insights into the dynamics of: the CH4 + Cl → CH3 + HCl reaction, [17] the SN2 Cl¯ + CH3Br → ClCH3 + Br¯ reaction, [33] four complex-mode reactions [34] and the forward- angle scattering of the H + HD → H2 + D reaction.[35]
4B. Asymptotic (semiclassical) rainbow representations
Here we outline the asymptotic (semiclassical ≡ SC) techniques that we use for the N and F scattering. We write the SC full scattering amplitude as
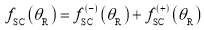 (16)
(16)
The corresponding full SC DCS is
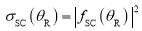 (17)
(17)
and the N and F SC DCSs are given by
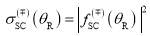
Note we use the superscripts,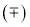 , to label the N and F SC subamplitudes respectively; this is to avoid confusion with the corresponding PWS subamplitudes. The SC theory uses the continuation of
, to label the N and F SC subamplitudes respectively; this is to avoid confusion with the corresponding PWS subamplitudes. The SC theory uses the continuation of 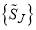 , with J = 0, 1, 2,…, to real values of J, which we denote by
, with J = 0, 1, 2,…, to real values of J, which we denote by 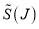 , i.e., the S matrix elements are now considered to be a continuous function of the total angular momentum variable.
, i.e., the S matrix elements are now considered to be a continuous function of the total angular momentum variable.
Firstly, we consider the F scattering, for which the stationary phase condition is [4]
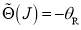 . (18)
. (18)
Figure 1(b) shows Eq. (18) has two real roots for a given value of 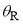 , provided
, provided 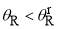 ; this corresponds to the bright side of the rainbow. The stationary points are denoted
; this corresponds to the bright side of the rainbow. The stationary points are denoted 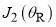 and
and 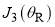 , which coalesce at
, which coalesce at  . In this angular region we use the uniform Airy approximation, which is denoted in a systematic notation by SC/F/uAiry, or for short, uAiry.[4] It allows for the proximity of
. In this angular region we use the uniform Airy approximation, which is denoted in a systematic notation by SC/F/uAiry, or for short, uAiry.[4] It allows for the proximity of 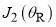 and
and 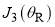 as
as 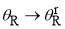 . When
. When 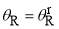 , the uAiry approximation becomes numerically indeterminate. On the dark side of the rainbow where
, the uAiry approximation becomes numerically indeterminate. On the dark side of the rainbow where 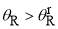 , the roots of Eq. (18) become complex valued, which are more awkward to handle.
, the roots of Eq. (18) become complex valued, which are more awkward to handle.
To avoid these difficulties, we use the transitional Airy approximation for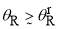 , which is denoted SC/F/tAiry, or tAiry for short.[4] The tAiry approximation only depends on the properties of
, which is denoted SC/F/tAiry, or tAiry for short.[4] The tAiry approximation only depends on the properties of 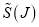 at
at  .
.
Secondly, we consider the N scattering, for which the stationary phase condition is [4]
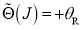 (19)
(19)
Figure 1(b) shows the stationary points, 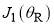 and
and 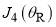 , are well separated from each other, so we can use the primitive semiclassical approximation at each point and write [4]
, are well separated from each other, so we can use the primitive semiclassical approximation at each point and write [4]
 (20)
(20)
In a systematic notation, Eq. (20) is written, SC/N/PSA, or PSA for short; with PSA1 and PSA4 being used for the individual SC sub-subamplitudes. In practice, we shall see that only one of our parametrizations, (namely D) in section 5 needs the PSA at 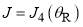 (i.e., PSA4) because the
(i.e., PSA4) because the 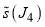 are negligible for the other parametrizations.
are negligible for the other parametrizations.
The full asymptotic (SC) DCS is then given by
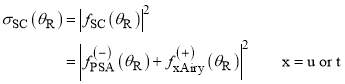
We also note that:
- Comparing the SC N, F DCSs with the PWS N, F DCSs provides an important test of the physical reliability of the Fuller PWS N, F decomposition in Eqs. (12) – (14), or the corresponding equations starting with the resummed PWS.
- It is also useful to have the explicit formulae for the stationary points. They are [4]
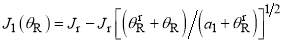 (21)
(21)
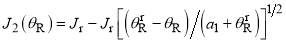 (22)
(22)
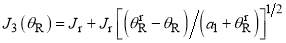 (23)
(23)
 (24)
(24)
Equations (21) and (24) are the real N roots of 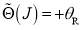 , whilst Eqs. (22) and (23) are the real F roots of
, whilst Eqs. (22) and (23) are the real F roots of 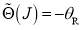 .
.
- There is a simple formula for the period of the NF diffraction oscillations in the DCS when just
 and
and 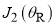 contribute to the scattering, as occurs in forward glory scattering. This formula is given by Eq. (50) of ref. 26, namely
contribute to the scattering, as occurs in forward glory scattering. This formula is given by Eq. (50) of ref. 26, namely
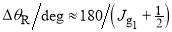 (25)
(25)
where  is the forward glory angular momentum variable shown in Figure 1. Notice that Eq. (25) is independent of
is the forward glory angular momentum variable shown in Figure 1. Notice that Eq. (25) is independent of 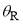 . Since we always have in our calculations,
. Since we always have in our calculations, 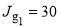 , Eq. (25) yields,
, Eq. (25) yields, 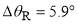 . Conversely, if we find a PWS DCS where
. Conversely, if we find a PWS DCS where 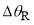 varies with
varies with 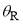 , and is much different from the simple result of Eq. (25), then this is a hint that other stationary points are contributing to the SC scattering.
, and is much different from the simple result of Eq. (25), then this is a hint that other stationary points are contributing to the SC scattering.
5. Results and discussion
We recall from Section 3, that 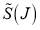 contains 10 parameters. They are:
contains 10 parameters. They are: 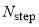 , Jcut, dcut in
, Jcut, dcut in  ;
;  ,
,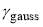 ,
,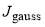 in
in 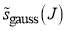 ; and
; and 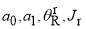 in the cubic phase. In the calculations that follow, we always keep the parameters in
in the cubic phase. In the calculations that follow, we always keep the parameters in 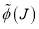 fixed, with the values,
fixed, with the values, 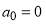 ,
, 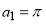 ,
, 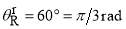 ,
, 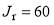 . These values were also used previously by us for one of our phases in the varying-the-phase calculations, but keeping the modulus fixed (see Table 1 of ref. [4]).
. These values were also used previously by us for one of our phases in the varying-the-phase calculations, but keeping the modulus fixed (see Table 1 of ref. [4]).
Table 1 reports the values of the six parameters in  and
and 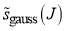 employed in our computations. We report results for five sets of parameters: the resulting parametrizations are denoted A, B, C, D, E. Note that parametrization A contains
employed in our computations. We report results for five sets of parameters: the resulting parametrizations are denoted A, B, C, D, E. Note that parametrization A contains  only and the phase, whilst parametrization E comprises
only and the phase, whilst parametrization E comprises 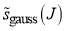 and the phase only. Sometimes, we will add a subscript, A, B, C, D, E, to
and the phase only. Sometimes, we will add a subscript, A, B, C, D, E, to 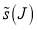 or
or 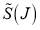 to distinguish different parametrizations, e.g.,
to distinguish different parametrizations, e.g., 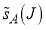 .
.
Plots of 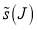 (or equivalently,
(or equivalently,  ) versus J for the five parametrizations are shown in the left-hand column of Figure 2. The shapes of the curves are typical of many state-to-state chemical reactions. For example, in Figure 2a, the smooth decline in
) versus J for the five parametrizations are shown in the left-hand column of Figure 2. The shapes of the curves are typical of many state-to-state chemical reactions. For example, in Figure 2a, the smooth decline in 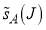 was used previously for the H + D2 reaction [14], whereas in Figure 2b the peak at larger J is typical of the F + H2 and CH4 + Cl reactions [16,17]. Table 1 shows that
was used previously for the H + D2 reaction [14], whereas in Figure 2b the peak at larger J is typical of the F + H2 and CH4 + Cl reactions [16,17]. Table 1 shows that 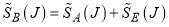 . However, we will see that this is not true for the corresponding DCSs displayed below, because of interference between the A and E subamplitudes.
. However, we will see that this is not true for the corresponding DCSs displayed below, because of interference between the A and E subamplitudes.
The right-hand column of Figure 2 displays the corresponding graphs of 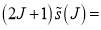
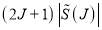 versus J. These graphs are useful because they show the magnitude of the numerical contribution of the modified S matrix to the DCS; e.g., Figure 2d, shows that
versus J. These graphs are useful because they show the magnitude of the numerical contribution of the modified S matrix to the DCS; e.g., Figure 2d, shows that 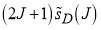 extends into the second nearside region.
extends into the second nearside region.
As well as the five parametrizations A–E, we have carried calculations for many other parametrizations, F, G, H,… They show similar results to the five parametrizations we discuss. In all cases we have performed PWS calculations for resummations orders [4,14-17, 23-27] of r = 0 (no resummation, i.e., Eq. (10)), and r = 1,2,3. We find the biggest cleaning effect on the PWS N, F DCSs occurs on going from r = 0 to r = 1. Additional resummations to r = 2 and r = 3 have a smaller cleaning effect. Thus in Sections 5A-5E, we shall only show PWS N, F DCS results for r = 1.
We have also computed values of the full and N, F local angular momenta [23-25,36], 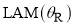 , for the SC theory as well as for r = 0,1,2,3, for the PWS theory. They are not shown, because the LAM results are consistent with our DCS results.
, for the SC theory as well as for r = 0,1,2,3, for the PWS theory. They are not shown, because the LAM results are consistent with our DCS results.
Table 1. Values of the S matrix parameters. Every parametrization has the same cubic phase with 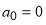 ,
, 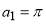 ,
, 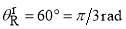 and
and 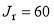 .
.
| Parametrization | 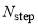 |
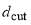 |
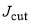 |
Ngauss | γgauss | Jgauss |
| A | 0.03 | 5 | 65 | – | – | – |
| B | 0.03 | 5 | 65 | 0.03 | 0.01 | 40 |
| C | 0.03 | 5 | 65 | 0.03 | 0.01 | 70 |
| D | 0.03 | 5 | 65 | 0.03 | 0.01 | 90 |
| E | – | – | – | 0.03 | 0.01 | 40 |
In the following, we shall show dimensionless DCSs (denoted dDCSs), defined as 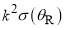 , in our logarithmic plots. In every case we have also made linear plots. We find logarithmic plots are the more meaningful since they allow the reader to see clearly the contribution of the farside scattering to the dark side of rainbows.
, in our logarithmic plots. In every case we have also made linear plots. We find logarithmic plots are the more meaningful since they allow the reader to see clearly the contribution of the farside scattering to the dark side of rainbows.
Our figures adopt the following colour conventions for the dDCS curves in the 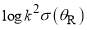 versus
versus  graphs:
graphs:
- Full PWS: solid black.
- N PWS/r=1: solid red.
- F PWS/r=1: solid blue.
- Full SC: solid green.
- N SC/PSA: dashed yellow.
- F SC/uAiry: solid purple.
- F SC/tAiry: dashed purple.
On every graph, solid pink arrows mark the value of the rainbow angle, 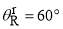 .
.
5A. dDCSs for ParametrizationA
Figure 3 displays dDCSs for the smooth-step function, 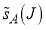 of Figure 2a, in the form of logarithmic plots for
of Figure 2a, in the form of logarithmic plots for 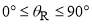 . The PWS curve in Figure 3a shows the characteristic shape of a primary rainbow for
. The PWS curve in Figure 3a shows the characteristic shape of a primary rainbow for 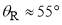 , accompanied by diffraction (high frequency) oscillations extending out to
, accompanied by diffraction (high frequency) oscillations extending out to 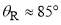 . The PWS N, F dDCSs show that the diffraction oscillations arise from interference of the corresponding subamplitudes using Eq. (15) generalized to r = 1. [36] The F contribution dominates the scattering for
. The PWS N, F dDCSs show that the diffraction oscillations arise from interference of the corresponding subamplitudes using Eq. (15) generalized to r = 1. [36] The F contribution dominates the scattering for 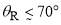 , with a change in mechanism at
, with a change in mechanism at 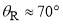 from F-dominant to N-dominant.
from F-dominant to N-dominant.
It is difficult to decide from the full PWS dDCS in Figure 3a whether there are supernumerary rainbows present or not? Here an examination of the PWS F dDCS is very helpful, as it is seen to possess several weak oscillations. These suggest there are indeed weak supernumerary rainbows in the full PWS dDCS.
Figure 3b compares the SC N, F dDCSs with the corresponding PWS N, F dDCSs. We see that the SC and PWS curves agree closely. This is an important result as it demonstrates that the Fuller NF decomposition of Eqs. (12) − (14) is physically meaningful. In particular, it proves that the oscillations in the PWS F dDCS correspond to a primary rainbow and weak supernumeraries. Note that our SC N analysis of Eq. (20) uses only the 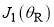 stationary point, since Figure 2a shows that
stationary point, since Figure 2a shows that  and
and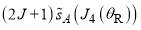 are negligible.
are negligible.
The full SC and PWS dDCSs are compared in Figure 3c. We see very good agreement between the two curves. Thus we have achieved a comprehensive physical and mathematical (generic) understanding of the rainbow and diffraction effects for parametrization A. Finally we note that the period of the full PWS interference oscillations is 5.9°, 5.3°, 4.8° close to  = 30°,50°,70° respectively. This tells us that there are more stationary points than
= 30°,50°,70° respectively. This tells us that there are more stationary points than 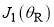 and
and 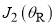 contributing to the forward scattering, since Eq. (25) predicts
contributing to the forward scattering, since Eq. (25) predicts  5.9°, independent of
5.9°, independent of 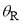 .
.
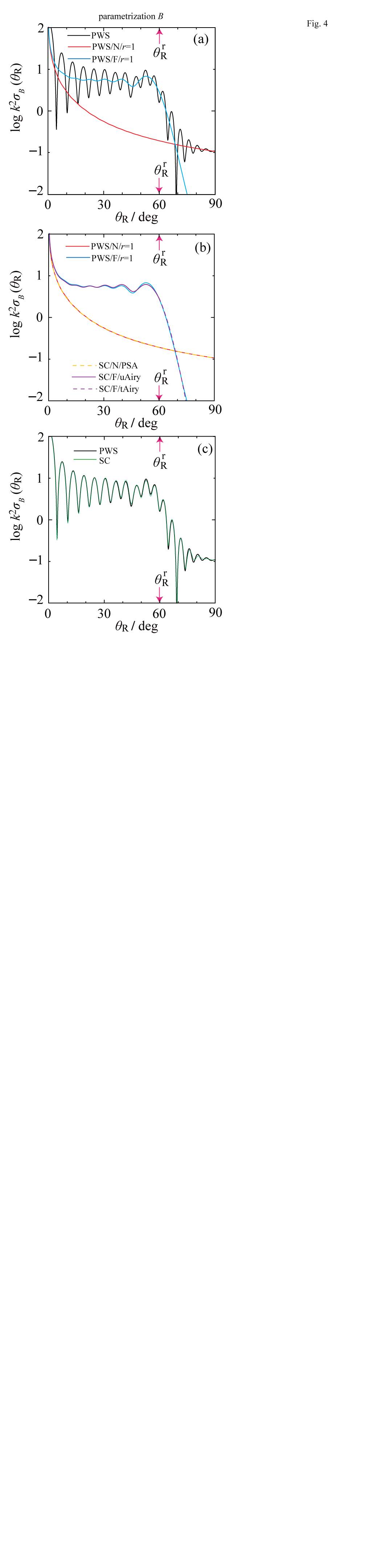
5B. dDCSs for ParametrizationB
Next we consider parametrization B, for which 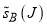 and
and 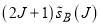 are plotted in Figure 2b, left- and right-hand columns, respectively. We see that the
are plotted in Figure 2b, left- and right-hand columns, respectively. We see that the 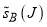 curve, which possesses a pronounced peak at
curve, which possesses a pronounced peak at 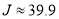 , is qualitatively different from
, is qualitatively different from 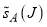 .
.
The corresponding PWS and SC dDCSs are displayed in Figure 4 as logarithmic plots for 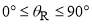 . The full PWS dDCS in Figure 4a is dominated by diffraction oscillations which arise from N-F interference (see the N and F curves in Figures 4a and 4b). Now there are no obvious rainbows or supernumerary rainbows in the full PWS dDCS. However the F PWS and F SC dDCSs reveal the presence of a weak primary rainbow accompanied by several weak supernumeraries. As in the case for parametrization A, our SC N calculation uses only the
. The full PWS dDCS in Figure 4a is dominated by diffraction oscillations which arise from N-F interference (see the N and F curves in Figures 4a and 4b). Now there are no obvious rainbows or supernumerary rainbows in the full PWS dDCS. However the F PWS and F SC dDCSs reveal the presence of a weak primary rainbow accompanied by several weak supernumeraries. As in the case for parametrization A, our SC N calculation uses only the 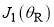 stationary point, since Figure 2b shows that
stationary point, since Figure 2b shows that 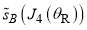 and
and 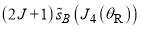 are negligible.
are negligible.
Our SC N and F analysis is confirmed in Figure 4c for the full dDCS, which shows very good agreement for the PWS and SC curves. In particular we have shown the presence of hidden primary and supernumerary rainbows for parametrization B.
Also note that the period of the full PWS interference oscillations is 5.8°, 5.3°, 4.8° for 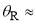 30°, 50°, 70° respectively. This again tells us that there are more stationary points than
30°, 50°, 70° respectively. This again tells us that there are more stationary points than 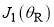 and
and 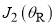 contributing to the forward scattering, since Eq. (25) predicts
contributing to the forward scattering, since Eq. (25) predicts  5.9°, independent of
5.9°, independent of 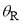 .
.
5C. dDCSs for ParametrizationC
Figure 2c shows the plot of 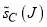 versus J. Compared to
versus J. Compared to 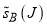 , we see the maximum of
, we see the maximum of 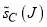 has moved to
has moved to 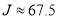 . Figure 5 displays the PWS and SC dDCSs as logarithmic plots for
. Figure 5 displays the PWS and SC dDCSs as logarithmic plots for 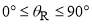 . Unlike the previous two examples, the full PWS dDCS in Figure 5a displays a prominent primary rainbow, together with noticeable supernumeraries, accompanied by N-F diffraction oscillations. The rainbows are clearly visible in the F PWS and F SC plots in Figure 5b. As previously, our SC N calculation uses only the
. Unlike the previous two examples, the full PWS dDCS in Figure 5a displays a prominent primary rainbow, together with noticeable supernumeraries, accompanied by N-F diffraction oscillations. The rainbows are clearly visible in the F PWS and F SC plots in Figure 5b. As previously, our SC N calculation uses only the 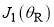 stationary point; Figure 2c shows that
stationary point; Figure 2c shows that 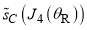 and
and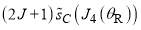 are negligible.
are negligible.
Our SC N and F computations for the pronounced primary and supernumerary rainbows in the full dDCS are confirmed in Figure 5c; there is very good agreement between the PWS and SC curves.
Finally we note that the period of the PWS interference oscillations is 5.4°, 5.2°, 4.4° close to  = 30°,50°,70° respectively. Once again, this suggests that there are more stationary points than
= 30°,50°,70° respectively. Once again, this suggests that there are more stationary points than 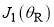 and
and 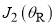 contributing to the forward scattering, since Eq. (25) gives
contributing to the forward scattering, since Eq. (25) gives  5.9°, independent of
5.9°, independent of 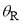 .
.
The graph of 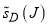 versus J in Figure 2d exhibits two new features. (i) There is a local minimum at
versus J in Figure 2d exhibits two new features. (i) There is a local minimum at 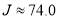 , in addition to the maximum at
, in addition to the maximum at 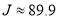 , (ii)
, (ii)  and
and 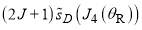 are no longer negligible, i.e., the first and second N regions contribute to the scattering.
are no longer negligible, i.e., the first and second N regions contribute to the scattering.
Next we examine Figure 6, which shows logarithmic plots of the dDCSs for 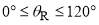 . We see the PWS dDCS in Figure 6a possesses oscillations out to
. We see the PWS dDCS in Figure 6a possesses oscillations out to 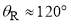 . There is visible a primary rainbow at
. There is visible a primary rainbow at 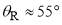 and a supernumerary rainbow at
and a supernumerary rainbow at 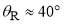 . At smaller angles, the dDCS exhibits rapidly-varying irregular oscillations. How are we to understand this complicated dDCS?
. At smaller angles, the dDCS exhibits rapidly-varying irregular oscillations. How are we to understand this complicated dDCS?
Firstly, we examine the F PWS dDCS and F SC dDCS in Figure 6b, which are seen to agree closely. We observe that the F scattering possesses a pronounced primary rainbow and five supernumeraries, which extend down to 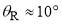 . Secondly, we inspect the N PWS and N SC curves in Figure 6b (which are also in close agreement). They possess regular oscillations extending out to
. Secondly, we inspect the N PWS and N SC curves in Figure 6b (which are also in close agreement). They possess regular oscillations extending out to 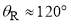 , whereas previously in Figures 3-5, the N curves are monotonic. The SC analysis reveals that the oscillations arise from the interference of the sub-subamplitudes associated with the stationary points,
, whereas previously in Figures 3-5, the N curves are monotonic. The SC analysis reveals that the oscillations arise from the interference of the sub-subamplitudes associated with the stationary points, 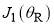 and
and 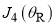 , i.e., the N scattering receives contributions from the first and second N regions.
, i.e., the N scattering receives contributions from the first and second N regions.
The full PWS dDCSs and full SC dDCSs are compared in Figure 6c; they are seen to agree closely. It is remarkable that the SC analysis provides a relatively simple explanation for the complicated PWS dDCS in terms of the four interfering stationary points, 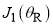 ,
, 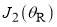 ,
, 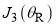 ,
, 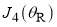 . The simple formula (25) for the period of the oscillations no longer applies.
. The simple formula (25) for the period of the oscillations no longer applies.
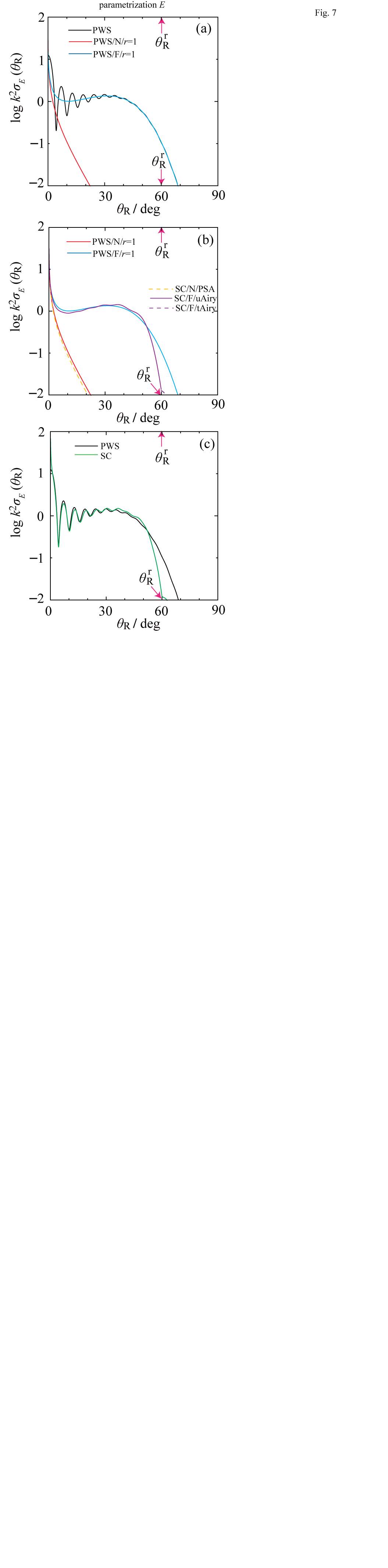
5E. dDCSs for ParametrizationE
Finally we consider parametrization E, for which 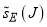 is a pure-gaussian function of J. Figure 2e shows that both
is a pure-gaussian function of J. Figure 2e shows that both 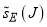 and
and 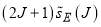 are very small at
are very small at 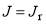 . This tells us that the sub-subamplitude for the scattering from
. This tells us that the sub-subamplitude for the scattering from 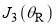 will be tiny. We then expect that the resulting rainbow in the dDCS will be miniscule, and in practice we cannot see it, even for
will be tiny. We then expect that the resulting rainbow in the dDCS will be miniscule, and in practice we cannot see it, even for 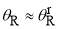 . This is confirmed by inspection of Figure 7a where the plot of the PWS dDCS versus
. This is confirmed by inspection of Figure 7a where the plot of the PWS dDCS versus 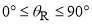 just shows diffraction oscillations at small angles,
just shows diffraction oscillations at small angles, 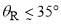 .
.
Figure 7b shows that the F PWS dDCS and the F SC dDCS do not exhibit rainbow oscillations. Since the N PWS dDCS and N SC dDCS agree closely, and are monotonic, we deduce that the small-angle diffraction oscillations arise from N-F interference of the corresponding subamplitudes. Figure 7c shows that the full PWS and SC dDCSs are in good agreement.
We note that the period of the PWS interference oscillations is 5.8°, 5.8°, 5.8° for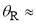 10°,20°,30° respectively, which is very close to the result from Eq. (25) of
10°,20°,30° respectively, which is very close to the result from Eq. (25) of  5.9° (independent of
5.9° (independent of 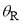 ), i.e., we expect just the stationary points
), i.e., we expect just the stationary points 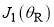 and
and 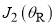 to contribute to the scattering in this angular range, which is the case.
to contribute to the scattering in this angular range, which is the case.
6. Conclusions
This paper has investigated the occurrence of pronounced and hidden rainbows in the state-to-state product dDCSs of chemical reactions. We used a novel theoretical approach, wHSMP; it does not employ a potential energy surface. Rather wHSMP uses four general physical principles for chemical reactions to suggest simple parametrized forms for the S matrix.
We used a realistic parametrization in which the modulus of the S matrix is the sum of a smooth-step function and a gaussian function, both functions of J; whilst the phase of the S matrix is a cubic polynomial in J. We varied the modulus and held the phase fixed. Our calculations complement and extend earlier work [4] in which the modulus is held fixed and the phase varied.
We then analysed five Legendre PWS dDCSs using NF PWS theory, including resummations of the PWS for r = 0, 1, 2, 3. We also applied full and NF SC (asymptotic) rainbow theories − in particular, the uAiry and tAiry approximations for the farside scattering. In every case we proved the existence of primary rainbows, supernumerary rainbows (both hidden and pronounced) and other interference effects. We obtained a comprehensive physical and mathematical (generic) understanding of structures in the angular scattering in terms of contributions from (up to) four real stationary points, 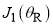 ,
, 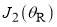 ,
, 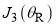 ,
, 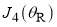 . In addition, we used the SC theory to demonstrate that the Fuller NF decomposition of the PWS is physically meaningful, as well as being mathematically exact.
. In addition, we used the SC theory to demonstrate that the Fuller NF decomposition of the PWS is physically meaningful, as well as being mathematically exact.
More generally, it is well established that rainbows occur in many different wave phenomena.[37-41] The present calculations, and our earlier work, [1-4] show that this is also true for reactive DCSs.
References
Xiahou C and Connor J N L 2009 A new rainbow: angular scattering of the F + H2(vi = 0, ji = 0) → FH(vf = 3, jf = 3) + H reaction J. Phys. Chem. A 113 15298-15306
Xiahou C, Connor J N L and Zhang D H 2011 Rainbows and glories in the angular scattering of the state-to-state F + H2 reaction at Etrans = 0.04088 eV Phys. Chem. Chem. Phys. 13 12981-12997
Xiahou C and Connor J N L 2014 The 6Hankel asymptotic approximation for the uniform description of rainbows and glories in the angular scattering of state-to-state chemical reactions: derivation, properties and applications Phys. Chem. Chem. Phys. 16 10095-10111
Shan X, Xiahou C and Connor J N L 2018 Rainbows, supernumerary rainbows and interference effects in the angular scattering of chemical reactions: an investigation using Heisenberg’s S matrix programme Phys. Chem. Chem. Phys 20 819-836
Connor J N L 1980 Semiclassical theory of elastic scattering. In Semiclassical Methods in Molecular Scattering and Spectroscopy Proceedings of the NATO Advanced Study Institute held in Cambridge England in September 1979 Child, M S Editor (Dordrecht Netherlands: Reidel) pp 45–107
Child M S 2014 Semiclassical Mechanics with Molecular Applications, 2nd edition (Oxford UK: Oxford University Press) chap. 9 Atom-atom scattering
Balint-Kurti G G and Pavlov A P 2015 Theory of Molecular Collisions RSC Theoretical and Computational Chemistry Series No. 7 (Cambridge UK: Royal Society of Chemistry) chap. 2 Quantum theory of atom-atom elastic scattering.
Neumark D M, Wodtke A M, Robinson G N, Hayden C C and Lee Y T 1985 Molecular beam studies of the F + H2 reaction J. Chem. Phys. 82 3045-3066
Wang X, Dong W, Qiu M, Ren Z, Che L, Dai D, Wang X, Yang X, Sun Z, Fu B, Lee S-Y, Xu X and Zhang D H HF( = 3) 2009 Forward scattering in the F + H2 reaction: shape resonance and slow-down mechanism Proc. Nat. Acad. Sci. U.S.A. 105 6227-6231
= 3) 2009 Forward scattering in the F + H2 reaction: shape resonance and slow-down mechanism Proc. Nat. Acad. Sci. U.S.A. 105 6227-6231
Heisenberg W 1943 Die „beobachtbaren Gröβen“ in der Theorie der Elementarteilchen Zeit. Phys. 120 513-538. Part I. Reprinted in Werner Heisenberg, Gesammelte Werke=Collected Works, Series A, Part II, Original Scientific Papers=Wissenschaftliche Originalarbeiten Blum W, Dürr H-P and Rechenberg H Editors (Berlin Germany: Springer-Verlag) 1989 pp 611-636
Heisenberg W 1943 Die beobachtbaren Gröβen in der Theorie der Elementarteilchen II Zeit. Phys. 120 673-702. Part II. Reprinted in Werner Heisenberg, Gesammelte Werke=Collected Works, Series A, Part II, Original Scientific Papers=Wissenschaftliche Originalarbeiten Blum W, Dürr H-P and Rechenberg H Editors (Berlin Germany: Springer-Verlag) 1989 pp 637-666
Heisenberg W 1944 Die beobachtbaren Gröβen in der Theorie der Elementarteilchen. III. Zeit. Phys. 123 93-112. Part III. Reprinted in Werner Heisenberg, Gesammelte Werke=Collected Works, Series A, Part II, Original Scientific Papers=Wissenschaftliche Originalarbeiten Blum W, Dürr H-P and Rechenberg H Editors (Berlin Germany: Springer-Verlag) 1989 pp 667-686
Heisenberg W Die Behandlung von Mehrkörperproblemen mit Hilfe der η-Matrix [Die beobachtbaren Gröβen in der Theorie der Elementarteilchen. IV]. Unpublished paper. Part IV. Reprinted in Werner Heisenberg, Gesammelte Werke=Collected Works, Series A, Part II, Original Scientific Papers=Wissenschaftliche Originalarbeiten; Blum W, Dürr H-P and Rechenberg H Editors (Berlin Germany: Springer-Verlag) 1989 pp 687-698 (original manuscript dated 1944 by the editors)
Shan X and Connor J N L 2011 Angular scattering using parameterized S matrix elements for the H + D2(vi = 0, ji = 0) → HD(vf = 3, jf = 0) + D reaction: an example of Heisenberg’s S matrix programme Phys. Chem. Chem. Phys. 13 8392-8406
Shan X and Connor J N L 2012 Application of Heisenberg’s S matrix program to the angular scattering of the H + D2(vi = 0, ji = 0) → HD(vf = 3, jf = 0) + D reaction: piecewise S matrix elements using linear, quadratic, step-function and top-hat parametrizations J. Phys. Chem. A 116 11414-11426
Shan X and Connor J N L 2014 Application of Heisenberg’s S matrix program to the angular scattering of the state-to-state F + H2 reaction. J. Phys. Chem. A 118 6560-6573
Totenhofer A J, Connor J N L and Nyman G 2016 Angular scattering dynamics of the CH4 + Cl → CH3 + HCl reaction using nearside−farside, local angular momentum, and resummation theories J. Phys. Chem. B 120 2020-2032
Connor J N L and Child M S 1970 Differential cross sections for chemically reactive systems Mol. Phys. 18 653-679
Connor J N L, McCabe P, Sokolovski D and Schatz G C 1993 Nearside–farside analysis of angular scattering in elastic, inelastic and reactive molecular collisions Chem. Phys. Lett. 206 119-122
McCabe P and Connor J N L 1996 Nearside–farside analysis of differential cross sections: diffraction and rainbow scattering in atom–atom and atom–molecule rotationally inelastic sudden collisions J. Chem. Phys. 104 2297-2311
Dobbyn A J, McCabe P, Connor J N L and Castillo J F 1999 Nearside–farside analysis of state selected differential cross sections for reactive molecular collisions Phys. Chem. Chem. Phys. 1 1115-1124
Fuller R C 1975 Qualitative behavior of heavy-ion elastic scattering angular distributions Phys. Rev. C 12 1561-1574
Anni R, Connor J N L and Noli C 2002 Improved nearside–farside method for elastic scattering amplitudes Phys. Rev. C 66 044610
Anni R, Connor J N L and Noli C 2004 Improved nearside–farside decomposition of elastic scattering amplitudes Khim. Fiz. 23 (No. 2) 6-12. Also available at: http://arXiv.org/abs/physics/0410266
Connor J N L and Anni R 2004 Local angular momentum-local impact parameter analysis: a new tool for understanding structure in the angular distributions of chemical reactions Phys. Chem. Chem. Phys. 6 3364-3369
Xiahou C and Connor J N L 2006 Theory of forward glory scattering for chemical reactions: accuracy of semiclassical approximations using a J-shifted Eckart parameterization for the scattering matrix element Mol. Phys. 104 159-175
Totenhofer A J, Noli C and Connor J N L 2010 Dynamics of the I + HI → IH + I reaction: application of nearside-farside, local angular momentum and resummation theories using the Fuller and Hatchell decompositions Phys. Chem. Chem. Phys. 12 8772-8791
Child M S 2014 Nearside-farside interpretation of differential cross-sections. In Semiclassical Mechanics with Molecular Applications, 2nd edition (Oxford UK: Oxford University Press) section 11.2
Schatz G C 1998 Quantum effects in gas-phase bimolecular collision processes: from state-to-state properties to microcanonical averages. In Advances in Classical Trajectory Methods Hase W L Editor (Stamford CT USA: JAI Press) Vol. 3 pp 205-229
Nyman G and Yu H-G 2000 Quantum theory of bimolecular chemical reactions Rep. Prog. Phys. 63 1001-1059
Connor J N L, 2009 Shan X, Totenhofer A J and Xiahou C New theoretical methods for understanding chemical reactions in the energy and time domains. In Multidimensional Quantum Mechanics with Trajectories Shalashilin D V and de Miranda M P Editors (Warrington Daresbury Laboratory UK: Collaborative Computational Project on Molecular Quantum Dynamics (CCP6)) pp 38-47. ISBN 978-0-9545289-8-0
Connor J N L 2015 Methods for understanding the angular scattering of chemical reactions. VIRT&L-COMM, Special Issue pp 1–40. ISSN 2779-8773. Also available at: http://www.hpc.unipg.it/ojs/index.php/virtlcomm/article/view/83
Hennig C and Schmatz S 2015 Mechanisms of SN2 reactions: insights from a nearside/farside analysis Phys. Chem. Chem. Phys. 17 26670-26676
Hankel M and Connor J N L 2015 Nearside-farside, local angular momentum and resummation theories: useful tools for understanding the dynamics of complex-mode reactions AIP Advances 5 077160
Yuan D, Yu S, Chen W, Sang J, Luo C, Wang T, Xu X, Casavecchia P, Wang X, Sun Z, Zhang D H and Yang X 2018 Direct observation of forward-scattering oscillations in the H + HD → H2 + D Reaction Nature Chem. 10 653-658
Monks P D D, Xiahou C and Connor J N L2006Local angular momentum–local impact parameter analysis: derivation and properties of the fundamental identity, with applications to the F + H2, H + D2, and Cl + HCl chemical reactions J. Chem. Phys. 125 133504
Sokolovski D and Msezane A Z 2004 Semiclassical complex angular momentum theory and Padé reconstruction of resonances, rainbows and reaction thresholds Phys. Rev. A 70 032710
Nešković N Editor Rainbows and Catastrophes Proceedings of the Workshop on Rainbow Scattering Cavtat, Yugoslavia, 14–16 Aug 1989 (Belgrade Yugoslavia: Boris Kidrić Institute of Nuclear Sciences)
Adam J A 2002 The Mathematical Physics of Rainbows and Glories Phys. Rep. 356 229-365
Adam J A 2017 Rays, Waves, and Scattering: Topics in Classical Mathematical Physics (Princeton USA: Princeton University Press)
Nešković N, Petrović S and Ćosić M 2017 Rainbows. In Rainbows in Channeling of Charged Particles in Crystals and Nanotubes Nešković N, Petrović S and Ćosić M Editors (Cham Switzerland: Springer) Lecture Notes in Nanoscale Science and Technology, 25 Chap. 1
Figure Captions
Figure 1. Black solid curves with 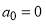 and
and  : (a)
: (a) 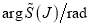 versus J, (b) quantum deflection function
versus J, (b) quantum deflection function 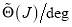 versus J. In (b), The red dashed lines and arrows indicate
versus J. In (b), The red dashed lines and arrows indicate 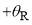 , as well as
, as well as 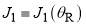 and
and 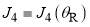 for the nearside scattering. The blue dashed lines and arrows indicate
for the nearside scattering. The blue dashed lines and arrows indicate 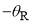 , as well as
, as well as 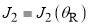 and
and 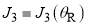 , for the farside scattering. In (a) and (b), the pink dashed lines and arrows indicate the rainbow angular momentum variable,
, for the farside scattering. In (a) and (b), the pink dashed lines and arrows indicate the rainbow angular momentum variable,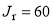 , which is located at the minimum of the
, which is located at the minimum of the 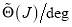 curve and satisfies,
curve and satisfies,  , where
, where 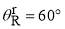 is the rainbow angle. The orange arrows indicate the two glory angular momentum variables,
is the rainbow angle. The orange arrows indicate the two glory angular momentum variables, 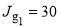 and
and 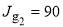 , which satisfy
, which satisfy 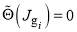 for i = 1, 2.
for i = 1, 2.
Figure 2. Plots of 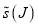 versus J (left hand column) and
versus J (left hand column) and 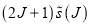 versus J (right hand column) for parametrizations A–E. The pink arrows and dashed lines indicate the rainbow angular momentum variable,
versus J (right hand column) for parametrizations A–E. The pink arrows and dashed lines indicate the rainbow angular momentum variable, 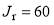 . The orange arrows and dashed lines indicate the two glory angular momentum variables,
. The orange arrows and dashed lines indicate the two glory angular momentum variables, 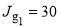 and
and 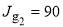 .
.
Figure 3. Plots of  versus
versus 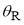 for parametrization A: (a) full PWS (black curve), N(r=1) PWS (red curve), F(r=1) PWS (blue curve). (b) N(r=1) PWS (red curve), F(r=1) PWS (blue curve), SC/N/PSA (dashed yellow curve), SC/F/uAiry (solid purple curve), SC/F/tAiry (dashed purple curve). (c) full PWS (black curve), full SC (green curve). The pink arrows denote the rainbow angle at
for parametrization A: (a) full PWS (black curve), N(r=1) PWS (red curve), F(r=1) PWS (blue curve). (b) N(r=1) PWS (red curve), F(r=1) PWS (blue curve), SC/N/PSA (dashed yellow curve), SC/F/uAiry (solid purple curve), SC/F/tAiry (dashed purple curve). (c) full PWS (black curve), full SC (green curve). The pink arrows denote the rainbow angle at 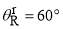 .
.
Figure 4. Plots of 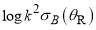 versus
versus 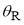 for parametrization B: (a) full PWS (black curve), N(r=1) PWS (red curve), F(r=1) PWS (blue curve). (b) N(r=1) PWS (red curve), F(r=1) PWS (blue curve), SC/N/PSA (dashed yellow curve), SC/F/uAiry (solid purple curve), SC/F/tAiry (dashed purple curve). (c) full PWS (black curve), full SC (green curve). The pink arrows denote the rainbow angle at
for parametrization B: (a) full PWS (black curve), N(r=1) PWS (red curve), F(r=1) PWS (blue curve). (b) N(r=1) PWS (red curve), F(r=1) PWS (blue curve), SC/N/PSA (dashed yellow curve), SC/F/uAiry (solid purple curve), SC/F/tAiry (dashed purple curve). (c) full PWS (black curve), full SC (green curve). The pink arrows denote the rainbow angle at 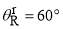 .
.
Figure 5. Plots of 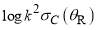 versus
versus 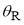 for parametrization C: (a) full PWS (black curve), N(r=1) PWS (red curve), F(r=1) PWS (blue curve). (b) N(r=1) PWS (red curve), F(r=1) PWS (blue curve), SC/N/PSA (dashed yellow curve), SC/F/uAiry (solid purple curve), SC/F/tAiry (dashed purple curve). (c) full PWS (black curve), full SC (green curve). The pink arrows denote the rainbow angle at
for parametrization C: (a) full PWS (black curve), N(r=1) PWS (red curve), F(r=1) PWS (blue curve). (b) N(r=1) PWS (red curve), F(r=1) PWS (blue curve), SC/N/PSA (dashed yellow curve), SC/F/uAiry (solid purple curve), SC/F/tAiry (dashed purple curve). (c) full PWS (black curve), full SC (green curve). The pink arrows denote the rainbow angle at 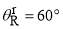 .
.
Figure 6. Plots of 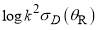 versus
versus 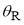 for parametrization D: (a) full PWS (black curve), N(r=1) PWS (red curve), F(r=1) PWS (blue curve). (b) N(r=1) PWS (red curve), F(r=1) PWS (blue curve), SC/N/PSA for branches 1 and 4 (dashed yellow curve), SC/F/uAiry (solid purple curve), SC/F/tAiry (dashed purple curve). (c) full PWS (black curve), full SC (green curve). The pink arrows denote the rainbow angle at
for parametrization D: (a) full PWS (black curve), N(r=1) PWS (red curve), F(r=1) PWS (blue curve). (b) N(r=1) PWS (red curve), F(r=1) PWS (blue curve), SC/N/PSA for branches 1 and 4 (dashed yellow curve), SC/F/uAiry (solid purple curve), SC/F/tAiry (dashed purple curve). (c) full PWS (black curve), full SC (green curve). The pink arrows denote the rainbow angle at 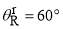 .
.
Figure 7. Plots of 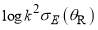 versus
versus 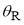 for parametrization E: (a) full PWS (black curve), N(r=1) PWS (red curve), F(r=1) PWS (blue curve). (b) N(r=1) PWS (red curve), F(r=1) PWS (blue curve), SC/N/PSA (dashed yellow curve), SC/F/uAiry (solid purple curve), SC/F/tAiry (dashed purple curve). (c) full PWS (black curve), full SC (green curve). The pink arrows denote the rainbow angle at
for parametrization E: (a) full PWS (black curve), N(r=1) PWS (red curve), F(r=1) PWS (blue curve). (b) N(r=1) PWS (red curve), F(r=1) PWS (blue curve), SC/N/PSA (dashed yellow curve), SC/F/uAiry (solid purple curve), SC/F/tAiry (dashed purple curve). (c) full PWS (black curve), full SC (green curve). The pink arrows denote the rainbow angle at 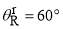 .
.



Cite This Work
To export a reference to this article please select a referencing stye below:
Related Services
View allRelated Content
All TagsContent relating to: "Chemistry"
Chemistry is a science involving the study of the elements and matter at the atomic and molecular level including their composition, structure, properties, behaviour, and how they react or combine.
Related Articles
DMCA / Removal Request
If you are the original writer of this dissertation and no longer wish to have your work published on the UKDiss.com website then please:




