Micromechanical Testing of Ti Alloys: Literature Review
Info: 7920 words (32 pages) Dissertation
Published: 9th Dec 2019
Tagged: ChemistryMicrobiology
Micromechanical testing of Ti alloys: Literature Review (Word Count: 4984)
1. Introduction
1.1. Overview
The crystal structure of Titanium is dependent on its temperature. At lower temperatures Ti possesses a Hexagonal Closed Packed (h.c.p.) structure known as the phase, whereas above approximately 890C, a phase transformation occurs to the Body Centred Cubic (b.c.c.) structure, known as the phase. Alloying additions act to retain a given phase, these are known as phase stabilisers. [1]
The majority of titanium alloys are used for aerospace applications, although the introduction of the total hip replacement, has seen titanium alloys used for the femoral stem [2]. However, the aerospace industry still dominates in the use of Titanium, largely due to the demanding environments seen by aerospace components justifying the cost of using Titanium. The key design criterion driving the use of Ti systems is weight saving, high strength to weight ratio and galvanic compatibility with carbon fibre. [3]
Of interest to this project is the metastable class of Ti alloys, notably Gum Metal. Which was first publicised by Saito et al. and generated considerable interest claiming a dislocation-free deformation mechanism in alloys Ti-12Ta-9Nb-3V-6Zr-O and Ti-23Nb-0.7Ta-2Zr-O (at.%). It was claimed that these compositions met three molecular orbital parameters resulting in a range of properties including, ultralow modulus, superelasticity, superplasticity and Elinvar/Invar properties. [4]
1.2. Supporting work
This project builds upon previous research by Luca Montanelli whose aim was to develop a series of Ti-based Gum metals that displayed superelasticity [5] without the aid of the molecular orbital parameters proposed by Saito et al. [4].
Molecular orbital numbers have been challenged as reliable indicators of phase stability. The alloy Ti-24V-28Zr-2O (at.%) possesses similar molecular orbital numbers as those reported by Saito et al. [4] but substitutes V with Nb. The two alloys displayed a stark contrast in mechanical properties, attributed to local chemistry variations existing in the alloys, which are the result of element partitioning during thermomechanical work. Which is not reflected in the bulk e/a value. Furthermore, the stability of the phase can vary between alloys exhibiting similar e/a values. The expression (C11-C12), where C11 and C22 are elastic constants in a cubic lattice, varies with phase stability [6]. The deformation mechanism of an alloy is influenced by the elastic constants of its lattice. Therefore, the deformation mechanism may vary between alloys displaying a similar e/a value due to differences in elastic constants. [7]
This is seen experimentally. The primary deformation mechanism of Ti-24V-28Zr-2O (at.%) was a martensitic transformation of to’’, a diffusionless transformation from the b.c.c structure to an orthorhombic one via cooperative movement of atoms. No such transformation was seen in Ti-12Ta-9Nb-3V-6Zr-O (at.%) and Ti-23Nb-0.7Ta-2Zr-O (at.%) [4]. The presence of oxygen, which can be vital to achieving the properties of Gum metal [4] is omitted from the calculations of all molecular orbital numbers partially owing to the fact that the values of Bo and Md for oxygen are unknown. Given the highly influential effect of oxygen [8] not factoring in its effect could be viewed as an oversight. Talling et al. proposed a revised design criteria for Gum Metal. Where alloys should exhibit low phase stability to encourage deformation via SIM. In addition to an interstitial content that acts to increase the strength of the phase and partially supress the to ’’ transformation. [7]
In place of the molecular orbital numbers, the Wechsler-Lieberman-Read (WLR) theory [9] and the Phenomenological Theory of Martensite Transformation (PTMT) [10] was adopted. Calculating several key aspects of the martensitic transformation including the martensite habit plane, twin plane and the martensite twin fractions using the lattice parameters of the austenite and martensite phases. These theories are based upon the condition that an interface of zero shear exists between the parent/child phases. To produce an alloy capable of undergoing multiple superelastic cycles the volume change (Vc) should be minimised between the parent/child phase, to limit defect accumulation. This volume change translates to distortions in WLR theory characterised by a distortion matrix of principal distortions 2,Leading to Equation 1 which relates Vc to the principal distortions, and thus yields a selection criterion. [5]
Vc=1+λ1-11+λ2-11+λ3-1-1 (Eq.1 [5])
The values of the principal distortions for a given alloy composition can be calculated from the lattice parameters of the austenite/martensitic phase. The austenite lattice parameter was estimated via a hard sphere Vegard’s Law model, using a weighted average of the atomic radii [11]. The martensite lattice parameters were estimated using linear regression from a selection of documented alloys [12]. With the lattice parameters known for an array of compositions, WLR theory could be used to calculate the principal distortions for each composition and also Vc . Four alloys were shortlisted for experimental characterisation, seen in Table 1. Two producing the lowest Vc and two alloys with a different Ta/Zr at.% displaying higher Vc values were selected to access to the influence of the Ta/Zr ratio on superelasticity. [5]
Table 1. Alloys selected for characterisation [5]
| Alloy Composition | Vc | λ1 | λ2 | λ3 |
| Ti-19Nb-12Ta-15Zr | 0.013 | 1.000 | 0.988 | 0.999 |
| Ti-19Nb-12Ta-12Zr | 0.013 | 1.003 | 0.990 | 0.994 |
| Ti-19Nb-10Ta-15Zr | 0.020 | 1.005 | 0.989 | 0.993 |
| Ti-19Nb-10Ta-12Zr | 0.023 | 1.005 | 0.989 | 0.993 |
2. Deformation twinning
Twinning is a process during which the symmetry of a crystal lattice becomes mirrored across a particular crystallographic plane. The associated displacement allows the accommodation of plastic strain both during annealing (annealing twins) and/or during mechanical shear (mechanical/deformation twins) where deformation via slip is restricted.
Such a transformation is described by a twin boundary (a mirror plane), where atoms located on either side are in mirror positions of one another. The mode of twinning is dependent on the crystal structure and occurs on a specific crystallographic plane and along a specific direction. In stable alloys, {112}<111> is a well-documented twinning mode [13]. However some metastable alloys undergo {332}<113> twinning [14][15][16]. Schematic diagrams of these twinning modes are seen in Figure 1. The mechanics of this twinning mode are subject to ongoing research. [17]
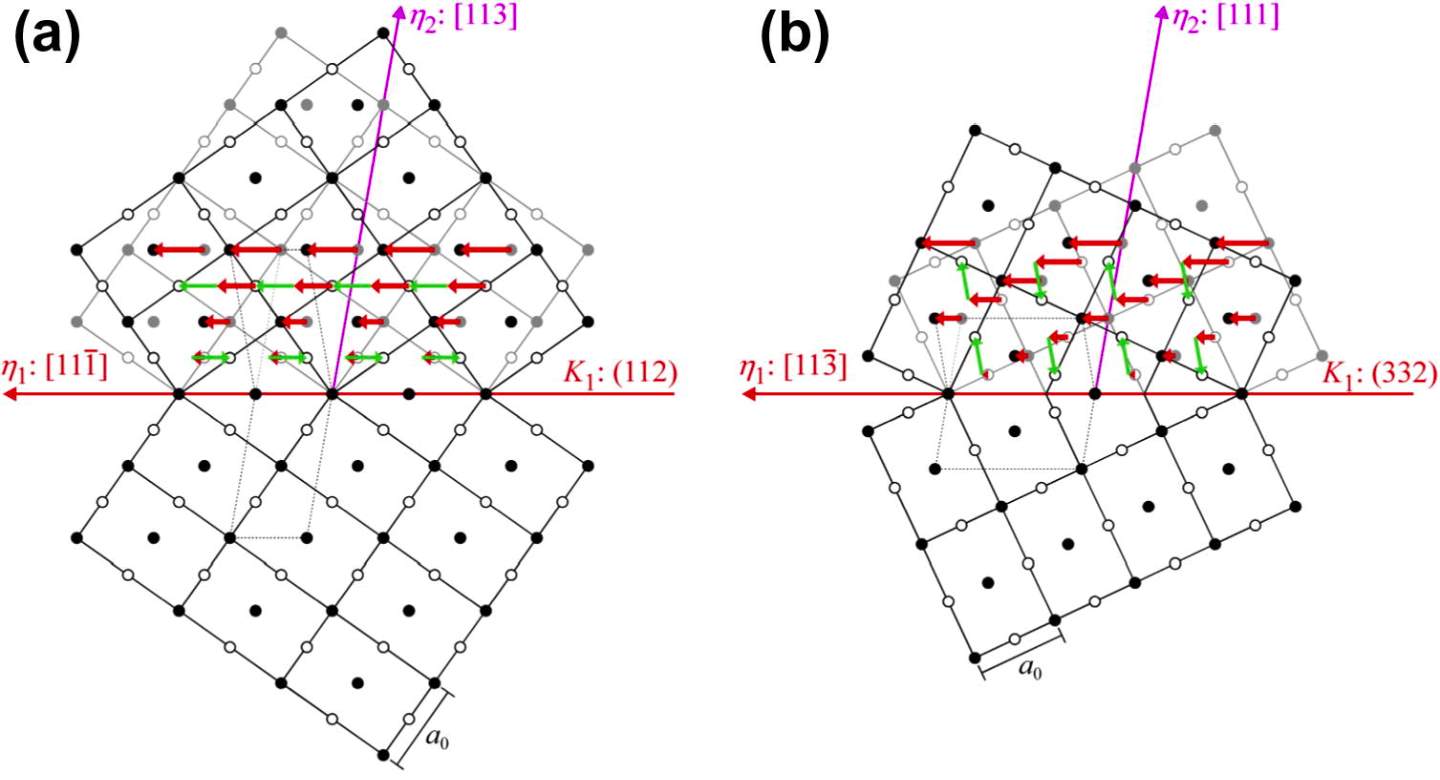
Figure 1. Diagrams of (a) (112)[11
1̅] twinning and (b) (332)[11
3̅] viewed along the (1
1̅0) projection in a b.c.c. crystal. Red and green arrows represent the direction of shear and shuffle respectively. Closed circles represent atoms in the projection plane, and open circle represent atoms in the next layer of the b.c.c. stacking sequence (0.7071 a0 above the projection) [15].
Current reports suggest that {332}<113> twinning is activated by instability in the metastable phase [15][16], with decreasing stability leading to a deformation mechanism transition from {110}<111> slip to {112}<111> twinning to {332}<113> twinning [18]. {112}<111> is a common twinning mode in stable b.c.c. alloys, while {332}<113> twinning has yet to be reported in stable b.c.c. alloys [19] [20].
{112}<111> twinning requires additional atomic shuffling in a metastable Ti lattice as this twinning mode can only move one-half of the atoms in the unit cell from untwinned to twinned sites. Furthermore, the lattice instability facilitates {332}<113> twinning due to a reduction in the shear modulus. {112}<111> twinning requires no shuffling of atomic planes in the stable b.c.c. structure, which offers an explanation as to why it is widely observed in stable b.c.c. metals. Lattice modulation occurs in metastable-alloys. Such modulation has been modelled by the shuffling of parallel adjacent {0
1̅1} planes along <011>directions, facilitated by the low shear modulus of the metastable- phase. Yielding a tetragonal structure seen in Figure 2. [15]

Figure 2. Diagrams of (a) the b.c.c structure and (b) the modulated b.c.c structure. The modulated structure can be modelled as a tetragonal structure (c) or (d). The blue lines indicate motif units of two atoms. The orange arrows indicate the direction and magnitude of shift undertaken by atoms during modulation [15].
{112}<111> twinning in the tetragonal structure requires a rearrangement of the motif units, making this mode unfavourable. The tetragonal structure favours {332}<113> twinning which requires smaller atomic displacements. This provides strong evidence that the instability of metastable facilitates the {332}<113> twinning mechanism. [15]
Recent work involving in-situ testing has found that, during the phase transformation from to ’’ in Ti-36Nb-2Ta-3Zr (wt.%), twins are produced to accommodate the strain produced by the difference (mismatch) in the crystal structures. The twinning shear strain, which relates to the movement of atoms during twining, was considerably smaller in this alloy than values reported in other metastable alloys, 0.2697 [16] compared to 0.3536 reported in Ti-40Nb-12.6Ta/Ti-26.9Nb-34.2Ta (wt.%) [21][22]. As such, a new twinning mechanism was proposed by which {332} twinning involves the shear of {211}T planes along <
1̅11>T directions, where the subscript “T” denotes the twin [16]. This differs from previous proposals that {332} twinning occurs via the movement of atoms on successive {332} planes along <113> directions, which requires a twinning shear of 0.3536 [21][22]. In addition, an ” aided twinning mechanism has been proposed, in which {332} twins nucleate in the newly-formed ” during deformation. The theory is supported by in-situ EBSD analysis of the ” receding into the twins as opposed to the matrix upon annealing at 900C for 30 minutes. [16]
The formation {332}<113> twins in metastable alloys remains an exciting area of research. Due to the wide range of compositions used to produce metastable alloysfurther work is required to understand the effects of alloying on {332}<111> twinning.
3. The role of dislocations in Gum Metal deformation
Gum Metal generated considerable interest after claims of a dislocation-free deformation mechanism in alloys Ti-12Ta-9Nb-3V-6Zr-O and Ti-23Nb-0.7Ta-2Zr-O (at.%). The authors claimed that these compositions met three molecular orbital parameter requirements. In addition, the alloys were cold-worked to a 90% reduction and contained between 0.7 to 3.0 at.% oxygen. It was claimed that the marble-like microstructure of the alloys formed through the creation of multiple “giant faults” described as macroscopic planar defects carrying very large plastic strains [23]. In addition, no reversible martensitic transformation was reported by the authors to explain the alloys superelastic properties. [4]
The authors proposed that oxygen accumulated around the zirconium to form densely distributed Zr-O clusters which inhibit dislocation motion. As a result, the plastic deformation was to be facilitated via dislocation-free formation of “giant faults” responsible for unique mechanical properties, particularly the ability to sustain very large amounts of plastic deformation. [4]
Deformation in TNTZ alloy Ti-22.6Nb-0.47Ta-1.85Zr-1.34O (at.%) resulted in steps on the surface [REF]. The number of these faults increased with further deformation. The observed steps were similar in morphology to that of “giant faults” [4] and had a “lamellar-like structure composed of parallel {112}<111> nanotwins” [24] containing dispersions of phase. The proposed mechanical twinning deformation process was justified by the need for dislocations to allow for the misorientation between the giant faults. Thus, mechanical twining was the primary deformation mechanism, with dislocations playing a secondary role. [24]
Further claims have been made that the mechanism of deformation in Gum Metal is aided by dislocation activity. In 90% cold-swaged Ti-23Nb-0.7Ta-2Zr-1.2O (at.%) a similar microstructure was reported to be similar to that reported by Saito et al. [4]. Complete crystallisation of the alloy occurred after annealing, in which the cold-swaged fibrous <111> texture was replaced by a new grain structure, one nucleating from deformation bands (“giant faults”), processing random orientations. The recovery process involves the annihilation of dislocations. The deformation bands gradually reduced in size throughout annealing indicating that these regions must contain dislocations, the glide and annihilation of which facilitates the observed recovery process. [25]
Conclusive evidence of dislocation involvement in Gum Metal deformation has been presented by Talling et al. [REF]. Dense dislocation forests were observed via TEM in samples subjected to 45% and 90% cold work. The dislocation density increased throughout deformation, as seen in Figure 3. The reflecting planes of the crystal are thought to have been distorted by the dense dislocation forests making imaging difficult. Furthermore, the peak width of the {321} plane, a well-known b.c.c. slip plane, was seen to broaden via in-situ X-ray diffraction from 0.16% at 0% strain to a maximum of 0.31% at 11.5% strain. Such a broadening can be induced by crystal lattice distortions arising from dislocation activation. [26]

Figure 3. TEM images showing dense dislocation forests in (a) 45% and (b) 90% cold worked Gum metal [26].
4. The reversible stress-induced to ’’ phase transformation
“Martensitic transformations involve the cooperative movement of atoms resulting in a microscopically homogeneous transformation of one crystal lattice into another” [27]. Ti alloyed with sufficient stabilisers undergoes a martensitic transformation from to ’’ as a result of quenching or stress-induced stimuli. The ’’ possesses an orthorhombic lattice in contrast to ’ martensite with a hexagonal lattice. The formation of the ’’ from the is illustrated in Figure 4. Martensitic transformations rely on the cooperative movement of atoms (a diffusionless process), therefore “the formation of the ’’ lattice can be described as a deformation of the lattice” [5] in which two unit cells cooperatively deform to yield an ’’ unit cell of length
2ao, where
aois the austenite lattice parameter. [27]
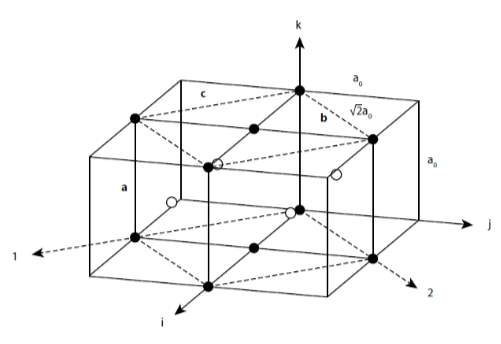
Figure 4. The martensitic transformation of the to ’’’ lattice. The ’’ lattice (dotted lines) is contained within the prior lattice (solid lines). [28]
Superelastic alloys exhibit a reversible stress-induced martensitic transformation. When the stress level reaches the threshold for martensitic transformation, the ’’ phase change occurs. Elastic deformation of the martensitic can then take place. In practice, the martensite phase may deform plasticity when loaded above the yield stress, creating irreversible damage resulting in hysteresis. Upon reduction of the stress level, the initial austenite phase is more thermodynamically stable and upon reaching the retransformation stress, the reverse ’’transformation occurs. [29]
Superelasticity is a temperature-dependent property. The mechanism is a result of a reversible phase transformation between and ’’, which is thermally activated. Consider an alloy initially of 100% martensite phase. As the temperature is increased, the martensite will start to transform to the austenite phase at a given transformation temperature (As) and continue to transform with increasing temperature until the structure is fully transformed to the austenite phase at a temperature Af. Upon reduction of the temperature to the transformation temperature for martensite (Ms), the martensite will begin to grow inside the austenite, until a complete martensite structure has been realised at a further reduced temperature (Mf). This process is seen graphically in Figure 5. [29]
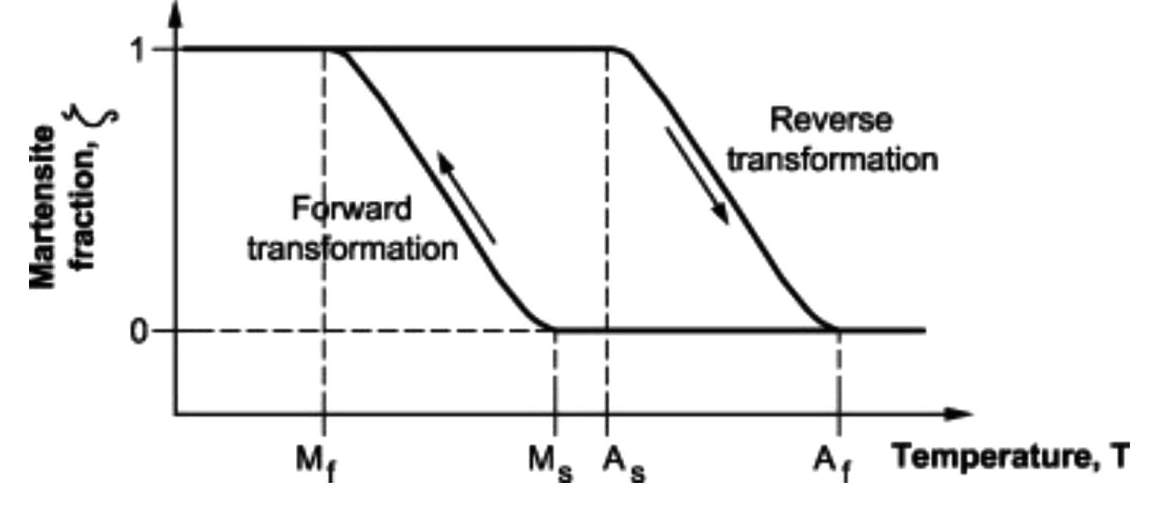
Figure 5. Plot showing the temperature dependence of the reversible martensite transformation [30].
Superelastic effects are exhibited in a narrow temperature range, due to phase stability and the temperature dependence of slip. The temperature of the alloy must initially be above Af as this phase is required to undergo phase transformation. However, the stress needed to initiate the ’’ transformation increases with temperature, whereas the stress required for slip decreases. Creating a critical superelastic region, where the temperature is high enough for Af but low enough for phase transformation to occur preferentially over yielding via slip. This mechanism has been shown to facilitate large superelastic strains of more than 13% [31]. [29]
The martensitic phase ’’ depends on the stability of the phase [32][33][34]. The ’’ is able to form during rapid quenching from the phase provided that the Mo equivalence is below a critical value [33].
Li at el. provide a theoretical model for the creation of SIM in Ti-10V-2Cr-3Al/ Ti-10V-1Fe-3Al (wt.%), with regard to phase stability, expressed through the Mo equivalence. The ‘sweet spot’ for Stress-Induced Martensite (SIM) formation is within a 9-16 Mo wt.% equivalence range. The phase is too stable to deform via a SIM process above 16 Mo wt.%. Below 9 Mo wt.%, thermally-induced martensite will be produced upon quenching, which increases the critical stress for SIM. [35]
The majority of SIM occurs at relativity low levels of deformation. As observed in Ti-10V-2Fe-3Al, SIM forms at 3% strain. The majority of the ’’ forms as thin elongated bands at up to 10% overall strain. At 20% strain, secondary martensite laths form between the primary laths. The formation of the secondary laths coincides with a minor increase in hardness [36].
The grain size affects the fraction of martensite seen in deformed alloys. The volume fraction of martensite in Ti-10V-2Fe-3Al was found to increase for grain sizes between 150m and 250m, but further increases result in a decrease in the ’’ fraction. It was reasonedthat the critical free energy required for the martensitic transformation must therefore initially decrease and then increase with grain size” [36]. Additionally, the critical stress for the ’’ transformation depends on the grain size and stability of the phase i.e. the triggering stress increases with phase stability [37]. The formation of the phase stabilises the phase in some alloys through solute element partitioning, therefore suppressing the martensitic transformation [34].
5. Superelasticity of Gum Metal
Superelastic behaviour displayed by Gum Metal is due to a reversible stress-induced martensitic transformation [38] (Section 4), which can be repeated over the course of numerous cycles. In practice, this phase transformation is not fully reversible due to the formation of crystallographic defects. During cycling, defect accumulation results in a drift of the stress vs. stain hysteresis, where a small amount of plastic stain is incurred with each cycle. This accumulates into an appreciable permeant deformation. The presence of defects also reduces the superelastic transition stress over the course of cycling [39]. It is therefore desirable to produce an alloy that accumulates minimal defects during the transformation. Minimising the volume change between the austenite and martensite phases has been proposed as a possible strategy [5].
In-situ Synchrotron XRD revealed the reversible to ’’ transformation throughout cyclic tensile loading of Gum Metal. The deviation from a linear stress vs. strain behaviour after the first loading cycle was attributed to defects, which formed during the first and subsequent loading cycles. The ’’ scattering peak width increases with the number of load cycles through the stress range implying that dislocation generation accompanies the SIM transformation, which is coherent with other studies [4]. [38]
The exact mechanics of the to ’’ SIM transformation are still unclear. In particular, it is not yet known if there is an association between SIM and the phase. Two possible mechanisms have been proposed regarding ’’ growth from ; either “’’ growth obliterates the or ’’ growth leaves the intact, presumably by nucleating on the interface” [38]. Oxygen was found to retard the to ’’ transformation and increase the shear modulus. This is consistent with other works showing that the addition of oxygen inhibits both the ” formation and deformation twinning [40]. [38]
Over 200 superelastic cycles, Gum Metal experiences a reduction in the Young’s modulus (E) from 65GPa to 55GPa, a drop in the transformation threshold stress from 500MPa to 200MPa, and a drop in the energy dissipated per unit volume after the first cycle. These changes are attributed to permeant mechanical damage in the form of defects, which challenges the reversibility of the to ’’ transformation. Two defect structures are typically found after the SIM transformation. First, the formation of ath (Section 6), which decreases the threshold stress for the phase transformation. The ath may help accommodate the “irrational” ’’interface. The plane of the ’’ interface is misoriented by ~9.4 and ~12.8 from the habit plane of the phase
11̅1̅β. The second defects are dislocations, the number of which increases substantially over 200 cycles. They persist in slip bands that may also contain thin deformation twins. Credited as the likely reason for the hysteresis drift, these dislocations may also nucleate at the ’’ interface. As the ’’ interface plane is approximately 8-10 from the {112} plane, these dislocations may help accommodate the stepped geometry seen in TEM [REF]. Thus, these defect structures are likely to facilitate a lower transformation strain. [39]
Sakaguchi et al. have postulated similar views to Vorontsov et al. [39] in their work on tensile behaviour of Ti-Nb-Ta-Zr alloysto explain the growth of dislocations during cyclic superelasticity. The reduction in the martensitic transformation stress after the first cycle is attributed to the generated dislocations facilitating subsequent SIM by acting as nucleation sites. This offers a convincing argument for the changing stiffness gradients seen in stressvs. strainplots over multiple loading/unloading cycles. [41]
6. The phase
ω is a metastable phase found in metastable Ti alloys. Two types of exist athermal omega (ath) and isothermal omega (iso). The formation of ath and ’’ is believed to be similar, and in some cases, speculated to compete with ’’ formation [REF]. Forming through a diffusionless phase transformation from the by the collapse of alternating <111> planes of the b.c.c. stacking sequence, resulting in B and C planes combining, leaving the A plane unaffected [1]. iso is formed via ageing of a retained microstructure, with a composition of between the and phase fields. Composition, ageing time, and temperature have a strong influence on the volume of iso produced. Whilst there is a consensus that the two types of from via different mechanisms, there is ongoing debate as to whether the iso and ath are two different phases [42]. [43]
The phase results in considerable deterioration of mechanical properties, due to the embrittlement of the With the phase enabling microvoid nucleation and coalescence at low strains [44]. Therefore, great efforts have been made to eliminate its formation during processing. At present, two commercial alloys are used in the aged condition. The vast reduction in mechanical properties is due to embrittlement of the . [43]
6.1. Effect of on twinning
The phase can form via a stress-induced phase transformation, often in parallel with mechanical twinning [45]. At present, the influence of on twinning is yet to be determined, making this topic an important area for future research, particularly with regard to {332}<111> twinning.
The stress-induced athtransformation accompanies {112}<111> twinning in metastable alloys. The nucleation of the phase can occur on the {112} habit plane of the mechanical twins in Ti-23Nb-0.7Ta-2Zr-1.2O (at.%) [45]. The formation of the mechanical {112}<111> twins and the stress-induced has been hypothesised to occur via dislocation motion. In the case of a {112}<111> twin a perfect ½<111> dislocation dissociates into three partial 1/6<111> dislocations forming a three-layered microtwin domain [46][47], and for the phase, a ½<111> dislocation dissociates into two 1/12<111> and a 1/3<111> partial [46][47]. In both cases, the twins and shared a common shear direction <111>{112}. The high prominence of mechanical twinning and transformation was attributed to low stacking fault energy. [45]
The stress-induced athtransformation accompanies {332}<113> twining in a range of metastable-Ti alloys (Ti-Mo, Ti-Nb, Ti-Fe), in which the content of the alloying elements is close to the lower limit for phase retention. Electron diffraction patterns show that for metastable Ti-V and Ti-Mo alloys, when
d0002*/d222*was equal to 0.667, stress-induced athoccurs alongside {332}<113> twinning, with smaller values resulting in reduced formation and little effect on {332}<113> twinning. [48]
6.2. Effect of on superelasticity
The iso phase increases the critical stress for inducing martensite in Ti-Nb alloys, acting to decrease the martensite transformation temperature [49][50]. An unfavourable interaction as if the critical stress for inducing martensite is increased above that for dislocation motion, plastic deformation occurs. The appears as very finely dispersed particles in the matrix, acting to suppress the movement of the martensite interfaces. [49]
The phase ages at low temperatures in Ti-Nb alloys (
~200C). Ageing of the increases its prominence in increasing the critical stress for SIM. This limits the use of formingalloys in high-temperature applications. Alloying additions of Al and Sn have demonstrated effective reduction in aging-in [51]. [49]
7. The influence of oxygen in metastable alloys
Oxygen has a potent effect on suppressing -phase formation. Pinning linear defects and hindering the collapse of {111}required for the to phase transformation. [52]
Large increases in fracture stress of Ti-Nb alloys can be achieved via the addition of oxygen. With oxygen acting as an effective solution hardener, increasing the critical shear stress required for slip [53]. However, the strengthening effect of oxygen in Gum Metal is offset by its potent influence on suppressing the martensitic phase transformation and reducing the recoverable elastic strain. Oxygen stabilises the phase by increasing the shear modulus. Thus, in turn, acts to suppress the martensitic transformation from to ’’. Furthermore, Zr-O clusters have been speculated to hinder dislocation motion [4][8]. However, no conclusive evidence has been published to support this claim. [38]
8. Applications of Gum Metal
Gum Metal processes an attractive combination of material properties: high strength, low elastic modulus, and superelastic behaviour. Desirable properties in a multitude of applications, including construction [54], biomedical implants [55] and sporting goods [56].
The tremendous amount of damage inflicted by natural distastes such as earthquakes and hurricanes is catastrophic and has motivated work to find ‘smarter’ materials with enhanced energy absorbing capabilities that are more resilient. Gum Metal offesr large energy absorption and damping capabilities through its superelastic behaviour.
One potential application of Gum Metal is in earthquake-resistant structural members for buildings. The key advantage of using a superelastic alloy is the ability to recover its original shape and absorb large amounts of energy via superelastic deformation. Gum Metal can be used as braces between structural columns, effectively acting as dampers, Figure 6. [57]
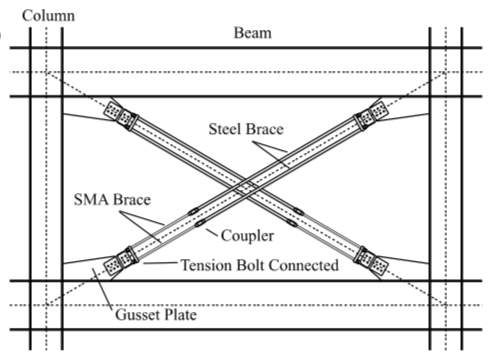
Figure 6. Application of a superelastic alloy brace acting as a cross beam support for building structures [57]
Furthermore, substantial rooftop damage is inflicted on buildings during hurricanes, creating a need for more effective rooftop fasteners. Superelastic alloys have been cited as promising candidates for use as tendons within the fixing, offering a unique adaptability to external vibration. Under low excitation, the tendons act as stiffening devices. Under large excitations, the SIM transformation is initiated, and the tendons act as energy absorption devices due to the unique superelastic deformation mechanism. [58]
Wolff’s law dictates that bone remodels its internal structure and external shape in response to mechanical stress [59]. Thus, it is desirable to produce a prosthesis/implant with mechanical properties closely matching those of bone. The matching of elastic moduli is of key importance. Despite promising research into improving Ti alloys for implantation, such as dual-phase prostheses [2] and novel thermomechanical processing routes [60], the elastic modulus of biomedical implants is still too high,
~114GPa for Ti-6V-4Al [61] compared to 18.6-20.7GPa for bone [62]. Furthermore, the biocompatibility of the current orthopaedic implants is questionable, with fibrous encapsulation of the alloy by the body resulting in failure and revision surgeries after
~40 years.
Gum Metal displays increased bone tissue compatibility and negligible toxicity compared to conventional alloys (Ti-6V-4Al) as seen through in-vitro studies of cell proliferation and focal adhesion formation of pre-osteoblasts. Furthermore, the low elastic modulus of Gum Metal (60GPa) is more favourable when compared to existing alloys with regard to reducing stress shielding. Initial findings provide a strong indication of Gum Metal for use as an orthopaedic prosthesis and remains an exciting area of research. [61]
Superelastic alloys have received growing attention in the aerospace industry for damping applications in turbines. The reversible SIM transformation allows superelastic alloys to be repeatability deformed to high strains and return to their original shape without exhibiting typical fatigue damage. The reversible SIM transformation combined with mechanical twinning of the martensite phase dissipates a large amount of mechanical energy. Thus, it is desirable to incorporate such an alloy into areas of high vibration. Furthermore, hysteresis dampening is independent of vibrational frequency. A key advantage over existing frequency dependant dampening systems which require costly testing to determine the vibrational modes of components. Through tailoring the transformation temperature of the superelastic alloy close to the maximum operating temperature of the component it is to be bonded on, the activation energy required for the phase transition is reduced. Thus, energy dissipation via SIM commences at low vibration levels, preventing vibrations from accumulating to damaging levels.
Research Proposal
The deformation mechanics of Gum Metal are still a highly debated subject, with the nature of twinning, SIM and dislocations interactions yet to be fully determined. This project will verify whether improved superelastic behaviour is possible for the alloy compositions proposed by Luca Montanelli (Table 1). Furthermore, the deformation mechanics the alloys undertake during such behaviour will be assessed throughout the entire loading/unloading cycles, through use of in-situ characterisation techniques. To identify the deformation mechanisms throughout the entire superelastic cycle, and ascertain if the varying stress and crystal structure induces a transition in the dominate deformation mechanism. With particular emphasis on observing {332}<113> twins. To further current understanding on the role of twins in Gum Metal deformation and their evolution throughout the superelastic deformation.
There is lack of in-situ deformation testing of Gum Metal at present, with the majority of the analyses being carried out post-mortem, thus failing to study the deformation mechanisms at various stages in the load cycles. Significant findings have been made due to in-situ testing [16][38][39], highlighting the usefulness of such a technique for viewing deformation in real time. To aid in the previously stated objectives, a custom-built miniature in-situ tensile testing rig, compatible for use within a SEM, will be used in conjunction with larger scale mechanical testing and light microscopy. To yield valuable results regarding Gum Metals deformation mechanisms through superelastic cycling.
A Gantt chart outlining the timeline of the project is given Appendix 1.
9. References
[1] H.K.D.H. Bhadeshia, “Titanium & it’s alloys.” University of Caimbridge, n.d.
[2] Eder S.N. Lopes, Rodrigo J. Contieri, Sergio T. Button, Rubens Caram, “Femoral hip stem prosthesis made of graded elastic modulus metastable beta Ti Alloy,” Mater. Des., vol. 69, pp. 30–36, 2015.
[3] R.R. Boyer, “Titanium for Aerospace: Rationale and Applications,” Adv. Peformance Mater., vol. 2, pp. 349–368, 1995.
[4] T.Saito, T.Furuta, J.H.Hwang, S.Kuramoto, K.Nishino, N.Suzuki, R.Chen, A.Yamada, K.Ito, Y.Seno, T.Nonaka, H.Ikehata, N.Nagasao, C.Iwamoto, Y.Ikuhara, T.Sakuma, “Mulifunctional Alloys Obtained via a Dislocation-Free Plastic Deformation Mechanism,” Science, vol. 300, pp. 464–467, 2003.
[5] Luca Montanelli, “Engineering a titanium alloy displaying stable superelasticity over the course of many cycles,” Imperial Collage London, 2017.
[6] E.S.Fisher, D.Dever, “Relation of the C’ elastic modulous to stability of the B.C.C transition metals,” Acta Metall., vol. 18, pp. 265–269, 1970.
[7] R.J Talling, R.J Dashwood, M. Jackson, D.Dye, “Compositional variability in gum metal,” Scipta Mater., vol. 60, pp. 1000–1003, 2009.
[8] N.Nagasako, R.Asahi, D.Isheim, D.N.Seidman, S.Kuramoto, T.Furuta, “Microscopic study of gum-metal alloys: A role of trace oxygen for the disloaction-free deformation,” Acta Mater., vol. 105, pp. 347–454, 2016.
[9] D.S.Lieberman, M.S.Wechsler, T.A.Read, “Cubic to orthorhombic diffusionless phase change experimental and theoretical studies of AuCd,” J. Appl. Phys., vol. 26, no. 4, pp. 473–484, 1955.
[10] J.S.Bowles, J.K.Mackenzie, “The crystallography of martensite transformations I, II and III,” Acta Mater., vol. 2, pp. 129–137, 1954.
[11] N.N.Greenwood, A.Earnshaw, Chemistry of the elements, 2nd ed. Butterworth-Heinemann, 1997.
[12] H.Y.Kim, J.Fu, H.Tobe, J.I.Kim, S.Miyazaki, “Crystal Structure, Transformation Strain, and Superelastic Property of Ti–Nb–Zr and Ti–Nb–Ta Alloys,” Shape Mem. Superelasticity, vol. 1, no. 2, pp. 107–116, Jun. 2015.
[13] A.W.Sleeswyk, “½<111> screw dislocations and the nucleation of {112}<111> twins in the b.c.c. lattice,” Philos. Mag. J. Theor. Exp. Appl. Phys., vol. 8, no. 93, pp. 1467–1486, 1963.
[14] B.A.Bilby, A.G.Crocker, “The theroy of the crystallography of deformation twinning,” Proc. R. Soc. A, vol. 288, no. 1413, 1965.
[15] Hirobumi Tobe, Hee Young Kim, Tomonri Inamura, Hideki Hosoda, Shuichi Miyazaki, “Origin of {332} twining in metastable beta-Ti alloys,” Acta Mater., vol. 64, pp. 345–355, 2014.
[16] M.J Lai, C.C Tasan, D.Raabe, “On the mechanism of {332} twinning in metastable beta titanium alloys,” Acta Mater., vol. 111, pp. 172–186, 2016.
[17] W.D.Callister, D.G.Rethwisch, Fundamentals of Materials Science and Enginnering: An intergrated spproach, 3rd ed. Hoboken NJ: John Wiley & Sons, 2008.
[18] S.Hanada, O.Izumi, “Deformation of Metastable Beta Ti-15Mo-5Zr Alloy Single Crystal,” Metall. Trans. A, vol. 11A, pp. 1447–1452, 1980.
[19] S.Mahajan, “Interrelationship between slip and twinning in B.C.C. crystals,” Acta Metall., vol. 23, no. 2, pp. 671–684, 1975.
[20] K.P.D.Lagerlöf, “On deformation twinning in b.c.c. metals,” Acta Metall. Mater., vol. 41, no. 7, pp. 2143–2151, 1993.
[21] A.G Crocker, “Twinned martensite,” Acta Mater., vol. 10, no. 2, pp. 113–122, 1962.
[22] T.Kawabataa, S.Kawasakib, O.Izumic, “Mechanical properties of TiNbTa single crystal at cryogenic temperatures,” Acta Mater., vol. 46, no. 8, pp. 2705–2715, 1998.
[23] M.Y.Gutkin, T.Ishizaki, S.Kuramoto, I.A.Ovid’ko, N.V.Skiba, “Gaint faults in deformed Gum Metal,” Int. J. Plast., vol. 24, no. 8, pp. 1333–1359, 2008.
[24] E. Plancher, C.C.Tasan, S.Sandloebes, D.Raabe, “On dislocation involvement in Ti-Nb gu metal plasticity,” Scipta Mater., vol. 68, pp. 805–808, 2013.
[25] W.Y.Guo, X.Hing, J.Sun, X.L.Li, J.S.Wu, R.Chen, “Evolution of Microstructure and Texture during Recrystallization of the Cold-Swaged Ti-Nb-Ta-Zr-O Alloy,” Metall. Trans. A, vol. 39A, pp. 672–678, 2008.
[26] R.J Talling, M.Jackson, R.Dashwood, D.Dye In: M.Ninomi, S.Akiyama, M.Ikeda, M.Hagiwara, K.Maruyuma, “Deformation of Ti-36Nb-2Ta-3Zr-0.3O (Gum Metal),” in Ti-2007 Science and Technology, Sendai, 2007, p. 631.
[27] E.W.Collings, The Physical Metallurgy of Titanium Alloys, vol. 3, 3 vols. United States of America: American Soceity of Metals, 1988.
[28] O.P.J.Joris, “Diffraction Experiments on Superelastic Beta Titanium Alloys,” Imp. Collage Lond., Jul. 2004.
[29] University of Cambridge, “Superelasticity and Shape Memory Alloys,” DoITPoMs, 06-Aug-2009. [Online]. Available: https://www.doitpoms.ac.uk/tlplib/superelasticity/index.php. [Accessed: 30-Dec-2017].
[30] K.Kanayo, E.A.Okotete, “Reconciling viability and cost-effective shape memory alloy options – A review of copper and iron based shape memory metallic systems,” Eng. Sci. Technol. Int. J., vol. 19, no. 3, pp. 1582–1592, Sep. 2016.
[31] Y.Tanaka, Y.Himuro, R.Rainuma, Y.Sutou, T.Omori, K.Ishida, “Ferrous Polycrysalline Shape-Memory Alloy Showing Huge Superelasticity,” Science, vol. 327, no. 5972, pp. 1488–1490, 2010.
[32] Yinong Liu, Hong Tang, “The concern of elasticity in stress-induced martensitic transformation in NiTi,” Mater. Sci. Eng. A, vol. 260, pp. 240–245, 1999.
[33] Han-Sol Kim, Sung-Hwan Lim, In-Dong Yeo, Won-Yong Kim, “Stress-induced martensitic transformation of metastable beta-titanium alloy,” Mater. Sci. Eng. A, vol. 650, pp. 322–325, 2007.
[34] Thierry Grosdidier, Christophe Rouband, “The deformation mechanisms in the beta-metastable beta-CEZ titanium alloy,” Scipta Mater., vol. 36, pp. 21–28, 1997.
[35] C. Li, H. Chen, Z. Wu, W. Wang, “Tuning the stress induced martensitic formation in titanium alloys by alloy design,” J. Mater. Sci., vol. 47, pp. 4093–4100, 2012.
[36] S. Sadeghpur, S.M Abbasi, M. Morakabati, “Deformation-induced martensitic transformation in a new metastable beta titanium alloy,” J. Alloys Compd., vol. 650, pp. 22–29, 2015.
[37] C.Li, X.Wu, J.H.Chen, S, van der Zwaag, “Influance of alpha morphology and volume fraction on the stress-indiced martensitic transformation in Ti-10V-2Fe-3Al,” Mater. Sci. Eng. A, vol. 528, no. 18, pp. 5854–5860, 2011.
[38] R.J Talling, R.J Dashwood, M. Jackson, D.Dye, “On the mechanism of superelasticity in Gum Metal,” Acta Mater., vol. 57, pp. 1188–1198, 2009.
[39] V.A.Vorontsov, N.G.Jones, K.M.Rahman, D.Dye, “Superelastic load cycling of Gum Metal,” Acta Mater., vol. 88, pp. 323–333, 2015.
[40] M.Besse, P.Castany, T.Gloriant, “Mechanisms of deformation in gum metal TNTZ-O and TNTZ titanium alloys: A comparative study on the oxygen influence,” Acta Mater., vol. 59, no. 15, pp. 5982–5988, 2011.
[41] N.Sakaguchi, M.Niinomi, T.Akahori, J.Takeda, H.Toba, “Relationship between tensile deformation behavior and microstructure in Ti-Nb-Ta-Zr system alloys,” Mater. Sci. Eng. C, vol. 25, no. 3, pp. 363–369, 2005.
[42] S.Dubinskly, A.Korotitskiy, S.Prokoshkin, V.Brailovski, “In situ X-ray diffraction study of athermal and isothermal omega-phase crystal lattice in Ti-Nb-based shape memory alloys,” Mater. Lett., vol. 168, pp. 155–157, Apr. 2016.
[43] F.H. Froes, Titanium: Physical Metallurgy, Processing, and Applications. United States of America: ASM international, 2015.
[44] J.C.Williams, B.S.Hickman, H.L.Marcus, “The Effect of Omega Phase on the Mechanical Properties of Titanium Alloys,” Metall. Trans., vol. 2, pp. 1913–1919, Jul. 1971.
[45] H. Xing, J.Sun, “Mechanical twinning and omega transition by #111# [112] shear in metastable beta titanium alloy,” Appl. Phys. Lett., vol. 93, p. 31908, 2008.
[46] L.M.Hsiung, D.H.Lassilia, “Shock-induced deformation twinning and omega transformation in tantalum and tantalum-tungsten alloys,” Acta Mater., vol. 48, no. 20, pp. 4851–4865, 2000.
[47] L.M.Hsiung, D.H.Lassilia, “Shock-Induced Omega Phase in Tantalum,” Scipta Mater., vol. 38, no. 9, p. 13711376, 1998.
[48] S.Hanada, O.Izumi, “Transmission Electron Microscopic Observations of Mechanical Twinning in Metastable Beta Titanium Alloys,” Metall. Trans. A, vol. 17A, pp. 1409–1420, 1986.
[49] H.Y.Kim, Y.Al-Zain, T.Inamura, H.Hosoda, S.Miyazaki, “Effect of Omega Phase on Shape Memory Properties of Ti-base Alloys,” presented at the Proceedings of the 12th World Confernace on Titanium, Beijing, 2011.
[50] H.Kim, S.Miyazaki, “Several Issues in the Devolpment of Ti-Nb-Based Shape Memory Alloys,” Shape Mem. Superelasticity, vol. 2, pp. 380–390, 2016.
[51] P.J.Buenconejo, H.Y.Kim, S.Miyazaki, “Effect of ternary alloying elements on the shape memory behavior of Ti–Ta alloys,” Acta Mater., vol. 57, no. 8, pp. 2509–2515, 2009.
[52] M.Abdel-Hady, K.Hinoshita, M.Morinaga, “General approach to phase stability and elastic properties of beta-type Ti-alloys using electronic parameters,” Scipta Mater., vol. 55, pp. 477–480, 2006.
[53] J.I.Kim, H.Y.Kim, H.Hosoda, S.Miyazaki, “Shape Memory Behavior of Ti-22Nb-(0.5-2.0)O(at.%) Biomedical Alloys,” Mater. Trans., vol. 46, pp. 852–857, 2005.
[54] K.Yamauchi, I.Ohkata, K.Tsuchiva, S.Mivazaki, Shape Memory and Superelastic Alloys: Applications and Technologies. Cambridge: Woodhead Publishing Limited, 2011.
[55] N.B.Morgan, “Medical shape memory alloy applications- the market and its products,” Mater. Sci. Eng. A, vol. 378, no. 1–2, pp. 16–23, 2004.
[56] Kazuaki Nishino, “Super Mulifunctional Alloy ‘GUM METAL,’” RD Rev. Toyota CRDL, vol. 38, no. 3.
[57] H.Tamai, Y.Kitagawa, “Pseudoelastic behavior of shape memory alloy wire and its application to seismic resistance member for building,” Comput. Mater. Sci., vol. 25, pp. 218–227, 2002.
[58] S.Saadat, M.Noori, H.Davoodi, Z.Hou, Y.Suzuki, A.Masuda, “Using NiTi SMA tendons for vibration control of coastal structures,” Smart Mater. Struct., vol. 10, pp. 695–704, 2001.
[59] A.C.Ahn, A.J.Grodzinsky, “Relevance of collagen piezoelectricity to ‘Wolff’s Law’: A critical review,” Med. Eng. Phys., vol. 31, no. 7, pp. 733–741, 2009.
[60] V. Sheremetyev, A. Kudryashova, S. Dubinskiy, S. Galkin, S. Prokoshkin, V. Brailovski, “Structure and functional properties of metastable beta Ti-18Zr-14Nb (at.%) alloy for biomedical applications subjected to radial shear rolling and thermomechanical treatment,” J. Alloys Compd., vol. 737, pp. 678–683, 2018.
[61] D.M.Gordin, R.Ion, C.Vasilescu, S.I.Drob, A.Cimpean, T.Gloriant, “Potentiality of the ‘Gum Metal’ titanium based alloy for biomedical applications,” Mater. Sci. Eng. C, vol. 44, pp. 363–370, 2014.
[62] J.Y.Rho, R.B. Ashman, C.H.Tuner, “Young’s modulus of trabecular and cortical bone material: Ultrasonic and microtensile measurements,” J. Biomech., vol. 26, no. 2, pp. 111–119, 1993.
 Appendix 1. Project Gantt Chart
Appendix 1. Project Gantt Chart
Cite This Work
To export a reference to this article please select a referencing stye below:
Related Services
View allRelated Content
All TagsContent relating to: "Microbiology"
Microbiology is the study of microscopic organisms, or microorganisms. Microorganisms are simple life forms that include bacteria, fungi, algae, and viruses.
Related Articles
DMCA / Removal Request
If you are the original writer of this dissertation and no longer wish to have your work published on the UKDiss.com website then please:




