Optimal Design for Solar Greenhouses Based on Climate Conditions

Abstract

Huge energy consumption in greenhouses is a challenge in developing them to intensify food system while decreasing water consumption in the agriculture sector. Utilizing solar energy in solar greenhouses is a sustainable solution to face this issue. In this study, a solar greenhouse concept considered and a thermal dynamic model developed to predict the inside air temperature. This model integrated to an optimization procedure to find the optimal greenhouse that has the best thermal performance by adjusting its structural parameters. This optimization procedure provides a tool to find the optimal solar greenhouse for each climate condition and predict its performance there. For instance, for the case study of Tehran (Iran), the optimal solar greenhouse works 85% of times passively in year. Besides, this tool is flexible to change the objective function, from year-round performance to seasonal or cultivation period performances, for example, the optimal solar greenhouse for the case study has completely different structural parameters comparing the optimal seasonal solar greenhouse. This is also a decision-making tool to decide the cultivation type based on best energy performance. For the case study, the results indicate that the cultivation of cucumber, melon, and watermelon is the first priority comparing other usual greenhouse products.

Keywords:

Solar Greenhouse, Solar thermal, Heat Transfer Model, Optimization, Solar Energy, Passive Solar, Energy System Modeling

1. Introduction

Three of seventeen goals of the 2030 United Nations sustainable development involve accessing to energy, water, and food and providing security of them [1]. Growing population, urbanization, dietary change, and other consequences of economic development are increasing the demand for energy, food, and water by 30-50% in the next two decades. These are putting pressure on the supply resources and causing environmental damages [2,3]. Energy, water and food are interdependent issues and any strategy focusing on one part of energy-water-food nexus without considering interconnections risks serious unintended consequences [4].

Greenhouse technology is an effective strategy for intensification of food system [5] to meet the increasing demand for food [6] while there are the scarcity of water, energy and land resources [7]. This technology is the junction of energy-water-food nexus by increasing the production yield up to ten times more and decreasing the water consumption up to twelve times less than conventional cultivation, however, energy consumption in them can be up to one hundred times more [8]. Huge energy consumption in greenhouses has been pointed out in many studied for different regions like the Netherlands, Spain, Italy, Turkey, etc. Greenhouses mostly rely on fossil fuels which will lead them to play a significant role in primary energy consumption, pollution, investment and operational costs [9-15] Thus, one of the major technological challenges of greenhouse development is energy consumption [5].

Renewable energy technologies provide access to the secure and environmentally sustainable supply of energy and can be cost-effective as well [16]. From the sustainable development point of view, solar thermal is the most sustainable energy resource [17]. Since the greenhouse itself is a solar collector, utilizing solar energy can lead to a reduction in production cost [18]. Greenhouses can utilize solar energy either through active (using separated collecting systems) or passive (using special structural design to collect solar energy) systems. Solar greenhouses mostly rely on passive solar design but may use active energy systems [5,19] and operate as a semi-passive system. Thus, solar greenhouses can be considered as an effective solution for the energy problem of greenhouses.

Several passive energy systems have been used in greenhouses worldwide including water storage systems, rock bed thermal storages, phase change materials (PCM), thermal screens, north wall (as a heat storage system), and ground air collector for heating, natural ventilation, shading and reflection for cooling, and earth to air exchanger systems for both heating and cooling [20-22]. Since solar greenhouses vary in almost all aspects (shape, style, size, building methods, and technologies), some studies provide the methodologies to choose the correct concept;  for instance zero energy greenhouse concept uses a seven steps procedure and morphological diagram [23,24] and solar greenhouses concept considers seven principles that derive based on best practices [19]. Some studies present innovative designs for solar greenhouses in specific regions based on climate conditions, water resources, and other priorities. “Watergy” greenhouse is a closed greenhouse system works as a solar powered heat exchanger to supply space heating and cooling with lower operation cost while purifies water and use low quality water in climates such as Mediterranean region and temperate central European climate [25]. Seawater greenhouse is another design that works based on solar distillation units and has been developed for arid countries in the Middle East to face the high temperature, water scarcity, and water salinity problems. These concepts were investigated using experimental setups [26] and energy and mass balance models [27]. Chinese solar greenhouses have been developed widely to produce vegetables in the winter without using any auxiliary heating. Using one-sided structure, a thick wall to store heat, night curtain, and common building materials make them total passive greenhouses and easy to develop [28,29]. Cuce et al. comprehensively reviewed renewable and sustainable energy saving measures for greenhouses [30] . The main conclusions of this study were that semi-transparent PV modules can be used as a facade and roof materials in order to control the sunlight input and produce electricity. Seasonal thermal energy storage can also meet the heating demand, and solar assisted heat pump can meet the heating and cooling demand of greenhouses.

Investigating greenhouses performances are done by simulation models and experimental evaluations. The perspective of the studies are different and that determines the accuracy and comprehensiveness of the simulation models. De Zwart developed a comprehensive greenhouse simulation model consist of a heating system model to analysis different methods of heating and energy saving, and a climate simulation model which was capable to predict temperature, CO₂ concentration and humidity of the greenhouse inside air accurately based on energy and mass balance [31,32]. Chen et al. proposed a greenhouse energy demand model based on energy and mass balance and also the biological behavior of the plants, and then optimized environment and energy parameters. The results showed that HPSO-GA (hybrid particle swarm optimization and genetic algorithms) is a more accurate and faster optimization method comparing GA (genetic algorithm) and PSO (particle swarm optimization) methods [33]. A two-dimensional heat transfer model was developed by Cheng et al. to design and predict the temperature of Chinese solar greenhouses based on energy balance equations for heat transfer in system boundaries. Evaluation of this model with experimental data showed that model is capable to predict greenhouse inside air temperature by receiving climate condition (solar radiation, ambient temperature and wind speed), and building material properties [34]. Zhang et al. used computational fluid dynamics (CFD) to simulate the temperature distribution of a solar greenhouse. Investigating the effect of north wall thickness, they employed weighted entropy and fuzzy optimization to achieve the best thickness of the north wall [35]. Deiana et al. considered three scenarios for solar greenhouses and used EnergyPlus simulation tool to optimize energy performance of a greenhouse [36]. Çakir and Şahin compared solar radiation availability in five types of greenhouses structure in order to find optimum size, position and location suitable for cold climates [37]. El-Maghlany et al. used a mathematical model to optimize the design and orientation of an elliptic curve greenhouse for the north tropical region [9].

A wide range of studies covers the energy issue in greenhouses and the concept of solar greenhouses, most of these studies are limited to case studies, special region, and special designs. It is an essential issue that an idea is explained and examined by simulations and experimental prototypes. However, in most cases the lack of a powerful simulation is obvious. Many greenhouse models are either too simple or developed for one specific case. Since solar greenhouses are in fact one type of solar collectors, they are more complex than a common greenhouse. In the previous studies, the focus was on the shape and the equipment of greenhouses while the necessities of a general model to optimize the structural parameters of solar greenhouses which is applicable for any region seems to be neglected. It is possible to do scenario analysis as it was presented on the [36] and [38] studies, but they do not provide the generalize tool to compare different scenarios for regionalization purposes.

The main contributions of this study are to develop an innovative thermal model to predict inside air temperature of a solar greenhouse dynamically (with heat storage capability) by taking input data consisting of climate condition, and to integrate this thermal model to an optimization framework in order to find the optimal design of the greenhouse based on minimization of overheating/overcooling indexes for each climate condition. Figure 1 simply shows the integration of thermal model and optimization framework.

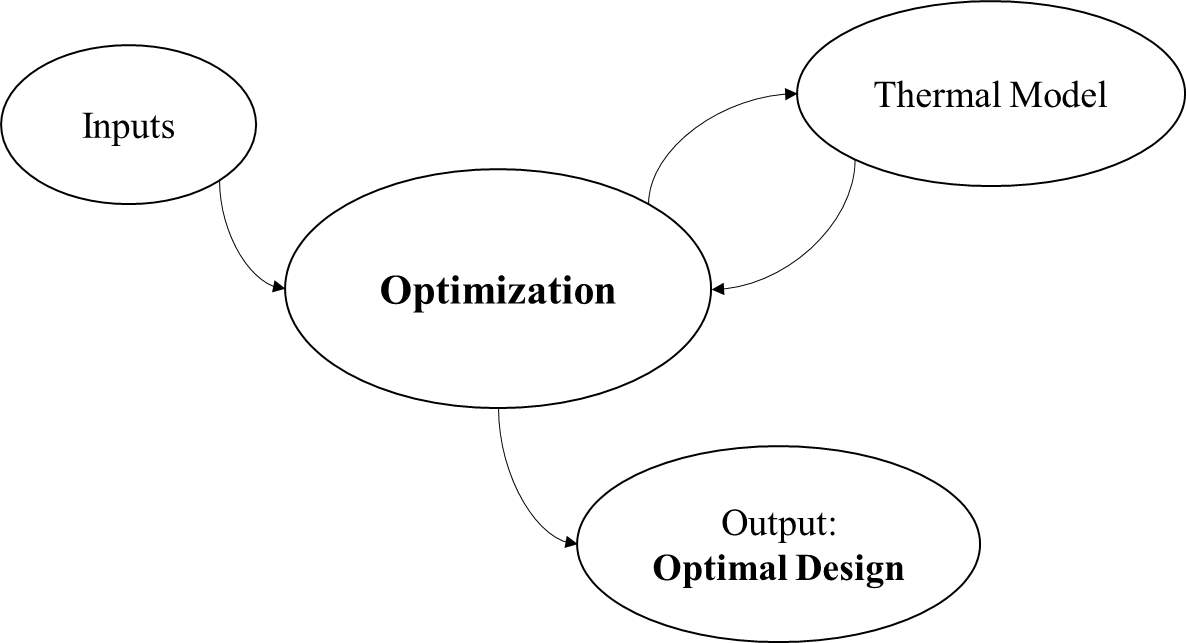
Figure 1: The simplified diagram of the optimization model integrated to the thermal model

2. Modeling

The first step of this study was to consider a solar greenhouse concept. The structure of greenhouse must have a shape that maximizes collecting solar energy and minimizes heat loss. One-sided curved shape greenhouse facing to the south is satisfying since it maximize exposure to light and solar energy (Figure 2). The northern side of the structure has the least contribution in solar energy gain while it causes heat loss, so it is a perfect place to put heat storage system. Heat storage is a thick layered wall consist of one layer of heat storing material, then a layer insulation material and a third layer that complete the insulation. A movable thermal insulation blanket is placed at the roof that covers the transparent cover during the night to prevent the heat loss. Ventilation is done by fans in the eastern and western walls.

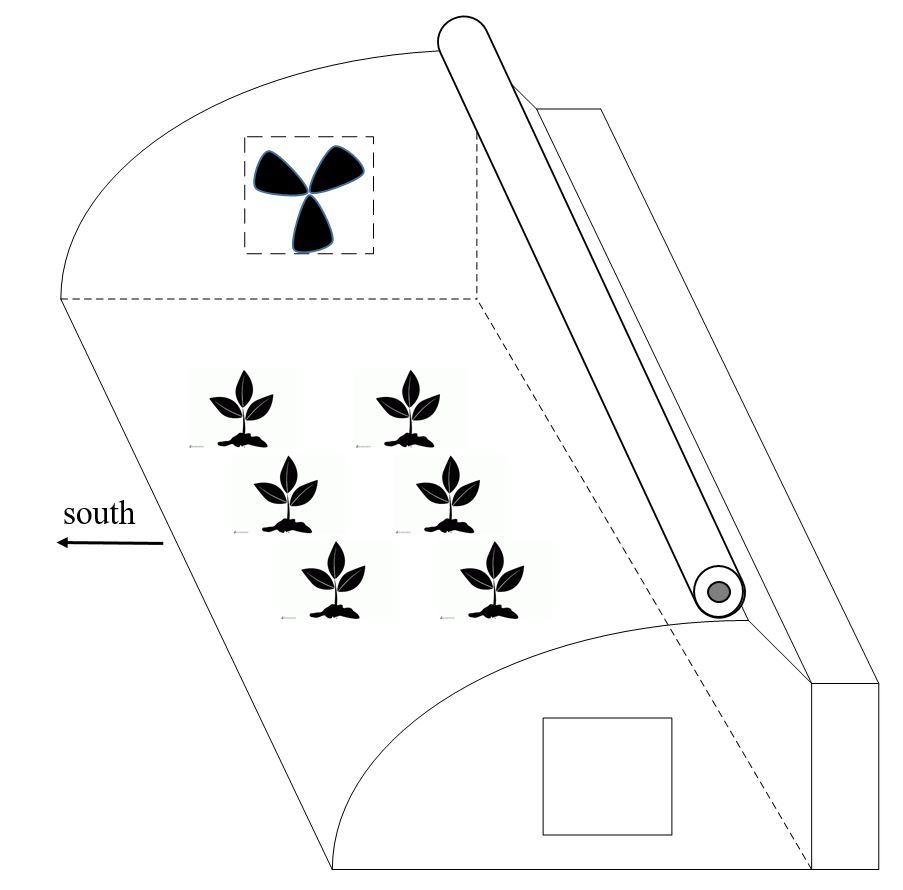
Figure 2: Simple schematic of the solar greenhouse

As it is shown in Figure 3, solar radiation transmits into the greenhouse during the day, the curved shape roof collects solar radiation from sunrise to sunset efficiently. Part of input solar energy is absorbed by heat storage wall and soil of the ground and increases their temperatures (absorbed solar radiation is converted to sensible heat). Temperature difference as the driving force causes heat transfer between the greenhouse surfaces and inside air via convection. Conduction heat transfer happens into the thermal storage wall to store heat in the day and keep the greenhouse warm at night. Part of absorbed solar energy is transformed into the latent heat by crop transpiration and evaporation from wet surfaces. Ventilation is responsible for part of heat loss. Heat loss also happens from the transparent cover of the south roof. To decrease the heat loss at night, a thermal insulation blanket covers the south roof which increases the overall heat transfer coefficient at night.

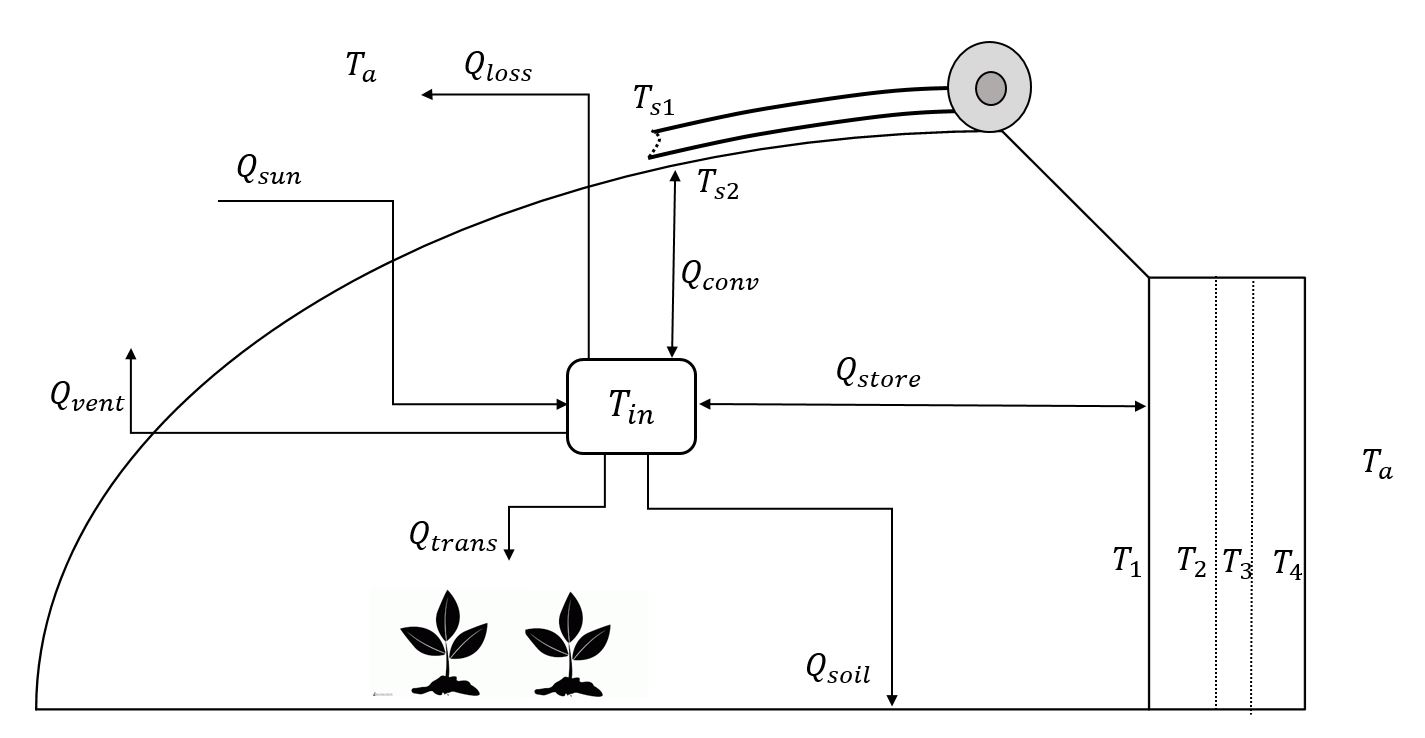
Figure 3: Overview of the climate variable T_in , corresponding energy fluxes and temperatures of different parts of the solar greenhouse

In order to investigate the performance of the solar greenhouse, a dynamic model to predict the greenhouse air temperature is needed. This model should be applicable to different climate conditions, different crops and be able to investigate the effect of changing the construction sizes and materials and also operational parameters like the rate of ventilation. The basis of this model is the greenhouse climate models as described by De Zwart [31], Chen et al. [33], Van Beveren et al. [12] and Trombe wall energy analysis described by Duan et al. [39].

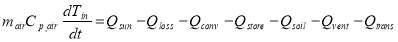
The energy flows in the solar greenhouse is shown in Figure 3. Considering greenhouse inside air as a control volume, the energy balance for this system is elucidated in Eq. 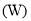1.

                                         (1)

The energy balance for inside air is influenced by input solar insolation , heat loss through transparent cover at day and transparent cover plus thermal insulation cover at night 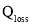, heat transfer via convection between inner side of transparent cover and inside air 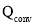, heat transfer via convection between heat storage wall and inside air 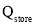, absorbed heat to the ground 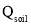, ventilation heat loss 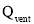(W), and crop transpiration . Also, 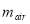(kg) and t (s) represent the mass flux of greenhouse inside air and time, respectively.

Solar insolation adds energy to the inside air and is calculated by Eq. 2, where measured outside radiation (W.m^-2) is multiplied by greenhouse cover transmittance (-) and cover surface area  .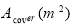

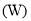                                                                                                       (2)

The main heat loss happens through the transparent cover and it is described by

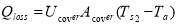      (W)                                                                                     (3)

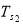Where (W. m^-2.K^-1) is overall heat transfer coefficient which varies in day and night because of using thermal insulation. These parameters are calculated by Eq. 4 for daytime and Eq. 5 for night time. and 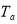(K) is the temperature of the inner side of cover and ambient respectively.

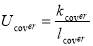          (W. m^-2.K^-1)                                                                                                (4)

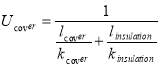        (W. m^-2.K^-1)                                                                                (5)

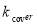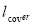In the Eq. 4 and Eq. 5, and (W.m^-1.K^-1) are thermal conductivity of the cover and thermal insulation materials. and 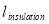(m) are the thickness of the cover and thermal insulation.

Convective heat transfer between the inner side of the transparent cover and inside air is calculated by

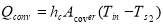        (W)                                                                                      (6)

Where 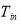(K) is inside air temperature and 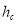(W.m^-2. K^-1) is the convection heat transfer coefficient for inside air. Since in this model it is assumed that ventilation happens using fans it can be concluded that always there is forced convection inside the greenhouse. Considering greenhouse as a non-circular duct, the Nusselt number can be calculated using Colburn equation (Eq. 7) [40], then 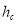is calculated.

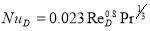                                                                                                         (7)

Convective heat transfer between heat storage wall and inside air is calculated by

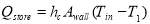       (W)                                                                                          (8)

Where (m²) is the area of heat storage wall and 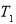(K) is the first layer of heat storage wall temperature.

Some part of input energy is absorbed by the soil (or any other material that covers the floor in case of hydroponic cultivation) and can be calculated by Eq. 9, where 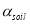(-) is the soil absorptance and 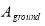(m²) is the floor area.

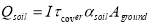         (W)                                                                                      (9)

Ventilation happens in the length of greenhouse and the rate of ventilation is adjusted based on inside air temperature. Eq. 10 illustrate the heat loss caused by ventilation. In this equation, ach is the number of the times that the whole inside air volume changed per time, 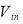(m³) represents the inside volume and 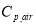(J.Kg^-1.K^-1) is the specific heat of air.

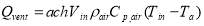         (W)                                                                              (10)

Energy consumption by crop transpiration is described by Eq. 11, based on the Penman-Monteith equation [33][12]:

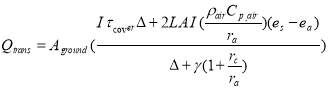           (W)                                          (11)

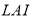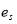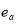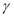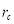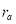Where (Pa.K^-1) is the slop of water vapor saturation curve, is the plant canopy leaf area index, and are saturated vapor pressure of the air (at leaf temperature) and water vapor pressure of the air in Pa, is the psychometric constant of 0.0646 kPa.K^-1, and and are the leaf aerodynamic and stomatal resistance of the leaves of 150 s.m^-1 and 290 s.m^-1, respectively.

In order to predict inside air temperature, it is necessary to realize the temperature of the inner side of the cover (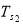) and the first layer of heat storage wall temperature (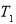) which are the time-dependent parameters. Afterward, they can be put in the Eq. 1 to calculate inside air temperature (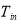) over the time.  Since there is one equation with three variables, it is vital to calculate other temperatures using other equations. Regarding the principles of passive systems modeling [39], energy balances equations are developed for every surface in this greenhouse system. It is assumed the temperature of each surface is uniform and temperature gradient is negligible inside the greenhouse. The heat transfer surfaces are shown in Figure 2, and the energy balance for each one illustrated below as Eqs. 12-29. In energy balance equations all heat transfer mechanism (conduction, convection, and radiation) are considered and equations are written in extended forms.

The first surface is the outer side of the south roof which is transparent cover at daytime and thermal insulation cover at night time and its temperature is shown by 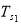. Energy balance for this surface is indicated by Eq. 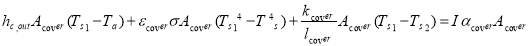12.

      (12)

Where 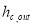(W.m^-2.K^-1) is convective heat transfer coefficient and calculated by Duffie and Bekman equation [41] expresses in Eq. 13, 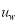(m.s^-1) is wind speed, 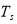(K) is sky temperature calculated by Eq. 14, 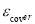is emittance of covering material, and 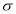(W.m^-2.K^-4) is Stefan-Boltzman constant.

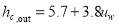                                                                                                             (13)

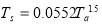                                                                                                                   (14)

Similarly, energy balance for the second surface which is the inner side of the south roof and its temperature is shown by and explained by

(15)

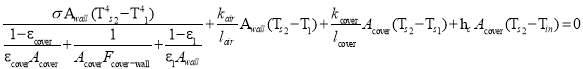
Where is the emittance of the first layer of heat storage wall, 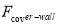is the view factor transparent cover related to heat storage wall, is thermal conductivity of inside air, and 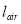is a thickness considered for inside air, which is assumed that equals to the hydraulic diameter of the greenhouse.

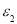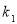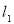The third surface is the internal surface of heat storage wall that its temperature is expressed by Eq. 16, where is the emittance of the second layer of heat storage wall, and are the thermal conductivity and thickness of the first layer of heat storage wall.

(16)

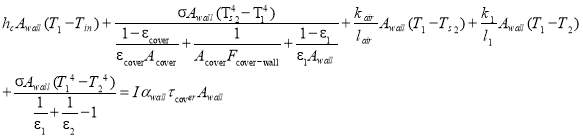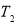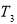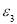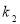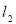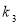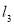The energy balance equation for the surface that connects the first and second layers () and second and third layers () of heat storage wall are explained in Eq. 17 and Eq. 18, respectively. In this equations, is the emittance of the third layer, , , and are the thermal conductivity and thickness of second and third layers of heat storage wall.

                     (17)

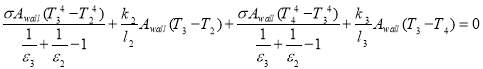                        (18)

Finally, the last one is the outer surface of heat storage wall that 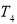is its temperature and the energy balance for this surface explained in Eq. 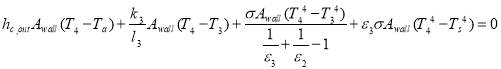19.

               (19)

The above mentioned equations (Eq. 1, 12, 15-19) form a system of non-linear equations. The output of solving them will be the greenhouse inside temperature. It is a dynamic model and calculation is done over the time based on input data. The model can run for a year-round cultivation or for a period of time based on plant cultivation strategy. The data flow diagram is shown in Figure 4, indicating how this model works.

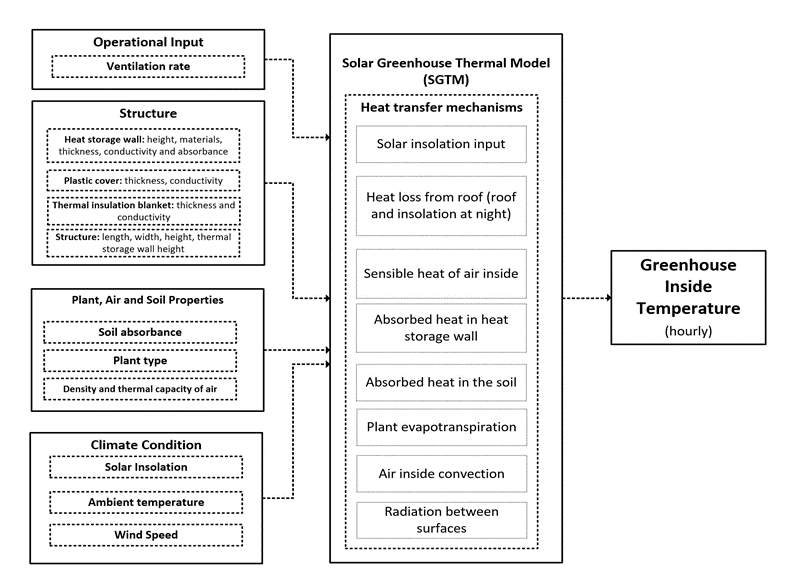
Figure 4: Data flow diagram for thermal model of solar greenhouse 

3. Optimization

The main purpose of a solar greenhouse optimization procedure is the selection of greenhouse structral parameters to achieve the best thermal performance. The objective function can be the minimization of auxiliary energy demand, minimization of energy cost or investment cost, or minimization of temperature deviation from suitable cultivation temperature ranges. In this study, the objective function is to achieve minimum temperature deviation from suitable temperature range because it is the main purpose for planning a greenhouse.

Sine the solar greenhouse has a semi-passive design, the structural parameters play a key role in its thermal performance. Therefore, the decision variables are structural parameters. The considered structural parameters of solar greenhouse system are shown in Figure 5. There are four independent structural parameters that are chosen as the decision variables: 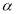and 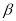angles, width (L) and height (H). It is notable that length (W) assumed long enough to consider the proposed greenhouse as a 2-dimenstional system.

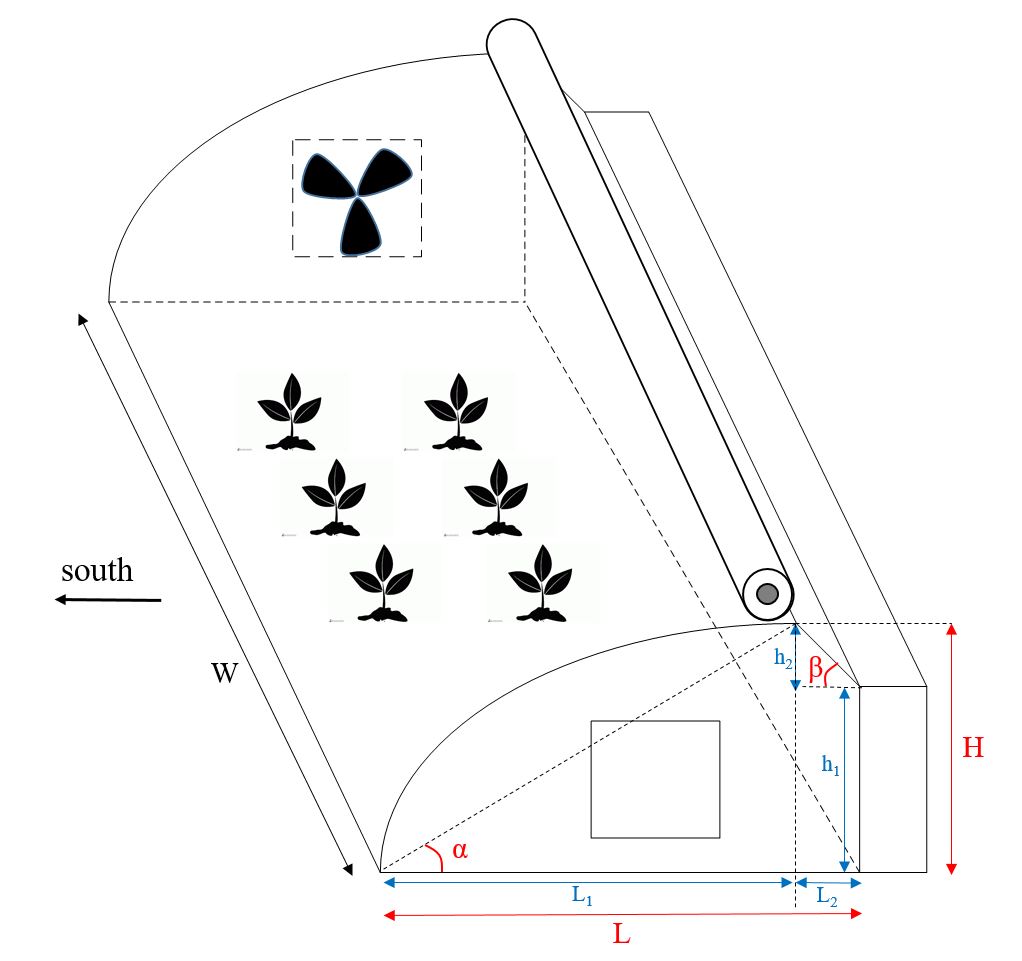
Figure 5: Structural parameters of the greenhouse and the decision variables of the optimization

The deviation from the suitable range of temperature defines as the overcooling index which means deviation from minimum suitable temperature for plants calculated by Eq. 20, and the overheating index which means deviation from maximum suitable temperature for plants is calculated using Eq. 21. Consequently, the objective function is the overall index which is the summation of overcooling and overheating indexes (Eq. 22). 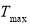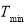and determined based on the type of cultivated plant and varied for day and night.

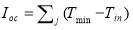
if Tinside>Tmax

(20)

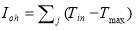
if Tmin>Tinside

(21)

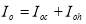                                                                                                                            (22)

Put all together, the optimization objective function and constraints for structural parameters (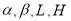), are expressed in Eq. 23. The range that chooses for each constraint is based on the feasibility to construct and the typical ranges [29,35,41]. The first constraint, 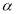cannot be zero because it is not possible to build, and cannot exceed 90 degrees regarding the solar collector principles. The second constraint, 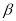which is north roof angle can vary from zero to 90 degree, the bigger 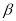gets the more solar insulation inters into the greenhouse. The width (L) and height (H) range are selected based on the typical size of solar greenhouses and the feasibility to construct.

Min Io     =      Min Ioh+Ioc

(23)

Where

10≤α≤90                  (degree)

0≤β≤90                   (degree)

8≤L≤20                             m

3≤H≤15                             m

The iterative method is applied to find the optimal result[43], The optimization procedure is illustrated in Figure 6. Optimization model developed on the thermal model using this algorithm.

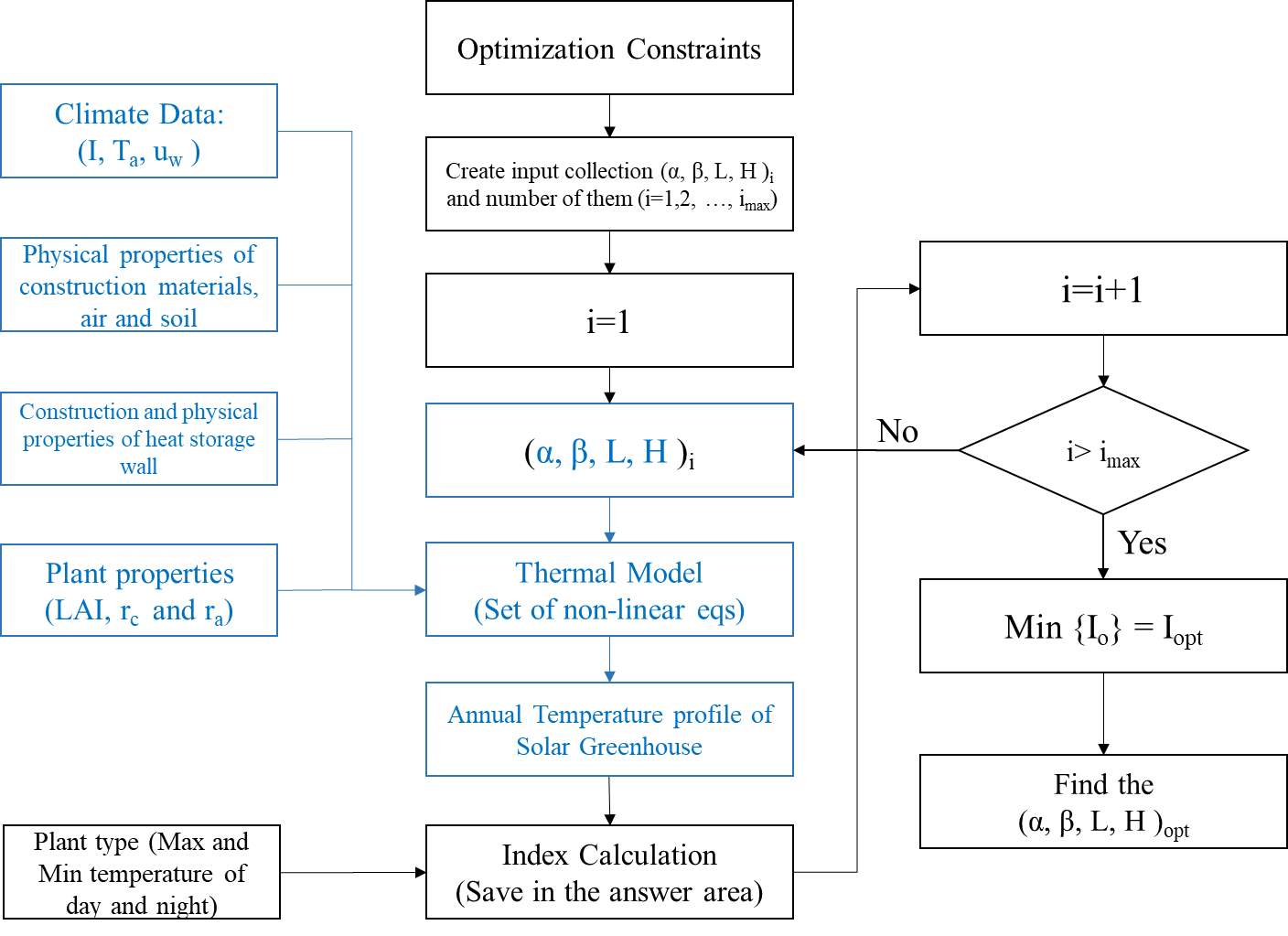
Figure 6: The optimization procedure that indicates the integration of the thermal model (blue boxes) with the optimization model (black boxes) 

4. Results and Discussion 

4.1. Validation

In order to predict reliable results of the thermal model (which is the core of optimization model), the validation process has been done. The best way to check the accuracy of the model results is to compare them with experimental data. Tong et al. studied a similar solar greenhouse located in Shenyang, China (latitude: 41.8⁰N, longitude 123.4⁰E, altitude: 42 m) [44]. The greenhouse was 60 meters long and 12.6 meters wide with a height of 5.5 meters. Also, a 0.6 meter layered heat storage wall made of bricks and XPS foam as a thermal insulation material. The transparent cover was made of 0.12 mm PVC film, covered with a 20 mm thick cotton thermal insulation during the night time. The typical weather file of Shenyang province downloaded from the U.S. Department of Energy [45].

As it is illustrated in Figure 7 the highest temperature difference between this thermal model and experimental data is 2.8 Kelvin and the average of differences is 0.89, which can be considered as an acceptable prediction. The reasons for this deviation can be the following reasons:

• Not specified amount of natural ventilation
• Measurement errors

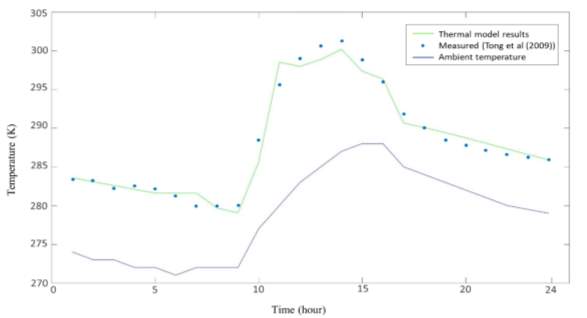
Figure 7: Validation of the thermal model (green line) for hourly greenhouse air inside temperature comparing to experimental data (blue dots) in 20 February 2004 in Shenyang, China [44], blue line represents the ambient temperature

2. Optimization Results

The optimization has done for the case study of Tehran (Iran) climate conditions. Typical weather file for the case study downloaded from the U.S Department of Energy [45]. In this part, the purpose is to find the optimal size of the greenhouse for any climate condition. The natural and physical properties of the structure are explained in Table 1. It also assumed that typical vegetable plants can tolerate the temperature range from 10 to 32 (⁰C) [46] .

Table 1: Natural and physical properties of a typical solar greenhouse structure [36]

Greenhouse Elements	Thickness (m)	Thermal conductivity (W/m.K)	Emissivity ɛ	Absorptance α	Transmission τ
Transparent cover	0.00015	0.17	0.9	0.03	0.88
Thermal insulation	0.036	0.09	0.9	0.75	0
Heat storage wall first layer	0.36	0.81	0.93	0.6	0
Heat storage wall second layer	0.12	0.03	0.9	–	0
Heat storage wall third layer	0.12	0.81	0.93	0.6	0

Figure 8 and Figure 9 indicate the result of the optimization model for the case study. The optimal greenhouse has a height of 11.5 meters and the width of 20 meters. The Alfa and beta angles are 45 and 40 degrees, respectively.  The effect of these angles are on the solar gain, the Alfa angle works as a title angle in other solar systems like solar panels that justifies based on the location, the beta angle effects on the south roof area and determines the amount of solar energy collection as the bigger beta, the more solar energy input. In the optimal greenhouse temperature exceeds 32 degrees of Celsius 390 hours per year, and 900 hours per year is less than 10 degrees of Celsius. Therefore, this greenhouse works 85% of time passively and only in 15% of time needs external heating/cooling (4.5% cooling and 10.5% heating). The annual temperature profile is shown in Figure 10.

The aim of using solar greenhouse is to maximize solar energy utilization and minimize using of active energy systems to provide a desirable micro-climate for plants during the year. The optimal result indicates the optimal greenhouse in year-round cultivation, but sometimes greenhouses work seasonally. In Figure 8 and Figure 9 optimal summer indicates a solar greenhouse that designed to work seasonally just in hot time of year or to work with the least cooling demand in summer, similarly optimal winter indicates a solar greenhouse that designed to work seasonally just in cold time of year or to work with the least heating demand in winter. The optimal summer greenhouse has beta angle of 30 degree and heat storage wall height of 15 centimeters (technically means almost no heat storage system) while the optimal winter greenhouse has beta angle of 60 degrees and heat storage wall height of 65 centimeters which completely explainable because increasing in the beta angle and the height of heat storage wall tie to increasing the capability of solar greenhouse to collect and store more heat.

Figure 8: Result of optimization model including indexes for optimal answer, optimal summer and winter based on hour for the case study in a year

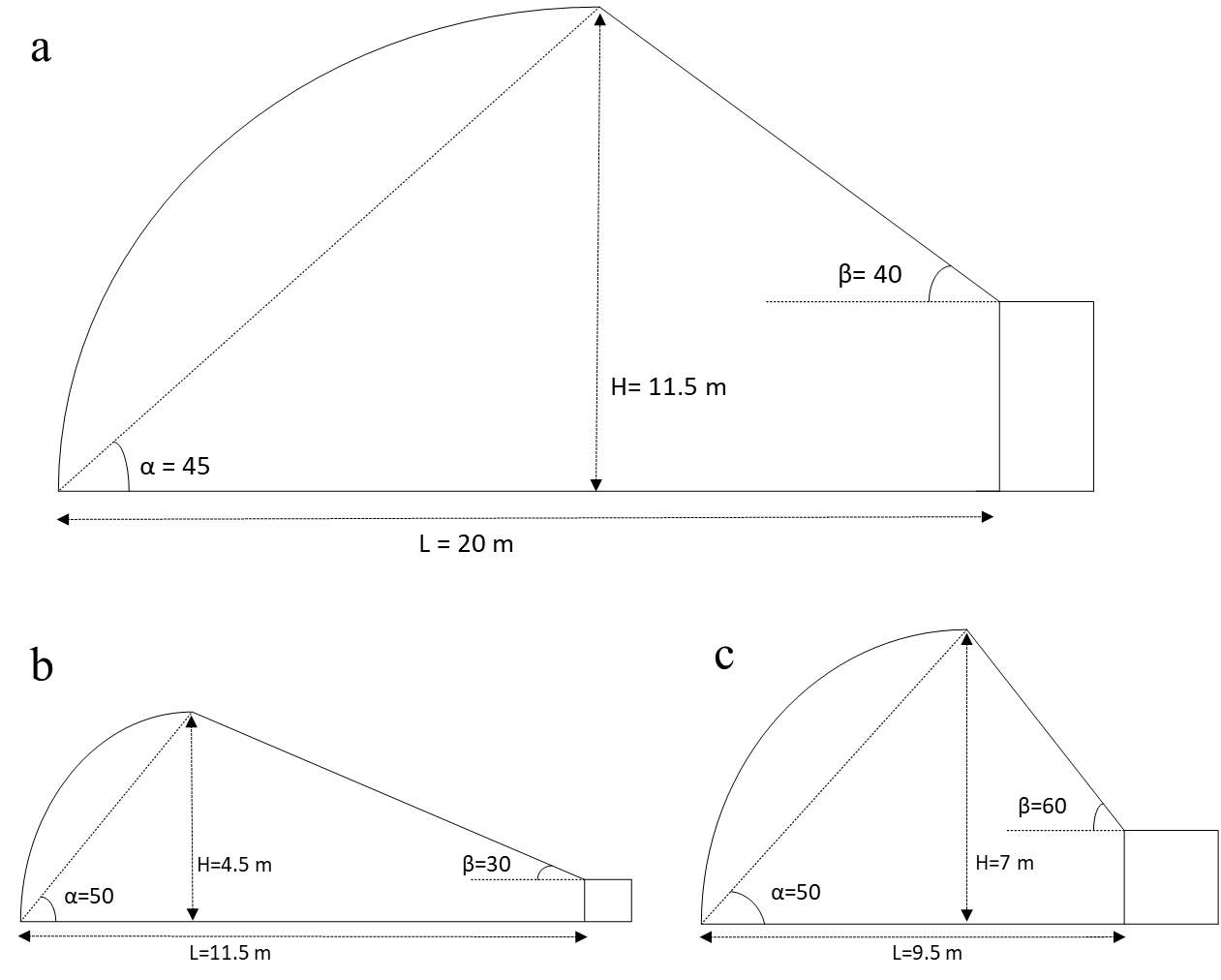
Figure 9: Cross sectional view of optimal greenhouses, a: optimal, b: optimal summer and c: optimal winter for the case study

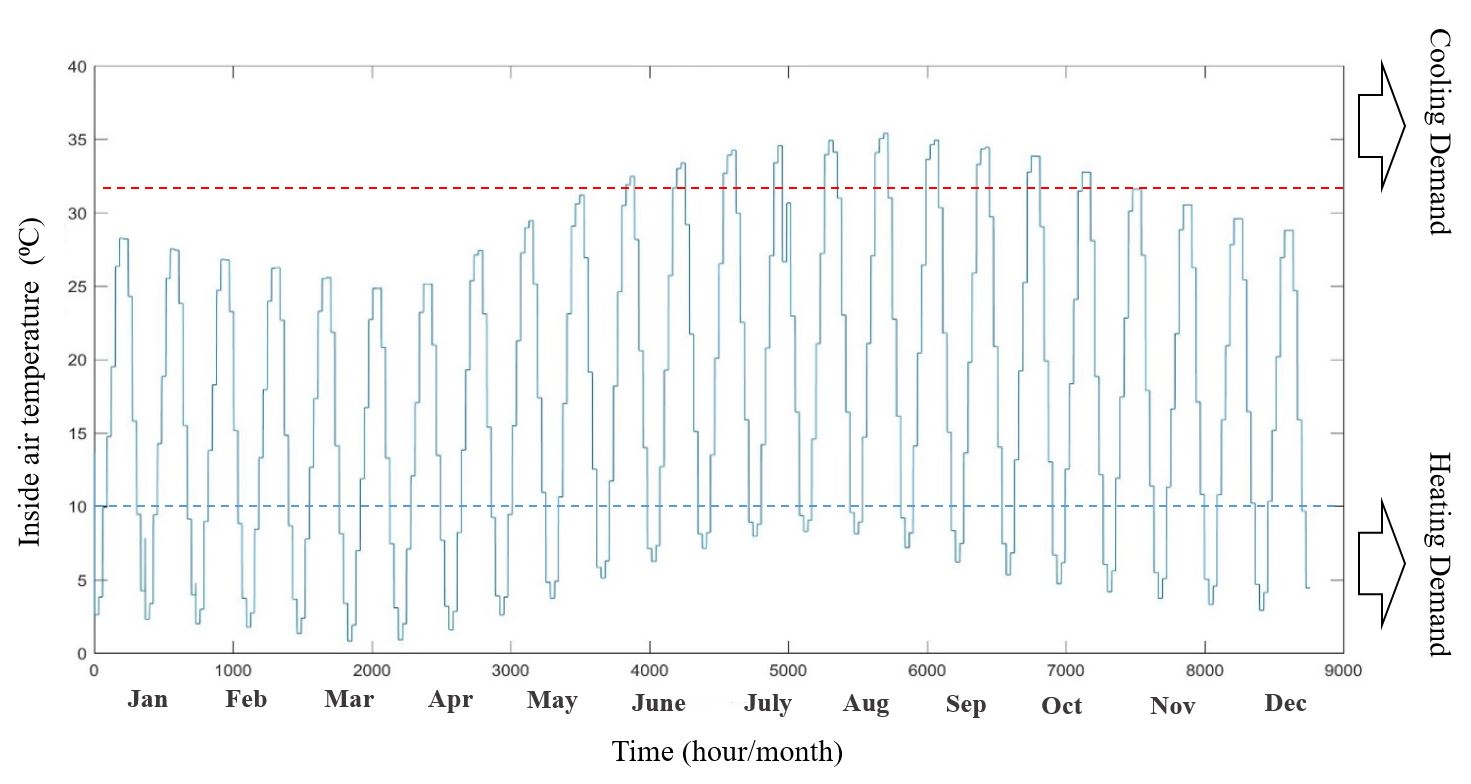
Figure 10: Annual hourly (starting from January) temperature profile for optimal greenhouse, deviation from red dash-line represents cooling demand and from blue dash-line represent heating demand

In the next step, the performance of optimal solar greenhouse is investigated for different crops to realize the priority of cultivation based on thermal performance. The thermal model runs for the optimal greenhouse for each group of crops using the appropriate temperature range of them in day and night (Table 2). The investigation is done for one average day of each month. Table 3 provides a comparison between different crops. So, the priority of cultivation in order to minimize energy demand is:

• Cucumber, melon, and watermelon (54.12% passive)
• Tomato, pepper, and eggplant (53.8% passive)
• Strawberry (50.5% passive)
• Lettuce and cabbage (45% passive)

Based on Figure 13, except some cold months (January, February, and March) that there is heating demand for the whole day, almost in other months greenhouse works well and there is a small deviation from appropriated boundaries. In hot hours of the day in June, July and August there is a small amount of cooling demand that can be achieved by good energy management like shading and ventilation in practice. In fact, the suitable temperature range for the cucumber group includes a wider range comparing to other greenhouse crop groups (Table 2). So the more temperature flexible crop, the best plant to cultivate in the solar greenhouse.

It is notable that this is just based on thermal performance and to make a decision about the type of crop, other parameters like humidity, carbon dioxide, and lightening should be considered. Each crop has its own individual condition of the temperature range, humidity percentage, carbon dioxide concentration and determined illumination in order to grow optimally.

Table 2: Suitable temperature range for greenhouse crops at day and night [46]

Temperature	Day                                          Night
	min	max	min	max
Tomato, pepper, eggplant	19	29	16	20
Strawberry	15	26	13	20
Cucumber, melon, watermelon	20	32	13	23
Lettuce, cabbage	14	22	10	17

Table 3: Summery of the optimal solar greenhouse performance for different crops

Index	Ioh	Ioc	Io	Passive percentage	Thermal performance
Tomato, pepper, eggplant	1214	2827	4041	53.80	Figure 11
Strawberry	2091	2251	4343	50.5	Figure 12
Cucumber, melon, watermelon	1030	2989	4019	54.12	Figure 13
Lettuce, cabbage	3310	1535	4845	45	Figure 14

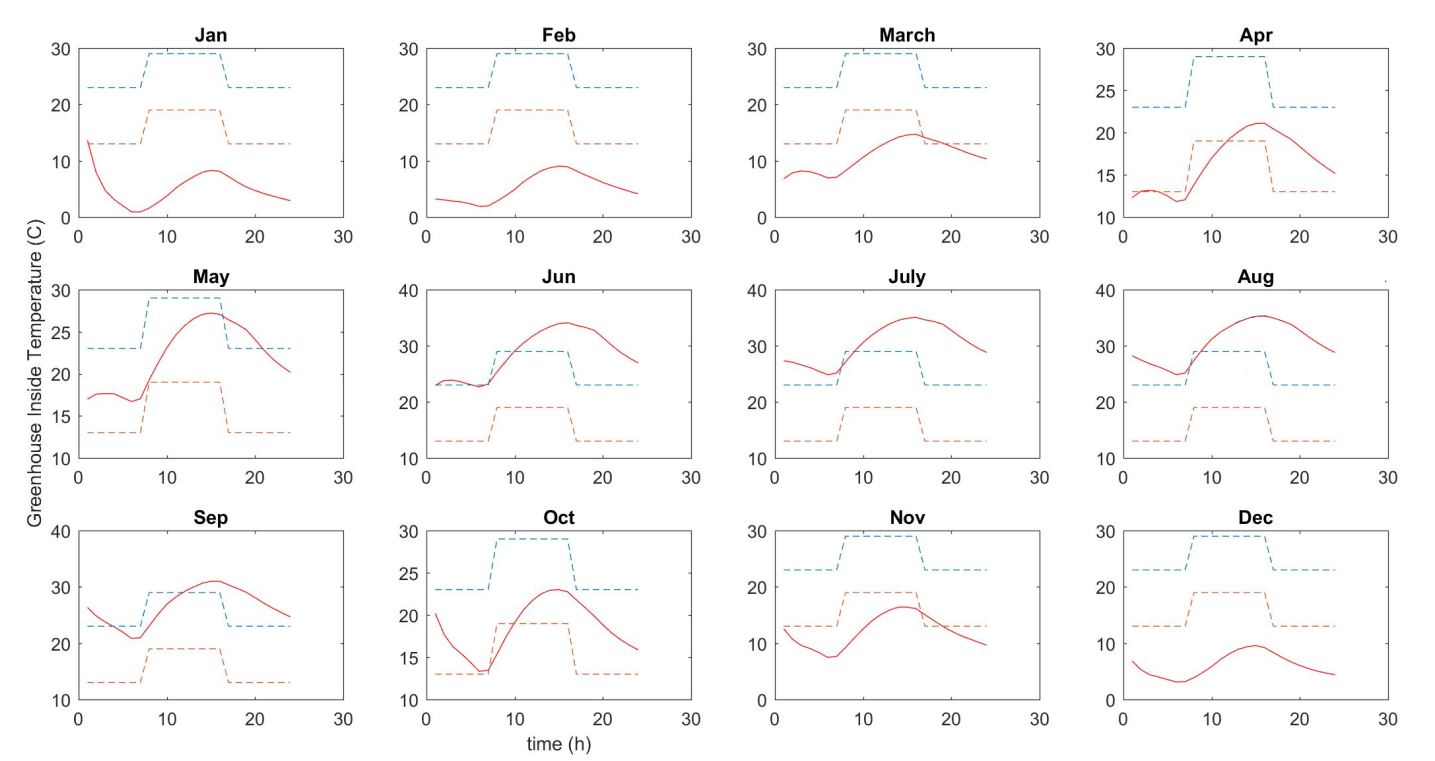
Figure 11: Annual thermal performance of optimal solar greenhouse for tomato, pepper, and eggplant

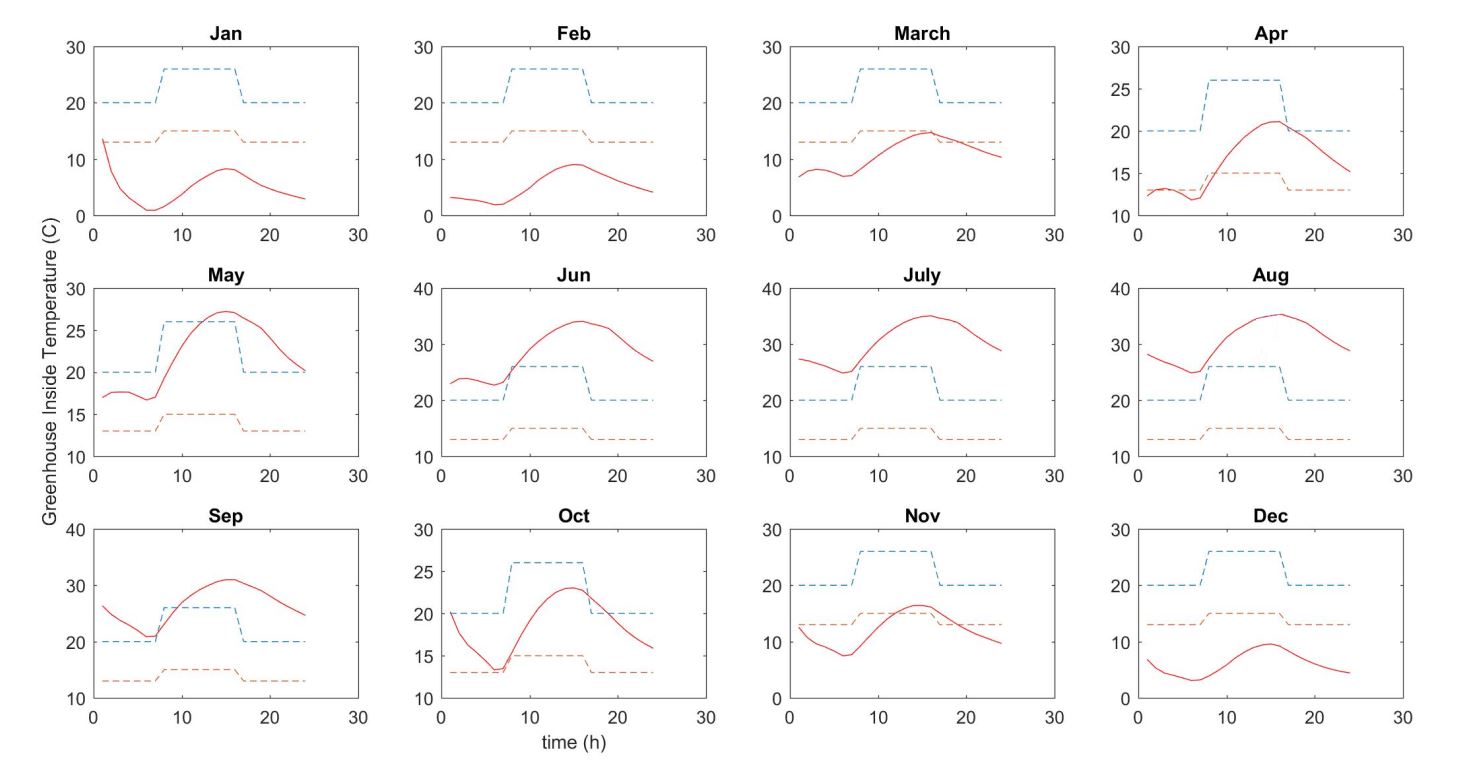
Figure 12: Annual thermal performance of optimal solar greenhouse for strawberry

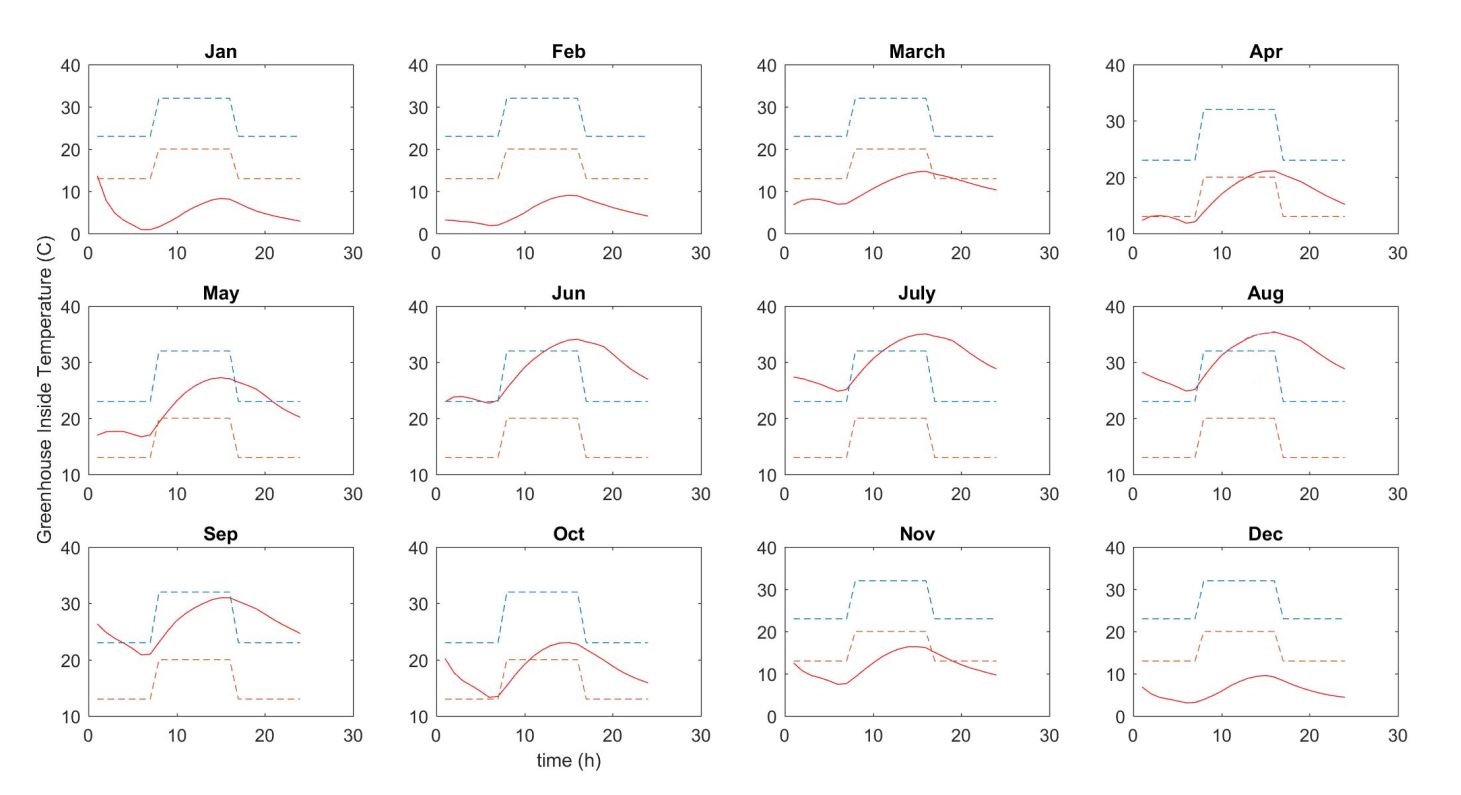
Figure 13: Annual thermal performance of optimal solar greenhouse for cucumber, melon and watermelon

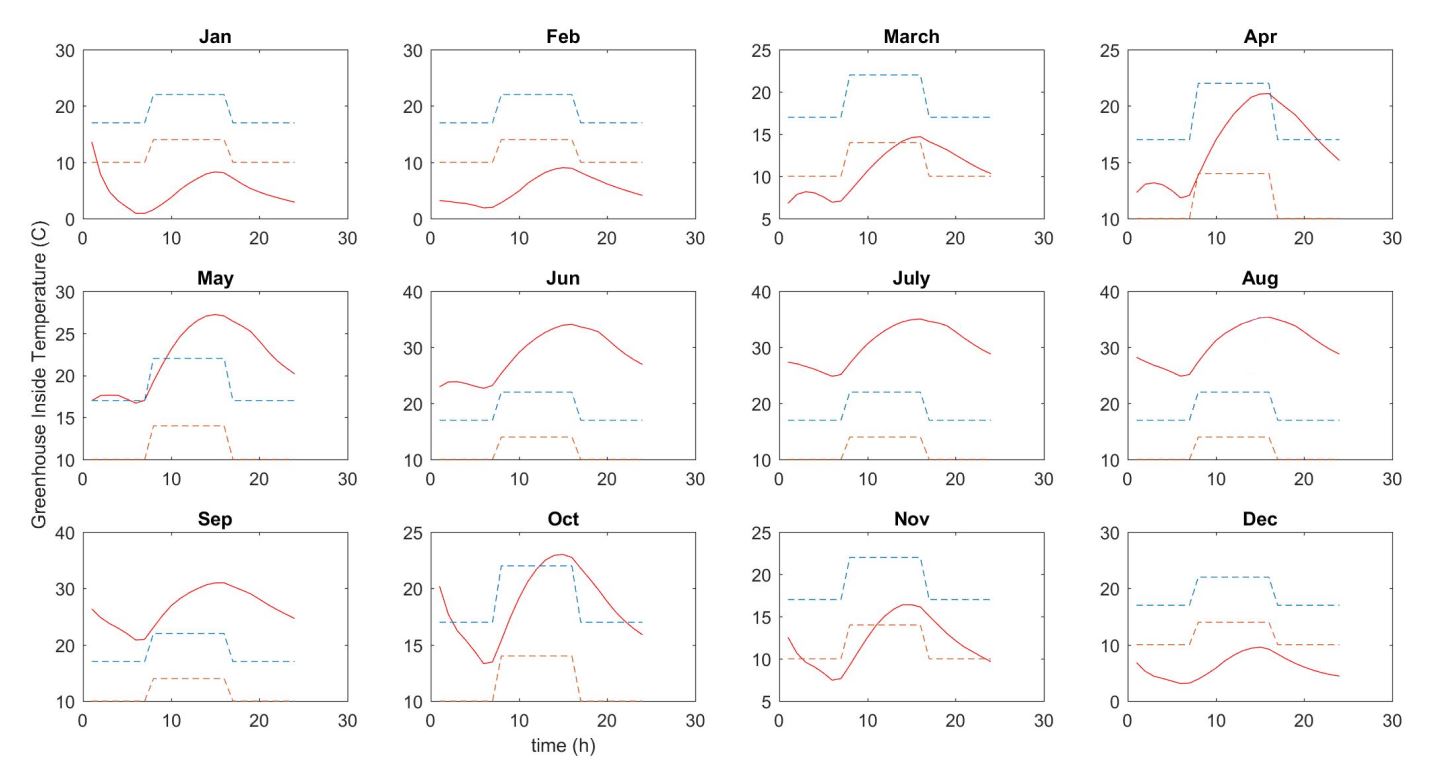
Figure 14: Annual thermal performance of optimal solar greenhouse for lettuce and cabbage 

5. Conclusion

A novel optimization algorithm is developed based on the greenhouse thermal model and evaluated in this study in order to optimize the greenhouse design and report optimal greenhouse performance for each climate condition regarding year-round or seasonal scenarios. Also, this is a decision-making tool to choose the crop type regarding energy demand.

The main findings of this research are:

• Greenhouse technology is an effective strategy to meet the increasing demand for food while there are scarcity resources like water and land. Greenhouses are the junction of water-food-energy nexus since they increase the production yield and energy consumption, and decrease water consumption.
• Solar greenhouse utilizes solar energy as the energy resource and reduce the fossil fuel consumption. This technology produce high yield food while decreases the energy demand as well as water demand.
• In order to achieve the optimum design of solar greenhouse, an optimization procedure were integrated to the heat transfer model. Our findings show that solar greenhouses should be designed regarding the local climate condition. For instance, the optimal solar greenhouse has the passive performance of  85% for the case study. This justified the application of optimization techniques for the optimal design of solar greenhouses.
• The results indicate that solar greenhouse acts as a solar collector and the sizing of it has a great impact on the thermal performance. For the case study, the optimal greenhouse sizing is reported for three scenarios, optimal for the year round, summer and winter and the results demonstrate the whole different sizing for each scenario.
• The later results also indicate that for each location or equally for each climate condition, the optimal greenhouse will have a different sizing.
• The other application of this optimization procedure is to find the cultivation priority based on minimum energy demand. Four group of typical greenhouse products are investigated to be cultivated at the optimal greenhouse of the case study. The priority of cultivation is cucumber, melon and watermelon, then tomato, pepper and eggplant, then strawberry and finally lettuce and cabbage, by having the passive performance of 54.1, 53.8, 50.5 and 45 percent, respectively and the reason is the interaction of the effects of the climate condition and the suitable temperature range of the plant.

References

[1] United Nations General Assembly, “Transforming our world: The 2030 agenda for sustainable development,” https//sustainabledevelopment.un.org/content/documents/7891Transforming%20Our%20World. pdf, no. 1, pp. 1–5, 2015.

[2] A. Irabien and R. C. Darton, “Energy-water-food nexus in the Spanish greenhouse tomato production,” Clean Technol. Environ. Policy, vol. 18, no. 5, pp. 1307–1316, 2016.

[3] L. Bizikova, D. Roy, D. Swanson, H. D. Venema, and M. McCandless, “The Water-Energy-Food Security Nexus : Towards a practical plannig and decision-support framework for landscape investment and risk management,” 2013.

[4] World Economic Forum, M. Companies, and S. R. Company, Global Risks, no. January. 2011.

[5] R. Hassanien, E. Hassanien, M. Li, and W. Dong, “Advanced applications of solar energy in agricultural greenhouses,” Renew. Sustain. Energy Rev., vol. 54, pp. 989–1001, 2016.

[6] I. E. A. (IEA), “World Energy Outlook-2017,” 2017.

[7] M. B. Mesgaran, K. Madani, H. Hashemi, and P. Azadi, “Iran’s Land Suitability for Agriculture,” Sci. Rep., vol. 7, no. 1, pp. 1–12, 2017.

[8] G. L. Barbosa et al., “Comparison of land, water, and energy requirements of lettuce grown using hydroponic vs. Conventional agricultural methods,” International Journal of Environmental Research and Public Health, vol. 12, no. 6. pp. 6879–6891, 2015.

[9] W. M. El-Maghlany, M. A. Teamah, and H. Tanaka, “Optimum design and orientation of the greenhouses for maximum capture of solar energy in North Tropical Region,” Energy Convers. Manag., vol. 105, pp. 1096–1104, 2015.

[10] E. Beshada, Q. Zhang, and R. Boris, “Winter performance of a solar energy greenhouse in southern Manitoba,” 2006.

[11] F. Bronchart, M. De Paepe, J. Dewulf, E. Schrevens, and P. Demeyer, “Thermodynamics of greenhouse systems for the northern latitudes: Analysis, evaluation and prospects for primary energy saving,” J. Environ. Manage., vol. 119, pp. 121–133, 2013.

[12] P. J. M. Van Beveren, J. Bontsema, G. Van Straten, and E. J. Van Henten, “Minimal heating and cooling in a modern rose greenhouse,” Appl. Energy, vol. 137, pp. 97–109, 2015.

[13] J. Reca, C. Torrente, R. López-Luque, and J. Martínez, “Feasibility analysis of a standalone direct pumping photovoltaic system for irrigation in Mediterranean greenhouses,” Renew. Energy, vol. 85, pp. 1143–1154, 2016.

[14] M. Carlini, T. Honorati, and S. Castellucci, “Photovoltaic Greenhouses : Comparison of Optical and Thermal Behaviour for Energy Savings,” vol. 2012, 2012.

[15] M. Esen and T. Yuksel, “Experimental evaluation of using various renewable energy sources for heating a greenhouse,” Energy Build., vol. 65, pp. 340–351, 2013.

[16] R. Ferroukhi et al., “Renewable Energy in the Water , Energy & Food Nexus,” 2015.

[17] J. J. Cartelle Barros, M. Lara Coira, M. P. de la Cruz López, and A. del Caño Gochi, “Assessing the global sustainability of different electricity generation systems,” Energy, vol. 89, pp. 473–489, 2015.

[18] G. K. Ntinas, V. P. Fragos, and C. Nikita-martzopoulou, “Thermal analysis of a hybrid solar energy saving system inside a greenhouse,” Energy Convers. Manag., vol. 81, pp. 428–439, 2014.

[19] L. Schiller and M. Plinke, The Year-Round Solar Greenhouse: How to Design and Build a Net-Zero Energy Greenhouse. 2016.

[20] M. Santamouris, C. A. Balaras, E. Dascalaki, and M. Vallindras, “Passive solar agricultural greenhouses: A worldwide classification and evaluation of technologies and systems used for heating purposes,” Sol. Energy, vol. 53, no. 5, pp. 411–426, 1994.

[21] V. P. Sethi and S. K. Sharma, “Survey and evaluation of heating technologies for worldwide agricultural greenhouse applications,” Sol. Energy, vol. 82, no. 9, pp. 832–859, 2008.

[22] V. P. Sethi and S. K. Sharma, “Survay of cooling technologies for worldwide agricultural greenhouse applications,” Sol. Energy, vol. 81, pp. 1447–1459, 2007.

[23] A. Van’t Ooster, E. J. Van Henten, E. G. O. N. Janssen, G. P. A. Bot, and E. Dekker, “Development of concepts for a zero-fossil-energy greenhouse,” Acta Hortic., vol. 801 PART 1, pp. 725–732, 2008.

[24] A. Vadiee and V. Martin, “Energy management strategies for commercial greenhouses,” Appl. Energy, vol. 114, pp. 880–888, 2014.

[25] G. Zaragoza, M. Buchholz, P. Jochum, and J. Pérez-parra, “Watergy project : Towards a rational use of water in greenhouse agriculture and sustainable architecture,” vol. 211, pp. 296–303, 2007.

[26] A. M. Al-ismaili and H. Jayasuriya, “Seawater greenhouse in Oman : A sustainable technique for freshwater conservation and production,” Renew. Sustain. Energy Rev., vol. 54, pp. 653–664, 2016.

[27] E. Farrell et al., “Reverse electrodialysis powered greenhouse concept for water- and energy-self-sufficient agriculture,” Appl. Energy, vol. 187, pp. 390–409, 2017.

[28] R. Dufault, K. Batal, and D. Decoteau, “Structure, Function, Application and Ecological benefit of a single-slope, energy efficient solar greenhouse in China,” Hort Technol., vol. 1, no. June, 2010.

[29] G. Tong, D. M. Christopher, T. Li, and T. Wang, “Passive solar energy utilization: A review of cross-section building parameter selection for Chinese solar greenhouses,” Renew. Sustain. Energy Rev., vol. 26, pp. 540–548, 2013.

[30] E. Cuce, D. Harjunowibowo, and P. M. Cuce, “Renewable and sustainable energy saving strategies for greenhouse systems: A comprehensive review,” Renew. Sustain. Energy Rev., vol. 64, pp. 34–59, 2016.

[31] H. F. de Zwart, “Analyzing energy-saving options in greenhouse cultivation using a simulation model,” Wageningen University, 1996.

[32] W. Luo, H. Feije de Zwart, J. Dail, X. Wang, C. Stanghellini, and C. Bu, “Simulation of Greenhouse Management in the Subtropics , Part I : Model Validation and Scenario Study for the Winter Season,” Biosyst. Eng., no. March, pp. 307–318, 2005.

[33] J. Chen, J. Zhao, F. Xu, H. Hu, Q. Ai, and J. Yang, “Modeling of energy demand in the greenhouse using PSO-GA hybrid algorithms,” Math. Probl. Eng., vol. 2015, 2015.

[34] M. C.- Wei, H. J.- Jing, and L. Rui, “Research and Development of Simulation and Prediction Software for Thermal Environment of Solar Greenhouse,” China Acad. J., vol. 1001–9, pp. 84–89, 2010.

[35] X. Zhang, H. Wang, Z. Zou, and S. Wang, “CFD and weighted entropy based simulation and optimisation of Chinese Solar Greenhouse temperature distribution,” Biosyst. Eng., vol. 142, pp. 12–26, 2016.

[36] A. Deiana, P. Torino, and I. T. T. To, “Energy performance optimization of typical Chinese solar greenhouses by means of dynamic simulation,” Interanational Conf. Agric. Eng., pp. 6–10, 2014.

[37] U. Çakir and E. Şahin, “Using solar greenhouses in cold climates and evaluating optimum type according to sizing, position and location: A case study,” Comput. Electron. Agric., vol. 117, pp. 245–257, 2015.

[38] H. Esmaeli, “Thermal Model Development for Solar Greenhouse Considering Climate Condition,” Proc. SWC2017/SHC2017, pp. 1–12, 2017.

[39] S. Duan, C. Jing, and Z. Zhao, “Energy and exergy analysis of different Trombe walls,” Energy Build., vol. 126, pp. 517–523, 2016.

[40] T. L. Bergman, F. P. Incropera, and D. P. Dewitt, Fundamental of Heat and Mass Transfer, Seventh. John Wiley and Sons, 2011.

[41] W. H. Mcadams, Heat Transmission, 3 rd. New York: McGraw-Hill, 1994.

[42] G. Tong, D. M. Christopher, and G. Zhang, “New insights on span selection for Chinese solar greenhouses using CFD analyses,” Comput. Electron. Agric., no. 1993, pp. 1–8, 2017.

[43] H. A. Taha, Operations Research: An Introduction, Eighth. New Jersey: Prentice Hall, 1997.

[44] G. Tong, D. M. Christopher, and B. Li, “Numerical modelling of temperature variations in a Chinese solar greenhouse,” Comput. Electron. Agric., vol. 68, no. 1, pp. 129–139, 2009.

[45] “https://energyplus.net/weather, August 11, 2017.” .

[46] FAO, “Good Agricultral Practices for greenhouse vegtable production,” 2013.